| CATEGORII DOCUMENTE |
| Agricultura | Asigurari | Comert | Confectii | Contabilitate | Contracte | Economie |
| Transporturi | Turism | Zootehnie |
REGRESIA LINIARA
1.1 PREZENTAREA MODELULUI
Se considera urmatorul model furnizat de catre teoria economica:
![]()
![]()
Acest model explica fenomenul
economic ![]() in
functie de variabilele explicative
in
functie de variabilele explicative ![]() , in functie de parametrii
, in functie de parametrii ![]() si in
functie de perturbatiile aleatoare
si in
functie de perturbatiile aleatoare ![]() , t =1,,T.
, t =1,,T.
Modelul este numit liniar deoarece
fenomenul economic ![]() este
functie liniara de parametrii
este
functie liniara de parametrii ![]()
Cum se poate observa prin
comparatie cu modelul liniar simplu, acest model integreaza mai multe
variabile explicative (independente). Aceasta multidependenta
liniara va explica mai bine fenomenul economic ![]() , cu toate ca nu vom cunoaste
niciodata exhaustiv ansamblul cauzelor care stau la baza unui fenomen
economic. Partea neexplicata din model este sintetizata,
ca si la modelul liniar simplu, de factorul perturbator (rezidual)
, cu toate ca nu vom cunoaste
niciodata exhaustiv ansamblul cauzelor care stau la baza unui fenomen
economic. Partea neexplicata din model este sintetizata,
ca si la modelul liniar simplu, de factorul perturbator (rezidual) ![]()
1.2 SCRIEREA MATRICEALA A MODELULUI LINIAR MULTIPLU
Se considera un fenomen economic ![]() care depinde
liniar de factorii economici
care depinde
liniar de factorii economici ![]() . Aceasta dependenta se poate scrie
astfel:
. Aceasta dependenta se poate scrie
astfel:
![]() (2)
(2)
Acest model se poate scrie sub forma matriceala in felul urmator:
 (3)
(3)
Pentru a simplifica scrierea se pot folosi urmatoarele notatii:
![]() si
si 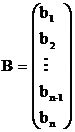
iar modelul (3)
se scrie ![]()
Pentru toate variabile le considerate se vor culege date prin observarea statistica a unui esantion de volum egal cu (T). Schema datelor esantionate poate fi organizata in felul urmator:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()

![]()
Avand in vedere notatia pentru matricea X, aceasta se poate rescrie in felul urmator:
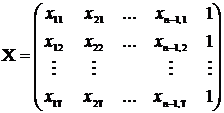
care este o matrice cu (T)-linii si (n)-coloane sau, mai simplu, o matrice de tipul (T,n).
Acum, scrierea matriceala a modelului liniar multiplu (1) se prezinta astfel:
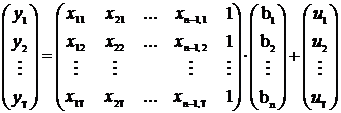
sau simplificat
![]() (4)
(4)
Observatie: Matricea ![]() este de tipul
(T,1);
este de tipul
(T,1); ![]() este o
matrice de tipul (T,n);
este o
matrice de tipul (T,n); ![]() este o
matrice de tipul (n,1);
este o
matrice de tipul (n,1); ![]() este o
matrice de tiplul (T,1).
este o
matrice de tiplul (T,1).
Daca se tine cont in cadrul scrierii matriceale de momentul la care se face observatia, atunci din (4) se obtine
![]()
![]() (5)
(5)
unde matricea ![]() este o
matrice de tipul (1,n) si are forma
este o
matrice de tipul (1,n) si are forma
![]()
![]()
IPOTEZE CLASICE ASUPRA MODELULUI
(h1) Matricea ![]() a
variabileleor explicative este o matrice sigura, adica observata
fara erori. Realizarea acestei ipoteze conduce la obtinerea
estimatorilor nedeplasati.
a
variabileleor explicative este o matrice sigura, adica observata
fara erori. Realizarea acestei ipoteze conduce la obtinerea
estimatorilor nedeplasati.
(h2) Speranta matematica a erorilor care afecteaza modelul este zero, sau altfel spus, modelul liniar multiplu este in medie bine specificat.
![]()
![]()
(h3) Erorile (perturbatiile) sunt necorelate, adica covarianta intre oricare doua perturbatii diferite este nula.
![]()
(h4) Erorile (perturbatiile) sunt homoscedastice, adica varianta perturbatiilor este
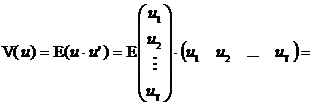
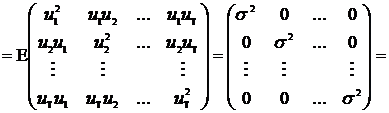
![]() .
.
(h5) Erorile si variabilele explicative sunt necorelate intre ele, adica covarianta intre erori si variabilele explicative este zero.
![]()
(h6) Erorile
modelului sunt normal si identic distribuite, adica ![]()
(h7) Exista
matricea ![]() sau
sau ![]()
(h8) ![]() matrice finita, nesingulara.
matrice finita, nesingulara.
(h9) ![]() , adica numarul de observatii este
cel putin egal cu numarul de variabile aduse in model.
, adica numarul de observatii este
cel putin egal cu numarul de variabile aduse in model.
1.4.ESTIMAREA PARAMETRILOR DIN MODEL PRIN METODA PMO
Se considera modelul liniar multiplu scris sub forma matriciala:
![]()
Se propune
determinarea unei estimari a vectorului ![]() . Se noteaza acest vector al estimatorilor cu
. Se noteaza acest vector al estimatorilor cu ![]() , unde
, unde

Se va folosi metoda celor mai mici patrate minime ordinare (PMO), adica se doreste minimizarea urmatoarei sume:
![]()
In urma aplicarii metodei (PMO) se obtine pentru vectorul estimatorilor urmatorul rezultat:
![]() (1.1)
(1.1)
Observatie: Matricea
(vector) ![]() este de tipul
(n,1); matricea
este de tipul
(n,1); matricea ![]() este de tipul
(n,T) si reprezinta matricea
transpusa a matricii
este de tipul
(n,T) si reprezinta matricea
transpusa a matricii ![]() (T,n); matricea ( vector)
(T,n); matricea ( vector) ![]() este de tipul
(T,1) .
este de tipul
(T,1) .
Odata determinat vectorul
estimaorilor (![]() ) se pot calcula valorile ajustate ale vectorului
) se pot calcula valorile ajustate ale vectorului ![]() dupa
urmatoarea relatie:
dupa
urmatoarea relatie:
![]() (1.2)
(1.2)
iar vectorul
erorilor estimate (numit inca si vectorul rezidurilor) se va putea
calcula ca si diferenta dintre vectorul ![]() si
si ![]() , adica
, adica
![]() (1.3)
(1.3)
sau
![]() , t = 1,,T (1.4)
, t = 1,,T (1.4)
Ecuatia de analiza a variantei
Se poate
observa, din scrierea (1) a modelului liniar multiplu, ca acesta cuprinde
si o constanta, notata ![]() Aceasta constanta are un rol important in cadrul modelului,
prezenta ei face ca media erorilor estimate sa fie egala cu
zero.
Aceasta constanta are un rol important in cadrul modelului,
prezenta ei face ca media erorilor estimate sa fie egala cu
zero.
Asadar, se poate scrie
![]() (1.5).
(1.5).
Deasemenea, se
stie ca ![]() , t = 1,,T. Atunci se poate scrie:
, t = 1,,T. Atunci se poate scrie:
dar avand in vedere relatia (3.5) se obtine
![]() (1.6)
(1.6)
Relatia (1.6) demonstreaza ca modelul estimat trece exact prin punctul mediu al esantionului, adica
![]() (1.7)
(1.7)
Acest ultim rezultat permite scrierea ecuatiei de analiza a variantei
![]() (1.8)
(1.8)
varianta lui ![]() = varianta explicata de model +
varianta perturbatiilor
= varianta explicata de model +
varianta perturbatiilor
Pentru termenii ecuatiei de analiza a variantei (1.8) se vor folosi urmatoarele notatii:
![]() - suma patratelor totale
- suma patratelor totale
![]() - suma patratelor estimate
- suma patratelor estimate
![]() - suma patratelor reziduale
- suma patratelor reziduale
Ecuatia
(1.8) se rescrie: ![]()
1.6 Coeficientul de determinatie R2
Folosind ecuatia (1.8) se va determina coeficientul de
determinatie ![]() care reprezinta un indicator de eficienta
al modelului liniar multiplu.
care reprezinta un indicator de eficienta
al modelului liniar multiplu.
Se obtine:
![]() (1.9)
(1.9)
de unde
![]() (1.10)
(1.10)
Valorile lui ![]() sunt cuprinse
in intervalul
sunt cuprinse
in intervalul ![]() Cu cat
valoarea lui
Cu cat
valoarea lui ![]() este mai apropiata de 1 cu atat se poate afirma
ca modelul ales este mai eficient, adica estimatiile
obtinute prin model se apropie mai mult de valorile reale.
este mai apropiata de 1 cu atat se poate afirma
ca modelul ales este mai eficient, adica estimatiile
obtinute prin model se apropie mai mult de valorile reale.
Previziunea variabilei explicate (y)
Se considera modelul liniar multiplu in forma (5)
![]()
![]()
Se propune rezolvarea urmatoarei probleme: pentru o valoare oarecare, (![]() ), a
vectorului
), a
vectorului ![]() , ce
valoare ar putea lua variabila explicata
, ce
valoare ar putea lua variabila explicata ![]()
Exista asadar valoarea
![]()
O valoare posibila a
marimii (![]() ), numita si predictia lui (
), numita si predictia lui (![]() ), este oferita de modelul estimat
), este oferita de modelul estimat
![]() (1.11)
(1.11)
Pentru a putea aprecia
corectitudinea predictiei, (![]() ), trebuie analizata eroarea de previziune. Aceasta
se definiste in felul urmator:
), trebuie analizata eroarea de previziune. Aceasta
se definiste in felul urmator:
![]() . (1.12)
. (1.12)
Eroarea de previziune, (![]() ), este o
variabila aleatoare. Are sens, deci, trebuie calculate
valorile
), este o
variabila aleatoare. Are sens, deci, trebuie calculate
valorile ![]()
Aceste valori se obtin prin relatiile:
![]()
![]()
Avand in
vedere observatia de mai sus se impune estimarea marimii (![]() ), care se
obtine cu relatia:
), care se
obtine cu relatia:
![]() (1.13)
(1.13)
Atunci cand se
face previziunea unei variabile este util sa se determine si
intervalul de incredere pentru valoarea previzionata (![]() ). Intervalul
de previziune are forma:
). Intervalul
de previziune are forma:
![]() , (1.14)
, (1.14)
unde ![]() , reprezinta valoarea tabelara a legii student,
citita pentru pragul de semnificatie (
, reprezinta valoarea tabelara a legii student,
citita pentru pragul de semnificatie (![]() ) si numarul gradelor de libertate (
) si numarul gradelor de libertate (![]() ) .
) .
Florea I., Parpucea I., Buiga A., "Statistica descriptiva. Teorie si aplicatii", Editura Continental, Alba Iulia, 1998, p. 97;
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 2279
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2025 . All rights reserved