| CATEGORII DOCUMENTE |
| Agricultura | Asigurari | Comert | Confectii | Contabilitate | Contracte | Economie |
| Transporturi | Turism | Zootehnie |
Teoria Localizarii
Abordarea moderna a problematicii spatiale in economie a inceput cu lucrarea lui Johann Heinrich von Thnen, din anul 1826, Der isolierte Staat in Beziehung auf Landwirtschaft und Nationalkonomie (Statul izolat in raport cu spatiul economic si economia nationala) .
Modelul lui von Thnen
Acest model isi propune sa gasesca o localizare optima a culturilor agricole in functie de distanta dintre locul de productie si pietele de desfacere.
Ipotezele modelului sunt:
- terenul de cultura a plantelor este un plan uniform, de fertilitate constanta;
- izolarea terenului de cultura de catre un desert, sau o alta suprafata arida;
- facilitatile de transport sunt asemanatoare in toate directiile, rezultand inexistenta cheltuielilor de transport in procesul de productie, ci numai in cel de distributie;
- piata de desfacere este reprezentata de un oras si devine punctiforma in analiza.
In acest mod, optimizarea modelului se va face in functie de renta funciara.
Treptat, von Thnen va complica modelul introducand diferite discontinuitati in spatiul initial izotrop (de exemplu un rau navigabil), pentru a se apropia mai mult de spatiul real.
Varianta cea mai cunoscuta a modelului considera sase culturi agricole (x, y, z, u, v, w), pentru care renta funciara scade proportional cu distanta dintre locul de productie si piata de desfacere, conform dreptelor Aa, Bb,, Ff de panta negativa (fig. 2.5). Dreptele sunt trasate intr-un sistem de axe rectangulare, unde pe abscisa este repezentata distanta, iar pe ordonata este reprezentat venitul obtinut de pe urma culturii respective (renta funciara) in functie de distanta. Se considera urmatoarele puncte de intersectie intre perechile de drepte astfel: P pentru dreptele Ff si Ee, Q pentru Ee si Dd,, T pentru Bb si Aa. Considerand un comportament de maximizare a veniturilor, frontiera de venituri maxime va fi data de urmatoarele segmente: FP, PQ, QR, RS, ST si Ta, fiecare segment corespunzand unei anumite culturi agricole. Proiectiile acestor puncte pe abscisa vor delimita razele cercurilor corespunzatoare fiecarei culturi. Se obtine in final o structurare a terenului agricol pe inele concentrice (1, 2,,6), numite uneori inelele lui von Thnen. Structura obtinuta este asemanatoare celei preconizate de James Stuart in cazul culturilor din jurul unui oras, numai ca de asta data avem o fundamentare stiintifica a localizarii culturilor agricole.
unde avem urmatoarea corspondenta: cultura
renta funciara x Aa y Bb z Cc u Dd v Ee w Ff
![]()
![]()
![]()
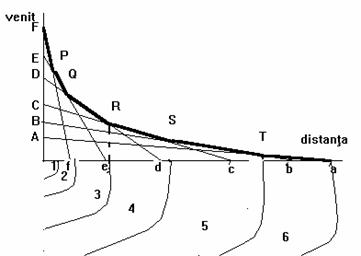
Figura 2.5. Localizarea culturilor agricole conform modelului lui von Thnen.
Zonele de cultura se repartizeaza astfel: Zona 1 va fi atribuita culturii pentru care portiunea din dreapta rentei funciare este cea mai inalta, respectiv w, deoarece FP depaseste toate celelalte drepte. Dupa punctul P, renta corespunzatoare acestei culturi (dreapta Ff) va fi mai mica decat aceea corespunzatoare culturii a carei renta funciara este Ee (v) si anume, segmentul PQ devine cel mai mare. Prin urmare, cultura v va inlocui cultura w. Mai departe, intrucat segmentul QR din dreapta Dd depaseste dreapta Ee, cultura u va inlocui cultura v, fiindu-i atribuita zona 3, s.a.m.d. Se fundamenteaza, astfel, pe o baza stiintifica (bazata pe matematica) modul de distribuire spatiala a culturilor agricole. Totodata von dezvolta teoria rentei (Ricardo) introducand in analiza conceptul de distanta (figura 2.2)
a) Ricardo b) von Thnen
![]()
![]() P P
P P
Renta


![]()
![]()
![]()
![]() P* P0
P* P0
Renta
Cost transport
Cost productie
Cost productie
![]()
![]()
![]()
Fertilitate descrescatoare F0 Zona de productie distanta piata
Fig. 2.2 Comparatia rentei la Ricardo cu renta la von Thnen
Se observa ca in timp ce la Ricardo, renta deriva doar din fertilitatea solului, fiind data de diferenta dintre pretul pietei si costul de productie (fig. 2.2. a)), la von Thnen, renta este diferenta dintre pret si suma costului de productie cu cel de transport (fig. 2.2. b)).
Localizarea unitatilor de productie industriala. Modelul lui Weber.
Aplicarea principiului orientarii productiei catre piata se aplica si in cazul unitatilor industriale. Exista totusi o diferenta importanta: daca productia agricola determina zonarea terenurilor (a unor arii in spatiu), in cazul productie industriale vom avea de-a face cu fixarea unor puncte in spatiu . Astfel, prin localizarea celor doua mari ramuri economice (agricultura si industria) se schiteaza principiile generale de organizare a teritoriului (generandu-se doua elemente spatiale de baza, ariile si punctele).
In modelul lui Alfred Weber se analizeaza localizarea unei intreprinderi care are o functie de productie cu coeficienti ficsi, intr-un spatiu omogen. Minimizarea costurilor de transport ramane criteriu principal al localizarii intreprinderilor. Firma utilizeaza mai multe resurse materiale, iar productia este destinata mai multor puncte de consum[3]. Clasificand resursele in functie de pozitia lor in spatiu si de transformarile suferite in procesul prelucrarii (daca pierd sau nu din greutate) Weber propune mai multe tehnici de localizare a firmei:
a) Metoda listei de principii:
Materiile prime sunt clasificate in raport de un indice de prelucrare:
Localizare activitatilor in raport cu indicele de prelucrare, localizarea surselor de materii prime si a pietei de desfacere este prezentata in tabelul nr. 1.
Tabelul nr. 1. Localizarea intreprinderii conform metodei listei de principii
|
Tip materii prime |
Localizare centru prelucrare |
|||||
|
Libere |
Pure |
Pierd greutate |
Loc mat. Prima |
Loc consum |
Loc intermed. |
Zone indstr. |
|
L | ||||||
|
P | ||||||
|
M1 | ||||||
|
L1+L2 | ||||||
|
P1+P2 | ||||||
|
M1+M2 |
| |||||
|
L |
P |
M1 | ||||
|
L |
P |
M4 | ||||
Se observa ca in cazul materiilor prime libere (L) si a celor pure (P) intreprinderea se va situa in proximitatea centrului de consum. In cazul materiilor prime care pierd din greutate M1 amplasarea intreprinderii va fi situata la locul de producere a materiilor prime pentru a transporta spre piata doar produsul finit "mai usor", deci cu cheltuieli de transport mai mici.
Combinatiile de doua materii prime libere, sau a doua materii prime pure vor determina localizarea intreprinderii tot in proximitatea pietei. In schimb combinarea a doua materii prime cu inidici de prelucrare diferiti va determina o localizare a intreprinderii intr-o zona intermediara, pentru ca trebuie sa se tina cont de situarea ambelor surse de materii prime.
Combinatiile a trei surse de materii prime presupun doua alternative:
Situarea intreprinderii intr-o zona industriala, ceea ce presupune exploatarea avantajelor existentei unei infrastructure, dar si un compromis intre localizarea sursei de materie prima care pierde din greutate si a centrului de consum;
Situarea intreprinderii la locul de producer a materiei prime care are un indice ridicat de prelucrare (4 - M4). Consideram ca in acest caz o tona de produs finit presupune consumul a 4 tone din M4, si a cate o tona din materia prima L si P. Amplasarea intreprinderii in centrul de consum ar insemna cheltuieli de transport pentru 5 tone de materii prime la o tona de produs. Dar, amplasarea intreprinderii la locul de producere a materiei prime M4, ar insemna cheltuieli de transport pentru o tona de materie prima P si o tona de produs.
b) Metoda compunerii vectorilor:
Tehnica se bazeaza pe compunerea vectoriala, numita si triunghiul lui Weber, imprumuta metoda din mecanica. Vectorii reprezenta potentialele fluxuri de transport spre sursele de materii prime si punctul de desfacere (vectorii vor fi orientati spre aceste puncte, iar modulul lor va fi proportional cu marimea estimata a cheltuielilor de transport). Compunerea vectorilor se relizeaza, fie prin metoda insumarii paralele, fie dupa regula paralelogramului (fig. nr. 2.3).
C unde:

 M1, M2 -surse de materii
prime;
M1, M2 -surse de materii
prime;
![]() C
- centrul de consum;
C
- centrul de consum;
![]() T0
- optiunea initiala de
T0
- optiunea initiala de
![]()
![]()
![]() T1 T0 amplasament
T1 T0 amplasament
T - solutia finala de amplasament
![]() M1
M1
M2
Fig. nr. 2.3. Amplasarea unei intreprinderi prin metoda compunerii vectoriale (a lui Weber).
Se traseaza pe o harta un triunghi avand ca varfuri punctele unde sunt localizate sursele de materii prime (M1, M2) si centrul de consum (C). Se considera un punct initial T0 din interiorul triunghiului in care ar putea fi amplasata intreprinderea. Din acel punct se traseaza vectori orienatati spre varfurile triunghiului (modulele vectorilor vor fi proportionale cu cheltuielile de transport). Din varful unuia dintre vectori se duc paralele successive la ceilalti vectori. In varful ultimei paralele se va afla noul punct de amplasare a intreprinderii T1. Punctul T1 devine originea altor vectori care prin compunere vor determina un alt punct de amplasament T2. Procedura se repeta pana cand distanta dintre doua puncte successive (Tk-1, Tk) devine mai mica decat o marja de distanta fixata anterior.
c) Metoda geometrica
Metoda consta in construirea curbelor de cost egal de transport - isodapanelor. Aceasta presupune identificarea acelor puncte din plan, unde costurile de transport au aceesi valoare si apoi unirea lor prin curbe. Firma va fi amplasata pe isodapana cu cel mai mic cost.
Isopadana: locul geometric obtinut prin unirea punctelor care genereaza un acelasi cost total.
Vom considera urmatorul exemplu. Pentru a produce o tona dintr-un anumit bun sunt necesare doua tone de materie prima M1 si o tona de materie prima M2. Costul de productie al bunului pana la poarta intreprinderii (cost terminal). Cheltuielile de transport sunt de o unitate monetara pe tona transportata (fie aceasta materie prima sau produs finit). este de o unitate monetara pe tona de produs finit. Prin urmare:
Costul unei tone de produs finit este de 2 u.m. (pentru M1) + 1 u.m. (pentru M2) + cheltuielile de transport pe fiecare km parcurs. Vor fi generate urmatoarele serii de cercuri pornind din punctele de localizare a centrelor de materii prime si a centrului de consum:
Ø Dinspre sursa de materie prima M1, produsul finit s-ar realiza cu urmatorul cost unitar = 1 u.m. (cost terminal) + 2 u.m. (pentru producerea necesarului de materie prima M2). Aceasta inseamna ca primul cerc va avea o raza de 3 unitati, urmatoarele crecand cu un pas unitar (pentru fiecare unitate de produs finit transportata);
Ø Dinspre sursa de materie prima M2, produsul finit s-ar realiza cu urmatorul cost unitar = 1 u.m. (cost terminal) + 1 u.m. (pentru producerea necesarului de materie prima M1). Aici primul cerc ve fi de raza doua unitati, urmatoarele cercuri avand raze ce cresc cu pas unitar;
Ø Dinspre centrul de consum costul unitar al produsului finit ar fi = 1 u.m. (cost terminal) + 2 u.m. (pentru M2) + 1 u.m. (pentru M1). Primul cerc va fi de raza 4, urmatoarele cercuri avand raze ce cresc cu pas unitar;
Punctul de localizare a intreprinderii va insuma toate aceste costuri sub forma unor isopadane. De exemplu, punctul X din figura 2.4. este situate pe isopadana de 22 u.m., aflandu-se la intersectia cercului de 10 u.m. dinspre M1, cu cercul de 4 u.m. dinspre M2 si cu cercul de 8 u.m. dinspre centrul de consum C (10 + 4 + 8 = 22). In final, intreprinderea va fi amplasata in interiorul isopadanei minime de 20 u.m. (in punctul A).

Figura 2.4. Localizarea unei intreprinderi conform metodei geometrice[4].
d) Metoda algebrica.
Reprezinta o determinare analitica a coordonatelor in plan ale intreprinderii. Vom considera un system de axe carteziene (Ox, Oy). In acest system putem reprezenta coordonatele unui reper (loc de producere al materiei prime, sau piata), R(xi,yi) - de coordonate cunoscute si punctul in care va fi localizata intreprinderea A(x,y) - coordonate necunoscute.

Criteriul de optimizare este dat de minimizarea cheltuielilor de transport T:
Min(T) = Min t(g1d1 + g2d2 + g3d3)
Unde:
t - tariful unitar (pe tona-km) de transport
gi - greutatile bunurilor transportate, i = 1, 2, 3
di - distantele de la fiecare centru (de productie a materiilor prime, sau de consum) la punctul de amplasament al intreprinderii.
Din aceasta perspectiva obiectivul de optimizare poate fi rescris astfel:
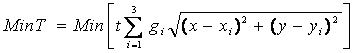
Determinarea punctului de minim presupune anularea derivatelor partiale ale functiei de transport in raport cu fiecare variabila care defineste coordonatele de localizare a intreprinderii:
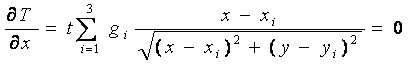
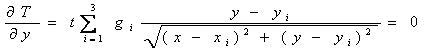
Rezolvarea acestui sistem cu doua necunoscute, duce la determinarea coordonatelor optime de amplasare a intreprinderii.
Conexiunea optimizare interna - optimizare externa
Odata stabilita localizarea intreprinderii, va trebui sa se optimizeze procesul de productie astfel incat sa maximizeze profitul. Aceasta presupune doua aspecte:
o abordare inerioara - conform teoriei economice neoclasice prin isocuante, curbe de costuri si niveluri de pret etc;
o abordare exterioara - in functie de schimbarile care survin in spatiul de actiune al intreprinderii.
Modelul lui Predhl
Cel care a abordat pentru prima data problema corelarii metodei neoclasice de optimizare a activitatii intreprinderii cu elementele de optim spatial a fost Andreas Predhl. In 1925 Predhl publica articolul Das Standorts-problem in der Weltwirtschaftstheorie, punand bazele "microeconomiei spatiale". Ideea de baza a acestui articol este ca teoriile spatiale si teoriile economice generale se puteau integra perfect, intrucat solutia unei probleme de economie spatiala tine, prin forta lucrurilor, de o interdependenta perfecta intre cele doua aspecte ale sale. In figura se ilustreaza aceasta idee pe cazul unei isocuante cu doi factori de productie f1 si f2.
Cuadratul f1- f2 reprezinta spatiul de productie neoclasic, iar cuadratul x-y reprezinta un spatiu metric. Orice schimbare in conditiile economice generale (de exemplu, o schimbare a returilor relative ale factorilor de productie la iesirea din fabrica) sau spatiale (o schimbare a costurilor relative de transport) va afecta atat utilizarea relativa a faxtorilor de productie, cat si localizarea unitatii de productie. In graficul, punctele A si B descriu doua situatii de acest tip.
In termeni mai formali sistemul predohlian cuprinde trei grupe de ecuatii:
ecuatii ce descriu conditiile neoclasice (egalitatea productivitatilor marginale relative si a preturilor relative ale factorilor de productie; respcetiv functia de productie corespunzatoare);
ecuatii de localizare de tip Weber;
ecutii de legatura a primelor doua prin intermediul costurilor de transport si a preturilor de livrare.
Rezolvarea sistemului de ecuatii are loc printr-un algoritm iterativ.
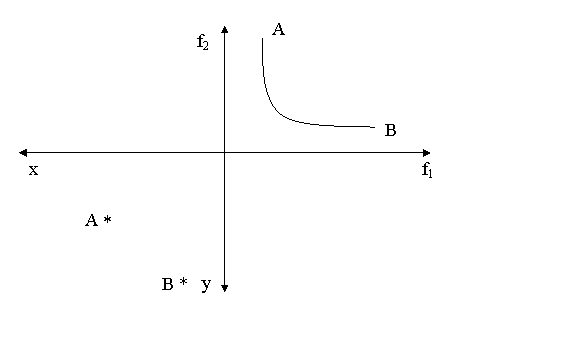
Figura nr. Corelarea izocuantei cu localizarea unitatii de productie conform Predhl.
Problema corelarii teoriei localizarii cu teoria economica neoclasica va fi reluata mai tarziu de catre August Lsh in incercarea de a identifica o solutie spatiala a echilibrului general al pietelor.
Odata amplasate intreprinderile vor incepe competitia pentru anumite piete locale. Daca vom considera mai multe centre de productie si mai multe centre de consum apare problema impartirii zonelor de piata intre intreprinderile localizate in acele centre de productie. Aplicata in mod consecvent la problematica teoriei economice traditionale, teoria localizarii sesizeaza in mod corect ca pietele au o dimensiune teritoriala reala, iar concurenta dintre firme nu se desfasoara pe o piata adimensionala abstracta, ci pe piete extinse teritorial. Se pun astfel bazele teoriei ariilor de piata.
Modelul lui Hotelling
Un secol dupa von Thnen , economia spatiala pune problema invers : piata este considerata dispersata in mod regulat pe tot teritoriul, iar intrebarea este cum isi vor repartiza intreprinderile aceasta piata.
Hotelling analizeaza un duopol spatial liniar[6], considerand o piata liniara si doi vanzatori. Exemplul clasic este plaja si doi vanzatori de inghetata. Se condera un amplasament initial al vanzatorilor de inghetata :
A B
![]()
![]()
![]()
![]()
![]()
![]()
Persoanele aflate pe plaja vor dori sa cumpere inghetata a.i. sa se deplaseze cat mai putin. Prin urmare cei ce vor fi amplasati in extremitatea stanga a segmentului de plaja vor apela la vanzatorul A, iar cei din extremitatea dreapta a segmentului vor apela la vanzatorul B. Consumatorii dintre cei doi vanzatori se vor apela la unul dintre cei doi vanzatori prin partajarea egala a segmentului AB. Cum cei doi vanzatori sunt in competitie, fiecare ca cauta sa acopere un segment cat mai mare din clientela. Prin urmare vor avansa spre zona dintre ei . Presupunem ca vanzatorul A se extinde mai mult :
A B
![]()
![]()
![]()
![]()
![]()
![]()
Incercand sa acapareze cat mai mult din piata lui B, vanzatorul A va deservi mai putin bine extremitatea din stanga a plajei, a.i. o parte din clienti vor renunta la serviciile sale (apeland la bunuri substituibile). Sesizand noua oportunitate Vanzatorul B va patrunde in zona de piata a lui A (care este mai mare) :
B A
![]()
![]()
![]()
![]()
![]()
![]()
Vanzatorul v-a cauta sa-si extinda noul segment de piata, a. i. Frontiera dintre cei doi se va situa la jumatatea plajei.
B A
![]()
![]()
![]()
![]()
![]()
![]()
In final cei doi competitori (considerati de forte egale) vor constata ca cea mai buna acoperire a jumatatilor de plaja se obtine prin amplasarea mediana in jumatatile initiale ale segmentelor de piata.
![]()
![]()
![]() A B
A B
![]()
![]()
![]()
Se obtine astfel un echilibru concurential stabil pe acea piata..
Concluzii :
a) In conditii de concurenta perfecta exista tendinta de localizare mediana a activitatilor ;
b) Din a) rezulta o crestere a gradului de concentrare ;
Hotelling presupune preturile cunoscute si localizarile necunoscute. Palander presupune localizarile ofertantilor cunoscute si se intreaba cum se fixeaza limitle ariilor lor de piata si preturile practicate. Intrebarea este : localizarile schimba preturile, cotele de piata sau profiturile ?
Costurile de productie sunt cunoscute, acestea devin costurile de distributie care devin strategice.
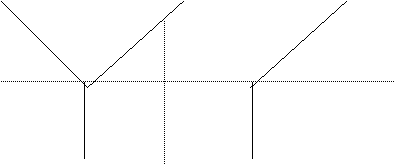
Fig. 2. arata limitele de influenta a doi ofertanti caand costurile de productie sunt identice (masurate prin segmentul vertical).
Iar costurile de distributie sunt masurate prin pantele dreptelor care pleaca din A si B.
Se face ipoteza ca cumparatorul plateste exact costul total de productie.
![]() CD
CD
CP1
![]()
A B X
Figura nr. Costurile de productie si custurile de distributie pentru doi producatori A si B
Unde X latimea frontului de piata ; patrunderea in interiorul pietei depinde de costurile de productie (CP) si de cele de distributie (CD).
Se pot observa situatiile :
costurile de productie si de transport sunt egale ;
costurile de productie diferite iar costurile de transport sunt egale ;
costurile de productie sunt egale iar costurile de transport sunt diferite.
Astfel Palander aprofundeaza fin teoria duopolului, intelegand ca spatiul suprima concurenta perfecta. Fiecare intreprindere dispune de o pozitie privelegiata in raport cu consumatorii din vecinatatea sa.
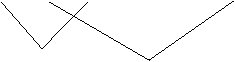
Presupunem ca o intreprindere deja instalata este situata acolo unde costurile de productie sunt cele mai mici si ca acestea cresc pe masura ce ne indepartam de punctul A. Intreprinderea noua se va instala in proximitate (B) chiar daca intra in concurenta cu intreprinderea deja existenta, sau va cauta o pozitie periferica (C) pentru a beneficia de protectia prin distanta? (D.M. Smith - 1971). Daca se simte suficient de puternica intreprinderea noua se va amplasa in proximitatea ariei de piata a intreprinderii vechi, cele doua firme intersectandu-si ariile de piata. Se poate observa ca intreprinderea noua se va concura cu intreprinderea deja amplasata pe piata doar in zona data de intersectiile ariilor lor de piata.
In cazul in care intreprinderea noua este de putere mai mica decat intreprinderea deja amplasata pe piata, va fi preferata o localizare mai departata, a.i. aria de piata a firmei noi sa nu se intersecteze cu aria de piata a firmei vechi. Astfel, firma noua se protejeaza prin distanta de concurenta firmei vechi.
![]() P
P
![]()
![]()
![]() P0
P0
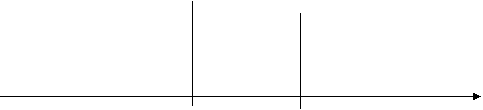
C B A distanta
Distributia ariilor de piata:
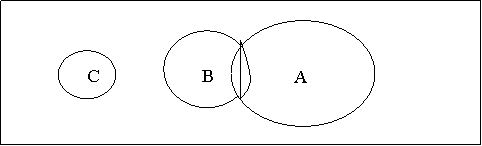
Figura nr. Aplasarea unei intreprinderi noi in raport cu o intreprindere deja existenta pe piata
Structurarea optima a teritoriului
Amplasarea centrelor de productie modifica geografia economica a unui teritoriu. Intreprinderile localizate creaza arii de piata in raport cu centrele de consum (localitati). In plus, intreprinderile localizate in anumite puncte din teritoriu, au nevoie si de forta de munca. Pentru a fi cat mai eficienta forta de munca trebuie sa se amplaseze cat mai aproape de intreprindere.
Aparea o intrebare noua in teoria localizarii cum se distribuie localitatile intr-un teritoriu? Altfel spus, cum structureaza localitatile un teritoriu?
In conformitate cu abordarile lui von Thnen si ale lui Weber, putem spune ca agricultura structureaza parcelele de teren, dar si zona rurala, pe cand industria structureaza zona urbana. Din acest punct de vedere structurarea unui teritoriu presupune o anumita matrice de configurare a retelelor urbane si a celor rurale. Intre cele doua tipuri de retele exista schimburi economice care pot afecta la randul lor modul de structurare a teritoriului.
Zona urbana
In lucrarea sa "Locurile centrale din Germania de Sud" , Walter Christaller isi propune sa determine principiile de baza care determina numarul, marimea si distributia asezarilor umane.
Ideea de baza a lucrarii este ca: "cristalizarea materii in jurul unui nucleu reprezina o forma elementara a ordinii in natura". Aplicarea principiului la distributia asezarilor umane are la baza rolul functional al localitatilor. Asfel, principala functie a unui oras este de a fi centrul unei regiuni, i.e. de a distribui bunuri si servicii pentru spatiu din care face parte. (functia de piata).
Intrucat orasele sunt de marimi si pozitii administrative diferite Christaller va folosi termenul generic de loc central, de unde si denumirea de teorie a locurilor centrale. Locurile centrale pot fi de nivel superior sau inferior. Christaller afirma ca: "importanta unui loc central nu este dovedita de dimensiunile fizice sau marimea populatiei ci de eforturile comune ale locuitorilor si de intensitatea cu care se straduiesc ei sa realizeze anumite sarcini esentiale". Din punct de vedere economic rangul unui oras este dat de importanta bunurilor furnizate in zona inconjuratoare. Cum in economie intervine principiul raritatii, valoarea fiind direct proportionala cu raritatea, vom avea o ierarhizare a bunurilor in functie de frecventa in consum. De exemplu, produse de bacanie se consuma zilnic, serviciile de distractii (entertaiment) se consuma in week-end, bunurile de arta se consuma si mai rar etc.
Este perfect logic, ca furnizorii de bunuri si servicii care se consuma zilnic sa fie situati mai aproape ce consumatori decat furnizorii de bunuri si servicii ce au o frecventa mai redusa in consum.
Considerandu-se un spatiu omogen, principiului pietei va impune ca orice punct din teritoriu trebuie sa aiba acces la toate bunurile si serviciile. Accesul in conditii egale presupune existenta unor localitatile echidistante in teritoriu. Daca vom considera arii circulare de piata conform lui Pallander se observa ca pot exista localitati in teritoriu care sa nu fie incluse in nici o arie de piata (figura )

Figura nr. Acoperirea defectoasa a teritoriului cu arii de piata circulare.
Pentru ca orice consumator
sa aiba acces la bunurile cu frecventa ridicata in consum, in conditii optim, este necesar ca orice
punct din teritoriu trebuie sa fie situat la o distanta fata de un loc central
de circa 4 km (o ora de mers pe jos). Intrucat localitatile sunt distribuite
echidestant in teritoriu, rezulta ca acel cumparator trebuie sa se situeze (sa
locuiasca) in ortocentrul unui triunghiului echilateral care are ca varfuri
locuri centrale de rang superior. Stiind ca intr-un triunghi echilateral
ortocentru este situat la 2/3 de orice varf (in cazul nostru 4km) rezulta ca
latura triunghiului echilateral este ![]() ≈ 7km. Uninad
sase triungiure echilaterale de acest tip se obtine o acoperire totala a teritoriului
sub forma unui hexagon (figura ). Mai mult intreg teritoriul va fi legat
printr-o structura de hexagoane de marimi diferite care au in varfuri locuri
centrale de diferite ranguri. Se observa ca in centrul hexagonului mare (de
latura 7km) se afla locul central de prim rang. In varfurile acestui hexagon se
afla locuri centrale de rang doi, iar in proximitatea locului central de prim
rang se afla un hexagon mai mic (de latura 4km) care are in varfuri locuri
centrale de rang 3 (cum este cazul localitatilor periurbane).
≈ 7km. Uninad
sase triungiure echilaterale de acest tip se obtine o acoperire totala a teritoriului
sub forma unui hexagon (figura ). Mai mult intreg teritoriul va fi legat
printr-o structura de hexagoane de marimi diferite care au in varfuri locuri
centrale de diferite ranguri. Se observa ca in centrul hexagonului mare (de
latura 7km) se afla locul central de prim rang. In varfurile acestui hexagon se
afla locuri centrale de rang doi, iar in proximitatea locului central de prim
rang se afla un hexagon mai mic (de latura 4km) care are in varfuri locuri
centrale de rang 3 (cum este cazul localitatilor periurbane).
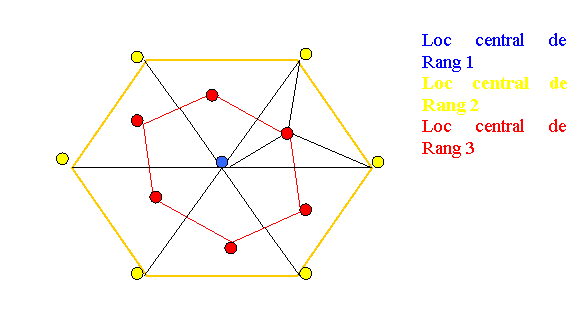
Figura nr. Acoperirea teritoriului cu structuri hexagonale de locuri centrale.
Coreland principiul pietei cu principiul minimizarii costurilor de transport (care cere cai de comunicatii drepte si scurte), va rezulta o retea de hexagoane concentrice care va acoperi intregul teritoriu cu locuri centrale de diferite ranguri. Astfel rute de transport drepte vor lega locurile centrale aflate in varfurile diferitelor tipuri de hexagoane.
Christaller adminte faptul ca rangul unui loc central depinde si de pozitia sa administrativa, dar demonstreaza faptul ca atunci cand spatiul este organizat dupa principiul administrativ vor fi necesare mai multe locuri centrale pentru a se obtine aceeasi eficienta spatiala ca in cazul organizarii dupa principiul pietei.
Prin urmare criteriile economice sunt mai eficiente in organizarea teritoriului, decat cele administrative.
Modelului lui Christarller a fost dezvoltat cu succes in analiza retelei urbane din S.U.A.. Un exemplu interesant al rezultatelor acestor studii il reprezinta legii lui Zipf , (legea rang dimensiune)..
Legea lui Zipf stabileste faptul ca populatia unui oras dat tinde, in medie, sa fie egala cu raportul dintre populatia centrului cel mai important si numarul de ordine al rangului orasului respectiv, rang determinat pornind de la dimensiune sa demografica:
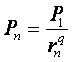
unde:
Pn - populatia orasului de ordin n;
P1 - populatia orasului celui mai important
r - rangul orasului
q - constanta pozitiva
Zona rurala si aparitia oraselor
Dupa cum s-a putut observa anterior, Christaller ofera o solutie la problema modalitatii de amplasare a oraselor in teritoriu, dar nu-si pune problema aparitiei oraselor. Aceasta din urma problema este abordata de August Lsch in lucrarea, Ordonarea spatiala a economiei .
Utilizand forta de munca pe scara larga, exploatatiile agricole necesitau in proximitatea lor numeroase localitati. Localitatile rurale se bazau in mare parte pe autoconsum (mai ales pentru bunuri alimentare), dar resimteau pregnant nevoia de produse mestesugaresti. Acest tip de cerere corelat cu principiul minimizarii distantelor determina gruparea localitatilor rurale in jurul unui centru mestesugaresc. Pe masura ce populatia localitatilor rurale sporea, crestea si cererea pentru bunuri manufacturizate, a.i. centru mestesugaresc crestea devenind oras. Pentru a-si satisface cererea de bunuri specifice activitatilor lor centrele mestesugaresti se organizau la randul lor in retele, in jurul unui centru mai mare, s.a.m.d. Lsch admite ca principiul pietei determina structurarea teritoriului cu retele hexagonale de localitati (conform lui Christaller).
Continuand cercetarile asupra mondului in care raporturile de piata determina organizarea teritoriului, Lsch intreprinde prima tentativa de corelare a teoriei localizarii de teoria echilibrului general al pietelor (Walras).
Ipoteze:
a) teritoriul este un plan omogen (populatia, materiile prime, activitatile agricole sunt egal distribuite). Prin urmare costurile de transport sunt liniare in raport cu distanta.
b) Cosumatorii preiau costurile de transport (sunt incluse in pret).
c) Randamente de scara sunt crescatoare.
Obiective cercetarii
Cum se localizeaza centrele de productie;
Cum se determina ariile de piata;
Cum se fixeaza volumul total al productei;
Cum se stabilesc preturile in teritoriu.
Restrictie: Toti consumatorii trebuie sa aiba acces la bunuri.
Altfel spus: Problema generala: Compatibilizarea maximizarii profitului intreprinderii cu acoperirea integrala a teritoriului (optimizarea intregului sistem).
Losch redefineste aria de piata a unei intreprinderi tinand cont de curba cererii pentru un anumit bun (figura ).
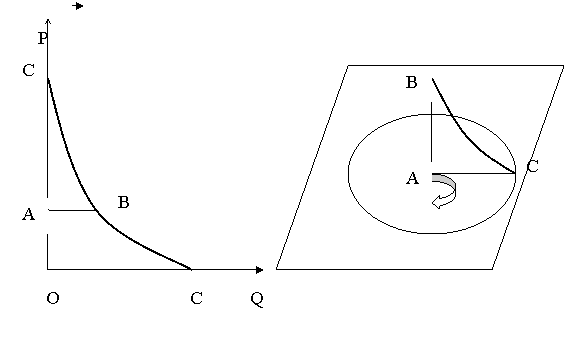
a) b)
Figura nr. Generarea ariilor de piata pornind de la curba cererii unui bun.
OA - limita pretului la care sunt acoperite integral costurile productiei (cost de transport nul). Peste aceasta limita intervin cheltuielile de transport ceea ce duce la o crestere a pretului. Dar, cresterea pretului va determina scaderea cantitatii cerute, care va deveni 0 in punctul C (de pe axa pretului). Aceasta inseamna ca segmentul AC - masoara costul de transport.
Pentru a descrie aria de piata a firmei curba cererii va pivota in jurul segmentului AB (cost transport = 0). Asfel, teritoriul va fi acoperit cu conuri care au la baza cercuri de raze - cheltuieli de transport.
Considerand ca exista mai multi producatori pentru acel bun va rezulta un sistem de conuri ce va descrie sistemul ariilor de piata ale unei ramuri economice.
Daca exista concurenta perfecta (libera intrare/iesire) rezulta ca piata va fi partajata prin conuri de raze egale. In plus, orice intrare a unei noi intreprinderi va reduce aria de piata a intreprinderilor existente (reduce costurile de transport), dar va creste costul total mediu. Aceasta inseamna ca in conditii de concurenta productia, costurile de productie si transport identice. Din perspectiva spatiala, concurenta perfecta determina conuri de piata identice pentru toate intreprinderile. Totusi pentru a respecta principiul acoperirii integrale a teritoriului aceste conuri vor avea baze hexagonale.
Aplicand aceste reguli pentru mai multe bunuri rezulta un ansamblu de sisteme de conuri cu baze hexagonale (cate bunuri exista). Se formeaza un spatiu economic prin suprapunerea unor conuri diferite.
Desi tendinta spre concurenta perfecta ar presupune un numar foarte mare de intreprinderi si implicit o structura foarte complicata de arii de piata, exista totusi o limita a numarului de intreprinderi dat de compromisul dintre minimizarea costurile de transport si maximizarea economiilor de scara.
Pentru o corelarea optima a principiilor optimizarii neoclasice (bazate pe concurenta perfecta) cu optimizarea functionala a teritoriului ar trebui rezolvata o problema majora: determina piata o solutie a acoperirii teritoriului a.i. aceasta solutie sa fie stabila si optimala (in sens Pareto)?
Determinarea unei solutii viabile penru aceasta problema trebuie sa tina cont de anumite obstacole:
Intrarea noilor intreprinderi inseamna reducerea ariilor de piata, rezultand reducere economii de scara.
Intreprinderile deja amplasate vor fi tentate sa introduca bariere de intrare si/sau sa elimine alte intreprinderi deja amplasate.
Desi concurenta perfecta ar conduce la o dispersie completa a structurilor de intreprinderi in teritoriu, economiile de aglomerare determina o regrupare a acestora in jurul unui punct fix. Economiile de aglomerare sunt legate de numarul mare de consumatori din marile centre urbane.
Intrucat concurenta incalca principiul distribuirii echidistante a intreprinderilor in teritoriu, iar intreprinderile cauta sa-si protejeze ariile de piata, se tinde spre accentuarea concurentei imperfecte, motiv pentru care Lsch nu reuseste sa rezolve problema corelarii teoriei neoclasice cu teoria localizarii.
Problema integrarii spatiului intr-un model al echilibrului general al pietelor a fost reluata ulterior:
Ø Walter Isard, "Economia localizarii si a spatiului" - 1956
Ø Keneth Arrow & Gerard Debreu - 1957
Ø Thajlling Koopmans & Michael Beckman - 1957
Ø Michael Beckman - 1968
Studiile acestor reprezentanti de marca ai teoriei economice au relevat o serie de dificultati majore ale problemei integrarii totale a spatiului in economie:
Substituirea spatiala a factorilor de productie;
Externalitatile;
Preturile terenurilor;
Tipul de concurenta.
Interactiuni in structurile de localitati:
Considerand structurarea teritoriului incheiata din perspective localizarii tipurilor de activitati, a asezarilor umane si a ariilor de piata, apare acum problema interactiunilor care apar intre aceste elemente ale structurilor teritoriale. Vom analiza mai intai problema interactiunii dintre localitati (orase)
Efectele gravitationale.
Studiind rolul marilor orase in cadrul retelelor de localitati, economistii au observat ca acestea "exercita o atractie deosebita" asupra populatiei din teritoriile invecinate. Astfel, orasele mari reprezinta centre de piata foarte interesante (locuri de cumparaturi deosebite), centre de cultura, oportunitati de locuri de munca si de afaceri etc. Din acest motiv a devenit tentant utilizarea modelului legii atractiei universale (Newton), in studiul interactiunilor dintre localitati. Utilizand relatia de fortei de atractie gravitationala:

unde:
M1, 2 - masele corpurilor ceresti,
D - distanta dintre cele doua corpuri
A - constanta de proportionalitate
Se vor estima fluxurile de persoane (cuparatori) dintre doua orase:
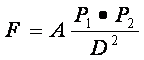
unde:
P1, 2 - populatia fiecarui centru urban,
D - distanta
A - constanta de proportionalitate
Sunt definite astfel doua principii ale interactiunilor dintre localitati:
Cel care aplica pentru prima data o astfel de relatie este William J. Reilly[10], formuland Legea lui Reilly (de atractie a comertului cu amanuntul): "in conditii normale, doua orase atrag comertul altui oras mai mic proportional cu populatia fiecarui oras si invers proportional patratul distantei de la acel oras la fiecare dintre orasele mari".
Forma analitica a aceste legi este urmatoarea:
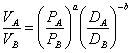 sau,
sau, 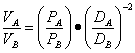
unde:
VA, B - vanzarile cu amanuntul in cele doua orase, catre locuitorii din orasul mic,
PA, B - populatia din fiecare oras mare,
DA, B - distantele de la orasul mic la orasele mari.
Pe baza relatiei anterioare se pot determina ariile de influenta ale celor doua orase mari. Se are in vedere faptul ca echilibrul zonelor de influenta ale celor doua orase mari se realizeaza acolo unde fortele de atractie sunt egale, respectiv unde fluxurile vanzarilor de bunuri sunt egale - VA = VB. Aceasta inseamna:
![]()
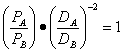 ↔
↔ 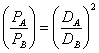
sau
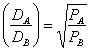
Fie DAB - distanta dintre cele doua orase mari
A B
![]()
DAB = DA + DB => DA = DAB - DB
Relatia distante - populatii devine:
![]()
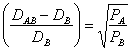 =>
=> 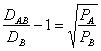 =>
=> 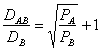
Populatia segmentului care uneste cele doua orase mari este atrasa de orasul B pana la limita distantei DB:
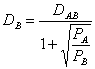
In mod similar avem:
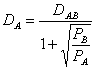
Se demonstreaza ca in afara segmentului AB zonele de influenta se repartizeaza astfel:
![]() , iar raza cercului
de influenta va fi:
, iar raza cercului
de influenta va fi:
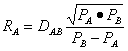
Pot sa apara modificari in distributia efectelor gravitationale cum ar fi neomogenitatea terenului (obstacole de transport), veniturile locuitorilor, tipurile de bunuri care sunt comercializate in fiecare oras, importanta administrativa a orasului etc.
Concluzii
Orasele mari atrag populatie din localitatile mici, pentru cumparaturi, dar si ca oportunitati de locuri de munca.
Distributia activitatilor pe langa orasele mari atrage si o distributie spatiala a fortei de muca. Tipurile de bunuri realizate in acele orase determina o diviziune teritoriala a fortei de munca.
Necesarul de forta de munca de calificare ridicata din orasele mari determina aparitia unor insitutii de invatamant superior, a unor institute de cercetari, a unor institutii culturale. Aceste elemente contribuie la randul lor la crestere fortei de atractie a oraselor mari. De aici rezulta economii de localizare pentru pentru intreprinderi (totalul distantelor spre utilitati este minim, iar oportunitatile de afaceri cresc). Din aces motiv fluxurile comerciale internationale sunt mai mari intre tarile dezvoltate decat intre cele in dezvoltare, respectiv cele dintre marile orase in raport cu orasele mai mici.
Limitele avantajelor de aglomerare sunt date de salariile mai ridicate pentru forta de munca din orasele mari (unde costul vietii este mai ridicat) si de externalitatile negative date de congestia spatiala. Din acest motiv Guvernul britanic a incercat sa introduca retrictii teritoriale pentru extinderea unor intreprinderi.
Prin efectele gravitationale exercitate, orasele mari tind sa creasca disparitatile reginale contribuind la depopularea unor localitati din zonele adiacente. Din acest motiv ponderea ridicata a zonelor urbane cat si distributia relativ echilibrata a acestora in teritoriu este foarte importanta pentru reducerea disparitatilor regionale.
Bibliografie:
Francis, R.L., Mirchandani, P.B., Discrete Location Theory, J. Wiley, New York, 1990
Fujita, M., Thisse, J-F, Economie des villes et de la localisation, De Beock & Larcier, Bruxelles, 2003
Garbovean, Ananie, Strategii si modele de dezvoltare regionala pentru zona Muntilor Apuseni, Editura Aeternitas, Alba Iulia, 2006
Greenhut, M.L., Norman, G., Hung, C.S,, The Economics of Imperfect Competition. A spatial Approach, Cambridge University Press, 1987
Jula, Dorin, Economie regionala, Editura Estfalia, Bucuresti, 2002
Jula, D., Ailenei, D., Jula, N., Garbovean A, Economia Dezvoltarii, Editura Viitorul Romanesc, Bucuresti, 1999
Conform Alfred Weber; ber den Standort der Industrien,; Tbingen, 1909. A se vedea ºi C.J. Friedrich; Alfred Webers Theory of the Location of Industries; Chicago University Press, 1929.
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 3319
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2025 . All rights reserved