| CATEGORII DOCUMENTE |
| Agricultura | Asigurari | Comert | Confectii | Contabilitate | Contracte | Economie |
| Transporturi | Turism | Zootehnie |
| Navigatie |
NoTiuni generale privind transportul forestier
Transportul forestier face parte din procesul de productie forestiera. El este constituit din transport de material lemnos, utilaje, personal silvic si materiale de intretinere si de cultura a padurilor.
Particularitatile transportului forestier
Prezinta importanta precizarea daca transportul are loc spre sau dinspre padure, cele doua feluri de transport fiind diferite. Spre padure se transporta: utilaje, oameni, materiale de intretinere si de cultura a padurii. Dinspre padure se transporta material lemnos si alte produse ale padurii.
Transportul forestier se desfasoara partial in padure si partial in afara ei.
Are un pronuntat caracter colector deoarece materialul ce se transporta este foarte raspandit.
Foloseste caile si mijloacele de transport, la intreaga lor capacitate doar intr-un sens (de la padure).
Are adesea un caracter periodic din cauza intervalelor lungi ce se scurg intre doua recoltari de material lemnos de pe o aceeasi suprafata de padure.
Materialul transportat este voluminos, perisabil si de greutate medie.
Traficul este scazut. El poate creste insa semnificativ in perioadele de exploatare. Viteza de circulatie este scazuta.
Alcatuirea transportului forestier
Transportul forestier se desfasoara pe uscat, pe apa si aerian. Pe uscat caile de transport sunt drumurile forestiere si caile ferate forestiere. Pe apa putem vorbi de transport cu plute sau alte ambarcatiuni, iar aerian, transportul forestier este constituit din funicularele forestiere.
Cel mai ieftin este transportul pe apa. Apare, insa, problema cursurilor de apa navigabile care sa se afle in vecinatatea fondurilor de exploatare. Transportul aerian este de asemenea ieftin dar necesita investitii ceva mai mari de constructie. Cel mai utilizat este insa transportul forestier rutier. Transportul feroviar forestiere se afla actualmente intr-un necontenit regres, desi transportul prpriu - zis pa calea ferata (fara a socoti investitia initiala) este mai ieftin ca cel rutier.
La toate acestea se adauga instalatiile provizorii de transport (drumuri de tractor, funiculare pasagere etc.).
Organizarea transportului forestier
O prima organizare a instalatilor de transport este in retele. Exista retele de colectare si retele de transport (propriu-zis).
3.1. Retelele de colectare
Aceste retele sunt constituite din instalatii provizorii (pasagere) de transport. Sunt ieftine si simple din punct de vedere tehnologic. Fac parte, din aceste retele, drumurile de tras, drumurile de alunecare, instalatiile hidrotehnice, instalatiile cu cablu etc.
Retelele de colectare asigura deplasarea lemnului (apropierea) de la locul de recoltare (de la cioata) pana la o platforma primara aflata langa o cale permanenta de transport.
Transportul in reteaua de colectare are loc in interiorul padurii si poarta denumirea de "colectare" sau "scos-adunat-apropiat".
3.2. Retelele de transport
Aceste retele asigura transportul forestier propriu-zis si cuprind caile permanente de transport. Ele servesc la deplasarea lemnului de la platforma primara, unde se pregateste materialul lemnos pentru incarcare, pana la centrele de prelucrare aflate langa un drum public sau langa un curs de apa navigabil.
Din punct de vedere economic, colectarea este mai scumpa decat transportul propriu-zis. Este deci necesar ca reteaua de colectare sa fie cat mai scurta, in favoarea retelei de transport propriu-zise.

Schema 1.1 retele de colectare/transport
Care sunt caracteristicile transporturilor forestiere?
Ce este reteaua de colectare?
Ce este reteaua de transport?
Capitolul II Drumuri
Scurt istoric al drumurilor
Vom prezenta istoricul tuturor drumurilor, nu numai al drumurilor forestiere.
Drumul trebuie pus in legatura cu inventarea rotii care a avut loc in jurul anului 5000 i.H. Cele mai vechi drumuri amintite in izvoarele istorice par sa fi fost cele din Mesopotamia construite cu prilejul ridicarii piramidei lui Kheops (3000 i. H.). Mai sunt amintite, apoi, drumurile ce legau Babylonul de Asia Mica (2000 i.H.).
Primele prescriptii tehnice de drumuri par sa dateze din jurul anilor 1000 i.H. si au aparut in China. Putin dupa aceea apar si primele procupari pentru intretinerea drumurilor in China, India si Persia.
Cei mai mari ingineri de drumuri ai antichitatii au fost romanii care din secolul IV i.H. si pana la inceputul erei crestine construisera deja o retea de 200000km. O serie de elemente tehnice de proiectare si executie le datoram romanilor (preferarea terasamentelor in umplutura, suprastructura stratificata - "sistem roman").
Urmeaza o lunga perioada in care nu s-au conemnat contributii la dezvoltarea tehnicii rutiere, pana in secolul XVIII si XIX cand apar sistemele de construire a pietruirilor si macadamului. Aceasta a fost ultima etapa inaintea aparitiei automobilului care a impus exigente noi.
In limba romana cuvantul drum provine din limba greaca - dromos.
In tara noastra distingem perioada drumurilor romane, ale caror urme se mai vad si astazi pe alocuri, dar mai cu seama o parte din drumurile actuale din Transilvania, Banat si Oltenia sunt pe infrastructura sau, macar, pe traseul partial al unor drumuri romane.
Urmeaza si la noi o lunga perioada de regres, in care au predominat drumurile naturale si cele de pamant, pana in epoca Regulamentelor Organice cand se face prima sistematizare a retelei de drumuri in Moldova si Tara Romaneasca. In celelate provincii romanesti existau deja astfel de sistematizari facute de catre administratia austriaca.
Urmeaza perioada drumurilor pietruite, din 1868, cand apare si prima lege a drumurilor, care constituie incepututul retelei rutiere actuale.
Din 1932 incepe perioada drumurilor moderne.
Alcatuirea drumurilor forestiere
In ceea ce priveste alcatuirea, drumurile forestiere nu difera esential de drumurile publice. Ele sunt alcatuite dintr-o suma de elemente geometrice si structurale destinate rezolvarii a doua categorii de probleme pentru vehiculele forestiere:
Invingerea dificultatilor de relief;
Dobandirea sigurantei si confortului in circulatie;
Elementele constructive ale drumurilor pot fi grupate in infrastructura si suprastructura.
Din infrastructura fac parte:
terasamentele (compuse din sapaturi si umpluturi de pamant);
sprijinirile (ziduri de sprijin, contraforti etc.);
lucrarile de asanare a amplasamentului sau a diverselor elemente constructive ale drumului (in principal, drenuri);
lucrari de protectie (pereuri, inierbari, cleionaje etc.);
lucrari de aparare - consolidare (santuri, rigole etc.);
lucrari de arta (poduri, podete, tuneluri).
Suprastructura este alcatuita din suprafata carosabila (calea) care se consolideaza printr-un sistem rutier si acostamentele care protejeaza calea. Calea impreuna cu acostamentele formeaza platforma drumului.
Intersectia unei suprafete verticale, ce trece prin mijlocul profilelor transversale ale drumului, cu suprafata superioara a platformei formeaza axa drumului. Aceeasi suprafata, la intersectia cu suprafata terenului, formeaza traseul drumului. Tot prin termenul de traseu se intelege, uneori, proiectia axului drumului pe un plan orizontal.
Proiectia orizontala a axei drumului se constituie in planul de situatie al traseului. Acesta este o insiruire de aliniamente care formeaza poligonul de baza; unghiurile dintre aliniamente sunt racordate prin arce de curbe, traseul definitiv devenind, astfel, o insiruire de aliniamente si curbe.

Fig. 2.1 Planul de situatie al traseului
Proiectia verticala a axei drumului (numita si linie a proiectului, linie rosie sau directrita) intra in componenta profilului longitudinal al drumului. Linia rosie este alcatuita din panouri caracterizate de lungime (pas de proiectare) si declivitate. Panoul reprezinta distanta dintre doua puncte succesive de schimbare a declivitatii. Panourile orizontale se numesc paliere iar cele inclinate se numesc rampe - daca drumul urca, respectiv pante - daca drumul coboara. Sensul de parcurgere este sensul hectometrajului. Alaturi de aceasta proiectie, in profilul longitudinal al drumului, se mai figureaza si linia terenului numita si linie neagra). Punctele de intersectie, dintre linia neagra si cea rosie, se numesc puncte de pasaj.
Prin plan de situatie al drumului se intelege proiectia orizontala a tuturor constructiilor si amenajarilor drumului.
Partile laterale inclinate din profilelor transversale alcatuiesc taluzele.

Fig. 2.2 Alcatuirea drumurilor forestiere. Profile transversale
In figura de mai sus, punctul C reprezinta muchia taluzului, iar punctul D se numeste creasta taluzului. Punctul B este piciorul taluzului.

Fig. 2.3 Profilul longitudinal al drumului

Fig. 2.4 Planul de situatie al drumului

Fig. 2.5 Profil transversal al drumului. Sectiune transversala
Elemente de dinamica a interactiunii vehicul - drum
Cunoasterea interactiunii vehicul - drum este importanta pentru proiectarea, mai cu seama, a suprastructurii drumului, adica pentru gasirea celor mai adecvate amenajari necesare sigurantei si confortului in circulatie.
3.1. Forte generate la contactul dintre vehicul si drum
Aceste forte apar pe suprafata urmei rotii. Ea este elipsoidala dar poate fi considerata, in mod aproximativ, circulara.

Fig. 2.6 Urma rotii simple si duble
Astfel, fortele ce apar pe urma rotii sunt:
Forte verticale provenite din sarcini statice sau dinamice. Ele solicita drumul si in adancime;
Forte orizontale (tangentiale) care pot fi longitudinale (cele de tractiune si cele de franare) si transversale (cele ce apar in curbe). Fortele orizontale solicita doar straturile superioare ale sistemului rutier.
Forta de tractiune - Ftr
Forta de tractiune face posibila deplasarea vehiculului doar daca depaseste toate rezistentele ce se opun deplasarii. Ea depinde de puterea motorului - N[kW] si de viteza de circulatie v[km/ora].
Astfel, relatia de calcul a fortei de tractiune este:
![]() , in care: (2.1)
, in care: (2.1)
![]() reprezinta un coeficient de randament ce ia valori
intre 0,85 si 0,95;
reprezinta un coeficient de randament ce ia valori
intre 0,85 si 0,95;
3.2. Rezistente intampinate de vehiculul in miscare
3.2.1. Rezistenta la rulare (tractiune) - Rt
Aceasta rezistenta provine din denivelarile drumului, din deformatiile elastice ale caii, dar si din deformatia elastica a pneurilor.

Fig. 2.7 Parametrii mecanici ai aparitiei rezistentei din rulare
Din figura de mai sus se observa ca:
tga=Rt/P a/r Þ Rt=P a/r;
Fie a/r=t, unde:
t reprezinta coeficientul de rezistenta la tractiune;
Atunci:
Rt=P t (2.2)
3.2.2. Rezistenta din declivitate - Ri

Fig. 2.8 Parametrii mecanici ai aparitiei rezistentei din declivitate
Din figura de mai sus se observa ca:
Ri= P sina
Acestei rezistente i se adauga, neconditionat, rezistenta din rulare: Rt=Pcosa t
In rampa rezistenta va fi: Rt+Ri = P(tcosa+sina
In panta rezistenta totala va fi: Rt - Ri = P(tcosa - sina
Dar deoarece unghiul a este suficient de mic, putem scrie ca :
sina tga = i, iar cos![]() =1,
in care:
=1,
in care:
i reprezinta declivitatea exprimata prin tangenta trigonometrica a unghiului de inclinare.
Atunci:
Rt + Ri = P(t i)
Mai sunt si alte rezitente dar de importanta mai mica pentru drumurile forestiere, dat fiind vitezele de circulatie destul de reduse.
3.3. Aderenta roata - drum - Fad
Aderenta roata - drum este esentiala pentru deplasarea vehiculului rutier pe drum. Fie Pr incarcarea ce o transmite o roata drumului. Fie j coeficientul de aderenta dintre roata si drum.
Fie Pad = SPr
Atunci:
Fad = Pad j (2.4)
Fad reprezinta forta de aderenta dintre vehicul si drum
Fata de cele de mai sus se pot scrie conditiile de miscare ale vehiculului:
Conditia ca roata sa ruleze:
Ftr ³ R, in care: (2.5)
R reprezinta rezistenta totala la deplasare (Rt + Ri);
Conditia de a nu aparea patinare (invartirea in loc a rotii neurmata de vreo deplasare):
Ftr £ Fad (2.6)
Asadar, conditia generala de circulatie a vehiculului devine:
Fad ³ Ftr ³ R
3.4. Franarea. Distanta de franare. Vizibilitatea
Franarea este un proces in care intervine frecarea intre saboti (sau, dupa caz placute sau/si tamburi) si roata pe de o parte - Ff, respectiv frecarea dintre roata si drum - Ffr.
Pentru a nu se produce blocarea rotii insotita de lunecarea acesteia, este necesar:
Ffr ³ Ff , in care: (2.8)
Ffr = Pf j unde
Pf este greutatea rotii franate;
j este coeficientul de frecare prin franare;
3.4.1. Distanta de franare - df
Distanta de franare se determina prin egalarea lucrului mecanic de franare cu variatia energiei cinetice a vehiculului, provocata de franare.
Ffr df = ![]() , Ffr = m g j
, Ffr = m g j
Þ df = ![]() (2.9)
(2.9)
Daca determinam distanta de franare din conditia de oprire a vehiculului, si nu de incetinire a acestuia, ca mai sus, atunci v2 = 0 si deci:
![]() (2.10)
(2.10)
Coeficientul 254 apare datorita faptului ca distanta de franare a fost exprimata in metri, viteza in kilometri pe ora, iar pentru acceleratia gravitationala - g s-a luat valoarea de 9,805 m/s2.
3.4.2. Vizibilitatea. Distanta de vizibilitate - D0
Asigurarea vizibilitatii este o problema de siguranta circulatiei.
Prin distanta de vizibilitate se intelege distanta pe care trebuie asigurate conditiile de vizibilitate. Ea se determina din conditia de oprire a vehiculului (distanta de vizibilitate trebuie sa fie mai mare decat distanta de oprire a vehiculului).

Fig. 2.9 Distanta de vizibilitate
In figura de mai sus notatiile au urmatoarea semnificatie:
s1 - spatiu de perceptie - reactie ( spatiul parcurs de vehicul in 0,75.1,5 secunde);
s0 - spatiu de siguranta (5.10m);
Deci:
D0 = 0,278 v + 0,0125 v2 + 5 [m] (2.11)
3.4.3. Vizibilitatea in curbe
Acest concept opereaza cu trei notiuni proprii: raza de vizibilitate (raza vizuala), curba de vizibilitate si camp de vizibilitate.
Raza vizuala este in lungul corzii intinse intre vehicul si obstacol (vezi figura de mai jos).
Raza vizuala se poate lua egala cu distanta de vizibilitate. In figura de mai jos, se observa ca vehiculul se considera ca ar rula la distanta de 1,5m de conturul interior al partii carosabile. In concavitatea curbei este necesara eliminarea tuturor obstacole susceptibile de a obstructiona vizibilitatea. O atentie deosebita trebuie acordata in debleuri cand va trebui ca sapatura sa fie sporita numai pentru a asigura vizibilitatea.
Infasuratoarea razelor vizuale descriu curba de vizibilitate.
Campul de vizibilitate este marginit de curba de vizibilitate.

Fig. 2.10 Curba de vizibilitate si campul de vizibilitate
3.4.4. Vizibilitatea in profil in lung
Dificultatea privind vizibilitatea in profil in lung, apare la racordarile convexe ale acestuia (vezi figura de mai jos). Raza vizuala se obtine unind ochiul conducatorului auto, considerat a fi la 1,20m deasupra suprafetei carosabilului cu un obstacol, considerat a se afla la inaltimea de 0,20m. Se dau mai multe pozitii ale vehiculului si obstacolului, distanta dintre ele ramanand constanta (egala cu distanta de franare - D0). Infasuratoarea acestor raze vizuale va da, si aici, tot curba de vizibilitate.

Fig. 2. 11 Vizibilitatea in profil in lung
3.5. Adaptarea elementelor geometrice ale curbelor din conditii de dinamica vehicul - drum
3.5.1. Inscrierea vehiculelor in curba
Deoarece in curba vehiculul ocupa o latime mai mare din suprafata platformei, este necesara supralargirea acesteia. Supralargirea se da pe partea interioara a curbei si are aceeasi panta transversala cu calea. Valoarea supralargirii este in functie de viteza de proiectare si de raza curbei, cu conditia ca raza sa fie mai mica de 300m. Vehiculul avut in vedere este ATF 20, care are gabaritul cel mai mare dintre toate vehiculele aflate in dotarea parcului auto forestier. Supralargirea se mentine constanta pe intreaga lungime a curbei circulare si se racordeaza pe aliniamentele care incadreaza curba, pe cate 10m.

Fig. 2.12 Supralargirea caii in curba
3.5.2. Amenajari cauzate de aparitia fortei centrifuge
Forta centrifuga - C
Forta centrifuga poate provoca derapaj sau chiar rasturnarea vehiculului.
Se determina cu relatia:
![]() , in care: (2.12)
, in care: (2.12)
C [daN]; v [km/ora]; P [daN] - greutatea vehiculului; R [m] - raza curbei.
Derapajul in curbe
Conditia pentru a nu avea derapaj:
C£P f Û ![]() , unde: (2.13)
, unde: (2.13)
f este coeficientul de frecare intre pneu si carosabil;
Acesta are valori in functie de starea si tipul imbracamintii carosabilului. Pe imbracaminte acoperita cu noroi sau cu polei, valoarea coeficientului de frecare poate scadea foarte mult, pana catre 0,03. Un bun coeficient de frecare este de 0,10.0,15. Daca depaseste aceste valori, curba incepe sa fie resimtita de calatori, diminuandu-se deci, confortul si ajungandu-se, in cazul unor imbracaminti foarte rugoase, sa dea senzatia ca vehiculul e pe cale sa se rastoarne. Din acest motiv, depasirea unor astfel de valori ale coeficientului de frecare impune inclinarea transversala a carosabilului catre interiorul curbei.
Coeficientul 127 apare din unitatile de masura neomogene ce apar in relatie si din valoarea acceleratiei gravitationale inclusa in relatie.
Suprainaltarea
Consta in ridicarea partii exterioare a curbei si se face pentru combaterea derapajului, respectiv sporirea confortului.

Fig. 2.13 Compunerea fortelor pe un profil transversal suprainaltat al unei curbe
In acest caz conditia de a nu avea derapaj devine:
f (P cosa + C sina) +P sina ³ C cosa (2.14)
Impartim relatia de mai sus prin cosa, notam tga = it (inclinarea transversala a drumului, consideram it f 0 si obtinem:
C £ P (f + it) (2.15)
De aici rezulta si raza minima din conditia de a nu avea derapaj:
![]()
![]() (2.16)
(2.16)
Semnul este pentru deverul negativ. Prin definitie, deverul pozitiv este panta transversala a drumului care se opune derapajului.
Rasturnarea vehiculului in curbe
Forta centrufuga, asa cum s-a mai spus, poate provoca si rasturnarea vehiculului in curba.

Fig. 2.14 Compunerea fortelor care pot conduce la rasturnarea
vehiculului in curba
In figura de mai sus e este ecartamentul; h este inaltimea la care este situat centrul de greutate.
Vehiculul se rastoarna atunci cand rezultanta R trece dincolo de punctul A. Conditia de stabilitate consta in satisfacerea inegalitatii: momentul fata de punctul A al fortelor care contribuie la stabilitate sa fie mai mare decat cel al fortelor care pot provoca rasturnarea.
![]() (2.17)
(2.17)
La curbele cu raza de peste 170m nu este nevoie de suprainaltare, indiferent de viteza de circulatie (care nu poate depasi 50km/ora la drumurile forestiere).
Ce forte apar la deplasarea vehiculului?
Ce rezistente se opun deplasarii vehiculului?
Care sunt efectele fortei centrifuge?
Ce este distanta de vizibilitate?
Ce este supralargirea?
Ce este suprainaltarea
Ce se intelege prin dever pozitiv?
Drumul in plan orizontal
Dupa cum s-a vazut, aliniamentele ce formeaza poligonul de baza se racordeaza prin arce de curba. Aceste racordari sunt, de regula, interioare unghiului dintre aliniamentele adiacente. Numai daca avem unghiuri mai mici de 40g este necesar sa se faca racordare exterioara, obtinandu-se, astfel, o sepentina.

Fig. 2.15 Racordarea unghiurilor poligonului de baza
Intre curbele de sens contrar este obligatorie introducerea unui aliniament (aliniament de redresare), pentru siguranta si confortul circulatiei. Acest aliniament este de minimum 1,4v, adica spatiul parcurs de vehicul in 5 secunde. In cazuri justificate se accepta si lungimi de 8,5m pentru aliniamentele de redresare, dar se reduce corespunzator viteza (restrictie de viteza).
Curbele de racordare pot fi circulare sau progresive.
Curbele sunt niste abateri geometrice proiectate. Ele sporesc rezistentele, iar amenajarile ce se proiecteaza nu le pot anula in toate cazurile.
4.1. Curbe circulare
4.1.1. Elementele principale ale curbelor circulare
Elementele principale ale curbelor circulare (vezi figura de mai jos) sunt:
b - unghiul dintre aliniamentele adiacente;
a - unghiul la centru al curbei;
T = VTi = VTe - tangenta;
B=VM - bisectoarea;
L=![]() - lungimea curbei;
- lungimea curbei;
TiF=x - abscisa mijlocului curbei;
FM=y - ordonata mijlocului curbei;
VTiO - sistemul de coordonate in care este reprezentata curba
TiV - abscisa;
TiO - ordonata;

Intre elementele curbei circulare exista urmatoarele relatii:
![]() (2.18)
(2.18)
![]() (2.19)
(2.19)
![]() (2.20)
(2.20)
![]() (2.21)
(2.21)
![]() (2.22)
(2.22)
4.1.2. Calculul si trasarea curbelor circulare
Lungimea minima a unei curbe circulare este egala cu spatiul parcurs in cinci secunde. Daca exprimam viteza in km/ora, iar lungimea minima a curbei in metri, atunci:
Lmin=1,4 v
Aliniamentul de redresare este tot 1,4 v, exceptional 10m.
Raza minima a curbelor circulare se poate determina din conditie de derapaj sau din conditie de inscriere a vehiculului in curba.
Trasarea curbelor circulare
Trasarea include operatiunea de pichetare a punctelor caracteristice ale curbelor circulare: Ti, Te, M(mijlocul curbei)
Ti si Te se obtin prin masurarea directa a lungimii tangentei pe fiecare latura a poligonului de baza, pornind din varful acestuia.
M se determina prin masurare pe bisectoarea unghiului din varful poligonului, a carei directie se determina cu teodolitul instalat in varful poligonului. B=VM. Se mai poate determina si prin masurarea abscisei TiF pe latura poligonului de baza si a ordonatei FM.
Trasarea suplimentara
Trasarea suplimentara se efectueaza ori de cate ori curbele sunt lungi si punctele mentionate mai sus devin insuficiente. De asemenea se mai utilizeaza la retrasarea unei curbe.
In functie de relief, vizibilitate si gradul de precizie dorit, se utilizeaza metode exacte (metoda ordonatelor pe tangenta, metoda coordonatelor polare) si metode expeditive (metoda sfertului, metoda prin intersectii etc.).
Metoda ordonatelor pe tangenta
Intr-un sistem de axe de coordonate atasat varfului de poligon, se dau valori abscisei si se calculeaza ordonata fiecarui punct.
![]() (2.23)
(2.23)
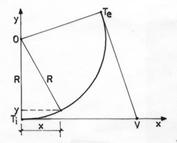
Fig. 2.17 Metoda ordonatelor pe tangenta
Materializarea punctelor obtinute poate fi facuta prin doua procedee: procedeul cu abscise egale si procedeul cu arce egale.
a) Procedeul cu abscise egale
Din Ti catre V se masoara distantele x, 2x, 3x,.si cu ajutorul echerului sau a prismei cu oglinzi se ridica ordonatele corespunzatoare.
Acest procedeu are dezavantajul ca nu da lungimile arcelor dintre punctele pichetate si care trebuie hectometrate.

Fig. 2.18 Procedeul cu abscise egale
b) Procedeul cu arce egale
Consta in impartirea arcului ![]() in parti egale:
in parti egale: ![]() ,
in care n reprezinta numarul de arce
egale. Se calculeaza unghiul la centru γ
corespunzator arcului elementar a.
,
in care n reprezinta numarul de arce
egale. Se calculeaza unghiul la centru γ
corespunzator arcului elementar a.
![]() , in care: (2.24)
, in care: (2.24)
R este raza arcului de cerc;
Coordonatele punctelor intermediare P1, P2,.(vezi figura de mai jos) se determina cu relatiile de mai jos:

Fig. 2.19 Procedeul cu arce egale
![]()
![]()
![]()
![]()
![]()
![]()
Exista si tabele de trasare care dau valorile x, y pentru diverse raze si valori ale arcului elementar.
Metoda coordonatelor polare
Pornind de la arcul elementar - a care poate proveni din arcul intregii curbe impartit intr-un numar egal de arce, se calculeaza unghiul la centru - γ.
![]()
Se calculeaza unghiul polar:
![]() (2.26)
(2.26)
Se aproximeaza raza polara - r cu arcul elementar - a.

Fig. 2. 20 Coordonatele polare
Aparatul goniometric se pozitioneaza in punctul - Ti cu zerourile in coincidenta si orientat catre varful poligonului. Se introduc pe rand unghiiurile δ, 2δ, 3δ s.a.m.d., aceste unghiuri dand directiile punctelor P1, P2, P3 s.a.m.d.
Cu ruleta deschisa la lungimea razei polare si fixata cu un capat in punctul Ti, se masoara pe directia de vizare si se determina punctul P1. Apoi cu un capat al ruletei in punctul P1 si pastrand deschiderea precedenta se intersecteaza directia urmatoare si se obtine punctul P2 s.a.m.d.

Fig. 2.21 Metoda coordonatelor polare
Care sunt elementele unei curbe circulare
Care sunt operatiunile, in teren, de trasare a unei curbe circulare
In ce consta metoda ordonatelor pe tangenta
In ce consta metoda coordonatelor polare
4.2. Curbe progresive
Date fiind conditiile de circulatie din curba in raport cu cele din aliniament, apare necesitatea unei curbe de trecere din aliniament in curba circulara care sa modereze efectele unei treceri bruste. Este vorba, in principal, de efectul fortei centrifuge. Aceasta este invers proportionala cu raza curbei. In aliniament raza este infinita, iar pe arcul de cerc aceasta capata o valoare finita.
Este necesara, asadar, o curba care sa faca descresterea progresiva a razei de curbura. O astfel de curba se numeste curba progresiva sau curba de tranzitie si din punct de vedere geometric, ea este o radioida (o conica).
Dat fiind cresterea fortei centrifuge in raport si cu viteza de circulatie, la drumurile forestiere curbele progresive se prevad pentru:
Viteze de 40km/h daca raza este sub 170m;
Viteze de 50km/h daca raza este sub 270m;
Viteze de 25km/h daca raza este sub 70m si exista perspectiva de a deveni drum public;
La cerere se pot introduce curbe progresive si incepand de la viteze de 30 km/ora .

progresive simetrice. Variatia curburii pe lungimea ansamblului
In figura de mai sus Ii si Ie sunt puncte comune curbei de tranzitie si aliniamentului, iar punctele Si si Se sunt puncte comune curbei de tranzitie si arcului de cerc.
4.2.1. Lungimea minima a arcului de curba progresiva
Aceasta lungime minima poate fi determinata dupa patru criterii:
empiric
mecanic (al limitarii acceleratiei normale; al limitarii acceleratiei unghiulare);
al rampei suprainaltarii
al confortului optic
Se introduce parametrul cresterea specifica in raport cu timpul a acceleratiei normale - j[m/s3], definit prin relatia de mai jos:
![]() , in care: (2.27)
, in care: (2.27)
an - acceleratia normala [m/s2];
t - timpul parcurgerii curbei progresive [s];
![]() , in care:
, in care:
L - lungimea minima a arcului de curba progresiva [m];
v - viteza de parcurgere a curbei progresive [km/h];
![]() , in care:
, in care:
R - raza arcului de cerc [m];
Atunci:
![]() (2.28)
(2.28)
Coeficientul 47 se datoreaza neomogenitatii unitatilor de masura.
La drumuri forestiere se accepta j=0,7m/s3.
Din considerente de confort acceleratia unghiulara se limiteaza la 0,02.0,05rad/s2.
Deoarece la intrarea pe arcul de cerc, dupa parcurgerea curbei progresive, viteza unghiulara devine:
![]() , in care
, in care
aw - acceleratia unghiulara, celelalte marimi au semnificatia cunoscuta;
Tinand seama de neomogenitatea unitatilor de masura, rezulta:
![]() (2.29)
(2.29)
Se bazeaza pe efectul optic care este un element psihologic, al desfasurarii traseului.
![]() (2.30)
(2.30)
Criteriul rampei suprainaltarii
Consta in impunerea conditiei ca rampa suprainaltarii sa se suprapuna ca lungime peste curba progresiva.
Asadar, pe aceasta lungime comuna trebuie sa se faca trecerea de la profilul transversal cu doua pante, specific aliniamentului, la profilul transversal cu o singura panta, eventual cu suprainaltare, specific portiunii de arc de cerc (virajului).

Fig. 2.23 Curba progresiva/rampa suprainaltarii
Conditia de mai sus poate fi transcrisa astfel:
![]() , in care: (2.31)
, in care: (2.31)
b - latimea carosabilului;
is - panta maxima a suprainaltarii (6.7%);
ir - declivitatea suplimentara, ir=i1-i, a marginii exterioare a carosabilului pe rampa
suprainaltarii;
i1 - declivitatea marginii exterioare a carosabilului;
i - declivitatea longitudinala in axul drumului;
Viteza maxima care rezulta prin aplicarea oricarui criteriu satisface conditia de stabilitate la derapaj.
La drumurile forestiere criteriul aplicat este cel mecanic al acceleratiei normale, pentru care exista si tabele care faciliteaza determinarea lungimii minime a curbei progresive.
Introducerea curbei de tranzitie poate fi facuta pe portiunea de traseu a arcului de cerc initial, sau numai partial pe aceasta portiune iar ce ramane, in zona aliniamentului. In acest ultim caz care - se va vedea mai tarziu - este mai avantajos, apare o deplasare a arcului de cerc ramas (a virajului) catre interior, prin reducerea razei virajului.

Fig. 2.24 Deplasarea virajului catre interior cu reducerea razei virajului
Din figura de mai sus, se observa ca:
![]() , in care: (2.32)
, in care: (2.32)
R+DR - raza cercului initial;
R - raza virajului;
IiSi = IeSe - curbele progresive;
O1 - centrul virajului, identic cu centrul vechiului arc de cerc;
Deplasarea virajului spre interior, operatiune numita si "stramutarea tangentei", poate fi facuta si pastrand raza arcului de cerc initial, dar deplasand centrul virajului in lungul bisectoarei.

Fig. 2.25 Deplasarea virajului catre interior prin pastrarea razei cercului initial
Din figura de mai sus se observa ca deplasarea in lungul bisectoarei are valoarea:
![]() (2.33)
(2.33)
4.2.3. Ecuatiile parametrice ale curbelor progresive
Obtinerea acestor ecuatii porneste de la conditia surprinderii modificarii razei traiectoriei vehiculului.

Fig. 2.26 Modificarea razei de curbura si a unghiului de bracaj la parcurgerea
unei curbe progresive de catre un vehicul auto
Relatia care descrie modificarea razei de curbura este cea de mai jos:
![]() , in care: (2.34)
, in care: (2.34)
La - ampatamentul vehiculului;
r raza de curbura progresiva egala cu raza de bracaj a rotii conducatoare (punctul F din centrul osiei din fata, vezi Fig. 2.26, descrie o curba progresiva);
q - unghiul de bracaj;
Presupunand ca vehiculul se deplaseaza cu viteza constanta - v, iar intoarcerea (viteza de bracaj) - w acceptam ca ar fi de asemenea constanta, si tinand cont ca:
![]() si
si
![]()
Atunci:
![]() , in care: (2.35)
, in care: (2.35)
t - timpul parcurgerii arcului de curba progresiva pana in punctul fixat;
s - lungimea arcului parcurs in timpul t;
Deoarece ampatamentul, viteza de circulatie si viteza unghiulara au fost presupuse constante, atunci:
![]() (2.36)
(2.36)
Aceasta ecuatie reprezinta o clotoida (numita si spirala radioidala; spirala lui Cornu; curba mecanica).
Daca aproximam arcul s cu coarda a, atunci:
![]() (2.37)
(2.37)
Aceasta ecuatie este ecuatia unei lemniscate ("Lemniscata lui Bernoulli").
Daca se aproximeaza arcul cu abscisa punctului (vezi figura de mai jos) se obtine:
![]() (2.38)
(2.38)
Aceasta ecuatie reprezinta o parabola cubica.
Parabola cubica se foloseste la calea ferata, iar la drumuri se foloseste clotoida.

Fig. 2.27 Clotoida
Arcul de clotoida dintre origine si punctul in care tangenta dusa la clotoida este perpendiculara pe abscisa se numeste "arc util de clotoida".
In general se foloseste doar portiunea dintre origine si punctul P (vezi figura de mai sus). La serpentine se foloseste intregul arc util.
4.2.4. Proprietatile clotoidei
Se noteaza:
![]() (2.39)
(2.39)
A reprezinta modulul (parametrul) clotoidei si are unitati de masura pentru lungimi.
In punctul final al clotoidei (care coincide cu primul punct de pe viraj) avem:
![]()
![]() de unde:
de unde:
![]() ,
iar, daca se considera lungimea minima a arcului de clotoida, atunci:
,
iar, daca se considera lungimea minima a arcului de clotoida, atunci:
 (2.40)
(2.40)
j fiind o constanta fixata de proiectant (j=0.5.0,7), rezulta ca modulul clotoidei depinde doar de viteza. Altfel formulat, inseamna ca fiecarei viteze ii corespunde un singur modul (si deci, o singura clotoida) care poate fi folosita pentru orice raza a virajului.
Pentru mai multe valori ale modulului se creeaza o familie de clotoide "omotetice", avand raportul de omotetie - Ω (raportul modulelor), iar ca centru de omotetie, originea sistemului de coordonate.

Fig. 2.28 Clotoide omotetice
Pentru doua clotoide omotetice este adevarat urmatorul sir de rapoarte egale:
![]() (2.41)
(2.41)
Semnificatia parametrilor din sirul de rapoaret egale poate fi observata in figura de mai sus.
Consecinta si avantajul este acela ca pentru un unghi φ - "variabila independenta" (are aceeasi valoare pentru toate clotoidele omotetice), denumit si unghi de intoarecere, un element oarecare al clotoidei se poate determina daca se cunoaste elementul omolog si modulul unei clotoide omotetice.
Clotoida de modul unitar A = 1 = Ω se numeste "clotoida de baza", caci cu ajutorul ei se pot alcatui tabele cu elementele clotoidelor.
4.2.5. Calculul elementelor clotoidei
Elementele ce se determina sunt: lungimea arcului de clotoida, coordonatele carteziene ale unui punct oarecare de pe clotoida si variabila independenta (unghiul de intoarcere.
Se stie ca:
![]() , unde:
, unde:
ds este arcul elementar;
dj este unghiul (variabila independenta) elementar;
S-a aratat ca:
![]()
Atunci:
![]()
Prin integrare se obtine expresia arcului:
![]() (2.42)
(2.42)
Tinand seama de cele scrise anterior, se pot calcula abscisa si ordonata oricarui punct de pe clotoida in functie de lungimea arcului de clotoida pana in punctul considerat si de modulul clotoidei. Prin integrare si dezvoltare in serie se obtine:
 (2.43)
(2.43)
Pentru unghiuri j< se poate aproxima x = s si ![]() .
.
Determinarea prin calcul a variabilei independente j
Tinand seama de (2.39) si de (2.42) rezulta:
![]() (2.44)
(2.44)
La intrarea in viraj valoarea variabilei independente devine:
![]() [rad] (2.45)
[rad] (2.45)
4.2.6. Definirea elementelor geometrice ale clotoidei
Aceste elemente sunt urmatoarele:

Fig. 2.29 Elementele geometrice ale clotoidei
j variabila independenta sau unghiul de intoarcere. Este unghiul dintre tangenta lunga la clotoida (dusa in origine) si tangenta scurta, dusa intr-un punct oarecare P (vezi figura de mai sus).
x si y coordonatele ortogonale ale punctului considerat P.
r si d coordonatele polare ale punctului P. Exista relatiile:
![]() si
si ![]() ; (2.46)
; (2.46)
Dr - deplasarea cercului catre interior.
x abscisa centrului de curbura a punctului considerat (P);
x distanta dintre abscisa punctului si abscisa centrului de curbura;
x - abscisa punctului;
Observam ca:
![]() (2.47)
(2.47)
b - normala (la tangenta scurta);
![]() (2.48)
(2.48)
n - abscisa piciorului normalei;
![]() (2.49)
(2.49)
g unghiul dintre raza polara si raza de curbura a punctului considerat;
t unghiul dintre raza polara si tangenta scurta;
4.2.7. Calculul si trasarea clotoidelor
In general se face cu ajutorul
tabelelor in care se intra cu unghiul de intoarcere - j sau cu variabila ajutatoare - t (![]() ).
Tabelele contin elementele principale ale clotoidei de baza, asa incat,
elementele clotoidei care se calculeaza, se determina prin multiplicarea
valorilor luate din tabel, cu valoarea parametrului - A al clotoidei careia
i se determina elementele.
).
Tabelele contin elementele principale ale clotoidei de baza, asa incat,
elementele clotoidei care se calculeaza, se determina prin multiplicarea
valorilor luate din tabel, cu valoarea parametrului - A al clotoidei careia
i se determina elementele.
Pentru trasarea unei clotoide ce se introduce intre un aliniament si un viraj (vezi figura de mai jos) trebuie determinate pozitiile punctelor Ii, Ie, Si, Se M. Viteza de proiectare fiind cunoscuta, raza virajului data de conditiile de teren sau determinata cu relatia (2.16), se impune cresterea j a acceleratiei normale, dupa care se determina lungimea minima a clotoidei cu relatia (2.28). Apoi unghiul de intoarcere cu relatia (2.45).

Fig.2.30 Trasarea racordarilor cu clotoide
Se folosesc relatiile:
![]()
![]() (2.50)
(2.50)
![]() (2.51)
(2.51)
![]() (2.52)
(2.52)
Este necesar ca a > j, iar lungimea virajului cel putin egala cu 0,277 v, deoarece virajul C' are expresia:
![]() (2.53)
(2.53)
a este unghiul la centru al arcului de cerc initial.
4.3. Serpentine
Serpentinle se introduc atunci cand unghiul din varful poligonului este mai mic de 40g, sau cand pentru invingerea declivitatii este necesara alungirea traseului.
Serpentina este un complex de curbe si aliniamente cuprinzand:
o curba principala, cu unghiul la centru de peste 200g, (vezi Fig. 2.31);
doua curbe auxiliare (secundare);
doua aliniamente intermediare;
Serpentina este de gradul (categoria) I-a daca cele doua curbe auxiliare au acelasi sens, sau de gradul(categoria) a II-a daca cele doua curbe auxiliare sunt de sensuri opuse, iar centrul curbei principale deplasat lateral fata de bisectoarea unghiului din varful poligonului.
Serpentina de gradul I este simetrica daca cele doua curbe auxiliare au aceeasi lungime si aceeasi raza si cele doua aliniamente intermediare egale.
Semiserpentina este o serpentina careia ii lipseste una din curbele auxiliare.

Fig. 2.31 Serpentina de gradul I simetrica avand centrul curbei principale in
varful poligonului
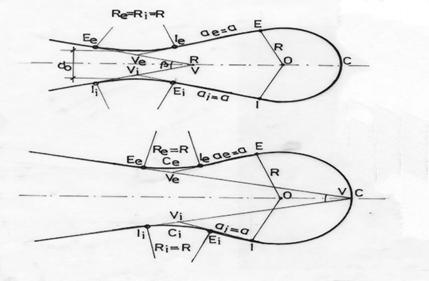

Fig. 2.32 Serpentine de gradul I simetrice avand centrele curbelor principale
deplasate in lungul bisectoarei unghiului din varful poligonului

Fig. 2.33 Serpentina de gradul I nesimetrica (Ri difera de Re)

Fig. 2.34 Semiserpentina

Fig. 2.35 Serpentina de gradul II
4.3.1. Calculul serpentinelor
Serpentina de gradul I
Serpentina de gradul I simetrica avand centrul curbei principale in varful poligonului

Fig. 2.36 Elementele geometrice de calcul ale serpentinei de gradul I simetrica
avand centrul curbei principale in varful de poligon
In figura de mai sus, prin consideratii geometrice elementare, rezulta:
Unghiul de
abatere al curbei auxuliare - ![]()
tg![]() =
=
![]() (2.54)
(2.54)
Tangentele curbelor auxiliare - T
![]() (2.55)
(2.55)
Unghiul la
centru al curbei principale - ![]()
![]() (2.56)
(2.56)
Distantele dintre V(O) si varfurile curbelor auxiliare - V1, V2
![]()
Lungimea curbei principale - L
![]() (2.58)
(2.58)
Lungimea totala a serpentinei - Lt
Lt=L+2L1+2a (2.59)
Distanta dintre mijloacele curbelor auxiliare - d0
![]() (2.60)
(2.60)
Serpentina de gradul I simetrica avand centrul curbei principale deplasat in lungul bisectoarei

Fig. 2.37 Elementele de calcul ale serpentinei de gradul I simetrice avand
centrul curbei principale deplasat in lungul bisectoarei
Distantele OO1=x1 se masoara. De asemenea ViVe = F. restul se dtermina prin calcul (vezi si figura de mai sus):
![]() (2.61)
(2.61)
 (2.62)
(2.62)
sin![]() (2.63)
(2.63)
![]() (2.64)
(2.64)
Serpentina de gradul II

Fig. 2.38 Elementele geometrice de calcul ale serpentinei de gradulII
In figura de mai sus, printr-o serie de consideratii geometrice elementare, rezulta:
 (2.65)
(2.65)
![]() (2.66)
(2.66)
![]() (2.67)
(2.67)
 -
- ![]() (2.68)
(2.68)
![]() (2.69)
(2.69)
![]() (2.70)
(2.70)
Unghiurile
![]() sunt "unghiurile de directie spre centrul
curbei principale".
sunt "unghiurile de directie spre centrul
curbei principale".
 (2.71)
(2.71)
 (2.72)
(2.72)
![]() (2.73)
(2.73)
Unghiurile
![]() se numesc "unghiuri de frangere ale
aliniamentelor initiale".
se numesc "unghiuri de frangere ale
aliniamentelor initiale".
![]() (2.74)
(2.74)
![]() (2.75)
(2.75)
![]() (2.76)
(2.76)
![]() (2.77)
(2.77)
![]() (2.78)
(2.78)
Tabel Elementele geometrice ale serpentinelor
|
Elementele serpentinei |
Viteza de proiectare [km/ora] |
|||
|
50 |
45 |
25 | ||
|
Raza minima a curbei principale [m] |
25 |
15 |
12,5 (10) |
|
|
Panta transversala maxima [%] |
6 |
6 |
6 |
|
|
Raza minima a curbei auxiliare [m] |
100 |
70 |
50 |
35 |
|
Declivitatea maxima in axul curbei principale [%] |
3,5 |
4(5) |
4(5) |
4(6) |
|
Lungimea minima a aliniamentului dintre curbele de sens contrar [m] |
50 | |||
|
Viteza de circulatie maxima pe curba principala [km/ora] |
25 |
25 |
15 |
10 |
4.3.2. Amplasarea serpentinelor
La amplasarea serpentinelor prevaleaza configuratia terenului, acest element fiind decisiv in alegerea tipului de serpentina si a unei mari parti din dimensiunile geometrice ale acesteia. Mai trebuie sa se tina seama de volumul de material lemnos ce se preconizeaza a se transporta, ceea ce hotaraste, cel mai adesea, raza curbelor serpentinei.
Se incepe, de obicei, printr-un studiu pe un plan cu curbe de nivel. Se incearca fixarea razei curbei principale care racordeaza exterior varful de unghi. Apoi, pe laturile unghiului ce se racordeaza, se studiaza amplasarea varfurilor unghiurilor curbelor auxiliare, avand grija sa fie suficient de departate intre ele pentru a nu se suprapune platformele. Urmeaza aliniamentele intermediare, si racordarile auxiliare.
Linia rosie pe serpentina va trebui sa asigure diferenta de nivel, dar si sa respecte declivitatea maxima admisa. Abia dupa aceasta, se va avea in vedere minimizarea volumelor de terasamente.
Ce sunt curbele progresive?
Ce este cotoida, lemniscata, parabola cubica
Care sunt proprietatile clotoidei?
Cum se determina elementele clotoidei?
Ce tipuri de serpentine cunoasteti?
Prin ce se deosebesc serpentinele de gradul I de cele de gradul II?
Cand devine necesara introducerea serpentinelor
Cum se face amplasarea serpentinelor?
5. Puncte de capat
Punctele initiale ale drumurilor forestiere se afla pe alte drumuri forestiere sau publice cu care se racordeaza, sau pe platformele unor centre de prelucrare sau preindustrializare care, la randul lor, se afla in vecinatatea unei cai de comunicatie.
Punctele finale se gasesc in interiorul padurii, pe platformele primare amenajate in vederea incarcarii materialului lemnos sau intr-o statie de intoarcere sau o bucla.
Drumurile forestiere pot avea ambele capete pe reteaua rutiera de transport forestier in cazul in care fac legatura intre doua bazine.
Racordarea drumurilor forestiere cu drumurile publice se face sub un unghi a carui valoare se stabileste astfel:
racordarea catre ambele sensuri ale unui drum public se face sub un unghi cat mai apropiat de 900 (vezi figura de mai jos);

Fig. 2.39
racordarea catre un singur sens se face sub un unghi cat mai mare (vezi figura de mai jos);

Fig. 2.40
In zona de platforma comuna se adopta declivitatea drumului existent si se asigura scurgerea apelor.
Jonctiunea drumurilor forestiere cu o cale ferata forestiera se face, de regula, in cea mai apropiata statie de cale ferata in care se asigura conditile de incarcare - descarcare, conditiile de platforma etc.
Jonctiunea cu un curs de apa navigabil sau flotabil se poate face cu conditia amenajarii unor locuri de depozitare, a unor instalatii pentru incarcarea slepurilor si/sau a plutelor.
Ce este punctul initial al unui drum forestier?
Ce este punctul final al unui drum forestier?
6. Statii si bucle de intoarcere
Statiile de intoarcere se amplaseaza, de regula, la capatul initial al drumului foretier, dar se pot amplasa si pe parcurs, daca sunt si vehicule care fac colectare pe parcurs si nu trebuie sa se deplaseze pana la capat.
Forma statiilor de intoarcere este dreptunghiulara cu dimensiuni 12.20 x 20.40m, iar declivitatea nu trebuie sa depaseasca 4%, exceptional 8%.
Buclele de intoarcere (vezi figura de mai jos) seamana cu serpentinele, dar nu au nevoie sa invinga vreo diferenta de nivel.

Fig. 2.41
La intoarcere vehiculele se deplaseaza cu viteza redusa(≈10km/ora) si se adopta elemente geometrice in consecinta.
Ce este o bucla de intoarcere?
Ce conditii trebuie sa indeplineasca o statie de intoarcere?
7. Intersectile drumurilor forestiere cu drumuri sau cu cai ferate
In principiu, trebuie evitate. Daca nu se pot evita, se va asigura un unghi al intersectiei cat mai aproape de 900 ,dar de min. 450, exceptional 300.
8. Statii de incrucisare
Se amplaseaza in locuri cu vizibilitate cat mai buna. Pentru drumuri cu o singura banda, aceste statii au dimensiunea 5,50.6,00 x 20,00m. Distanta intre ele trebuie sa fie de 300.400m. Din conditii de vizibilitate, statiile de incrucisare pot fi amenajate si in curbe. Banda suplimentara se amplaseaza pe partea dreapta a drumului in sensul transportului in gol si se cosolideaza cu un sistem rutier mai usor decat pe restul drumului.

Fig. 2. 42 Statie de incrucisare
Ce conditii trebuie sa indeplineasca o statie de incrucisare?
Ce rol au statiile de incrucisare?
9. Drumul in profil longitudinal
Studiul drumului in profil longitudinal consta, in principal, in studiul amplasarii liniei rosii. Acest studiu este interdependent de studiul traseului si de cel al profilelor transversale. In principiu, se urmareste asigurarea unei circulatii sigure si confortabile, ceea ce inseamna studiul declivitatii liniei rosii, dar si lucrari minime de terasamente si asigurarea unor conditii hidrologice cat mai favorabile.

Fig. 2.43 Elementele drumului in profil longitudinal
Cele de mai sus pot fi sistematizate in ceea ce se va numi cerinte pentru linia rosie. Acestea sunt:
respectarea declivitatilor maxime admise;
volume minime de terasamente cu posibilitate de compensare;
pozitionarea punctelor sau a cotelor obligatorii;
asigurarea unui pas de proiectare minim conform normativelor;
Pentru aliniamente si curbe cu raze mari, declivitatile admisibile variaza intre 7% (pentru 50km/h) si 9% (pentru 10km/h) la transport in plin, respectiv 8% si 12% pentru aceleasi viteze dar la transport in gol.
La curbele cu raze mici declivitatea maxima in axul caii conduce la o crestere a acesteia pe interiorul curbei (a carei lungime este mai mica)., de aceea, declivitatea li se reduce cu 1.3%.
Tabel Reducerea declivitatilor longitudinale maxime in curbele cu raze
mici
|
Raza curbei [m] |
50 |
45-40 |
35-30 |
25-20 |
15-10 |
|
Reducerea declivitatilor maxime [%] |
1,0 |
1,5 |
2,0 |
2,5 |
3,0 |
Se va avea grija la suprapunerea declivitatii in lung cu cea transversala la curbele amenajate in spatiu.

Fig. 2.44 Suprapunerea declivitatii in lung cu cea transversala la curbele amenajate in spatiu
Declivitatea minima este impusa doar de asigurarea scurgerii apelor (min. 0,5%)
Cotele din profilul in lung, se stabilesc dupa cum urmeaza: Cotele terenului se determina topografic in teren. Distanta intre doua puncte vecine in care se determina cota, nu va depasi 50m in terenurile accidentate si 100m in regiuni de ses. Cotele proiectului (fata superioara a imbracamintii in ax) se determina grafic fata de linia planului de comparatie in punctele de schimbare a declivitatii, iar in rest, pe baza de calcul in functie de declivitatea adoptata. Cotele de lucru sau de executie sunt diferentele intre cotele proiectului si cele ale terenului.
Pasul minim de proiectare (lungimea minima a panoului) variaza intre 100m (pentru 50km/h) si 20m (pentru 10km/h). Pasul minim de proiectare nu trebuie sa fie prea mic pentru a nu crea prea dese modificari ale regimului de miscare a vehiculului. Daca exista racordari verticale (ale liniei rosii), pasul minim de proiectare trebuie sa depaseasca suma tangentelor curbelor alaturate de racordare. Se vor evita schimbarile de declivitate pe portiunile curbe ale drumului.

Fig. 2.45 Pasul de proiectare minim
Portiunile cu declivitati mari se fragmenteaza pentru a nu se solicita prea mult franele.

Fig. 2.46 Fragmentarea declivitatilor
9.1. Racordarile verticale
Racordarile verticale sunt destinate racordarii unghiurilor dintre panourile vecine si sunt obligatorii doar daca diferenta dintre declivitatile vecine depaseste anumite limite. Acasta, pentru a se evita solicitarile mari in arcurile vehiculelor, create de forta centrifuga, alte neajunsuri legate de confort pentru racordarile concave, respectiv evitarea dificultatilor de vizibilitate la racordarile convexe. Se tine seama ca neajunsurile mentionate cresc odata cu viteza.
Exemplu: v=50, 40, 25 km/h - racordarile obligatorii sunt pentru diferente algebrice de peste 4% a declivitatilor; pentru v=20, 15, 10km/h obligativitatea racordarilor apare la diferente de peste 5%.
Racordarile fie convexe fie concave se fac cu arce de cerc, exceptional cu arce de radioida.
Unghiurile care se racordeaza pot fi masurate cu mare greutate, si de aceea, formulele de calcul contin unghiurile de inclinare ale panourilor.

Fig. 2.47 Racordarea declivitatilor convexe
![]()
Dar unghiurile ![]() fiind indeajuns de mici, se pot aproxima cu
valoarea tangentei trigonometrice care prin definitie este chiar declivitatea i
(
fiind indeajuns de mici, se pot aproxima cu
valoarea tangentei trigonometrice care prin definitie este chiar declivitatea i
(![]() ).
).
Deci:
![]()
Semnul + este pentru declivitati de sens contrar, iar semnul - pentru declivitati de acelasi sens.
De asemenea:
![]() (2.80)
(2.80)
Valoarea bisectoarei racordarii verticale modifica, in punctul de frangere, cota liniei rosii.
Tot astfel, in punctele de frangere:
![]() (2.81)
(2.81)
Lungimile racordarilor verticale nu se iau in considerare la calculul lungimii traseului drumului, contand doar evaluarile ce se fac in plan orizontal. De altfel, s-a vazut ca adesea, prin traseu se intelege proiectia axului drumului pe un plan orizontal.
Tabel Elementele geometrice in profil longitudinal ale drumurilor forestiere
|
Elementele geometrice |
U.M. |
Viteza de proiectare [km/ora] |
|||||
|
50 |
40 |
25 |
20 |
15 | |||
|
Rampa maxima la trransportul in plin |
7 |
7 |
8 |
9 |
9 |
9 |
|
|
Rampa maxima la transportul in gol |
8 |
9 |
10 |
11 |
12 |
12 |
|
|
Pasul minim de proiectare |
m |
100 |
80 |
50 |
40 |
30 |
30 |
|
Distanta de vizibilitate |
m |
90 |
70 |
40 |
30 |
20 |
20 |
|
Raza minima a curbei de racordare convexa |
m |
300 |
150 | ||||
|
Raza minima a curbei de racordare concava |
m |
700 |
400 |
200 |
150 |
80 | |
9.2. Puncte de cota obligata
Aceste puncte sunt stabilite de procesul tehnologic de exploatare a lemnului (punctele de concentrare ale materialului lemnos), respectiv alte impuneri date de configuratia terenului sau de exigente constructive ale cailor de comunicatii (incrucisarea cu alte drumuri sau cai ferate, posibilitatea traversarii cursurilor de ape, nivelul fata de acestea, cotele rampelor de acces la pod, gabarite, declivitatea impusa liniei rosii pe poduri, impuneri privind locurile de schimbare a declivitatilor liniei rosii pe poduri etc.).
9.3. Stabilirea pozitiei liniei proiectului
Pozitia liniei proiectului se studiaza, pe cat posibil, simultan cu traseul si profilele transversale, in raport de caracteristicile geotehnice, geologice, climatice si hidrologice si se refera la stabilirea:
In teren plan linia rosie se va aseza la o cota de 40.60cm. De principiu, drumul in umplutura se prefera celui in sapatura si aceasta pentru ferirea platformei de inzapezire si de umiditate excesiva. De asemenea pentru ca pamantul ce se introduce in ramblee poate fi selectionat.
In teren cu panta transversala intre 10% si 30% linia proiectului se va aseza la 15.20cm deasupra liniei terenului, daca se urmareste doar compensarea terasamentelor in acelasi profil (transversal). Aceasta datorita diferentelor de volum ale pamantului de aport fata de a celui sapat.

Fig. 2.48 Asezarea liniei proiectului in teren cu inclinare transversala drumului de
10%30%
La inclinari ale terenului de peste 30%, ceea ce este frecvent la traseele de coasta, se recomanda asezarea liniei rosii in asa fel incat sa conduca la obtinerea unui profil transversal in care cel putin doua treimi se afla in sapatura, pentru a se asigura o stabilitate mai mare a terasamentelor prin evitarea sprijinirilor, sau chiar in intregime in sapatura.
La drumuri situate in albia majora a cursurilor de apa (drumuri de vale) principala exigenta consta in asezarea platformei drumului la cel putin 0,50m deasupra nivelului apelor extraordinare.
In terenurile accidentate se urmareste cu precadere nivelarea cu ajutorul liniei rosii a neregularitatilor terenului, si deci o compensare longitudinala a terasamentelor. O astfel de compensare se obtine prin asezarea liniei rosii cu 15.20cm deasupra liniei care, aparent la un studiu pe plan, ar asigura compensarea debleu - rambleu. Explicatia este urmatoarea: profilele transversale sapatura/umplutura difera la inclinarea taluzurilor; cele de sapatura contin santuri si eventual banchete; prin sapare pamantul se afaneaza modificandu-si, deci, volumul si compactitatea.
La drumurile in debleu prevaleaza evacuarea apelor si pentru aceasta linia proiectului trebuie sa aiba o inclinare de cel putin 0,5%, precum si posibilitatea descarcarii santurilor.
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 6215
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2026 . All rights reserved