CATEVA PROBLEME DE MINIM IN SPATIU - clasa a VIII-a

SCOALA CU CLASELE I-VIII NR. 27, TIMISOARA

Introducere

Lucrarea de fata isi propune sa faca o sinteza a problemelor remarcabile de minim in spatiu.

In incercarea noastra de a fi cat mai bine intelesi de catre eventualii cititori am prezentat in prima parte a lucrarii delimitarea conceptuala a minimului, in contextul limbajului distantelor, urmate de constructii ale distantelor si de observatii utile solutionarii problemelor propuse.

Partea a doua a lucrarii prezinta cateva probleme mai generale de determinare unor distante optime, respectiv a unor arii minime determinate de puncte mobile din spatiu.

In continuarea lucrarii problemele generale se particularizeaza pe corpurile geometrice poliedrale studiate in decursul clasei a VIII-a, iar in final sunt prezentate cateva concluzii.

Ne exprimam speranta ca lucrarea noastra va fi utila cititorilor care doresc sa se pregateasca pentru examene sau alte concursuri scolare.

Cateva notiuni teoretice

Def. 1: Distanta dintre doua puncte in spatiu reprezinta lungimea segmentului determinat de punctele date.

d(A; B)AB x

Obs. 1 Distanta dintre punctele A si B reprezinta drumul minim de la punctul A la punctul B.

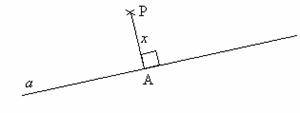
Def. 2: Distanta de la un punct la o dreapta reprezinta lungimea segmentului determinat de punct si piciorul perpendicularei construite din punct pe dreapta data.

Obs. 2 Distanta de la un punct la o dreapta reprezinta drumul minim de la punctul dat la un punct oarecare al dreptei date.

Def. 3: Distanta de la un punct la un plan reprezinta lungimea segmentului determinat de punct si piciorul perpendicularei construite din punct pe planul dat.

Obs. 3 Distanta de la un punct la un plan reprezinta drumul minim de la punctul dat la un punct oarecare al planului dat.

Def. 4: Distanta dintre doua drepte necoplanare in spatiu reprezinta lungimea segmentului determinat de picioarele perpendicularei comune pe dreptele date.

Obs. 4 Distanta dintre doua drepte a si b, necoplanare in spatiu, reprezinta drumul minim de la un punct oarecare al dreptei a la un punct oarecare al dreptei b.

Probleme generale

1. Pe planul unui patrat ABCD se ridica de aceeasi parte perpendicularele AM si CP. Aflati drumul minim de la M la P daca , AM=2cm si CP=8cm.

Solutie

Construind inaltimea ME, EIPC se obtine dreptunghiul ACEM,

de unde si PE = PC - EC = 6cm.

Prin aplicarea teoremei lui Pitagora in triunghiul dreptunghic

PEM se obtine d(M; P) = MP = 10cm.

2. Pe planul unui patrat ABCD se ridica de-o parte si de alta perpendicularele AM si CP. Aflati drumul minim de la M la P daca , AM=2cm si CP=8cm.

Solutie

Prelungim segmentul (PC) cu segmentul (CE)s(AM)

si in acest caz AMCE devine dreptunghi, deci CE = AM = 2cm,

si m(<CEM) = 90^o.

Prin aplicarea teoremei lui Pitagora in triunghiul dreptunghic

PEM se obtine d(M; P) = MP =cm

3. Pe planul unui romb ABCD, cu si m(<ABC)=120^o se ridica perpendiculara AS, cu AS=9cm. Daca M si P sunt doua puncte situate pe dreptele SC, respectiv BD calculati distanta minima dintre M si P.

Solutie

Construim PM SC, MI SC

Daca P₁IBD, cu P₁ P atunci DMPP₁ dr. in P, deci MP<MP₁.

Daca M₁ISC, cu M₁ M atunci DPMM₁ dr. in M, deci MP<PM₁.

In concluzie d(BD; SC) = MP.

Prin aplicarea lui sin60^o in DAPB dr. in P se obtine AP = 6cm, de unde AC = 12cm.

Aplicind cazul de asemanare U.U. obtinem DSAC DPMC si de aici rezulta , deci d(BD; SC) = 3,6cm.

4. Pe planul unui romb ABCD, cu si m(<ABC)=120^o se ridica perpendiculara AM, cu AM=9cm. Daca P este un punct oarecare al dreptei MC calculati valoarea minima a ariei triunghiului BPD.

Solutie

Construim OP MC, PI MC

si in acest caz

PO este cea mai scurta inaltime a triunghiului BPD.

Deci (am utilizat rezultatele numerice de la problema 3).

Aplicatii ale problemelor generale pe poliedrele studiate

5. Fie ABCDA'B'C'D' o prisma patrulatera regulata cu si AA'=8cm. Daca M este un punct situat pe dreapta A C, calculati valoarea minima a ariei triunghiului BMD.

Solutie

Construim PM A'C, MI A'C

si in acest caz

MP este cea mai scurta inaltime a triunghiului BMD.

Aplicind cazul de asemanare U.U. obtinem DPMC DA'AC si de aici rezulta .

Deci .

6. Fie VABC o piramida triunghiulara regulata cu si inaltimea VO=8cm. Daca M si P sunt doua puncte situate pe dreptele BC, respectiv VA calculati distanta minima dintre M si P.

Solutie

Consideram M mijlocul muchiei (BC)

Deci (VM) mediana si inaltime in DVBC isoscel cu baza (BC)

si (AM) mediana si inaltime in DABC echilateral.

In acest caz avem:

Construim MP VA, PI VA

Realizand un rationament similar cu cel din problema 3 deducem ca

distanta minima dintre M si P se obtine in situatia de perpendicularitate a dreptei

MP pe dreptele BC, respectiv VA.

Prin aplicarea proprietatilor triunghiului echilateral ABC obtinem AM = 9cm si AO = 6cm.

Aplicand teorema lui Pitagora in DVOA obtinem VA = 10cm.

Exprimand aria triunghiului VAM in doua moduri obtinem min(MP) = 7,2cm.

7. Fie VABCD o piramida patrulatera regulata cu si inaltimea VO=8cm. Daca M este un punct situat pe muchia (VA) calculati valoarea minima a ariei triunghiului BMD.

Solutie

Construim OM VA, MIVA

si

in acest caz MO este cea mai scurta innaltime

a triunghiului BMD.

Deci ,

unde MO s-a calculat ca inaltime in triunghiul

VOA dreptunghic in O.

8. Fie ABCDA'B'C'D' o prisma patrulatera regulata cu AB=4cm si AA'=6cm. O furnica porneste pe suprafata laterala din A spre C alegand drumul minim. Calculati lungimea acestui drum minim.

Solutie

Drumul minim al furnicii este drumul in linie dreapta pe desfasurarea suprafetei laterale. Deci prin aplicarea teoremei lui Pitagora in DACC se obtine AC' = 10cm.

9. Fie ABCDEFA'B'C'D'E'F' o prisma hexagonala regulata cu AB=4cm si AA'=9cm. O furnica porneste pe suprafata laterala din A spre D alegand drumul minim. Calculati lungimea acestui drum minim.

Solutie

Drumul minim al furnicii este drumul in linie dreapta pe desfasurarea suprafetei laterale. Deci prin aplicarea teoremei lui Pitagora in DADD se obtine AD = 15cm.

10. Piramida hexagonala regulata VABCDEF are muchia laterala de si masura unghiului AVB de 30^o. O furnica porneste pe suprafata laterala din A in D alegand drumul minim. Calculati acest minim.

Solutie

Drumul minim al furnicii este drumul in linie dreapta pe desfasurarea suprafetei laterale. Se deduce ca DAVD este dreptunghic si isoscel si prin aplicarea teoremei lui Pitagora se obtine AD = 20cm.

Bibliografie

M. Radu "MATEMATICA-Manual pentru clasa a VIII-a"

A. Negrila si M. Negrila "Mate 2000" Paralela 45

P. Boldea, Z. Blajovan, C. Bociu si altii "Matematica impreuna" Waldpress