INTERDISCIPLINARITATEA

interdisciplinaritateA

modalitATi de asigurare a corelaTiei interdisciplinare Intre obiectele

matematicA-chimie-fizicA -biologie-informaticA

cuprins

1.iNTRODUCERE

2.iNVtAREA INTERDISCIPLINAR

3.VIZIUNEA INTERDISCIPLINARA

ASUPRA EDUCATIEI

4.MODALITATI DE ASIGURARE A

CORELATIEI INTERDISCIPLINARE

INTRE DISCIPLINELE:

matematicA-chimie-fizicA-biologie-informatiCA (TEME CU CARACTER INTERDISCIPLINAR)

Motto: ''Educatia are dificila misiune de a transmite o culturA acumulatA de secole, dar Si o pregAtire faTA de un viitor, In bunA mAsurA, imprevizibil''

JACQUES DELORS

Introducere

In mod firesc, omul gandeste interdisciplinar. De altfel, practica sociala nici nu cunoaste probleme unidisciplinare, dimpotriva, ea reclama-pentru adecvarea demersurilor teoretice-deschiderea si comprehensiunea spre si pentru toate domeniile cunoasterii.

Infaptuirea acestui deziderat este cu atat mai stringent cu cat astzi nu se mai poate concepe solutionarea corespunztoare a unei probleme fr a tine seama de toate laturile gandirii stiintifice, de imbinarea tuturor domeniilor cunoasterii intr-un tot unitar.

Prin tendintele ce se manifest in evolutia invtmantului contemporan, fr indoial c interdisciplinaritatea constituie una din cele care s-au impus cel mai mult atentiei. Problematica pe care o genereaz acest mod de abordare a fenomenelor lumii obiective se extinde, logic si necesar, si asupra modului in care se realizeaz studiul acestora in contextul activittii scolare. Cu alte cuvinte, interdisciplinaritatea -devenit in mod necesar o modalitate nou de gandire si actiune, izvorat din cerinta identificrii, analizei, sintezei, definirii, deci a cunoasterii conexiunilor dintre obiectele si fenomenele lumii reale- se impune ca una din directiile principale ale renovrii activittii in invtmant in ansamblul su si mai ales a continutului acesteia si a strategiilor de lucru aplicate.

-interdisciplinaritatea este o conditie si premis a 'pertinentei' continuturilor in raport cu problematica lumii contemporane, cu mutatiile din sfera culturii, a stiintelor, a cercetrii stintifice fundamentale si aplicative, a profesiilor;

-cunostiintele realizate de cursanti in conditiile organizrii traditionale a cunostintelor, preponderent monodisciplinar, se constituiau intr-un ansamblu de fenomene izolate, ce generau o viziune linear si static asupra lumii, in contradictie cu marea varietate si dinamismul feneomenelor reale;

-interdisciplinaritatea ofer imaginea domeniilor de cunoastere permanent deschise completrilor si restructurrilor, studiul lor vizeaz continuu noi tipuri de formare si specializare in cadrul inovrii structurrilor si metodologiei didactice;

-interdisciplinaritatea permite valorificarea larg a informatiilor dobandite de elevi pe alte filiere decat cele scolare si transformarea lor in structuri cognitive;

-interdisciplinaritatea este un reflex si o modalitate de raportare la 'revolutia informational';

-favorizand transferurile intre domeniile de cunoastere si de la acestea la actiune, de asumare a unui stil de viat eficient;

-Interdisciplinaritatea implica un anumit grad de integrare intre domenii de cunoastere, diferite abordari si utilizarea unui limbaj comun, promitand schimbari de ordin conceptual si metodologic. Ca perspectiva de organizare a continuturilor, interdisciplinaritatea provoaca elevii sa se familiarizeze si sa opereze cu principii sau concepte generale si orientate in contexte cognitive diferite.

-Intradisciplinaritatea sau monodisciplinaritatea reprezinta forma traditionala de instruire. Principalul avantaj este acela ca securizeaza elevul in avansarea sa riguroasa si gradual ascendenta pe un traseu cognitiv dat.

-Multidisciplanaritatea reprezinta forma cea mai putin dezvoltata a transferurilor disciplinare, realizandu-se de cele mai multe ori prin juxtapunerea anumitor elemente ale diverselor domenii, in scopul reliefarii aspectelor lor comune.

Pluridisciplinaritatea propune o perspectiva tematica. Punctul de pornire al structurii continuturilor il reprezinta o tema, situatie, problema, abordata de mai multe discipline, cu metodologii specifice. Prezinta avantajul abordarii unui fenomen in globalitatea sa, in contextul multiplelor sale relatii cu alte fenomene din realitate.

Transdisciplinaritatea poate fi definita ca :

intrepratrunderea mai multor discipline coordonate cercetarii a.i. pot conduce la constituirea unei noi discipline sau a unui nou domeniu de cunoastere. Este o acceptiune foarte apropiata conceptului de interdisciplinaritate, cu care, dealtfel se confunda adeseori; sau o noua abordare a domeniilor de cunoastere din invatamant, centrata nu pe domenii, discipline, obiecte.

2 Invatarea interdisciplinara-conditie a modernizarii

Predarea-invatarea optima reclama din partea fiecarui educator cunoasterea disciplinelor din planul de invatamant, evident a domeniilor, partilor, notiunilor, judecatilor si rationamentelor adiacente intelegerii cunoasterii si invatarii in conditii firesti a stiintei respective.

Renuntarea la predarea-invatarea monodisciplinara si trecerea la cea interdisciplinara a fost, este si va fi rezultatul colaborarii, asa cum au fost si sunt consecinta ei mai toate rezultatele spectaculoase

obtinute in domeniul cercetarii.

3.Viziunea interdisciplinara asupra educatiei

In stiinta educatiei contemporane se impune cu tot mai multa insistenta conceptia interdisciplinara in c ercetarea si interpretarea fenomenului educational.

Fara a fi o simpla fuziune a rezultatelor obtinute in cadrul diverselor discipline care se ocupa de educatie, aceasta viziune interdisciplinara presupune valorificarea acestor rezultate prin elaborarea unei sinteze calitativ superioare privitoare la educatie in ansamblul sau, precum si la diferite aspecte concrete ale ei.

Interdisciplinaritatea presupune depasirea unor granite, eliminarea unor cadre rigide, ca domenii exclusive ale unei discipline, transferul de rezultate de la o disciplina la alta in vederea unei explicari mai profunde a fenomenelor, realizandu-se astfel o coordonare a diverselor unghiuri de vedere in locul predominarii unuia dintre ele, situatie care poate duce la o imagine unilaterala asupra educatiei si implicit la restrangerea rolului sau insocietate.

4.Modalitati de asigurare a corelatiei interdisciplinare intre disciplinele: matematica, fizica, chimie, biologie, informatica.

Cerinte imperioase ale dezvoltarii stiintei si tehnicii contemporane impun interdisciplinaritatea ca o modalitate eficienta de intelegere si integrare a cunostiintelor.

Realizarea corelatiei interdisciplinare intre matematica-fizica-chimie-biologie-informatica, discipline fundamentale, constituie o necesitate obiectiva ca urmare a interferarii domeniilor; in caz contrar, privam elevul de o viziune unitara asupra naturii si de o reflectare si intelegere exacta a acesteia.

Ca urmare, in studiul unui obiect de invatamant , abordarea interdisciplinara presupune un mod de a gandi si actiona care s-ar putea sistematiza in urmatoarele etape:

I).Sesizarea cunostintelor din domenii diferite care sa interfereze cu OBIECTUL RESPECTIV printr-un studiu atent si interrelat.

Sub acest unghi de vedere s-ar putea stabili ca obiecte mai mult sau mai putin apropiate: matematica, chimia, fizica, biologia, informatica.

In aceasta idee corelatia matematica-chimie se poate realiza prin utilizarea algoritmilor matematici in rezolvarea problemelor de chimie. Astfel, pentru determinarea concentratiei unei solutii clasele a VII-a se aplica algoritmul invatat la matematica in clasa a VII-a la capitolul 'Probleme de amestecuri si aliaje". Tot pentru a stabili compozitia unui amestec se aplica algoritmul de rezolvare a unui sistem de ecuatii.

Exemplu: Trebuie explicat elevului notiunea de amestec, acesta fiind o asociere de mai multe corpuri, obiecte, materiale, produse fara ca intre ele sa existe o reactie chimica. Amestecurile sunt rezultatul curiozitatii oamenilor, ele avand ca scop corijarea anumitor proprietati diferite de cele ale elementelor introduse in ansamblu

﴾ concentratie, titlu, densitate, temperatura, pret de cost, etc. ﴿

A O problema de acest gen poate fi enuntata astfel: Intr-un laborator exista solutii de acid sulfuric de concentratie 90% si 70%. Ce cantitati dintre cele doua solutii amestecam pentru a obtine 500g de solutie de acid sulfuric cu concentratia de 72%?

Se calculeaza ajutandu-ne de media ponderata a proprietatii amestecului, astfel se realizeaza un sistem de ecuatii in x si y, unde acestea sunt cantitatile de solutie de acid sulfuric de 90% si respectiv 70%:

72%=

500=x+y

Se rezolva sistemul in necunoscutele x si y si obtinem:

x=50g sol. 90% si y=450g sol. 70%.

B) O alta problema cu legatura intre disciplinele matematica-chimie este cea a aliajelor care este tot o problema de amestec, specificand faptul ca aliajele sunt amestecuri de mai multe metale topite impreuna. Aliajele in care intra metale pretioase se numesc metale fine, iar aliajul are un <titlu> definit prin raportul: t=Gt/Gm Gt este greutatea totala a alijului si Gm este greutatea metalului pretios continut.

Ex. Cat cupru, ρ=8,9kg/dm³ si cat cositor cu ρ=7,2kg/dm³ contine o bucata de bronz cu masa de 50 kg si volumul de 6 cm³ ?

Rezolvarea se face folosind tot un sistem de ecuatii in care notam cu x si y masa in kg a cuprului respectiv a cositorului. Astfel, folosind si relatia intre m-V- ρ, obtinem v olumul cuprului in bucata de bronz este x/8,6 si a cositorului y/7,2.

Avem sistemul :

x/8,6+y/7,2=6

x+y=50

cu solutiile : x-35,6kg Cu, y=14,4kg cositor.

II).Stabilirea cuantumului de cunostinte ale obiectului, pentru o anumita clasa si in raport cu particularitatile de varsta ale elevilor si cu nivelul acestora.

De exemplu, electroliza ca fenomen se studiaza in clasa a VI-a la fizica, apoi aplicatiile electrolizei in vederea obtinerii oxigenului si hidrogenului, in clasa a VIII-a la chimie.

O problema destul de importanta cu multe aplicatii practice, in cadrul algebrei, este aceea referitoare la notiunea de functie. Aceasta notiune fundamentala in matematica trebuie sa apara de la inceput ca o corespondenta intre doua multimi. Astfel se va arata ca se va ajunge la studiul unei functii liniare, considerand: lungimea cercului fata de diametru, spatiul in raport cu timpul, cand viteza este constanta, dependenta intre viteza si timp la o miscare uniform acdelerata, legatura intre volum si temperatura la presiune constanta sau aceea dintre presiune si temperatura la un volum constant, lungimea unei bare fata de temperatura la care este incalzita, etc.

III).Cuprinderea intr-o viziune unitara, integratoare a diverselor cunostinte de matematica, fizica, chimie, biologie, informatica in scopul cunoasterii si intelegerii realitatii investigate in cadrul procesului de invatamant. Precizarea structurii sau a structurilor corespunzatoare pentru cuprinderea intr-o viziune unitara a cunostintelor interrelate.

Exemplificare:

Formarea imaginii unui obiect printr-o lentila, folosind cunostinte de fizica, matematica si informatica, concretizand prin formarea imaginii pe retina biologie

a﴿Formarea imaginii unui obiect intr-o lentila, deducerea FORMULEI LENTILELOR utilizand metoda asemanarii triunghiurilor

sunt necesare cunostinte de fizica, geometrie, algebra

Pozitia imaginii unui obiect depinde atat de distanta obiect-lentila p cat si de distanta focala f a lentilei. Matematic se poate demonstra ca distanta lentila-imagine p^, este data de relatia:

-1/p+1/p`=1/f (formula lentilelor) à 1/p<sup>`</sup>=1/f+1/p

In aplicarea acestei relatii se foloseste urmatoarea conventie de semne:

p=negativ

f=pozitiv pt. Lentile convergente

f=negativ pentru lentile divergente

p`=pozitiv daca imaginea este reala

p=negativ daca imaginea este virtuala

Utilizarea asemanarii triunghiurilor in demonstratia legii lentilelor

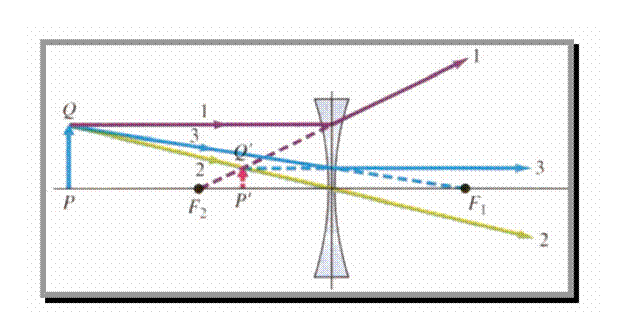
Demonstrarea legii lentilelor

Din constructia imaginii prin lentila identificam triunghiurile asemenea (doua triunghiuri care au unghiurile congruente). In triunghiurile asemenea laturile corespunzatoare unghiurilor congruente sunt proportionale. Triunghiurile OQP si OQ^'P^` sunt asemenea deoarece:

QOP si Q'OP^{`</sup> (opuse la varf) QOP= Q'OP<sup>`} (90^o

Rapoartele de proportionalitate ale laturilor: Q/P = Q'/P'  

Triunghiurile OIF² Si F² Q'Psunt asemenea, deci: OI/ Q'P' = F₂0/F₂P'

Dar IO=QP, deci din si ÞQP / Q'P'^{`</sup> = OP/OP<sup>`} =F₂O/F₂P'

Tinand cont de notatiile din figura :

lpl/p =f/p^{`</sup>-f Þ -p/p<sup>`} =f/p^`-f (3)

Facand produsul mezilor si al extremilor: p^`f=-p+p^,f / : (-pp^,f)Þ

-1/p+1/p^,=1/f (formula lentilelor).

c)Utilizarea unui minicalculator pentru a determina valoarea lui p^, (distanta lentila-imagine)

-tastati valoarea lui f : calculatorul memoreaza aceasta valoare;

-apasati tasta 1/x : calculatorul afiseaza inversul lui f ;

-apasati pe tasta -: calculatorul memoreaza operatia de scadere;

-tastati valoarea lui lpl: calculatorul memoreaza aceasta valoare;

-apasati tasta 1/x: calculatorul afiseaza inversul lui p;

-apasati pe tasta =:calculatorul efectueaza 1/f+1/p si valoarea lui 1/p^,

-apasati pe tasta 1/x:calculatorul va afisa valoare lui p^,.

Observatie: in cazul unui minicalculator care nu are tasta 1/x atunci se tasteaza in ordine: 1;:; valoarea lui f; M⁺;1;:;R.CM;;=.

d)Formarea imaginii pe retina (integrarea cunostintelor de biologie-fizica-matematica).

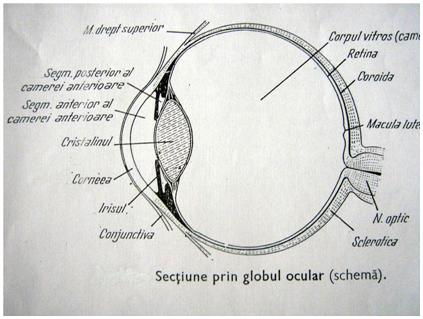
Razele luminoase care vin de la o sursa luminoasa sau luminata (raze reflectate pe suprafata unui obiect) strabat prin mediile transparente (cornee, umoare apoasa, cristalin, umoare sticloasa) si ajung pe retina. Mediile transparente constituie un sistem dioptric, in care razele se refracta (mediu refringent) si se concentreaza (mediu convergent) intr-un focar pe retina, determinandformarea unei imagini reale, mai mica si rasturnata. Razele de lumina sufera o tripla refractie :

1.cand trec din aer in cornee,

2.cand trec din umoarea apoasa pe fata anterioara a cristalinului,

3.cand trec de pe fata posterioara a cristalinului in corpul vitros.

Sistemul dioptric al ochiului normal poseda o astfel de putere de refractie, incat razele luminoase care vin de la o sursa indepartata si cad paralel asupra corneei, se focalizeaza la o distanta de 24 mm inapoia corneei, adica pe retina. In acest caz ochiul este emertrop.

Cand puterea de refractie a sistemului dioptric este slaba si prin aceasta si puterea de convergenta a sistemului este mai redusa, sau daca axul anteroposterior al ochiului estemai mic, razele paralele se concentreaza inapoia retinei. Avem de-a face cu un defect al vederii, numit hipermetropie. Pentru corectare se folosesc ochelari cu lentile convergente (biconvexe), care aduna razele intr-un fascicul convergent, centrat pe retina, unde se stabileste focarul sau e indepartat obiectul.

Cand ochiul are un sistem dioptric cu o prea mare putere de refractie, datorita unei prea mari curburi a corneei, si o prea mare capacitate convergenta sau cand ochiul este alungit inapoi si astfel retina este indepartata, focalizarea razelor nu se mai poate face pe retina, ci inaintea ei. Acest defect al ochiului se numeste miopie. Pentru a mari distanta focala a razelor refractate se folosesc lentile divergente biconcave de valoare identica cu gradul miopiei, care readuc focarul pe retina, sau apropie obiectul.

Astigmatismul este tot un defect al ochiului si se datoreaza faptului ca corneea nu este uniforma, ci prezinta defecte de sericitate; in acest caz, razele se focalizeaza in mai multe puncte pe retina. Se corecteaza cu ochelari ale caror lentile sunt cilindrice si egalizeaza refractia pe toate meridianele.

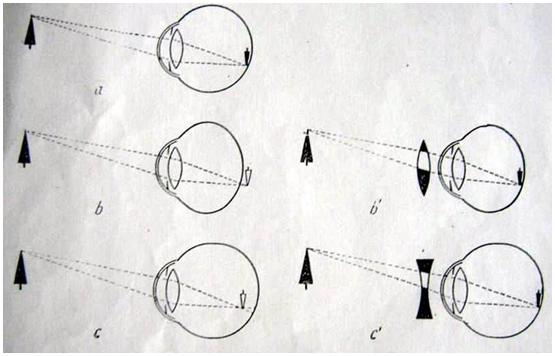
Formarea imaginii pe retina:

a-ochi emertrop; b-ochi hipermetrop; b1-corectarea prin lentila convergenta; c-ochi miop; c1-corectarea prin lentila divergenta.

4.Determinarea metodologiei specifice procesului de cunoastere implicat de tema propusa, fie specifica obiectului, fie importata-prin transfer-de la diferite discipline tangente.

Lectiile de chimie si fizica bazate pe rezolvari de probleme presupun realizarea permanenta a corelatiei chimie-fizica-matematica, prin aplicarea proprietatilor proportiilor, rezolvarea ecuatiilor de gradul I si II, reprezentarea grafica a unei functii, etc.

Exemple:

I O problema abordata interdisciplinar de profesorul de matematica si fizica este tema ''Compunerea fortelor concurente''care cere, sa se determine valoarea rezultantei a doua forte concurente perpendiculare. Pentru aceasta este nevoie sa se aplice Teorema lui Pitagora studiata la geometrie.

Aceasta problema, abordata interdisciplinar capata o dubla valoare: pe de o parte teorema va fi prezentata ca fapt stabilit experimental apartinand fizicii, pe de alta parte matematica o va utiliza ca exemplu pentru intelegerea unor lucrari abstracte.

Sefectueaza experimentul din figura:

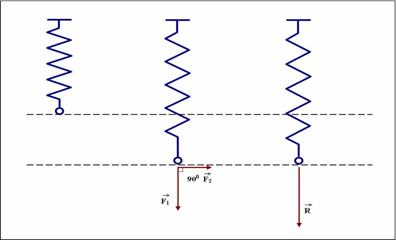
Mentinand unghiul dintre cele doua forte de 90⁰, se modifica valorile pentru fortele F₁ si F₂. La fiecare valoare noua pentru aceste forte, se procedeaza la o inlocuire a acestora prin singura forta r care sa produca aceeasi deformare a resortului. Se repeta seria masuratorilor si rezultatele se trec intr-un tabel.

Se ajunge la concluzia ca pentru doua forte concurente perpendiculare F₁ si F₂ valoarea rezultantei R se determina prin relatia legea lui Pitagora:

R²=F₁²+F₂²

^{Se poate aminti elevilor despre Pitagora - c. 580 i.Hr. - c.500 i.Hr.) a fost un filozof si matematician grec, originar din insula Samos, NUMERELE GUVERNEAZA LUMEA! - era scris pe frontispiciul Scolii Pitagoreice
  La inceput a fost numarul  a spus Pitagora}

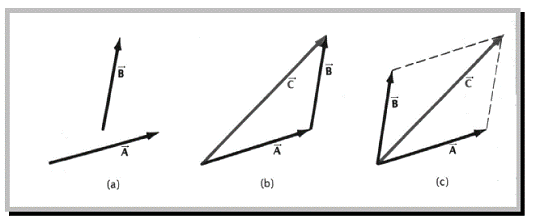
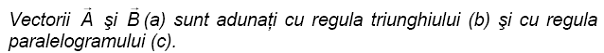
Procedand astfel, profesorul de fizica a pus la indemana elevilor doua metode de a gasi rezultanta a doua forte concurente perpendiculare: grafic, cu regula paralelogramului si prin calcul cu ajutorul legii lui Pitagora. Este de la sine inteles ca, abordata interdisciplinar de catre profesorul de matematica, chestiunea in cauza capata profunzime.

II In cazul interferentei chimie-matematica gasim o problema de tipul

Stabiliti coeficientii chimici pentru urmatoarea ecuatie chimica:

FeS₂+O₂=Fe₂+SO₃

Rezolvarea se face scriindu-se coeficientii ecuatiei chimice sub forma de necunoscute, se pune problema in ecuatie pe baza conservarii numarului de atomi intr-o reactie chimica, se obtine un sistem care se rezolva, solutiile reprezentand chiar coeficientii chimici.

xFeS2+yO2=zFe2O +uSO3

n     x=2z

n     2x=u

n     2y=3z+2u

n     pt x=1 rezulta z=1/2; u=2si y=11/4

n     pentru a obtine coeficienti naturali inmultim cu 4 si rezulta astfel ecuatia cu urmatorii coeficienti:

4FeS2+11O2=2Fe2O +8SO3

III In cazul problemelor de miscare, s-au stabilit legaturi armonioase intre durata, distanta si viteza.

D.p.d.v. matematic pentru un mobil in miscare uniforma, durata traseului t si distanta parcursa d, sunt marimi proportionale, coeficientul de proportionalitate fiind viteza, notata uzual cu v. Astfel, viteza unui mobil este distanta parcursa in unitatea de timp.

Aceste relatii se aplica in cadrul problemelor de fizica ce au ca cerinta distanta parcursa de un mobil intr-un anume interval de timp, cu ajutorul unui tabel de proportionalitate intre marimi.

O aplicatie a matematicii este de a reprezenta grafic obiecte care sunt prea mari sau prea mici pentru a fi reprezentate in dimensiunile reale. S-a convenit ca dimensiunile lor sa fie reduse sau marite respectand o proportionalitate intre dimensiunile reale si cele reproduse. Planurile si hartile sunt aplicatii ale rapoartelor si proportiilor.

Coeficientul de proportionalitate dintre dimensiunile unui obiect reproduse printr-un plan, desen, fotografie, macheta, harta si cele reale se numeste scara.

Oproblema pe care o putem aplica si in cadrul orei de geografie este aceea de a calcula distanta care separa doua orase avand o harta cu o anumita scara de reproducere (ex.1:1700000).

IV)In cadrul lectiei'' Mecanisme simple-parghiile''se poate vorbi de ''

Parghiile din organism si importanta lor''-punandu-se in evidenta interferenta fizica-biologie

De la biologie se stie ca

-totalitatea oaselor din organism reprezinta sistemul osos sau scheletul ;

-forma oaselor este determinata de rolul pe care il indeplinesc in organism;

-oasele pot avea rol de sustinere a corpului si in aceasta categorie intra coloana vertebrala (care sustine greutatea tuturor organelor) si oasele membrelor inferioare ( care sustin greutatea corpului); alte oase au rol de protectie pentru diferite organe, deoarece marginesc unele cavitati care adapostesc organele interne (oasele cutiei craniene, vertebrele, coastele, sternul); sunt si oase cu rol in miscarile corpului, constituind organe pasive (puncte de insertie ale muschilor);

-in functia pasiva oasele joaca rol de parghii.

De la fizica se stie ca 

-parghia este un mecanism simplu care serveste la transmiterea fortelor si a miscarilor de la elementul conducator la elementul condus ;

-parghia este o bara rigida care se poate roti in jurul punctului de sprijin si asupra careia actioneaza doua forte : forta care trebuie invinsa, numita forta rezistenta (R) si forta care determina actiunea, numita forta activa (F) ;

-dupa raportul dintr punctul de aplicatie al fortei (reprezentat prin muschi) s al rezistentei (reprezentar prin greutatea deplasata), parghiile osoase se pot grupa in cele trei categorii cunoscute in mecanica :

1.Pirghia de gradul I

Punctul de sprijin se gaseste intre punctul de aplicatie al fortei active si cel al fortei rezistente (R-S-F)

S

O asemenea parghie este realizata la mentinerea capului in echilibru pe coloana vertebrala ; punctul de sprijin se afla la articulatia capului cu coloana, forta F este in muschii cefei, iar rezistenta este data de greutatea fetei.

2.Parghia de gradul II

Forta rezistenta se afla intre punctul de aplicatie al fortei F si punctul de sprijin (S-R-F)

S

O asemenea parghie este realizata la ridicarea corpului pe varful picioarelor: punctul de sprijin este la varful piciorului, punctul de aplicatie al rezistentei la articulatia oaselor gambei cu oasele tarsiene si forta activa se aplica pe osul calcaiului. Este parghia realizata in timpul mersului.

3.Parghia de gradul III

Are forta activa intre punctul de sprijin si punctul de aplicatie al fortei rezistente (S-F-R).

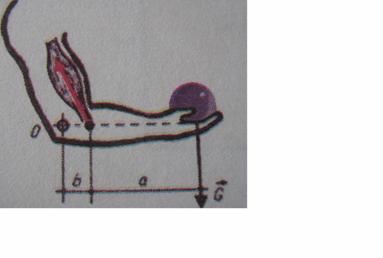
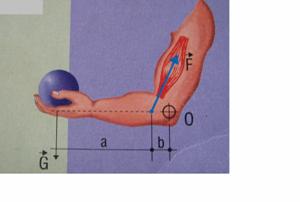
O asemenea parghie se realizeaza la membrul superior in timpul ridicarii unei greutati asezata in palma prin flexia antebratului pe brat: rezistenta se afla in palma, punctul de sprijin in articulatia cotului, punctul de aplicatie al fortei pe oasele antebratului.

Acest tip de parghie se realizeaza si la articulatia umarului si genunchiului.

Activitatea sportiva de performanta impune pe langa o activitate musculara crescuta si o coordonare a miscarii sistemului osos pentru precizia miscarii:

-in gimnastica ritmica si in balet, precizia si rafinamentul miscarilor in coordonarea scheletului, primeaza fata de activitatea musculara;

-miscarile coordonate ale diferitelor grupe musculare stau la baza performantelor actorilor in gestica si mimica;

-muzicienii (pian, vioara, violoncel) isi pun in valoare toate parghiile degetelor si ale bratelor, antrenand grupele de muschi corespunzatoare pentru a da tonalitatea melodica;

-sculptorii, cioplitorii in piatra, in mod deosebit, imbina forta musculara cu coordonarea miscarilor parghiilor osoase.

EMINESCU SI FIZICA

Virtutile curiozitatii au facut ca un mare poet al culturii noastre sa fie puternic atras de cunostintele stiintifice ale timpului sau, aceasta devenind uneori chiar izvor al propriei creatii.

La steaua

La steaua care-a rasarit

E-o cale atat de lunga,

Ca mii de ani i-au trebuit

Luminii sa ne -ajunga.

Poate de mult s-a stins din drum

In departari albastre,

Iar raza ei abia acum

Luci vederii noastre..

Eminescu detinea informatii cu privire

la viteza luminii c= 3●108 m/s si a imbinat

armonios aceste cunostinte.

Studiile facute la Viena si Berlin l-au apropiat pe Eminescu de operele unor nume cunoscute si recunoscute ale stiintei -Arhimede, Galileo Galilei ,Johannes Kepler,Isaac Newton ,Daniel Bernoulli, Chales de Coulumb, Brown, Robert von Mayer,James Loule,Hermsann von Helmholtz,Rudolf Clausius etc. familiarizindu-l totodata cu teoriile stiintifice ale momentului. In sprijinul acestei afirmatii stau nu numai poemele sale, ci si insemnarile referitoare la chestiuni legate de Fizica , insemnari cuprinse de doua caiete numite de Eminescu FIZIOLOGIE I si FIZIOLOGIE II .

Manuscrisele eminesciene impresioneaza prin variantele domeniilor abordate,dar si prin gradul de elaborare a informatiei stiintifice cele mai ample desfasurari avind insemnari referitoare la matematica si fizica.

MATEMATICIANUL DAN BARBILIAN

SI

POETUL ION BARBU

In cultura romaneasca, Dan Barbilian si-a facut aparitia intai ca poet si pe urma ca matematician. In anul 1919, Dan Barbilian s-a prezentat la locuinta lui Eugen Lovinescu, criticul si istoriograful literar, cu primele sale poezii semnate Popescu. Lovinescu i-a atras atentia cu privire la raspandirea numeleui, si ii propune, ca pseudonim numele bunicului sau, Ion Barbu. Dupa 1930 insa s-a consacrat exclusiv matematicii impunandu-se prin creatiile sale de geometrie si algebra.

n     "A face geometrie , fara a -l pomeni pe Euclid este la fel cum ai juca piesa Hamlet, fara Hamlet"

n     A.N. Whitehead - matematician englez

n    

n     M-au interesat Dialogurile lui Platon, dar trebuie sa marturisesc ca asez mai presus de ele postulatele lui Euclid pe care le-am parcurs tot atunci, adica in anii formarii mele intelectuale

n     'Geometrii folosesc figuri vizibile si judeca pe ele, dar ei nu se gandesc la aceste figuri, ci la altele, cu care seamana, dar care nu pot fi vazute decat in minte'.

n     ..In univers urla un punct / de durerea unui cerc / care-l inconjoara' (Spirit de haiku).

n     Ca sa te indoiesti de linia dreapta / trebuie sa stii mai intai din cate puncte / e facuta

Euclid din Alexandria
n. 325 - m. 265 I. Chr

n     Supranumit de urmasi "parintele geometriei" , Euclid a fost primul care a reusit sa defineasca aceste notiuni abstracte punctul, dreapta, planul

n     Punctul este ceva ce nu are nici o parte.

n     Linia este lungime fara latime.

n     Dreapta este linia la fel situata fata de toate punctele ei.

n     Planul este suprafata situata la fel fata de toate dreptele continute.

In cele expuse, din exemplele date, reiese ca profesorul, indiferent de disciplina pe care o preda, poate si trebuie sa realizeze interdisciplinaritatea, sa aiba o conceptie interrelata asupra fenomenelor, in situatiile in care formatia si perfectionarea sa ulterioara s-au realizat pe baza unei viziuni unitare. Numai astfel el va putea actiona corespunzator pe linia formarii unei conceptii stiintifice despre lume si viata, pe linia intaririi caracterului instrumental, operational si in acelasi timp functional al cunostintelor pe linia cresterii randamentului scolar.

Bibliografie:

1.Sinteze din UNESCO, 1986, ''Interdisciplinaritatea si stiintele umane'', colectia ''Idei contemporane'', Bucuresti, Raport UNESCO, 1985, ''Interdisciplinaritate''. Coherence et Equilibre des contenus de l'enseignement general, Paris si Simpozion, 1983, ''Stefan Odobeja'', Iasi.

2.I. Neacsu, 1983, ''Invatamantul modular-strategie integrata in abordarea interdisciplinara a invatamantului'' Revista de pedagogie nr.3.

3Ioan Nicola, ''Pedagogie''E.D.P.P.A.-Bucuresti 1994.

4.Stefan Milcu, ''Despre geneza stiintelor multi- si interdisciplinare'' in interdisciplinaritatea contemporana'' E.D.P., 1980, Bucuresti.

5.Ioan Cerghit, ''Abordarea sistematica si implicatiile ei asupra optimizarii lectiei'' Revista de pedagogie nr.4, 1989.

6. Transdisciplinaritate -Manifest , de Basarab Nicolescu-Editura Polirom-Iași.

7. Implementarea tehnologiilor in educație sau educație tehnologica -prof.univ. dr. Vasile Marcu.

8. Omul-sistem fizico-chimic și biologic deschis -Maria-Mihaela Pațica, Iuliana-Antoanela Pațica.