Probleme Fizica

Probleme Fizica

Sa se precizeze forma ionica predominanta a acidului carbonic HCO intr-o solutie avand pH = 5,5. Se dau pentru cele doua trepte de disociere ale acidului: pK₁ = 6,4; pK₂ = 10,3.

Un recipient cu volumul de 100 mL contine o solutie apoasa cu m = 60 mg CHCOOH (M = 60 g/mol) si m = 164 mg CHCOONa (M = 82 g/mol). Sa se calculeze:

a.      concentratiile molare ale substantelor dizolvate;

b.     pH-ul solutiei, daca se cunoaste pentru acidul acetic pK = 4,7 si lg2 = 0,3;

c.     cat devine pH-ul daca la solutie se adauga m = 36,5 mg HCl (M = 36,5 g/mol)?

Fie doua compartimente A si B separate printr-o membrana permeabila doar pentru apa. Compartimentul A are volumul V_A = 200 mL si contine o solutie de HCl (M₁ = 36,5 g/mol) cu pH_A = 2 in care se afla dizolvate:

m₂ = 3,42 g Al₂ (SO₄)₃ (M₂ = 342 g/mol)

m₃ = 600 mg uree (M₃ = 60 g/mol).

Compartimentul B, de volum V_B = 500 mL contine:

m₄ = ? H₃PO₄ (M₄ = 98 g/mol) de concentratie c₄ = 4∙10 ^-2 M

m₅ = ? NaH₂PO₄ (M₅ = 120 g/mol) de concentratie c₅ = 2∙10 ^-2 M

Sa se determine:

a.          concentratia c₂ in mol/L;

b.         concentratia c₃ in mol/L;

c.         masa m₄ exprimata in g;

d.         masa m₅ exprimata in mg;

e.          masa m₁ exprimata in g;

f.           pH_B; pentru H₃PO₄ se dau pK₁ = 2,1; pK₂ = 7,2; pK₃ = 12,3; lg2 = 0,3;

g.         presiunile osmotice p_A si p_B in cele doua compartimente; prin ce mecanism, in ce directie si cu ce presiune strabat moleculele de solvent membrana ce separa compartimentele? Se da R T = 25 L atm/mol;

h.         ce volum de apa trebuie adaugat in compartimentul A pentru a modifica pH - ul cu 1 unitate ? Dar in compartimentul B?

In atomul de hidrogen protonul si electronul se gasesc la o distanta d = 5,3∙10^-11 m unul de altul. Cunoscand valoarea sarcinii electrice elementare e = 1,6∙10^-19 C si valoarea constantei lui Coulomb k = 9∙10⁹ N∙m² / C² sa se precizeze natura (atractie sau respingere) si sa se calculeze modulul fortei de interactiune electrostatica dintre cele doua particule.

Fie doua sarcini punctiforme q₁ = 3 μC si q₂ = 5 μC situate la distanta d = 3 m una de alta. La 1 m de sarcina mai mare se plaseaza o a treia sarcina punctiforma, coliniara cu celelalte doua si situata intre ele q₃ = - 1 μC. Sa se calculeze:

a) forta rezultanta ce actioneaza asupra sarcinii 3;

b) cu ce distanta si in ce sens va trebui deplasata sarcina 3 pentru a se gasi in echilibru ?

Se neglijeaza forta de greutate si se da constanta lui Coulomb k = 9∙10⁹ N∙m² / C².

Doua sarcini electrice punctiforme q₁ si q₂ aflate la distanta de 50 cm una de alta se resping cu o forta de 25 μN. Sa se calculeze valoarea fortei de interactiune daca reducem la jumatate distanta dintre sarcini. Se da constanta lui Coulomb k = 9∙10⁹ N∙m² / C².

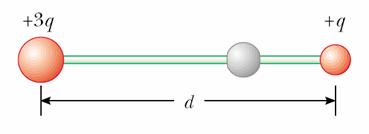
Doua bile metalice de mici dimensiuni avand sarcinile 3q si q sunt fixate la capetele unei tije de sticla de lungime d (vezi Figura). Pe tija culiseaza fara frecare o a treia bila avand sarcina - 3q. La ce distanta de sarcina 3q se va gasi aceasta in echilibru.

Trei sarcini punctiforme identice, fiecare avand q = 3 nC sunt situate in varfurile unui triunghi echilateral cu latura de 5 cm. Sa se calculeze forta rezultanta ce actioneaza asupra unei sarcini q' = - 1 nC plasate in centrul de greutate al triunghiului (punctul de intersectie al inaltimilor). Se da constanta lui Coulomb k = 9∙10⁹ N∙m² / C².

Sa se calculeze modulul intensitatii campului electric generat de o sarcina punctiforma q = 2∙10 ^-6 C intr-un punct situat la distanta de 10 m de aceasta. Sa se reprezinte liniile campului electric generat de sarcina, precizand si sensul lor. Se da constanta lui Coulomb k = 9∙10⁹ N∙m² / C².

Sa se precizeze sensul liniilor de camp si sa se calculeze modulul intensitatii campului electric uniform necesar pentru a echilibra forta de greutate a unui:

a) electron;

b) proton.

Se dau: masa electronului m_e = 9,1∙10^-31 kg, masa protonului m_p = 1,67∙10^-27 kg, sarcina electrica elementara e = 1,6∙10^-19 C, acceleratia gravitationala g = 10 N/kg si constanta lui Coulomb k = 9∙10⁹ N∙m² / C².

Patru sarcini punctiforme identice q = 2 μC sunt localizate in varfurile unui patrat cu latura de 20 cm. Sa se calculeze modulul intensitatii campului electric rezultant in:

a)     centrul patratului (punctul de intersectie al diagonalelor);

b) unul dintre varfurile patratului.

Se da constanta lui Coulomb k = 9∙10⁹ N∙m² / C².

Fie un dipol electric compus din sarcinile + q si - q avand axa orientata de-a lungul axei Ox (vezi Figura). Sarcina + q se afla in punctul de coordonata x = - a, iar sarcina - q, in punctul de coordonata x = + a (a > 0). Sa se deduca expresia modulului intensitatii campului electric rezultant in punctul de coordonata x = d (d > 0, d > a).

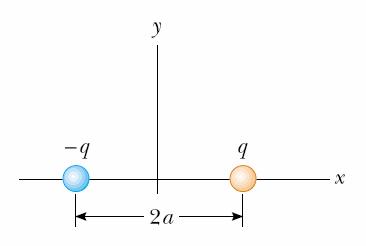
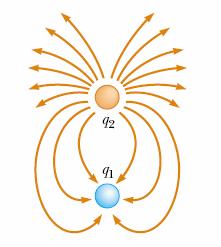
In Figura sunt prezentate liniile campului electric generat de sarcinile punctiforme q₁ si q₂ situate la mica distanta una de alta.

a) Sa se precizeze semnele sarcinilor;

b) Sa se afle valorile posibile ale raportului q₁ / q₂.

Un electron avand energia cinetica E_c intra intr-un camp electric uniform. Sa se precizeze directia, sensul si modulul intensitatii campului necesar pentru a incetini particula pana la oprire pe distanta d.

Un proton aflat initial in repaus se deplaseaza pe distanta d = 20 cm intr-un camp electric uniform de intensitate E = 5∙10⁴ N / C, de-a lungul liniilor de camp electric. Sa se calculeze:

a) forta electrica ce actioneaza asupra particulei;

b) acceleratia protonului;

c) viteza finala;

d) durata miscarii.

Se dau: masa protonului m_p = 1,67∙10^-27 kg, sarcina electrica elementara  e = 1,6∙10^-19 C, acceleratia gravitationala g = 10 N/kg si constanta lui Coulomb k = 9∙10⁹ N∙m² / C². Se neglijeaza forta de greutate.

Sa se calculeze potentialul electric generat de o sarcina punctiforma q = 5 μC intr-un punct situat la distanta r = 25 cm de sarcina.  Se da constanta lui Coulomb k = 9∙10⁹ N∙m² / C².

Sa se calculeze potentialul electric generat de un dipol electric format din sarcinile + q si - q unde q = 3 nC situate la distanta d = 6 cm una de alta in punctul:

a) situat la jumatatea distantei dintre sarcini si coliniar cu acestea;

b) situat la distanta r = 4 cm pe normala dusa pe axa dipolului in punctul situat la jumatatea distantei dintre sarcini.

Se da constanta lui Coulomb k = 9∙10⁹ N∙m² / C².

Doua sfere conductoare avand razele r₁ = 10 cm si r₂ = 5 cm sunt legate printr-un fir conductor (vezi Figura). Sferele sunt incarcate cu sarcinile q₁ = 2 μC si q₂ = ? uniform repartizate pe suprafata lor. Se da constanta lui Coulomb k = 9∙10⁹ N∙m² / C².

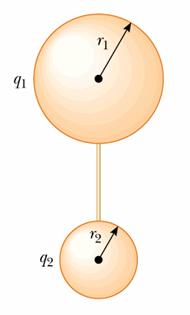
Sa se calculeze:

a)     valoarea sarcinii q₂;

b)    potentialul electric pe suprafata sferei de raza r₁;

c)     intensitatea campului electric intr-un punct M situat in interiorul sferei de raza r₂;

d)    raportul modulelor intensitatilor campurilor electrice pe suprafata sferelor E₁ / E₂

Sa se calculeze diferenta de potential electric intre doua puncte A si B situate la distantele de 1 cm, respectiv 2 cm de un proton. Se dau: masa protonului m_p = 1,67∙10^-27 kg, sarcina electrica elementara e = 1,6∙10^-19 C si constanta lui Coulomb k = 9∙10⁹ N∙m² / C².

O sfera metalica de raza R se incarca la un potential + V. O alta sfera avand raza dubla fata de prima se incarca la un potential - V. Sferele se pun in contact printr-un fir conductor. Sa se exprime potentialul sferei de raza R si sarcina electrica cu care va fi aceasta incarcata.

Un circuit de curent continuu este alimentat de o baterie avand tensiunea electromotoare E = 30 V si rezistenta interna r = 1 Ώ. Circuitul contine o grupare serie compusa din rezistorii R₁ = 5 Ώ, R₂ = 6 Ώ si R₃ = 8 Ώ. Sa se calculeze:

a) rezistenta echivalenta a gruparii serie;

b) intensitatea curentului prin circuit;

c) cu cat se modifica aceasta intensitate daca se scoate rezistorul R₁ din circuit.

Pentru confectionarea rezistentei unui resou electric se foloseste un fir de constantan cu rezistivitatea ρ = 0,5 μ Ώ∙m avand sectiunea S = 0,6 mm² si lungimea l = 60 m. Resoul este alimentat la o tensiune U = 220 V. Sa se calculeze:

a) rezistenta electrica a resoului;

b) intensitatea curentului ce va strabate resoul;

c) de cate ori se modifica intensitatea de la punctul precedent in cazul in care se conecteaza un resou identic in serie, respectiv in paralel cu primul.