| CATEGORII DOCUMENTE |
| Astronomie | Biofizica | Biologie | Botanica | Carti | Chimie | Copii |
| Educatie civica | Fabule ghicitori | Fizica | Gramatica | Joc | Literatura romana | Logica |
| Matematica | Poezii | Psihologie psihiatrie | Sociologie |
CONSIDERATII PRIVIND REZOLVAREA SISTEMELOR DE ECUATII CU COEFICIENTI IN Zn, n N*
Ne propunem sa prezentam câteva aspecte legate de rezolvarea sistemelor de ecuatii cu coeficienti în Zn .Pentru început, facem urmatoarele precizari:
(1) Ecuatia ax=b , a, b K, K corp comutativ, are solutie unica în K.
(2) Într-un corp K avem echivalenta : x=y ax=ay, oricare ar fi a K*.Prin urmare, înmultind ambii membri ai unei ecuatii cu un a K*, obtinem o ecuatie echivalenta cu cea initiala.
(3) Toate metodele de rezolvare a sistemelor învatate în clasa a XI a (regula lui Cramer, Gauss)sunt valabile pentru orice sistem de ecuatii liniare cu coeficienti într-un corp comutativ.
(4) Afirmatiile (1) si (2) ramân valabile si într-un inel comutativ , daca a este inversabil .
(5) Daca a nu este inversabil , ecuatia ax=b în inelul A poate avea zero, una sau mai multe solutii.
(6) Într-un inel comutativ A avem valabila doar implicatia: x=y ax=ay, pentru a A*, a neinversabil De aici rezulta ca, înmultind ambii membri ai unei ecuatii cu coeficienti în A cu a A*, a neinversabil, ecuatia obtinuta nu mai este echivalenta cu prima.
(6) Regula lui Cramer se poate aplica pentru sisteme liniare de n ecuatii cu n necunoscute cu coeficienti în inelul comutativ A atunci când determinantul sistemului este inversabil în A.
Având în vedere ca (Zn , +, *) este corp comutativ daca si numai daca n este numar prim, rezulta urmatoarele reguli practice de rezolvare a sistemelor cu coeficienti în Zn:
1. Daca n este numar prim , atunci se rezolva sistemul cu oricare din metodele cunoscute.
2. Daca n nu este prim , dar determinantul sistemului este element inversabil în Zn, atunci aplicam regula lui Cramer.
3. Daca n nu este prim si determinantul sistemului nu este inversabil în Zn , atunci aplicam metoda reducerii sau substitutiei, încercând , pe cât posibil, sa valorificam (4).Daca acest lucru nu se poate, atunci , la finalul rezolvarii , verificam solutiile obtinute.
Pentru exemplificare prezentam rezolvarile a doua sisteme de ecuatii cu coeficienti în Z6 .
I Sa se rezolve în Z6 sistemul: SolutiaI Calculam
determinantul sistemului :D =
SolutiaI Calculam
determinantul sistemului :D =![]() =
=![]() .Deci, determinantul sistemului este inversabil în Z6
si putem aplica regula lui Cramer.Avem:Dx =
.Deci, determinantul sistemului este inversabil în Z6
si putem aplica regula lui Cramer.Avem:Dx =![]() =
=![]() ;Dy =
;Dy =![]() =
=![]() .Rezulta x =
.Rezulta x =![]() si y =
si y =![]() .Prin urmare , solutia sistemului este S =
.Prin urmare , solutia sistemului este S =![]() .
.
SolutiaII(metoda
substitutiei) Observam ca, în prima ecuatie, coeficientul lui x
este inversabil, inversul lui![]() fiind
fiind![]() . Deci, îl aflam pe
x din prima ecuatie:
. Deci, îl aflam pe
x din prima ecuatie:
![]() .
.![]() .Rezulta:
.Rezulta:![]() .
.
Înlocuind în
a doua ecuatie, obtinem ![]() Deci , solutia
sistemului este S=
Deci , solutia
sistemului este S=![]() .
.
SolutiaIII
(Metoda reducerii) Ne propunem sa reducem
variabila y.Pentru aceasta înmultim ambii membri ai primei
ecuatii cu![]() si ai celei de a doua ecuatii cu
si ai celei de a doua ecuatii cu ![]() .Obtinem (S1):
.Obtinem (S1):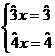
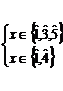 Rezulta
Rezulta![]() .Revenim la prima ecuatie a sistemului.Obtinem
.Revenim la prima ecuatie a sistemului.Obtinem ![]() .Deci, obtinem
perechile
.Deci, obtinem
perechile ![]() si
si ![]() .Dar , la primul pas am înmultit ecuatiile
sistemului cu
.Dar , la primul pas am înmultit ecuatiile
sistemului cu ![]() si , respectiv,
si , respectiv, ![]() care nu sunt
inversabile în Z6.Deci, (S1) nu este echivalent cu
sistemul initial.Vom face, prin
urmare, verificarea
solutiilor.Obtinem solutia sistemului S==
care nu sunt
inversabile în Z6.Deci, (S1) nu este echivalent cu
sistemul initial.Vom face, prin
urmare, verificarea
solutiilor.Obtinem solutia sistemului S==![]() .
.
II. Sa
se rezolve în Z6 sistemul 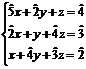 .
.![]()
Solutie Calculam determinantul
sistemului: 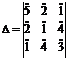 =
=![]() .Evident,
.Evident, ![]() nu este inversabil în Z6, deci, nu putem aplica regula lui Cramer. Observam
ca , în ecuatia a treia, coeficientul
lui x este
nu este inversabil în Z6, deci, nu putem aplica regula lui Cramer. Observam
ca , în ecuatia a treia, coeficientul
lui x este![]() (deci , inversabil).Atunci aflam x din
ecuatia a treia si înlocuim în primele doua.Obtinem:
(deci , inversabil).Atunci aflam x din
ecuatia a treia si înlocuim în primele doua.Obtinem:
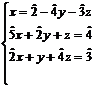
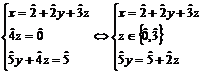 .
. 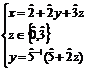
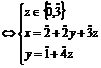
Pentru ![]() , obtinem
, obtinem ![]() , iar pentru
, iar pentru ![]() , obtinem
, obtinem ![]() .Rezulta S=
.Rezulta S=![]()
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 370
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2025 . All rights reserved