| CATEGORII DOCUMENTE |
| Astronomie | Biofizica | Biologie | Botanica | Carti | Chimie | Copii |
| Educatie civica | Fabule ghicitori | Fizica | Gramatica | Joc | Literatura romana | Logica |
| Matematica | Poezii | Psihologie psihiatrie | Sociologie |
Teoria selectiei. Teoria estimatiei
Selectii
Fie un experiment
aleator caruia ii atasam variabila aleatoare (caracteristica) ![]() . Daca
repetam experimentul de n ori in mod independent obtinem un sir de valori de
observatie ale variabilei aleatoare
. Daca
repetam experimentul de n ori in mod independent obtinem un sir de valori de
observatie ale variabilei aleatoare ![]() notate
notate ![]() .
.
Definitie. Multimea valorilor de observatie ale
variabilei aleatoare ![]() avand functia de repartitie F, se numeste selectie de volum n efectuata asupra variabilei aleatoare
avand functia de repartitie F, se numeste selectie de volum n efectuata asupra variabilei aleatoare ![]() (mai precis asupra valorilor variabilei
(mai precis asupra valorilor variabilei ![]() ) cu
functia de repartitie F.
) cu
functia de repartitie F.
Selectia poate fi cu intoarcere sau fara intoarcere; in primul caz elementul extras din populatie este reintrodus la loc inainte de alegerea elementului urmator, iar in al doilea caz elementele alese nu se mai reintroduc in populatia generala.
Daca volumul populatiei generale este suficient de mare, iar volumul selectiei suficient de mic, deosebirea dintre cele doua tipuri de selectie este foarte mica, iar in aplicatii practice o selectie fara intoarcere este considerata ca selectie cu intoarcere.
Vom spune ca o selectie este reprezentativa daca toate valorile de selectie ![]() au aceeasi probabilitate de a intra in
componenta ei.
au aceeasi probabilitate de a intra in
componenta ei.
Functia de repartitie de selectie
Fie o variabila aleatoare ![]() cu functia de repartitie F. Sa presupunem ca
avem o selectie
cu functia de repartitie F. Sa presupunem ca
avem o selectie ![]() , de
volum n efectuata asupra lui
, de
volum n efectuata asupra lui ![]()
Definitie Daca ![]() reprezinta numarul observatiilor in care a
aparut o valoare a caracteristicii
reprezinta numarul observatiilor in care a
aparut o valoare a caracteristicii ![]() mai mica decat x vom numi functie de
repartitie de selectie, functia definita prin relatia
mai mica decat x vom numi functie de
repartitie de selectie, functia definita prin relatia
|
|
Exemplul 7.1. Se efectueaza o selectie
de volum n=100 asupra unei variabile aleatoare ![]() care ne furnizeaza valorile 1, 5, 9, 12 cu
frecventele
care ne furnizeaza valorile 1, 5, 9, 12 cu
frecventele ![]()
Functia de repartitie va fi:

Legatura dintre functia de repartitie teoretica si functia de repartitie de selectie este data de urmatoarea teorema a lui V. I. Glivenko, care ne furnizeaza si justificarea teoretica a utilizarii metodei selectiei.
Teorema 7.1. Daca volumul
selectiei ![]() marimea
marimea
|
|
converge in probabilitate catre zero.
Cu alte cuvinte, pentru ![]() frecventa relativa a evenimentului
frecventa relativa a evenimentului ![]() (adica
(adica ![]() ) converge in
probabilitate catre probabilitatea acestui eveniment (adica F(x)).
) converge in
probabilitate catre probabilitatea acestui eveniment (adica F(x)).
Deci pentru n suficient de mare functia de repartitie de selectie ne da o imagine suficient de precisa despre functia de repartitie teoretica.
Valori tipice de selectie
Momente de selectie. Numim moment de selectie de ordinul r variabila aleatoare:
|
|
In particular, valoarea medie de selectie este:
|
|
Momentul centrat de selectie de ordinul r este:
|
|
Rezulta de aici dispersia de selectie:
|
|
Teorema 7.2. Daca
repartitia teoretica are medie m si dispersia ![]() , atunci
media de selectie are valoarea medie m si dispersia
, atunci
media de selectie are valoarea medie m si dispersia ![]() .
.
Teorema 7.3. Momentele
centrate ale variabilei ![]() tind catre momentele repartitiei normale cand
tind catre momentele repartitiei normale cand ![]() .
.
Teorema 7.4. Valoarea medie
si dispersia momentului de selectie de ordin r, ![]() , sunt
respectiv
, sunt
respectiv ![]() si
si ![]() .
.
Teoria estimatiei
Sa consideram ca avem o selectie dintr-o populatie data a carei functie de repartitiei teoretica are o forma matematica cunoscuta, in care intra anumiti parametri cu valori necunoscute. Exista o infinitate de functii de selectie (statistici) care pot fi propuse ca estimatii pentru parametrii necunoscuti, dar trebuie alese acelea care dau cea mai buna aproximare a parametrilor.
De exemplu, sa presupunem ca studiind un fenomen ajungem la concluzia ca
repartitia lui este normala ![]() deci:
deci:
![]()
Pentru
aplicatii practice trebuie sa determinam valorile numerice ale celor doi
parametri m si ![]() .
.
Repartitia exprimata printr-o functie data in care intra anumiti parametri necunoscuti se spune ca este o lege de repartitie specificata
Daca cunoastem valorile numerice ale parametrilor avem o lege de repartitie complet specificata.
Deci o lege de repartitie nespecificata corespunde unei legi de repartitie necunoscute.
Determinarea
valorilor parametrilor unei repartitii specificate se face cu ajutorul unei
selectii de volum n care conduce la valorile ![]() legate de variabila studiata.
legate de variabila studiata.
In cele ce urmeaza ne vom ocupa de repartitii
specificate care depind de un singur parametru. Deci functia de repartitie
teoretica contine un singur parametru necunoscut ![]() . O selectie de volum n
din colectivitate ne-a dat estimatia
. O selectie de volum n
din colectivitate ne-a dat estimatia ![]() alta selectie de volum n ne da estimatia
alta selectie de volum n ne da estimatia ![]() etc. Repetand
procedeul obtinem estimatiile
etc. Repetand
procedeul obtinem estimatiile ![]() .
.
Deci o estimatie ![]() a lui
a lui ![]() poate fi privita ca o variabila aleatoare cu
valorile posibile
poate fi privita ca o variabila aleatoare cu
valorile posibile ![]()
Estimatii consistente, corecte si absolut corecte, nedeplasate, deplasate
Fie q un parametru al
colectivitatii generale (medie, dispersie, mediana etc.) si ![]() o functie de selectie.
o functie de selectie.
Definitie. Daca ![]() converge in probabilitate catre parametrul
converge in probabilitate catre parametrul ![]() , spunem ca
, spunem ca
![]() este o estimatie
consistenta a lui
este o estimatie
consistenta a lui ![]() .
.
Definitie. Daca:
|
|
spunem ca ![]() este o estimatie
absoluta corecta a parametrului
este o estimatie
absoluta corecta a parametrului ![]() .
.
Teorema 7.5. Momentele de selectie sunt estimatii absolut corecte ale momentelor teoretice.
Teorema 7.6. Dispersia de selectie este o estimatie consistenta pentru dispersia teoretica.
Exemplul
7.4. Fie o schema de tip Bernoulli cu doua stari.
In n observatii independente evenimentul A apare cu probabilitatea p de ![]() ori,
ori, ![]() . Sa se estimeze p si p2
cu ajutorul lui
. Sa se estimeze p si p2
cu ajutorul lui ![]()
R. Verificam daca ![]() este o estimatie a lui p. Avem:
este o estimatie a lui p. Avem:
![]()
![]()
Deci ![]() este o estimatie absolut corecta a lui p.
este o estimatie absolut corecta a lui p.
Avem:
![]()
![]()
deci
![]() , dar
, dar ![]() nu este o estimatie absolut corecta a lui p,
este numai o estimatie corecta.
nu este o estimatie absolut corecta a lui p,
este numai o estimatie corecta.
Functii
de estimatie eficiente.
Metoda verosimilitatii maxime
De multe ori o estimatie nedeplasata nu ne da cea
mai buna aproximare a parametrului de estimat. Valorile posibile ale estimatiei
lui ![]() pot fi mult imprastiate in jurul valorii medii
(daca
pot fi mult imprastiate in jurul valorii medii
(daca ![]() este mare), iar estimatia calculata de o
selectie data poate fi indepartata de valoarea medie a lui
este mare), iar estimatia calculata de o
selectie data poate fi indepartata de valoarea medie a lui ![]() ,
deci se face o eroare alegand
,
deci se face o eroare alegand ![]() ca estimatie pentru
ca estimatie pentru ![]()
Daca ![]() este o estimatie absolut corecta pentru
parametrul
este o estimatie absolut corecta pentru
parametrul ![]() si
si ![]() atunci inegalitatea lui Cebisev:
atunci inegalitatea lui Cebisev:
![]()
da un criteriu pentru alegerea estimatiilor si anume: alegem acea estimatie care are dispersia minima.
Fie ![]() o familie de densitati de probabilitate ale
unei repartitii specificate continue, cu
o familie de densitati de probabilitate ale
unei repartitii specificate continue, cu ![]() parametrul real. Vom admite continuitatea
functiilor
parametrul real. Vom admite continuitatea
functiilor ![]() si existenta derivatelor acestor functii in
raport cu
si existenta derivatelor acestor functii in
raport cu ![]() pana la ordinele necesare calculelor.
pana la ordinele necesare calculelor.
Teorema 7.7.
(Rao-Cramer). Daca ![]() este o estimatie
absolut corecta a parametrului q, atunci:
este o estimatie
absolut corecta a parametrului q, atunci:
|
|
Egalitatea are loc daca si numai daca
exista o constanta k, ce depinde de n si ![]() , asa
incat, aproape sigur:
, asa
incat, aproape sigur:
![]()
Definitie. O estimatie absolut corecta ![]() a parametrului
a parametrului ![]() se numeste estimatie eficienta daca are dispersia
minima.
se numeste estimatie eficienta daca are dispersia
minima.
Daca ![]() este o functie de estimatie absolut corecta,
raportul:
este o functie de estimatie absolut corecta,
raportul:
|
|
se numeste eficienta
lui ![]()
Se observa ca: ![]() . Daca
. Daca ![]() , estimatia
este eficienta.
, estimatia
este eficienta.
Exemplul 7.6. Caracteristica ![]() a elementelor unei populatii are o repartitie
normala
a elementelor unei populatii are o repartitie
normala ![]() cu m cunoscut si
cu m cunoscut si ![]() necunoscut. Consideram ca estimatie a acestui
parametru:
necunoscut. Consideram ca estimatie a acestui
parametru:
![]()
unde variabilele
aleatoare ![]() sunt independente si au aceeasi repartitie ca
sunt independente si au aceeasi repartitie ca ![]() . Sa se determine
eficienta lui
. Sa se determine
eficienta lui ![]()
R. Avem:
![]()
![]()
![]()
Deci ![]() este o estimatie absolut corecta a lui
este o estimatie absolut corecta a lui ![]() . Eficienta sa este:
. Eficienta sa este:

Deci ![]() nu este cel mai eficient estimator.
nu este cel mai eficient estimator.
Teorema 7.9. Doua
estimatii eficiente ale parametrului ![]() sunt egale aproape
sigur.
sunt egale aproape
sigur.
Fie repartitia de tip continu ![]() unde
unde ![]() poate lua orice valoare dintr-un interval I.
Valorile de selectie
poate lua orice valoare dintr-un interval I.
Valorile de selectie ![]() obtinute in urma a n extractii independente
din populatie sunt variabile aleatoare independente cu aceeasi densitate de
probabilitate
obtinute in urma a n extractii independente
din populatie sunt variabile aleatoare independente cu aceeasi densitate de
probabilitate ![]() . Fiecare selectie
. Fiecare selectie ![]() o consideram ca un punct in spatiul de
selectie n-dimensional
o consideram ca un punct in spatiul de
selectie n-dimensional ![]() , iar probabilitatea
elementara a vectorului
, iar probabilitatea
elementara a vectorului ![]() este:
este:
|
|
Definitie. Functia ![]() se numeste functie de verosimilitate.
se numeste functie de verosimilitate.
Definitie. Estimatia ![]() se numeste estimatie de verosimilitate daca
se numeste estimatie de verosimilitate daca ![]() este un punct de
maxim pentru functia de verosimilitate.
este un punct de
maxim pentru functia de verosimilitate.
Rezulta ca ![]() este o solutie a
ecuatiei:
este o solutie a
ecuatiei:
|
|
Ecuatia (7.11.) se numeste ecuatie de verosimilitate.
Teorema 7.10. Orice
estimatie eficienta a parametrului ![]() este o estimatie
de verosimilitate maxima.
este o estimatie
de verosimilitate maxima.
Exemplul 7.8. Fie repartitia normala cu densitatea de probabilitate: ![]() . Sa se estimeze media m.
. Sa se estimeze media m.
R. Avem:
![]()
Din teorema 7.7. rezulta ca:
![]()
este o functie de estimatie eficienta a lui m deoarece:
![]()
si
![]()
![]() .
.
Rezulta ca ![]() este o estimatie absolut corecta. Functia de
verosimilitate este:
este o estimatie absolut corecta. Functia de
verosimilitate este:
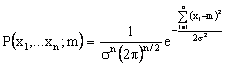
iar din ecuatia verosimilitatii maxime ln P=0 rezulta ![]() sau
sau ![]() .
.
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 3907
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2025 . All rights reserved