Valoarea in timp a banilor

Valoarea in timp a banilor

Multe decizii financiare se refera la situatii in care o persoana fizica sau juridica efectueaza anumite plati la un moment in timp, si primeste fonduri la un alt moment. Banii care se platesc sau se incaseaza la momente diferite in timp au valori diferite, iar aceasta diferenta de valoare este recunoscuta si denumita analiza valorii in timp a banilor.

Aceasta analiza se realizeaza utilizand concepte si procedee care se bazeaza pe tehnica dobanzii compuse. Dobanda reprezinta o cheltuiala importanta pentru debitor si un venit pentru creditor. Deoarece dobanda reprezinta un cost legat de timp, iar timpul inseamna bani, timpul constituie o variabila importanta luata in considerare in orice decizie economica, si indeosebi, in deciziile privind fluxurile financiare si monetare.

In acest sens, utilizand conceptul de dobanda compusa se poate determina valoarea viitoare a imobilizarilor financiare,   prin procedeul compunerii valorilor, in functie de dobanda compusa. Totodata, luand in considerare mecanismul dobanzii compuse si costul legat de trecerea timpului, se poate determina valoarea prezenta, care reprezinta suma ce trebuie investita in prezent la o anumita rata a dobanzii pentru a obtine o anumita valoare viitoare, determinare realizata prin procedeul actualizarii valorilor.

Procedeul de compunere este procedeul de determinare a valorii viitoare (VV) a unui flux de numerar sau a unei serii de fluxuri de numerar. Valoarea viitoare, sau suma compusa, este egala cu valoarea de inceput, plus dobanda acumulata.

Valoarea viitoare (pentru o singura data) se determina prin formula:

(43)

unde:

V V = valoarea viitoare;

V P = valoarea prezenta;

k = rata dobanzii;

n = numarul de perioade (ani).

Exemplu:

Suma de 1.000.000 dolari compusa pe o perioada de 3 ani la rata dobanzii de 4 % anual:

Procedeul de actualizare este procedeul de determinare a valorii prezente VP a unui flux de numerar sau a unei serii de fluxuri de numerar, procedeul de actualizare fiind inversul celui de compunere.

Valoarea prezinta (pentru o singura suma):

(44)

Exemplu:

Suma de 1.000.000 dolari actualizata pe o perioada de doi ani la o rata a dobanzii de 4 %

O anuitate se poate defini ca o serie de plati periodice egale (A) efectuate pe un numar specificat de perioade.

Valoarea viitoare a unei anuitati

(45)

Exemplu:

Valoarea viitoare a unei anuitati VVA cu 3 plati a cate 1.000.000 lei, la o rata de 4 %:

Valoarea prezenta a unei anuitati:

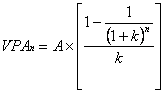(46)

Exemplu

Valoarea prezenta a unei anuitati VPA cu 3 plati a cate 1000.000 la o rata de 4 %:

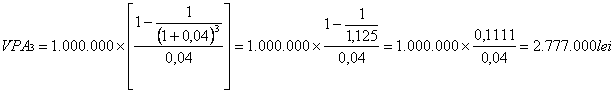
O anuitate la care platile se efectueaza la sfarsitul fiecarei perioade se numeste o anuitate obisnuita. Formulele prezentate mai sus valabile pentru acest gen de anuitati.

Daca fiecare plata are loc la inceputul perioadei si nu la sfarsitul sau, atunci avem de a face cu o anuitate speciala. Valoarea prezenta, VP, a fiecarei plati va fi mai mare, pentru ca perioada de actualizare va fi mai mica cu un an (o perioada) si astfel valoarea prezenta VP a anuitatii, va fi de asemenea, mai mare. In mod similar, valoarea viitoare a unei anuitati speciale, VV, va fi de asemenea mai mare, pentru ca fiecare plata va suferi procesul de compunere pentru inca un an (o perioada).

Urmatoarele formule pot fi folosite pentru a modifica VPo si VVo, pentru o anuitate obisnuita in VPs si VVs, pentru o anuitate speciala.

(47)

(48)

Daca fluxurile de numerar sunt inegale, nu se pot folosi formulele aplicate anuitatilor. Pentru a determina valoarea prezenta, VP, sau valoarea viitoare, VV, a unei serii de fluxuri de numerar inegale, trebuie sa se gaseasca VP sau VV ale fiecarui flux de numerar, si apoi se insumeaza toate aceste valori. Totusi, daca unele dintre fluxurile de numerar pot fi combinate ca sa constituie o anuitate, se pot folosi formulele valabile pentru anuitate, pentru a se calcula valoarea prezenta VP sau valoarea viitoare VV a acelei parti din seria de fluxuri de numerar.

Calcularea valorii in timp a banilor se face, in general, folosind ecuatii care au patru variabile, astfel incat daca trei dintre ele sunt valori cunoscute, ecuatia poate fi rezolvata pentru a determina cea de a patra variabila, care constituie necunoscuta.

Daca se cunosc fluxurile de numerar dintr-o serie si valoarea prezenta, VP, sau valoarea viitoare, VV, se poate afla rata dobanzii sau rata de actualizare (rata costului de oportunitate). De exemplu, un imprumut bancar trebuie rambursat prin 3 plati a cate 100.000 lei, imprumutul avand o valoare prezenta de VP = 2.775.000 lei, atunci se poate determina rata dobanzii care face ca suma valorilor prezente,VP, ale platilor succesive sa fie de 2.775.000 lei. Deoarece aceasta este o anuitate, se poate proceda dupa cum urmeaza:

Se scrie ecuatia corespunzatoare,

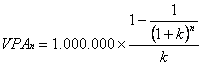(49)

Pentru a gasi valoarea ratei dobanzii, k , se cauta in tabelele speciale pentru VVA si VPA, pe randul al treilea, corespunzator unui numar de 3 perioade, si se gaseste valoarea care corespunde coloanei 4, adica unei rate a dobanzii de 4 %. Evident, utilizand tehnica de calcul, prin modele algoritmice adecvate, valoarea lui k se determina rapid. Daca factorul nu apare in tabel, aceasta inseamna ca rata dobanzii nu este numar intreg, in acest caz nu se poate utiliza aceasta procedura, in practica apelandu-se la un calculator financiar. Evident, utilizand tehnica de calcul, prin modele algoritmice adecvate, valoarea lui k se determina rapid.

Multe contracte stipuleaza plati mai frecvent, unele banci operand cu dobanda compusa zilnic. Cand procedeul de compunere are loc mai frecvent decat o data pe an, acest fapt trebuie luate in considerare, determinandu-se rata anuala efectiva a dobanzii (RAE).

(50)

Pentru o compunere semestriala, rata anuala efectiva a dobanzii este de 4,04%,

Aceasta rata a dobanzii poate fi apoi utilizata pentru determinarea valorii prezente VP sau valorii viitoare VV a fiecarei plati (acum trebuie sa se utilizeze un calculator financiar, deoarece tabelele nu pot fi utilizate)

Daca platile anuale in valoare de cate 1.000.000 lei fiecare ar fi fost de fapt plati de cate 500.000 lei, fiecare platibile la cate 6 luni (deci semestrial), pentru determinarea valorii prezente VP sau valorii viitoare VV a acestei noi serii, va trebui sa se utilizeze rata periodica a dobanzii in valoare de 4 % : 2 = 2 %

Ecuatia generala pentru determinarea valorii viitoare, pentru orice numar de perioade de compunere pe an, este urmatoarea:

(51)

unde:

k_nom. = rata nominala, sau cotata a dobanzii;

m = numarul de perioade de compunere pe un an;

n = numarul de ani.

Un imprumut amortizat este un imprumut care se ramburseaza in rate egale, pe o anumita perioada de timp. O schema de amortizare a imprumutului arata, prin defalcare, care este portiunea din suma de plata care reprezinta dobanda, care este cea care constituie rambursarea transei din suma initiala imprumutata, si ce a ramas de rambursat la fiecare moment in timp.

Calculatoarele financiare dispun de programe care pot sa realizeze toate operatiile necesare.