Corelatia sau asocierea variabilelor

Corelatia sau asocierea variabilelor

Legatura dintre 2 sau mai multe variabile se poate studia folosind 2 tehnici :

a) corelatia - care arata cat de puternica este legatura ;

b) regresia - care explica o variabila pe baza evolutiei altei variabile considerata a fi cauza.

Prin corelatie se poate afla tendinta generala a masurii in care 2 variabile variaza la unison (se manifesta la fel).

Corelatia poate fi de 2 feluri :

a) corelatia parametrica - este utilizata in cazul variabilelor cantitative si se bazeaza pe parametrii distributiei (media si dispersia) ;

b) corelatia neparametrica (sau asociere) - utilizata atunci cand cel putin una din variabile nu este numerica.

Coeficientii de corelatie iau valori cuprinse intre-1 si +1

Cu cat un coeficient de corelatie este mai apropiat de zero cu atat legatura sau asocierea este mai slaba.

Cu cat un coeficient de corelatie este mai apropiat de +1 cu atat legatura este mai intensa si directa.

Cu cat un coeficient de corelatie este mai apropiat de -1 cu atat legatura este mai intensa dar invers.

Corelatia parametrica pentru seriile simple

*** pentru rezolvarea unei probleme se poate alege una din variantele de calcul de mai jos :

Varianta 1:

D_x - abatere medie patratica a lui x

- calcul x mediu : = 45 / 6 = 7.5

- calcul y mediu : = 48 / 6 = 8

Varianta 2:

Prin transformari elementare formula initiala devine o formula de calcul prescurtat :

Semnificatia coeficientului de corelatie parametric

Se verifica ipoteza nula, adica aceea care presupune ca perechiile de variabile x si y sunt intamplatoare, legatura dintre ele fiind nula. In caz contrar daca valoarea calculata a testului este superioara celei tabelare (la nivelul de incredere stabilit) atunci coeficientul de corelatie este seminficativ diferit de zero, existand o relatie seminificativa intre cele 2 variabile.

Pentru verificarea semnificatiei se pot utiliza 2 procedee :

a) testul "t"

Aceasta valoare se compara cu valoarea tabelara (pg. 298 din carte) pentru n-2 grade de libertate.

?????

P=0.95

(1-P)0.05 4.12 > t₄; 0.95; 2.776 (valoarea 2.776 - din carte pg. 298)

b) coeficientul critic de corelatie C_c

Este cel mai mic coeficient de corelatie semnificativ. Sub nivelul lui coeficientul calculat nu are semnificatie.

Coeficientul critic se calculeaza in functie de numarul subiectilor. (n-2 grade de libertate) si de probabilitatea considerata.

6 subiecti → 4 grade de libertate

Aplicatie

Sa se calculeze coeficientul critic pentru 42 de subiecti.

- se stabilesc gradele de libertate = 40 → 2.021 (din tabela de la pg 298)

Aplicatie

- calcul x mediu : = 49 / 7 = 7

- calcul y mediu :

Varianta 1:

- abateri medii :

Varianta 2:

testul "t"

→ se compara cu valoarea tabelara (pg. 298 carte) pentru 5 grade de libertate → 2.57

coeficientul critic de corelatie :

→ 0.64 = valoarea nu are seminificatie (numarul de subiecti este mic)

Corelatia neparametrica sau asocierea variabilelor categoriabile

Conditia pentru independenta variabilelor, adica pentru lipsa asocierii, este ca frecventele empirice (cele initiale) cuprinse in tabel sa fie asemanatoare cu frecventele teoretice (cele calculate).

Aceste frecvente teoretice se obtin prin inmultirea totalului liniei cu totalul coloanei respective si raportarea acestui produs la totalul subiectilor.

unde : l_i = linia i ; c_j = coloana j

Diferenta dintre distributia empirica si cea teoretica se calculeaza pe baza testului hi patrat.

unde : f_em = frecventa empirica

Aplicatie

calcul valori teoretice (cele din paranteze) :

calcul pentru: t A; m A; i A

calcul pentru : t B; m B; i B

calcul pentru : t C ; m C ; i C

→ daca NU seamana → exista legatura

→ daca NU seamana mult → exista legatura mare

2) calcul hi patrat:

A B C

In sine marimea lui hi patrat nu masoara intensitatea (marimea) asocierii ci doar existenta sau seminificatia asocierii.

Valorile calculate a ale lui hi patrat se compara cu valoarea sa tabelara pentru (r-1)(c-1) (3-1)(3-1) si rezulta 4 grade de libertate si probabilitatea considerata de 95% (p=95%).

Se poate garanta cu o probabilitate de peste 99.9 % ca distributiile nu sunt independente si sunt asociate semnificativ.

Pentru a calcula intensitatea legaturii se utilizeaza coeficientul de asociere :

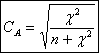
Seriile cronologice (dinamica, de timp)

Este un sir de valori care reflecta evolutia unei variabile la anumite momente sau perioade succesive de timp.

Indicatorii unei serii cronologice se pot obtine folosind :

a) o baza fixa - adica un nivel de referinta neschimbat pentru intreaga perioada analizata.

Y_t y₁

b) o baza in lant sau mobila - adica baza de comparare - este nivelul din perioada imediat anterioara.

Y_t < y_t-1 (yt se compara cu _yt-1)

Sistemul de indicatori ai seriilor cronologice

1) Indicatori absoluti - arata nivelul fenomenului sau modificarile de nivel survenite in timp :

a) nivelul (y_t) care constituie baza de calcul

b) sporul (s_i) sau modificarea absoluta - arata cu cat s-a modificat fenomenul din perioada analizata fata de o perioada de referinta fixa sau mobila.

Sporul se calculeaza ca diferenta intre 2 niveluri.

S_bf = y_t - y₁ spor cu baza fixa

S

S_bl = y_t - _yt-1 spor cu baza in lant

Nota: suma sporurilor cu baza in lant este egala cu sporul in baza fixa a perioadei analizate.

2) Indicatori relativi - arata proportia nivelului sau a declajului inregistrat intr-o perioada fata de nivelul considerat ca baza de raportare.

a) indicele dinamicii (j_t) - arata de cate ori s-a modificat nivelul in comparatie cu baza de raportare.

Indicele se poate exprima fie in coeficienti fie in procente.

J_bf = y_t / y₁

J_t

J_bl = y_t / _yt-1

Nota : produsul indicilor cu baza in lant este egal cu indicii in baza fixa a perioadei analizata.

b) ritmul dinamicii - arata cu cat s-a modificat procentual fenomenul.

R = j - 1

3) indicatori medii - redau fie nivelul mediu fie cresterea sau descresterea medie - adica modificarea medie in timp a fenomenului.

a) nivelul mediu - se calculeaza ca o medie aritmetica a nivelurilor anuale

b) sporul mediu - este media aritmetica a sporului cu baza in lant

c) indicele mediu - arata de cate ori s-a modificat in medie fenomenul in perioada analizata.

explicatie: a crescut in medie cu 90 .

explicatie: de la un an la altul a crescut cu 1.257

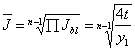
In principiu relatia se logartimeaza.

Nota : cand nr. termenilor seriei 5, 9, 17, etc, cand radicalul este de 4, 8, 16, indicele se poate calcula direct prin apasarea tastei radical a calculatorului de 2, 3, sau 4 ori.

d) ritmul mediu - este egal cu

RM