STRUCTURI STATISTICE

Notiunea de structura statistica (model statistic) are acelasi rol in teoria deciziilor statistice si statistica matematica, ca si spatiul de probabilitate in teoria probabilitatilor.

In problemele de decizie statistica, analiza riguroasa in care se realizeaza experimentarea, este pusa in evidenta de structura statistica a observatiilor introdusa de Fraser [47].

Utilizarea structurilor statistice in descrierea problemelor de decizie a fost data de J. R. Barra [2]. Studiul structurilor statistice, caracteristicilor de suficienta, libertate conditionata a s-algebrelor si statisticilor a fost dezvoltat de J. L. Sole in [94], [95].

In lucrare se introduce notiunea de structura statistica a deciziilor, fapt ce permite o tratare unitara si mai generala a problemelor de decizii statistice.

Structuri statistice dominate

Fie P o familie de probabilitati (repartitii) definite pe spatiul (W K), se numeste structura statistica tripletul (W K P

Spatiul W reprezinta spatiul observatiilor si se presupune deci ca aceste observatii corespund elementului aleator X despre a carui lege de probabilitate (repartitie) necunoscuta se admite apriori ca apartine familiei cunoscute. In continuare se presupune ca familia P este descrisa cu ajutorul unui indice numit parametru (stare) si se va scrie atunci: P

Exemplul 1.1. Fie W multimea intregilor nenegativi, K familia tuturor partilor si P familia legilor Poisson de parametru l, atunci tripletul (W K P ) constituie o atructura statistica.

Exemplul 1.2. (R, B_R unde N(m,1) este legea normala, constituie o atructura statistica.

Definitia 1.1.2. Structura statistica (W K P ) se numeste dominata daca exista o masura pozitiv s-finita, m W K R⁺ astfel ca orice lege PIP sa admita o densitate de probabilitate in raport cu m

Teorema data mai jos poate fi considerata ca o definitie echivalenta a structurilor statistice dominate.

Teorema 1.1.3. Structura statistica este dominata daca exista o masura pozitiva s-finita astfel ca orice PIP sa fie absolut continua in raport cu m

Demonstratia rezulta imediat din teorema lui Radon-Nicodym [36] si teorema 2, 2, pag. 248 [2].

Teorema urmatoare arata ca, pentru structuri dominante este intotdeauna posibil sa alegem in calitate de masura care domina o probabilitate.

Definitia 1.1.4 Fie doua structuri statistice (W K P ) si (W K P ) cu spatiul observatiilor comun.

i) Se spune ca structura statistica (W K P ) domina structura (W K P ') si notam

P >> P '. Daca P(A)=0 PI P T P'(A)=0 P I P

ii) cele doua structurile sunt echivalente daca P >> P 'si P >> P.

Propozitia 1.1.4. Structura statistica (W K P este dominata daca si numai daca exista o subfamilie P P cel mult numarabila astfel ca P >> P

Demonstratie: Pentru a demonstra suficienta, notam cu P^*=.Se verifica usor ca P^* este o probabilitate si P^*(A)=0 implica, i=1, 2,. si deoarece P >>P atunci P(A)=0 PIP deci P^*>>P, PIP si din teorema 1.1.3. rezulta ca structura statica (W K P este dominanta.

Pentru a demonstra necesitatea, presupunem ca exista o masura pozitiva s-finita astfel ca m >> P_q qIQ . Masura pote fi considerata chiar marginita. Deoarece m este s-finita, exista si W m(A_i)< i

Fie probabilitatea P⁰ definita pe spatiul (W K) prin care formula P⁰(A)=care este echivalenta cu m si deci P⁰>>P_q qIQ

Fie p_q=dP_q/dm , A_q si F clasa reuniunilor numarabile de multimi A_q qIQ. Se vede ca M=exista, deoarece este suficient sa consideram multimea B= unde A_i= F si M-1/i<m(A_i) M. Insa deoarece elementele familiei F sunt reuniuni cel mult numarabile de multimi A_q qIQ rezulta ca exista q_iIQ astfel ca B= pentru orice qIQ

A_q=(A₀B) Tm(A₀ B) M=m(B) adica m(A₀B)=0 si deoarece m<<P_q qIQ rezulta P_q(A₀B)=0 pentru orice qIQ. Dar atunci pentru orice AIF trebuie sa fie indeplinita egalitatea P_q(AB)=0.

Fie AI F astfel ca unde q_i sunt definiti de B. Deoarece >0 iar integrala 1 i este egala cu zero, atunci m(A )=0 i ce inseamna ca m(A B)=m(A) si din absolut continuitate rezulta ca P_q(A B)=0 pentru orice qIQ

Teorema 1.1.5. Structura statistica este dominanta daca si numai daca exista o lege de probabilitate P^* pe (W K ) numita privilegiata, care domina (W K P ) si care satisface conditiile:

a)      P^x este o combinatie strict convexa de elementele unei subfamilii cel mult

numarabile P P

P^*=

b) P^* este echivalenta cu P adica AI K , [P(A)=0, PIP ] P^*(A)=0.

c) Orice masura care domina structura statistica (W K P ) domina si probabilitatea

privilegiata P^*.

Demonstratia rezulta imediat din propozitia 1.1.4.

1.2. Produs de structuri statistice

Produsele de structuri statistice introduse descriu procesele de decizie secventiale.

Definitia 1.2.1. Fie structurile statice (W K P ) si (W K P

Se numeste produs al celor doua structuri si se noteaza (W K P A W K P ) structura (W K P ) unde W W AW K K AK P P A P si

P A P

Definitia 1.2.2. Fie structura (W K P_o) si (W K P_o ) doua structuri statistice cu acelasi spatiu al parametrilor. Se numeste produs restrans al structurilor si se noteaza

W K P _o W K P_o ) structura (W W K AK

In acest caz particular, produsul restrans de un numar finit de ori a unei structuri, se numeste selectie empirica.

Produsul de structuri corespunde unui sistem de observatii indepartate.

In definitia 1.2.2. se presupune ca cele doua structuri au acelasi spatiu de parametri, in timp ce in definitia 1.2.1. aceasta nu se face.

Se da in continuare o teorema data de Leonte Ar. in [59].

Teorema 1.2.3 Daca structurile statistice (W_i K_i P _i sunt dominate, atunci produsul lor restrans este o structura dominanta.

Demonstratie: Din teorema 1.1.3. rezulta ca exista doua masuri de probabilitate privilegiate P^*₁, P^*₂ echivalente cu P si P . Daca A este masurabila in spatiul produs (W W K AK ) atunci P₁ P₂(A)= = . Fie P P^*₂ (A)=0, rezulta ca P^*₂ (A_w1)=0, P^*₁. a.s. deci P₁. a.s. pentru orice P₁IP .

Astfel (P₁ P₂)(A)=0

Asemanator, deducem in continuare ca (P₁ P₂)(A)=0 pentru orice P₂IP Prin urmare, P P=0 este o probabilitate echivalenta cu P₁ P₂.

Observatie:

Fie: P= P₁ P₂

In conditiile teoremei 1.2.3. (dP/dP^*)(w₁,w₂)= (dP₁/dP^*₁)(w₁) (dP₂/dP^*₁)(w₂) care se extinde fara dificultate pentru produse cu numar finit de factori.

Deci, in cazul cand structurile sunt dominate functiile de densitate p_q(w)=(dP_q/dP^*)(w), se numesc functii de verosimilitate, care pentru structuri de produse devin L (w,w q q )=p(w)p (w ) si pentru produsul restrans L(w,w q)= p(w)p (w

In continuare in lucrare se va presupune ca n-ori si este spatiu metric euclidian, iar K este -algebra- multimilor boreliene.

1.3. Separabilitatea spatiului starilor dintr-o structura statistica

In acest paragraf se dau demonstratii mai generale a separabilitatii spatiului parametrilor (starilor) utilizand teoremele de comvergenta slaba a masurilor de probabilitati [8] ceea ce in [111] se considera prin ipoteza.

Fie structura statistica (W K P in care se considera ca exista o corespondenta bijectiva intre multimea probabilitatilor definite pe (W K ) si spatiul starilor Q. O multime AIK a carei frontiera, notata A satisface conditia P( A)=0 se numeste P-continua.

Definitia 1.3.1. Fie structura statistica (W K P sirul converge slab catre si notam I daca pentru orice f, functie reala, continua si marginita pe W avem cand i

Definitia 1.3.2. Fie structura statistica (W K P ) si IQ un sir de stari. Sirul q_i converge regulat catre starea q notat daca q_iq daca Teorema urmatoare da conditii echivalente pentru convergenta regulata a unui sir de stari, dedusa din convergenta slaba a masurilor de probabilitate.

Teorema 1.3.3. Fie structura statistica (W K P

Atunci urmatoarele cinci afirmatii sunt echivalente.

a) q_iq cand i

b) lim=oricare ar fi f, functie reala uniform continua si marginita;

c) sup 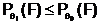oricare ar fi multimea F inchisa;

d) inf P(G) oricare ar fi multimea G deschisa;

e) lim=oricare ar fi AIK cu =0

Demonstratia acestei teoreme rezulta din definitia 1.3.2. si teorema 2.1. pag.

In practica este mai usor sa demonstram convergenta regulata aratand ca pentru o clasa speciala de multimi A

Teorema 1.3.4. Fie structura statistica (W K P    cu proprietatile:

A - este inchisa in raport cu intersectiile finite;

- si orice multime deschisa AIK este o reuniune finita sau numarabila de elemente din A Daca pentru orice AIA atunci q_i q

Demonstratie: Daca A₁, .,A_mIA atunci de asemenea IA . Atunci formula +. trecand la limita si tinand cont de ipoteze rezulta ca: cand i

Daca G este deschisa, atunci G=A_kIA , k =1,2,. Fiind dat e> alegem m astfel ca P(G)-e si deoarece e<

Din conditia (d) a teoremei 1.3.3 rezulta in final teorema.

Definitia 1.3.5. Structura statistica se numeste discreta daca exista o multime A cel mult numarabila astfel ca P(A)=1 oricare ar fi qIQ

Aceasta definitie este echivalenta cu faptul ca, fiecare masura de probabilitate din familia P este densa. Abraham Wald in [111] da doua definitii diferite ale convergentei regulate una pentru structuri cu element aleator cu functii de repartitii continue si una pentru structuri discrete.

Observatia si teorema urmatoare arata ca definitia introdusa este adevarata pentru structuri discrete sau dominante.

Observatia 1.3.6. Daca structura statistica (W K P este discreta atunci q_i q daca , q,wIA

Teorema 1.3.7 Fie structura statistica (W K P dominata, unde p_q(w)=dP_q/dP^*, P^* fiind probabilitatea privilegiata care domina structura.

Sirul de stari q_i converge regulat catre starea q IQ daca oricare ar fi wIWN(P ) unde N(P ) este o multime P -neglijabila.

Demonstratie. Din teorema lui Scheffe [8] rezulta ca =care implica si din definitia 1.3.3. rezulta teorema.

Teorema lui Kolgomorov de existenta a masurilor ne permite sa extindem familia P la masuri de probabilitate pe spatii produs, W=R daca este indeplinita conditia P_n-1=P_n j _n n>1unde j_n este proiectia din spatiu Rⁿ in R^n-1.

Teorema 1.3.8. Fie structura statistica (W K P

Sirul q_i converge regulat, catre stare q daca si numai daca converge in raport cu topologia generata de una din bazele:

a)

b)

c)

Demonstratia rezulta din teorema 3 pag.

Teorema 1.3.9. Fie structura statistica (W K P ) si Q spatiul starilor corespunzatoare masurilor de probabilitate cu suport finit. Atunci Q este dens in Q in raport cu convergenta regulata.

Demonstratie. Consideram sistemul de vecinatati V (q₀) de forma (a). pentru orice multime nevida B din partitia finita generata de F₁, F₂,.,F_k alegem un singur punct si concentram in aceasta (B).

Masura rezultata are suport finit si care apartine lui V ) deoarece ea coincide cu pe orice multime F_i si din teorema 1.3.8. (a) rezulta teorema.

Fiind data structura statistica a observatiilor (W K P ) discreta pe spatiul starilor se defineste urmatoarea semidistanta. Fie d(q q )=

Aceasta permite definirea convergentei punctuale urmatoare.

Definitia 1.3.10 Sirul de stari (q_i) converge punctual catre starea q daca d(q_i q pentru i

Teorema 1.3.11. Fiind data structura statistica a observatiilor discrete atunci spatiul metric al starilor (Q,d) este separabil.

Demonstratie. Fara a pierde din generalitate consideram spatiul starilor Q Q corespunzator unui element aleator care nu ia decat valori intregi. Evident separabilitatea lui Q este demonstarta daca aratam separabilitatea lui Q . Fie Q si r rational astfel ca P_q(x_j=i_j, j= =r, si P_q(x_j>k_j, j=)=o Evident Q este o submultime numarabila si se verifica usor ca este densa in Q

Corolar 1.3.13. Din teorema 1.3.7. si observatia 1.3.6. rezulta ca, convergenta punctului implica convergenta regulata.