| CATEGORII DOCUMENTE |
Formule utile in rezolvarea problemelor
In tabelul nr.1 sunt prezentate formulele de calcul pentru media, dispersia si abaterea medie patratica corespunzatoare colectivitatii generale si colectivitatii de selectie.
|
Notiuni |
Indicator |
Relatii de calcul |
|||
|
Caracteristica nealternativa |
Caracteristica alternativa |
||||
|
0 |
1 |
2 |
3 |
||
|
Colectivitate generala |
Media |
|
|
||
|
Dispersia |
|
|
|||
|
Abaterea medie patratica |
|
|
|||
|
Colectivitatea de selectie |
Media |
|
|
||
|
Dispersia |
|
|
|||
|
Abaterea medie Patratica |
|
|
|||
Numim eroare de reprezentativitate numarul notat si definit astfel:
![]()
Conditia ca media unui esantion sa fie reprezentativa:
![]() .
.
Daca numarul esantioanelor posibile este k, iar frecventele mediilor de selectie posibile este ns atunci eroarea medie de reprezentativitate este :
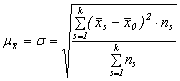 .
.
Eroarea limita maxima admisa (![]() ) :
) :
![]() ,
,
unde ![]() se obtine
din
se obtine
din ![]()
![]()
![]() fiind functia Gauss-Laplace ale carei valori sunt
tabelate.
fiind functia Gauss-Laplace ale carei valori sunt
tabelate.
SELECTIA ALEATOARE SIMPLA
Eroarea medie de reprezentativitate pentru caracteristica nealternativa:
pentru selectia repetata:
![]()
-pentru selectia nerepetata:
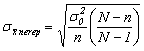
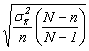
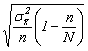
Eroarea medie de reprezentativitate pentru caracteristica alternativa:
pentru selectia repetata:
![]()
-pentru selectia nerepetata:
![]() .
.
Eroarea limita maxima admisa:
-pentru selectia repetata:
![]() respectiv
respectiv ![]()
-pentru selectia nerepetata:
![]() , respectiv
, respectiv 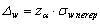 .
.
Intervalul de incredere al mediei colectivitatii generale:
-pentru caracteristica nealternativa:
![]()
-pentru caracteristica alternativa:
w Dw < p < w Dw .
Intervalul de variatie al nivelului totalizat al caracteristicii :
-pentru caracteristica nealternativa:
![]()
-pentru caracteristica alternativa:
![]()
Volumul esantionului:
-pentru sondajul simplu repetat:
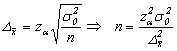
-pentru sondajul simplu nerepetat:
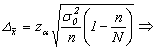
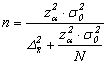 .
.
Volumul esantionului in cazul
modificarii erorii limita maxime admise (![]() ) :
) :
-pentru selectia repetata:
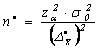
-pentru selectia nerepetata:
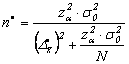 .
.
SELECTIA TIPICA (STRATIFICATA)
Modalitati utilizate pentru repartizarea esantionului pe subesantioane corespunzator tipurilor calitative:
a) In selectia tipica neproportionala repartizarea in mod egal a
esantionului pe subesantioane indiferent de numarul unitatilor ce compun
straturile populatiei totale: ![]() unde k este numarul de straturi in populatia
totala iar ni este dimensiunea fiecarui subesantion.
unde k este numarul de straturi in populatia
totala iar ni este dimensiunea fiecarui subesantion.
b)Selectia tipica proportionala care consta in repartizarea
esantionului pe subesantioane in functie de ponderea fiecarui strat in colectivitatea generala:
![]() de unde
de unde ![]()
c) Pentru selectia tipica optima la formarea subesantioanelor se ia in consideratie atat ponderea fiecarui strat in colectivitatea generala cat si gradul de omogenitate al straturilor, reprezentat de abaterea medie patratica:
![]() .
.
Formulele utilizate in cazul sondajului tipic proportional:
-eroarea medie de reprezentativitate:
![]() pentru selectia
repetata
pentru selectia
repetata
![]() pentru selectia
nerepetata,
pentru selectia
nerepetata,
unde ![]() este media
dispersiilor straturilor (grupelor);
este media
dispersiilor straturilor (grupelor);
-eroarea limita maxima admisa:
![]() pentru selectia
repetata
pentru selectia
repetata
![]() pentru selectia
nerepetata,
pentru selectia
nerepetata,
-estimarea mediei la nivelul colectivitatii generale:
![]() <
<![]() <
<![]()
unde ![]() este media mediilor
de grupa;
este media mediilor
de grupa;
-estimarea nivelului totalizat al caracteristicii:
![]() <
<![]() <
<![]()
-redimensionarea esantionului:
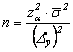 pentru selectia repetata
pentru selectia repetata
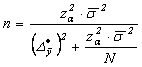 pentru selectia
nerepetata.
pentru selectia
nerepetata.
SELECTIA DE SERII
Esantionul este format dintr-un numar de serii notat cu r, iar in colectivitatea generala numarul seriilor se va nota cu R .
Eroarea medie de reprezentativitate:
-pentru caracteristici nealternative:
![]() ,
,
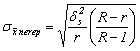 ;
;
unde : 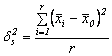 este dispersia dintre
serii.
este dispersia dintre
serii.
-pentru caracteristici alternative:
![]() ,
,
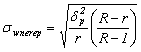 ;
;
-eroarea limita maxima admisa:
![]() pentru selectia
repetata
pentru selectia
repetata
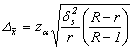 pentru selectia
nerepetata.
pentru selectia
nerepetata.
-redimensionarea esantionului:
![]() pentru selectia
repetata
pentru selectia
repetata
![]() pentru selectia
nerepetata.
pentru selectia
nerepetata.
TESTE DE SEMNIFICATIE
Folosim "ipoteza diferentei nule" care presupune ca nu exista diferente semnificative intre parametrii de sondaj si parametrii populatiei sau intre parametrii de sondaj a doua esantioane aleatoare.
Compararea mediei de sondaj cu media populatiei intr-o repartitie normala:
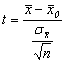 ,
,
daca t > se respinge ipoteza diferentei nule, unde![]() pentru un nivel de semnificatie de 5%.
pentru un nivel de semnificatie de 5%.
Compararea mediilor a doua esantioane mari:
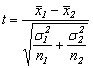
Pentru un nivel de semnificatie 5% daca ½t½< se accepta ipoteza si se considera diferentele nesemnificative.
Se respinge ipoteza daca ½t½> , avand un nivel de semnificatie de 1%.
Compararea a doua proportii de sondaj pentru o caracteristica alternativa:
nu cunoastem proportia p in cele doua populatii din care s-au facut esantioanele. Admitem
ca ![]() .
.
Admitem ca ![]() si daca
si daca  > atunci diferenta dintre cele doua
proportii este semnificativa.
> atunci diferenta dintre cele doua
proportii este semnificativa.
proportiile in cele doua populatii din care s-au format esantioanele nu sunt egale, de aceea folosim dispersiile esantioanelor.
Daca 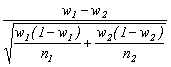 > , atunci diferenta dintre cele
doua proportii este semnificativa.
> , atunci diferenta dintre cele
doua proportii este semnificativa.
comparam proportiile esantioanelor
cu ![]()
Calculam 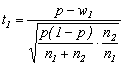 si daca
si daca ![]() diferenta este
semnificativa.
diferenta este
semnificativa.
Compararea mediei de sondaj (pentru un esantion de volum redus) cu media populatiei intr-o repartitie Student:
![]()
![]() se citeste din tabelul cu valorile
repartitiei Student pentru un nivel de semnificatie si (n-1) grade de libertate.
Daca
se citeste din tabelul cu valorile
repartitiei Student pentru un nivel de semnificatie si (n-1) grade de libertate.
Daca ![]() <
<![]() se admite ipoteza diferentei nule.
se admite ipoteza diferentei nule.
Compararea dispersiilor necunoscute a doua esantioane de volum redus:
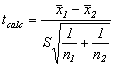
unde ![]()
Daca ![]() <
<![]() se admite ipoteza diferentei
nule. Pentru
se admite ipoteza diferentei
nule. Pentru ![]() numarul gradelor de libertate este
numarul gradelor de libertate este ![]() .
.
Pentru verificarea egalitatii dispersiilor a doua esantioane de volum redus folosim testul F (Fischer):
![]()
unde ![]() sunt estimatiile dispersiilor
teoretice
sunt estimatiile dispersiilor
teoretice ![]() si
si ![]() obtinute in doua sondaje
independente de volum
obtinute in doua sondaje
independente de volum![]() , respectiv
, respectiv ![]() .
.
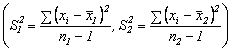
![]() se determina pentru nivelul de
semnificatie ales si pentru gradele de libertate
se determina pentru nivelul de
semnificatie ales si pentru gradele de libertate ![]() si
si ![]() . Daca
. Daca ![]() <
<![]() , nu avem motive sa
respingem ipoteza ca dispersiile sunt egale.
, nu avem motive sa
respingem ipoteza ca dispersiile sunt egale.
PROBLEME REZOLVATE
1. In vederea estimarii volumului desfacerilor zilnice prin unitati comerciale din orasul X, s-a efectuat o cercetare prin sondaj, pe baza unui esantion de 5% din unitatile comerciale din oras. Rezultatele sunt prezentate in tabelul nr. 2.
Repartitia unitatilor comerciale dupa volumul vanzarilor.
Tabelul nr.2
|
Grupe dupa volumul vanzarilor zilnice (mil. lei) |
120-140 |
140-160 |
160-180 |
180-200 | |
|
Numar de magazine |
Se cere: a) sa se calculeze eroarea limita maxima admisa;
b) sa se detemine intervalul de incredere pentru media vanzarilor si pentru volumul total al vanzarilor;
c) sa se redimensioneze volumul sondajului pentru o noua cercetare in urmatoarele conditii:
eroarea limita s-ar tripla,
eroarea limita s-ar reduce la 1/4 din nivelul actual al erorii.
Rezolvare: Se determina in prealabil media si dispersia seriei statistice prezentate in tabelul nr.3.
|
Grupe dupa volumul desfacerilor zilnice (mil.lei) |
Numar de magazine
|
Centru de interval
|
|
|
|
|
|
| ||||||
|
Total |
Notam si definim media volumului desfacerilor zilnice astfel:
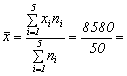 mil.lei.
mil.lei.
Dispersia esantionului este 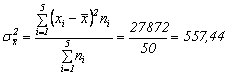
a) Eroarea medie de reprezentativitate:
pentru selectia repetata
![]() mil.lei.
mil.lei.
pentru selectia nerepetata: 5%N ![]() Þ 5%N
Þ 5%N ![]() Þ
Þ![]()
![]()
![]()
![]()
3,339.0,975![]() 3,2555 mil.lei.
3,2555 mil.lei.
Eroarea limita maxima admisa: se considera a Þ a ![]() Þ
Þ![]() si din tabelul functiei Laplace
se citeste za, care este
si din tabelul functiei Laplace
se citeste za, care este ![]() 1,96.
1,96.
pentru selectia repetata:
![]()
![]() 6,544 mil.lei.
6,544 mil.lei.
pentru selectia nerepetata:
![]() mil.lei.
mil.lei.
a) Intervalul de incredere pentru media volumului desfacerilor zilnice este in cazul unui risc de 5% :
pentru selectia repetata:
![]() <
<![]() <
<![]() U.M.
U.M.
< ![]() < 171,6
< 171,6![]() 6,544 mil.lei.
6,544 mil.lei.
< ![]() <
mil.lei.
<
mil.lei.
pentru selectia nerepetata:
171,6 - 6,382 < ![]() < 171,6
< 171,6![]() 6,382 mil.lei
6,382 mil.lei
165,218< ![]() < mil.lei.
< mil.lei.
Intervalul de incredere pentru volumul total al desfacerilor zilnice:
![]() U.M. Þ
U.M. Þ
pentru selectia repetata:
< ![]() < mil.lei.
< mil.lei.
165056 < ![]() < mil.lei
< mil.lei
pentru selectia nerepetata:
1000 < ![]() < mil.lei
< mil.lei
165218![]() 1000
1000![]() < mil.lei
< mil.lei
b) Daca eroarea limita s-ar tripla, atunci:
![]()
pentru selectia repetata ![]() 6,544
6,544![]() 19,632 mil.lei deci volumul esantionului este
19,632 mil.lei deci volumul esantionului este
![]() magazine;
magazine;
pentru selectia nerepetata ![]() 6,382
6,382![]() 19,146 mil.lei, deci volumul esantionului este:
19,146 mil.lei, deci volumul esantionului este:
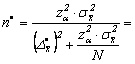
![]() magazine.
magazine.
Daca eroarea limita s-ar reduce la ![]() din nivelul actual,
atunci
din nivelul actual,
atunci ![]()
pentru selectia repetata ![]() 6,544
6,544![]() 1,636 mil.lei, deci volumul esantionului este
1,636 mil.lei, deci volumul esantionului este ![]() magazine;
magazine;
pentru selectia nerepetata ![]() si volumul esantionului ar fi
si volumul esantionului ar fi
![]() magazine.
magazine.
Se constata ca si intr-un caz si in celalalt, cresterea exigentei conduce la inregistrarea datelor dintr-un numar prea mare de magazine.
2. Pentru un esantion de 250
de agenti economici s-au obtinut urmatoarele rezultate: profitul mediu de 565
mil.lei/agent economic si abaterea medie patratica privind profitul: 66,4
mil.lei +tiind ca esantionul reprezinta 15% din totalul agentilor
economici, s-a format prin selectie nerepetata si rezultatele se garanteaza cu
o probabilitate de 0,9973 (![]() ), se cere:
), se cere:
a) estimarea profitului mediu si a profitului total la nivelul colectivitatii generale;
b) dimensionarea unui nou esantion daca eroarea limita maxima admisa este de 22 mil.lei.
Rezolvare:
a) Calculam in prealabil eroarea limita maxima admisa:
![]()
Din enuntul problemei se cunoaste ca n![]() agenti economici reprezinta 15% din N numarul total de agenti economici, deci
agenti economici reprezinta 15% din N numarul total de agenti economici, deci ![]()
![]()
![]()
![]() .
.
Se cunoaste abaterea medie patratica la nivelul esantionului,
deci putem determina dispersia esantionului ![]() Þ
Þ
![]() mil.lei.
mil.lei.
Profitul mediu al esantionului
este ![]() 565 mil.lei/agent economic, deci intervalul de incredere
pentru profitul mediu la nivelul intregii colectivitati este:
565 mil.lei/agent economic, deci intervalul de incredere
pentru profitul mediu la nivelul intregii colectivitati este: ![]() <
< ![]() <
< ![]() mil.lei/agent economic.
mil.lei/agent economic.
565 - 11,615![]()
![]()
![]() 565
565![]() 11,615 mil.lei/agent economic.
11,615 mil.lei/agent economic.
553,385 < ![]() < 576,615 mil.lei/agent
economic.
< 576,615 mil.lei/agent
economic.
Estimarea profitului total : ![]() mil.lei/agent economic.
mil.lei/agent economic.
Din ![]()
![]() agenti economici.
agenti economici.
1667 <![]() < mil.lei/agent economic,
< mil.lei/agent economic,
922492,795<![]() < mil.lei/agent economic.
< mil.lei/agent economic.
b)
Daca ![]() mil.lei, atunci volumul esantionului este:
mil.lei, atunci volumul esantionului este:
![]()
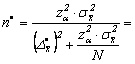
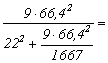
![]()
![]() 78,1 agenti
economici.
78,1 agenti
economici.
3. Pentru un esantion de 250 de agenti economici cunoastem repartitia bidimensionala dupa numarul de angajati si dupa marimea profitului , datele fiind prezentate in tabelul nr.4.
|
Grupe de agenti economici dupa numarul de angajati |
Grupe de agenti economici dupa marimea profitului (mil.lei) |
Total ni |
||||||
|
Sub 350 |
600 si peste |
|||||||
|
Sub 20 |
| |||||||
|
20 si peste | ||||||||
|
Total n j | ||||||||
+tiind ca esantionul reprezinta 10% din totalul agentilor economici si s-a format prin selectie repetata se cere:
a)
sa se estimeze intervalul de variatie al profitului mediu
si al profitului total in colectivitatea generala, garantand rezultatele cu o
probabilitate de 0,9973 (za![]()
b) sa se estimeze procentul maxim al agentilor economici cu un profit de cel putin 475 mil.lei.
Rezolvare:
a) Considerand repartitia agentilor economici dupa marimea profitului (mil.lei) determinam media esantionului:
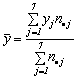 mil.lei, unde
mil.lei, unde ![]() sunt mijloacele
intervalelor de grupare.
sunt mijloacele
intervalelor de grupare.
![]()
![]()
![]() mil.lei/agent economic.
mil.lei/agent economic.
Dupa numarul de angajati esantionul este divizat in doua subgrupe I si II si vom calcula pentru fiecare grupa media si dispersia.
Algoritmul de calcul pentru medie si dispersie-grupa I sub 20 de angajati.
Tabelul nr.5
|
Grupe de ag.ec. dupa marimea profitului (mil.lei) |
Numar de angajati nIj |
Centre de interval yj |
|
|
|
|
|
8 |
2600 |
85747,6872 |
||||
|
6750 |
-53,53 |
2865,4609 |
51578,2962 |
|||
|
9350 |
-3,53 |
12,4609 |
274,1398 |
|||
|
46,47 |
2159,4609 |
73421,6706 |
||||
|
3 |
1575 |
96,47 |
9306,4609 |
27919,3827 |
||
|
Total |
Definim:
media 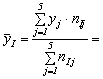
![]() 428,53 mil.lei/agent economic,
428,53 mil.lei/agent economic,
dispersia 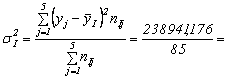
Algoritmul de calcul pentru medie si dispersie - grupa a II-a (numarul de angajati ³
Tabelul nr.6
|
Grupe de ag.ec. dupa marimea profitului (mil.lei) |
Numar de angajati nIIj |
Centru de interval yj |
|
|
|
|
|
7 |
2625 | |||||
|
25 |
-97,88 |
9580,4944 | ||||
|
31 |
-47,88 |
2292,4944 |
71067,3264 |
|||
|
37 |
2,12 |
4,4944 |
166,2928 |
|||
|
35 |
52,12 |
2716,4944 |
95077,3040 |
|||
|
30 |
102,12 | |||||
|
Total |
Definim:
media 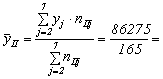 522,88 mil.lei/agent economic.
522,88 mil.lei/agent economic.
dispersia 
![]() 5283,379
5283,379
Calculam media dispersiilor de grupa, ca pe o medie arithmetica ponderata:
![]()
![]() 4442,79.
4442,79.
Eroarea limita maxima admisa este:
![]()
![]() 3,9992
3,9992
unde ![]()
Intervalul de variatie al profitului mediu:
![]() <
< ![]() <
< ![]() mil.lei/agent economic.
mil.lei/agent economic.
< ![]() < 490,8
< 490,8![]() 3,999 mil.lei/agent economic
3,999 mil.lei/agent economic
486,801< ![]() < mil.lei/agent economic.
< mil.lei/agent economic.
Estimarea profitului total, in
sensul precizarii intervalului de variatie al acestuia este: ![]() <
<![]() <
< ![]() mil.lei
mil.lei
![]()
Cum 10%N ![]() ag.ec. Þ
ag.ec. Þ ![]() ag.ec.
ag.ec.
2500.486,801< ![]() < mil.lei
< mil.lei
< ![]() < mil.lei.
< mil.lei.
b) Cerinta "procentul maxim al agentilor economici cu un profit de cel putin 475mil.lei" conduce la transformarea caracteristicii "profit" in caracteristica alternata cu doua forme de manifestare si obtinem datele prezentate in tabelul nr.7.
Distributia egentilor economici dupa numarul de angajati si marimea profitului.
Tabelul nr.7.
|
Grupe de ag. ec.dupa numarul de angajati |
Agenti economici cu profit < 475 mil.lei |
Agenti economici cu profit ³ 475 mil.lei (mi) |
Total (ni) |
|
|
|
Sub 20 | |||||
|
20 si peste | |||||
|
Total |
(n)s138 |
(n)s 250 |
(w)s0,552 |
Coloana 4 din tabelul nr.7 prezinta mediile de grupa si media pe total, iar coloana 5 prezinta dispersiile de grupa.
Calculam media dispersiilor de grupa:
![]()
![]() 0,1956.
0,1956.
Eroarea limita maxima admisa este:
![]() 0,0796
0,0796
Procentul maxim admis este:
![]() 0,552
0,552![]()
![]() sau 63,16%.
sau 63,16%.
Asadar, cel mult 0,6316.N![]() 0,6316.2500
0,6316.2500![]() 1579 din totalul agentilor economici din populatia
statistica generala au un profit de cel putin 475 mil.lei.
1579 din totalul agentilor economici din populatia
statistica generala au un profit de cel putin 475 mil.lei.
4. Pentru un numar de 120 unitati comerciale selectate aleator si nerepetat si care reprezinta 10% din numarul total al unitatilor, se cunosc urmatoarele date prezentate in tabelul nr.8.
Distributia unitatilor comerciale dupa numarul de angajati si valoarea vanzarilor.
|
Grupe de unitati comerciale dupa numarul de angajati |
Numarul unitatilor comerciale |
Valoarea medie a vanzarilor (mil.lei/unitate comerciala) |
|
Sub 20 | ||
|
40 si peste | ||
|
Total |
+tiind ca pe total unitati comerciale coeficientul de variatie a fost 22,5% se cere:
a) sa se determine intervalele de incredere in care se va incadra valoarea medie a vanzarilor si valoarea totala a vanzarilor stiind ca rezultatele se garanteaza cu o probabilitate de 0,9545 (za
b) sa se determine volumul esantionului daca eroarea limita ar creste cu 18,5%; sa se distribuie noul esantion pe subesantioane.
Rezolvare:
a) In tabelul nr.8 coloana 2 se prezinta valoarea medie a vanzarilor pe grupe de unitati comerciale dupa numarul de angajati, deci media esantionului se va determina ca medie ponderata a mediilor de grupa:
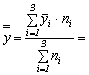
![]()
![]()
mil.lei/u.c.
Coeficientul de variatie la nivelul esantionului este:
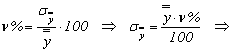
![]()
Þ ![]()
Calculul dispersiei dintre grupe :

![]()
![]()
![]() 92207,6389.
92207,6389.
Regula adunarii dispersiilor permite determinarea mediei dispersiilor de grupa:
![]() 185814,232313 - 92207,6389
185814,232313 - 92207,6389![]() 93606,593413
93606,593413
Eroarea limita admisa (![]() ) :
) :
![]()
![]()
mil.lei.
Valoarea medie a vanzarilor la nivelul tuturor unitatilor comerciale este:
![]() <
<![]() <
<![]() mil.lei/u.c.
mil.lei/u.c.
<![]() <1915,83
<1915,83![]() 52,99 mil.lei/u.c.
52,99 mil.lei/u.c.
<![]() < mil.lei/u.c.
< mil.lei/u.c.
Valoarea totala a vanzarilor este estimata astfel:
![]() <
<![]() <
<![]()
<![]() < mil.lei
< mil.lei
<![]() < mil.lei.
< mil.lei.
b) Eroarea limita creste cu 18,5%
Þ ![]()
![]() 52,99
52,99![]() 62,79315 mil.lei, volumul
62,79315 mil.lei, volumul
esantionului in aceste conditii este:
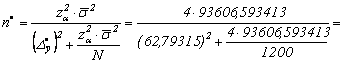
![]()
![]() 87,9 unitati
comerciale.
87,9 unitati
comerciale.
Volumul subesantioanelor luand in calcul
sondajul tipic nerepetat, ![]() unitati comerciale:
unitati comerciale:
selectie tipica neproportionala
![]() 29,3 unitati
comerciale.
29,3 unitati
comerciale.
selectie tipica proportionala.
Considerand ca esantionul utilizat respecta structura populatiei (grupa I 17%, grupa a II-a 58%, grupa a III-a 25%) atunci:
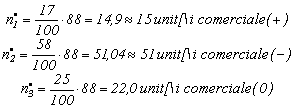
![]() u.c.
u.c.
5. Pentru evaluarea cheltuielilor suplimentare facute de turisti la sfarsit de saptamana intr-o statiune, pe durata a trei zile, s-a efectuat un sondaj stratificat iar datele inregistrate sunt prezentate in tabelul nr.9.
Cheltuielile medii zilnice si coeficientul de variatie in esantion
Tabelul nr.9
|
Grupe de turisti dupa varsta (ani) |
Numarul turistilor |
Cheltuieli suplimentare medii zilnice (mii lei) |
Coeficientul de variatie al cheltuielilor suplimentare (%) |
|
Sub 25 | |||
|
45 si peste | |||
|
Total |
Se cere:
a)
Considerand ca cele 350 de persoane reprezinta un
esantion stratificat de 5%, selectat in mod aleator si nerepetat din numarul
total al turistilor din statiune la sfarsit de saptamana, sa se determine intre
ce limite se vor incadra cheltuielile suplimentare medii si totale zilnice ale
turistilor din intreaga colectivitate, rezultatele fiind garantate cu o
probabilitate de 0,9545 (za![]()
b) Sa se stabileasca ce volum al esantionului ar fi fost necesar daca s-ar fi utilizat sondajul aleator simplu.
c) Sa se stabileasca ce volum de selectie va fi necesar daca se organizeaza o noua cercetare selectiva si eroarea limita admisa calculata la punctul a) se va mari cu 5%, celelalte conditii ramanand neschimbate.
Rezolvare:
a) Calculul indicatorilor de selectie si estimarea parametrilor colectivitatii generale:
media mediilor de grupa
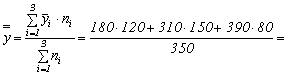 miilei/turist
miilei/turist
mii lei/turist
dispersiile de grupa (![]()
![]() i
i![]() 1,2,3, de
unde
1,2,3, de
unde ![]() , i
, i![]() 1,2,3
1,2,3
![]() 36 mii lei/turist Þ
36 mii lei/turist Þ ![]()
![]() 77,5 mii lei/turist Þ
77,5 mii lei/turist Þ ![]()
![]() 128,7 mii lei/turist Þ
128,7 mii lei/turist Þ ![]()
media dispersiilor de
grupa (![]() )
)
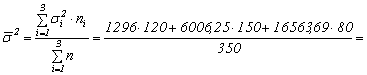
![]() 4490,150
4490,150
eroarea medie de
reprezentativitate (![]() ): 5%N
): 5%N ![]() 350 Þ
350 Þ
N![]() Þ N
Þ N![]() 7000
7000
![]()
![]() 3,4910 mii
lei
3,4910 mii
lei
eroarea limita admisa (![]() )
)
![]() 3491
3491![]() 6982 mii lei
6982 mii lei
estimarea cheltuielilor medii zilnice suplimentare pe total colectivitate:
![]() <
<![]() <
<![]() mii.lei/turist
mii.lei/turist
de unde :
<![]() <
< ![]()
< ![]() <
mii.lei/turist
<
mii.lei/turist
estimarea cheltuielilor zilnice suplimentare totale :
![]() <
<![]() <
<![]()
<![]() <
<
<![]()
![]() < mii lei.
< mii lei.
b) Determinarea volumului esantionului pentru sondajul aleator simplu nerepetat;
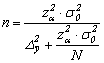
Deoarece nu cunoastem dispersia totala din colectivitatea generala ci numai datele despre esantionul format prin respectarea principiilor unei scheme probabilistice, putem inlocui acest indicator prin dispersia totala a datelor din esantion.
Dispersia totala a esantionului se determina in acest caz din regula de adunare a dispersiilor:
![]()

![]()
![]() 6566,20
6566,20
![]() 6566,2
6566,2![]() 4490,15
4490,15![]() 11056,35.
11056,35.
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 6777
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2025 . All rights reserved