Indicatori statistici - indicatori ai tendintei centrale, quartilele, indicatori ai variabilitatii, indicatori ai formei distributiei

INDICATORI STATISTICI

Notiunea de indicator si functiile indicatorilor

Cercetarea statistica a fenomenelor si proceselor socio-economice are ca obiectiv principal analiza aspectelor cantitative nemijlocit sesizabile pentru a afla si caracteriza esenta si calitatea acestora.

Definitie: Indicatorul statistic reprezinta expresia numerica a unor fenomene si procese social-economice, definite in timp, spatiu si structura organizatorica.17

Indicatorii statistici pot fi primari sau derivati.

Indicatorii primari exprima direct nivelul real de dezvoltare a caracteristicii cercetate, caracterizand fenomenul/procesul la modul cel mai general din punct de vedere cantitat Ei rezulta in urma observarii si centralizarii statistice a datelor individuale de masa, fie prin inregistrarea curenta, fie prin insumare partiala sau totala a datelor individuale de acelasi fel.

Indicatorii derivati se obtin prin prelucrarea marimilor absolute ale indicatorilor primari. Prelucrarea se face prin comparare, abstractizare, generalizare si alte procedee de calcul statistic.

Compararea se face prin diferenta sau prin raport. Prin diferenta se compara numai indicatorii absoluti cu acelasi continut si exprimati in aceeasi unitate de masura. Prin raport se pot compara indicatorii cu acelasi continut sau continut diferit, dar aflati in relatie de interdependenta.

1. INDICATORI AI TENDINTEI CENTRALE

Indicatorii tendintei centrale sunt indicatori sintetici cu ajutorul carora se exprima intr-o singura masura ceea ce este tipic, esential, stabil, obiectiv si caracteristic intr-o serie de date numerice.

Un indicator al tendintei centrale trebuie sa indeplineasca urmatoarele conditii:

sa fie definit in mod precis si obiectiv, eliminand aprecierea subiectiva a cercetatorului;

sa fie expresia tuturor observatiilor facute;

sa nu aiba caracter matematic prea abstract si sa posede proprietati simple si evidente;

sa poata fi calculat cu usurinta;

sa fie cat mai putin afectat de fluctuatiile de selectie (la extragerea mai multor esantioane dintr-o colectivitate generala, mediile sa nu fie sensibil diferite).

Indicatorii fundamentali ai tendintei centrale sunt: media aritmetica, modul si mediana.

1.1. Media aritmetica ()

Consideram ca termenul de medie este cel mai usor de inteles din intreaga statistica.

Au fost nenumarate situatiile in care am intalnit media: media la fizica pe trimestru sau semestru sa vedem daca am ramas corigenti sau am luat premiu, media

de la bacalaureat care ne ridica sau ne coboara sansele de admitere la facultate, la fel ca si media anilor de studiu sau media cheltuielilor zilnice care ne ajuta sa ne planificam mai bine bugetul.

Deci ce este media? Media aritmetica este indicatorul care se utilizeaza cel mai frecvent pentru caracterizarea tendintei centrale.

Media reprezinta valoarea care inlocuind toti termenii unei serii nu modifica nivelul totalizator si se calculeaza ca suma valorilor unei variabile raportata la numarul masuratorilor. Aceasta este media aritmetica, deoarece in statistica mai discutam si de media geometrica, media caracteristicilor alternative, media patratica, media rangurilor etc. Aceste concepte le intalnim insa mai rar in domeniul stiintelor socio-umane si prin urmare nu vom face decat sa le amintim.

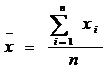(1) - pentru serie simpla

Exemplu: Varsta a 7 studenti de la facultatea de psihologie este de 25, 26, 32, 33, 40, 22, 26, 24. Varsta medie este :

In cazul in care datele au fost sistematizate intr-o serie de distributie de frecvente in care valorile/centrele intervalelor de variatie apar cu frecventele n_i, atunci media aritmetica, numita si medie aritmetica ponderata este:

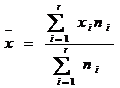(2) pentru o serie cu distributie de frecvente.

Exemplu : Salariile date angajatilor (mil. lei) de catre 70 de firme in anul 2005 a avut urmatoarea distributie:

Sa se calculeze media.

Raspuns : Fiind o serie cu distributie de frecvente vom aplica urmatoarea formula:

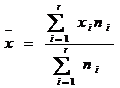unde:

X_i = centrul de interval

N_i =frecventa absoluta

Observam ca in formula avem si necunoscute, adica X_i (centrul de interval) si va trebui sa-l calculam.

X_i =

X_i =

X_i =

X_i =

Avand toate datele problemei, putem inlocui in formula, astfel :

→ Salariul mediu oferit este de 55 mil lei.

Nota: Pentru o serie de distributie de frecvente, media calculata pe baza frecventelor relative este egala cu media aritmetica determinata pe baza frecventelor absolute.

1.2. Modul (M₀ )

Modul este categoria cu frecventa cea mai mare, el reprezinta valoarea cel mai des intalnita intr-o serie statistica sau cea care are cea mai mare frecventa de aparitie. Modul se mai numeste si dominanta seriei sau valoarea modala.

Grafic, intr-o histograma ori poligon al frecventelor el reprezinta valoarea de pe abscisa corespunzatoare varfului reprezentarii.

In cazul datelor cantitative, in determinarea modului se tine cont de felul in care

acestea au fost sistematizate.

Pentru o serie statistica simpla de forma valoarea modala, M₀ = 32.

Pentru o serie de distributie de frecvente alcatuita dupa o variabila cantitantiva discreta, determinarea modului se face prin identificarea valorii careia ii corespunde frecventa maxima.

In cazul seriilor de distributie de frecvente pe intervale de variatie, determinarea modului presupune mai intai identificarea intervalului cu frecventa maxima:

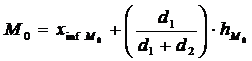
unde:

reprezinta limita inferioara a intervalului modal;

reprezinta marimea intervalului modal;

d₁ = diferenta dintre frecventa intervalului modal si a celui precedent;

d₁= ;

d₂ = diferenta din frecventa intervalului modal si a celui urmator;

d₂ =;

Daca d₁ = d₂ atunci modul va fi egal cu centrul intervalului modal.

O serie de date statistice poate sa aiba una sau mai multe valori modale. O distributie cu un singur mod se numeste unimodala, daca are doua valori dominante se numeste bimodala, iar daca are mai mult de doua moduri se numeste multimodala.

Exemplu : Salariile date angajatilor de catre 70 de firme in anul 2005 a avut urmatoarea distributie:

M₀ =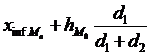

Int_mod = 50-60 (intervalul a carui frecventa absoluta este cea mai mare)

= 50

d₁ =

= frecventa intervalului modal

= frecventa intervalului anterior celui modal

d₁ = 25 15 = 10

d₂ =

= frecventa intervalului modal

= frecventa intervalului urmator celui modal

d₂ = 25 - 10 = 15

M_o =58

1.3. Mediana (M_e)

Mediana este o alta masura a tendintei centrale si reprezinta valoarea care imparte sirul de masuratori in doua parti egale; jumatate din sirul de date vor avea valori mai mici decat mediana in timp ce cealalta jumatate vor avea valori mai mari decat mediana.

Mediana este un indicator mediu de pozitie, care face parte din categoria cuartilelor. Ea prezinta valoarea/varianta din mijlocul unei serii de date, serie in care observatiile au fost ordonate crescator (sau descrescator). Mediana este situata in centrul (mijlocul) seriei.

Mediana poate fi folosita in caracterizarea tendintei centrale pentru o serie de date masurate pe o scala ordinala. Mediana ia in considerare doar pozitia observatiilor in serie, nu si magnitudinea lor efectiva.

Pentru a determina mediana introducem notiunea de ranguri, adica, numere de ordine asociate observatiilor (cea mai mica rang 1; cea mai mare rang n).

Locul medianei (Loc_Me) va fi rangul unitatii din mijlocul distributiei.

Loc_Me =

Pentru seriile simple la determinarea valorii din mijloc trebuie sa luam in consideratie situatiile:

a)          Daca n este un numar impar

pentru date cantitative mediana este exact valoarea din mijlocul seriei

Exemplu: In cazul unui sir impar, mediana este valoarea de la mijlocul unui sir. Daca reluam exemplul anterior, si mai adaugam un scor, obtinem:

Sirul are 7 valori. Ordonand sirul, obtinem:

De data aceasta, la mijlocul acestui sir gasim valoarea 17, valoarea medianei.

Observam ca n = 7.

Loc_Me = =

Loc_Me =4 → a 4-a valoarea din sirul de numere ordonate crecator sau descrescator reprezinta mediana → Me =17

Ordonand un sir, putem preciza pozitia fiecarui element in cadrul acelui sir.

Altfel spus, mediana nu este altceva decat pozitia rangului din mijloc in sirul ordonat de date. Intr-o serie de la 1 la 7, pozitia din mijlocul sirului este evident, pozitia 4. Acesta este de altfel si locul in care gasim mediana.

b)     Daca n este un numar par, exista doua valori situate in mijlocul seriei.

daca datele sunt cantitative, mediana este media celor doua valori din mijloc

Exemplu: Se considera urmatorul sir de date:

Pentru a calcula mediana, primul pas este acela de a ordona crescator sau descrescator aceste date. Ordonand crescator sirul de mai sus, obtinem:

Sa se calculeze mediana.

Se ordoneaza datele crescator, astfel : 10, 15, 18, 20, 21, 22.

Loc_Me = = mediana se situeaza intre a treia si a patra valoare din serie.

Me =

Dupa definitia medianei, in cazul nostru avem 6 valori. Prin urmare, mediana va fi valoarea care imparte acest sir ordonat in doua parti egale. Fiind 6 valori, mediana este situata la limita primelor 3 valori. Deoarece sirul este un sir par, mediana se situeaza, in cazul nostru, intre valoarea 18 si valoarea 20, mai precis la valoarea 19.

c. Pentru o serie de distributie de frecvente variate determinarea medianei presupune calcularea mai intai a frecventelor cumulate. Prima frecventa cumulata mai mare decat (n+1)/2 (locul medianei) ne indica varianta mediana

Exemplul 1: Pentru 80 de familii dintr-un bloc s-au sistematizat date privind numarul membrilor de familie, rezultand distributia:

Loc_Me =

adica, intre a 40-a si a 41-a familie prima frecventa cumulata mai mare decat 40,5 este 65 varianta trei membrii de familie reprezinta varianta mediana situata in mijlocul distributiei.

Pentru o serie de repartitie de frecvente pe intervale de variatie, mediana se va incadra in intervalul median, primul interval cu frecventa cumulata mai mare decat Loc_Me.

Exemplul 2: Se da distributia:

Loc_Me = ; n = 90

M_e =

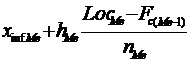
unde:

- limita inferioara a intervalului median

h_Me marimea intervalului median

F_c(Me-1) - frecventa cumulata a intervalului anterior celui median

n_Me frecventa absoluta a intervalului median

M_e = 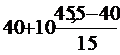= 43,66

M_e = 43,66

Mediana prezinta unele avantaje fata de medie:

este mai putin afectata de valorile extreme, luand in considerare doar pozitia valorilor nu si magnitudinea lor efectiva;

poate fi folosita intr-o distributie pe intervale chiar si in cazul in care primul sau ultimul interval sunt deschise;

este un indicator ce poate fi folosit si pentru date ordinale;

Dezavantajele medianei:

mediana nu poate fi supusa la fel de usor calculelor algebrice;

media este preferabila in procesul de inferenta statistica.

2. QUARTILELE

Quartilele impart seria in patru parti egale, ele delimitand cele 25% din observatii. Quartilele sunt in numar de trei: Q₁, Q₂, Q₃.

Q₁ este cuartila inferioara;

Q₂ este egala intotdeauna cu mediana;

Q₃ este cuartila superioara;

Determinarea valorilor quartilelor se face adoptand formulele medianei:

Q₁ =

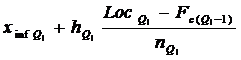
unde:

= limita inferioara a intervalului quartilic;

= marimea intervalului quartilic;

= ;

= locul quartilei, primele 25% valori;

= frecventa cumulata a intervalului anterior celui quartilic;

= frecventa absoluta a intervalului quartilic;

;

;

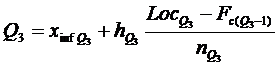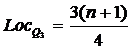= locul quartilei, ultimele 25% din valori;

Exemplul 1: Salariile date angajatilor de catre 70 de firme in anul 2005 a avut urmatoarea distributie:

Q₁ =

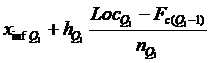
Intervalul primul interval care are frecventa cumulata mai mare decat locul quartilei Q₁

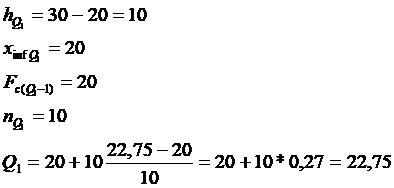
Q₃ = primele 25% din firmele care ofera cele mai mari salarii.

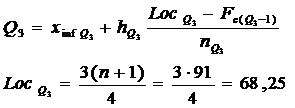
Intervalul quartilei Q₃ =

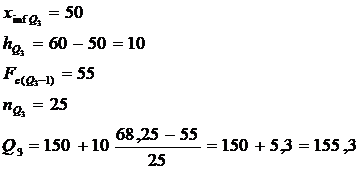
Q₃= 155,3 → primele 25% din firmele care ofera cele mai mici salarii.

3. INDICATORI AI VARIABILITATII

Din aceasta grupa fac parte:

amplitudinea variatiei (absoluta si relativa);

abaterile individuale (absolute si relative).

Amplitudinea absoluta (A) se calculeaza ca diferenta intre nivelul maxim si nivelul minim al caracteristicii.

A = x_max - x_min

Amplitudinea relativa a variatiei (A_%) se exprima in procente si se calculeaza ca raport intre amplitudinea absoluta a variatiei si nivelul mediu al caracteristicii.

A_% =

Amplitudinea se foloseste la controlul calitatii produselor prezentand importanta si din punct de vedere metodologic, fiind folosit in prima faza a prelucrarii statistice la stabilirea numarului de grupe si a marimii intervalului de grupare.

3.1. Indicatorii sintetici ai variatiei

Indicatorii sintetici ai variatiei trebuie sa se bazeze pe toate observatiile, sa fie usor de calculat, cat mai putin afectati de fluctuatiile de selectie daca datele provin dintr-o cercetare statistica partiala pentru care trebuie verificata si reprezentativitatea esantionului.

Indicatorii sintetici ai variatiei sunt:

abaterea medie liniara;

abaterea medie patratica;

dispersia;

conflictul de variatie.

3.1.1. Abaterea medie liniara ()

Se mai numeste variatie medie, deviatie medie, abatere absoluta medie sau abatere liniara medie si se poate calcula atunci cand media este un bun indicator al tendintei centrale. Acest indicator informeaza asupra modului in care se abat, in valori absolute, rezultatele de la medie, acordand aceeasi pondere tuturor variabilelor. Abaterea medie se poate calcula pe date grupate sau pe date discrete.

Se calculeaza ca medie aritmetica simpla sau ponderata a abaterilor termenilor seriei de la media lor, luata in valoare absoluta.

Pentru o serie simpla:

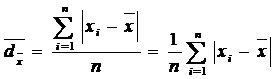
Pentru o serie de distributie de frecvente absolute:

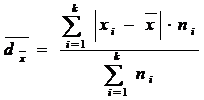
Pentru o serie cu frecvente relative, exprimate in procente:

.

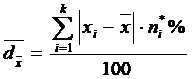Exemplu:

Pentru 200 de persoane s-au sistematizat datele culese cu privire la timpul zilnic petrecut in fata televizorului rezultand:

T=5199

Sa se calculeze abaterea medie liniara.

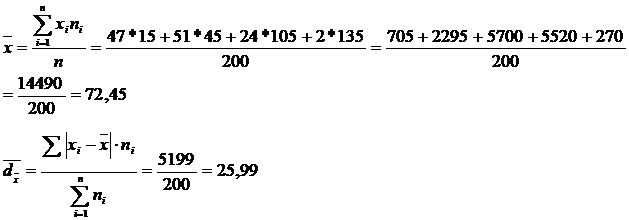
3.1.2. Dispersia (varianta) unei caracteristici ()

Atunci cand putem utiliza media, un indicator frecvent este indicatorul dispersiei sau indicatorul variantei (atentie, nu variatie ci varianta) notat cu sigma patrat pentru populatie sau s² in cazul unui esantion.

Se calculeaza ca medie aritmetica simpla sau ponderata a patratelor abaterilor termenilor seriei fata de media lor.

Formula de calcul a dispersiei este urmatoarea, in care x_i reprezinta valoarea masurata, x barat media iar N numarul de masuratori.

- pentru o serie simpla

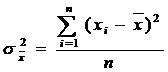
pentru o serie cu frecvente absolute

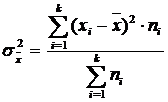
pentru o serie cu frecvente relative, exprimate in procente

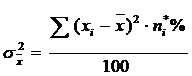
Exemplu: Pentru 200 de persoane s-au sistematizat datele culese cu privire la timpul zilnic petrecut in fata televizorului rezultand:

T=11490 T=182299

Sa se calculeze dispersia.

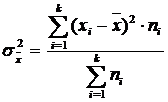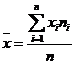,=57,45

3.1.3. Abaterea medie patratica (abaterea tip sau abaterea standard)

Se noteaza cu s in cazul unui esantion sau cu sigma in cazul unei populatii si o putem intalni sub numele de abatere etalon, abatere tip, abatere patratica medie. Acest indicator este cel mai precis si inteligibil pentru masura gradului de imprastiere

a rezultatelor in jurul tendintei centrale si contribuie la definirea distributiei normale. Poate fi calculat si dobandeste semnificatie numai atunci cand poate fi calculata media.

Se calculeaza ca medie patratica a abaterilor tuturor variantelor seriei de la media lor aritmetica si se noteaza .

Relatiile de calcul ale abaterii mediei patratice sunt:

pentru o serie simpla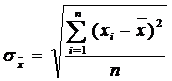

Daca privim cu atentie aceasta formula, constatam ca expresia de sub radical nu este altceva decat varianta. Prin urmare, dupa ce calculam varianta, putem afla usor abaterea standard extragand radicalul de ordin doi din varianta.

pentru o serie de frecvente absolute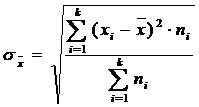

pentru o serie de frecvente relative, exprimate in procente

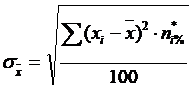
Exemplu:

30.19 minute

3.1.4. Coeficientul de variatie ()

Prezinta, mai intuitiv decat abaterea standard, gradul de imprastiere al rezultatelor in jurul mediei, deoarece este o expresie procentuala a impartirii abaterii standard la medie.

Se calculeaza ca raport intre abaterea medie patratica si nivelul mediu al seriei, deoarece abaterea standard se foloseste frecvent pentru masurarea abaterii medii.

Formula de calcul este:

sau (daca s-a calculat abaterea medie liniara )

Cu cat nivelul lui este mai apropiat de zero cu atat variatia este mai redusa, colectivitatea este mai omogena, media avand un grad mai ridicat de reprezentativitate; cu cat valoarea sa este mai departe de zero, cu atat variatia este mai intensa, colectivitatea mai eterogena, iar media are un nivel de semnificatie mai scazut.

4. INDICATORI AI FORMEI DISTRIBUTIEI

In cazul variablelor continue ce pot fi sistematizate in distributii de frecvente cu ajutorul intervalelor de grupare pe langa determinarea indicatorilor tendintei centrale si variabilitatii se pune problema sa studiem si modul in care valorile individuale sunt deplasate si centralizate comparativ cu tendinta centrala.

Forma unei distributii de frecvente se analizeaza comparativ cu distributia ideala, normala prin indicatori asimetrici (oblicitatii) si indicatori ai boltirii (excesului).

4.1. Indicatori ai asimetriei (oblicitatii)

Asimetria se observa prin reprezentarea grafica prin histograma sau poligonul frecventelor, dar poate sa fie masurata prin indicatori specifici.

Distributiile de frecvente pot fi:

perfect simetrice: (fig. 1a);

cu asimetrie pozitiva: (fig. 1b);

cu asimetrie negativa: (fig. 1c).

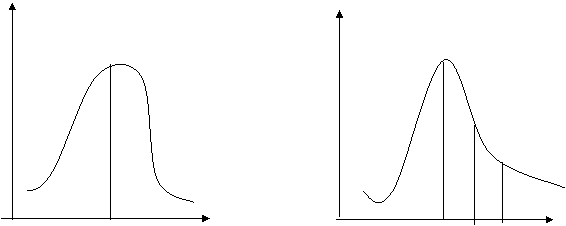
Fig.1 fig.2

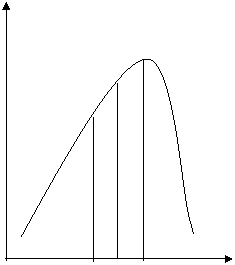
Fig.3

Asimetria in valoarea absoluta se poate masura cu indicatorii:

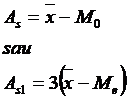
Dar o distributie este caracterizata si prin variabilitatea datelor. O serie care are variabilitatea mai mica va fi mai pronuntata oblica, iar intr-o serie mai imprastiata oblicitatea se va atenua. Pentru aceasta vom calcula coeficientul de asimetrie Pearson:

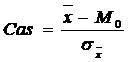coeficientul care ia valori pozitive in cazul curbelor alungite spre dreapta (asimetrie pozitiva) si valori negative in cazul curbelor alungite spre stanga (asimetrie negativa).

Coeficientul de asimetrie este nul pentru o distributie simetrica. El mai poate fi exprimat: .

Exemplu:

Presupunem ca pentru 200 de persoane s-au sistematizat datele culese cu privire la timpul zilnic petrecut in fata televizorului, rezultand:

T=11490

Mo =x_infMo-h_Mo

M_o=60+30

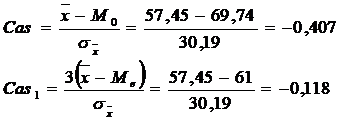ceea ce semnifica o asimetrie negativa moderata (coada mai lunga a distributiei tinde spre valori mici).

4.2. Coeficientul Yule

Coeficientul masoara gradul de asimetrie prin raportul dintre diferenta si suma abaterilor quartile si se calculeaza dupa formula alaturata. Observam ca, pentru a calcula acest coeficient, este necesar sa calculam pur si simplu cele trei quartile, dupa metoda prezentata intr-unul dintre capitolele anterioare.

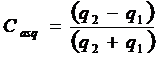unde Q₁= M_e-Q1

Q₂=Q₃-M_e

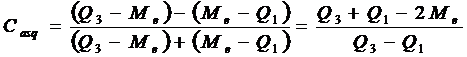
Coeficientul poate lua, in general, valori de la -1 la +1 si indica marimea asimetriei negative sau pozitive. Cu cat valorile sunt mai apropiate de 0, cu atat distributia este mai simetrica. Cu cat se apropie de -1 sau de +1, ea devine tot mai asimetrica spre stanga sau spre dreapta.

Acest coeficient este foarte usor de calculat, insa tine cont doar de cateva valori valorile quartile si nu de toate valorile din distributie, fapt care ii limiteaza precizia si se considera ca este doar un coeficient elementar al simetriei.

Exemplu:

Pentru o distributie s-au stabilit urmatoarele rezultate:

Q₁= 150

M_e= 130

Q₃=140.

Sa se calculeze valoarea coeficientului de asimetrie Yule.

Raspuns. Coeficientul de asimetrie yule se calculeaza dupa relatia:

C_asq= = = = = -3

Q₁= M_e-Q1=130-150= -20

Q₂=Q₃-M_e= 140-130= 10

Interpretare: Valoarea obtinuta, C_asq= -3<0 arata ca distributia considerata este asimetrica la stanga.

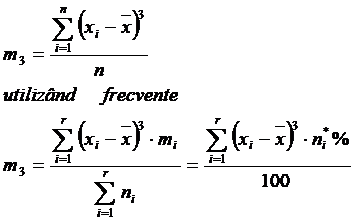Analiza oblicitatii (asimetriei)se poate face si pe baza momentelor centrate de ordinul 3:

Daca seriile de distributie cu asimetrie negativa sunt mai numeroase, valorile x_i mai mici decat media, atunci abaterile sunt negative.

Daca seriile de distributie au asimetrie pozitiva sunt mai numeroase valorile x_i mai mari decat media, atunci abaterile sunt pozitive.

Daca seriile de distributie sunt perfect simetrice, abaterile pozitive sunt tot atat de numeroase ca si cele negative.

O marime relativa a asimetriei se obtine prin raportarea la abaterea medie patratica ridicata la cub.

4.3. Coeficientul de asimetrie Fisher

Coeficientul de asimetrie Fisher, nu se bazeaza pe cateva elemente, precum coeficientul Yule, ci pe toate valorile din distributie si se calculeaza folosindu-se momentele centrate.

Coeficientul de asimetrie (Fisher): .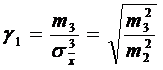

Sau

Coeficientul γ₁ va avea valoare mai mare decat zero in cazul asimetriei pozitive, valoare mai mica decat zero in cazul asimetriei negative si va fi egal cu zero in cazul seriei perfect simetrice.

Atunci cand discutam de asimetrie, trebuie sa precizam o serie de relatii care apar intre indicatorii tendintei centrale, media, mediana si modulul.

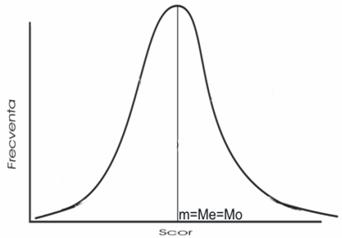
Intr-o distributie simetrica, media, mediana si modul au exact aceleasi valori.

Caracteristica acestei distributii o reprezinta coincidenta absoluta a celor trei indicatori ai tendintei centrale. Dupa cum puteti observa in figura de mai sus, atat media, cat si mediana si modul, se afla in acelasi punct, la mijlocul distributiei.

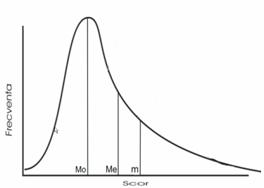Intr-o distributie asimetrica la dreapta (distributie skewness pozitiv, vezi figura alaturata), predomina scorurile mici. In acest caz, modulul este valoarea situata cel mai la stanga in sirul de date, iar mediana este mai mare decat media. Evident, mediana fiind valoarea care imparte sirul ordonat de date in doua parti egale, iar daca in distributie predomina scorurile mici, atunci scorurile mari sunt considerate ca scoruri extreme. Stim, de la analiza preciziei indicatorilor tendintei centrale, ca intr-o serie de date in care intalnim scoruri extreme mari, media tinde sa le puna in valoare. Iata ca acest fapt este ilustrat grafic in figura de mai sus. Observati relatia existenta intr-o asemenea distributie: Mo<Me<m. Aceasta relatie este relatia caracteristica a unei distributii asimetrice pozit

Intr-o distributie asimetrica la stanga (distributie skewness negativ, vezi figura alaturata), predomina scorurile mari. In acest caz, modul este valoarea situata cel mai la dreapta in sirul de date, iar mediana este mai mare decat media. Evident, mediana fiind valoarea care imparte sirul ordonat de date in doua parti egale, iar daca in distributie predomina scorurile mari, atunci scorurile mici sunt considerate ca scoruri extreme.

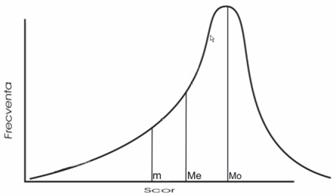Stim, de la analiza preciziei indicatorilor tendintei centrale, ca intr-o serie de date in care intalnim scoruri extreme mici, media tinde sa le puna in valoare. Iata ca acest fapt este ilustrat grafic in figura de mai sus in care se observa relatia existenta.

Intr-o asemenea distributie: Mo>Me>m. Aceasta relatie este relatia caracteristica a unei distributii asimetrice negat

4.4. Boltirea

Boltirea masoara inaltimea, adica alungirea sau aplatizarea curbei, comparativ cu cea normala.

Asimetria pe orizontala, presupune, dupa cum am vazut, o deplasare a tendintei centrale spre stanga sau spre dreapta, catre scoruri mici sau catre scoruri mari. Aceasta este singura asimetrie posibila? Ei bine, nu. Exista si un fel de asimetrie verticala sau boltire.

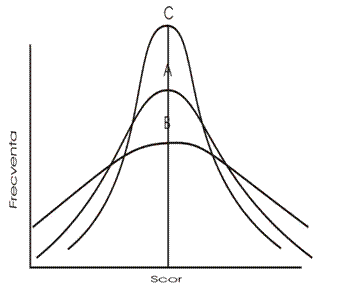
Termenul folosit generic pentru acest concept este termenul de kurtosis (din limba greaca, kurtos = cocosat). Practic, boltirea se refera la aspectul cocoasei distributiei rezultatelor.

Cocoasa poate fi ascutita si atunci vorbim de o distributie ascutita sau leptocurtica, poate fi turtita, distributia turtita, plata sau platicurtica sau normala, distributie mezocurtica. O distributie normala este intotdeauna o distributie mezokurtica.

In figura de mai sus, distributia C este o distributie leptocurtica, ascutita. Distributia B este o distributie platicurtica, turtita, iar distributia A este o distributie normala sub aspectul boltirii, sau mezocurtica.

distributie leptocurtica, ascutita, arata ca datele sunt foarte grupate si apropiate de medie, lotul de subiecti avand un mare grad de omogenitate a scorurilor

O distributie platicurtica, plata, este o distributie in care rezultatele sunt foarte imprastiate fata de medie si indica un grad ridicat de eterogenitate a scorurilor.

Ati observat deja ca boltirea nu este altceva decat simetria pe axa verticala (O_Y), spre deosebire de simetria propriu zisa, deplasarea valorilor pe axa orizontala (O_X).

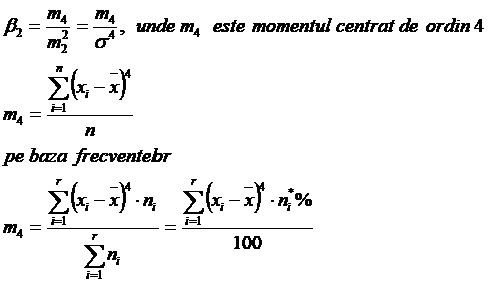
Pentru curba normala (serie simetrica) β₂ = 3. Daca β₂ > 3, curba este mai ascutita decat cea normala (distributie leptocurtica). Daca β₂ < 3, curba este mai turtita decat cea normala (dispozitie platicurtica).

Boltirea se mai poate masura si cu indicatorul: 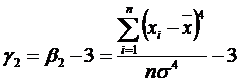, care va avea valoarea zero daca distributia este normala, valoare pozitiva pentru distributie leptocurtica si valoare negativa pentru distributie platicurtica.

Exemplu: Distributia a 380 de firme dupa numarul de zile de asteptare pana la realizarea fuzionarii este:

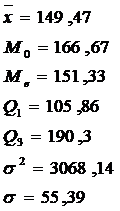
Sa se calculeze oblicitatea si excesul repartitiei.

Rezolvare:

a. Coeficientul Yule

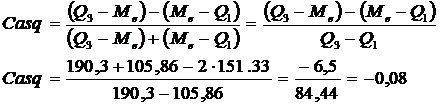
Asimetria este negativa moderata.

(Oblicitatea cu ajutorul momentelor centrate de ordinul 3 )

b. Boltirea

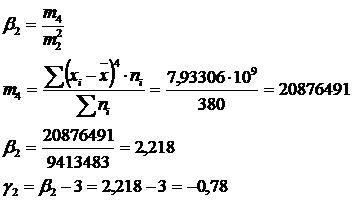
Curba este slab platicurtica (aplatizata) deoarece

Momentele de ordin r sunt valori ale caractersiticii urmarite care impart distributai observatiilor in r parti egale si au acelasi efectiv 1/r din numarul unitatilor .

Exemplu: mediana = quartila 2 = moment de ordin 2

quartila = quartila de ordin 4

5. Alegeti raspunsul corect

1. Media aritmetica, ca indicator fundamental al tendintei centrale:

a)     reprezinta valoarea care modifica nivelul totalizator al seriei;

b)     se foloseste cel mai frecvent si reprezinta suma valorilor raportata la numarul lor;

c)     se calculeaza adunand valorile existente;

d)     nu poate determina numarul de unitati din colectivitate.

2. Media aritmetica reprezinta:

a) valoarea pe care ar purta-o fiecare unitate statistica daca distributia ar fi eterogena;

b) valoarea pe care ar purta-o fiecare unitate statistica daca distributia ar fi omogena;

c) valoarea pe care ar purta-o fiecare variabila statistica daca distributia ar fi omogena.

3. Media aritmetica a unei sume dintre doua variabile este egala cu suma mediilor celor doua variabile, cand:

a)     cele doua variabile se afla intr-o relatie de interdependenta;

b)     cele doua variabile se afla intr-o relatie de inversa proportionalitate;

c)     cele doua variabile se refera la aceeasi colectivitate;

d)     cele doua variabile sunt independente;

e) cele doua variabile sunt direct proportionale.

4. Care dintre urmatoarele afirmatii privind media aritmetica este adevarata:

a)     suma patratelor tuturor abaterilor individuale ale termenilor seriei de la media lor aritmetica este zero;

b)     marimea mediei aritmetice este cuprinsa intre x_min si x_max doar daca seria prezinta o tendinta clara de asimetrie;

c)     pentru o serie de distributie de frecvente, media aritmetica, calculata pe baza frecventelor reduse de c ori, este mai mica decat media seriei initiale de c ori;

d)     media produsului a doua variabile aleatoare este egala cu produsul mediilor celor doua variabile;

e)     pentru o serie de distributie de frecvente, media calculata pe baza frecventelor relative este egala cu media aritmetica determinata pe baza frecventelor absolute.

5. Mediana, ca indicator statistic:

a) prezinta valoarea din mijlocul unei serii de date in care observatiile au fost ordonate crescator sau descrescator;

b) nu poate fi folosita in caracterizarea tendintei centrale pentru o serie de date masurate pe o scala ordinala;

c) nu are nici o legatura cu notiunea de rang.

6. 25% din salariatii unei inteprinderii au un salariu de cel mult 4 milioane lei. Aceasta valoare reprezinta:

a) quartila unu;

b) mediana;

c) quartila trei.

7. 75% din salariatii unei intreprinderii au un salariu de cel mult 7 milioane lei. Aceasta valoare reprezinta:

a) quartila unu;

b) mediana;

c) quartila trei.

8. 50% din salariatii unei intreprinderii au un salariu de cel mult 5 milioane lei. Aceasta valoare reprezinta:

a) quartila unu;

b) mediana;

c) quartila trei.

9. Intr-o repartitie normala valoarea fata de care 25% din valorile individuale sunt mai mici iar 25% din valorile individuale sunt mai mari este:

a. cuartila a doua;

b. cuartila a treia;

c. cuartila intai;

d. valoarea modala.

10. Media este o marime generalizata, adica, inlocuind fiecare nivel individual al caracteristicii de distributie cu nivel mediu:

a. suma termenilor seriei ramane aceeasi;

b. suma termenilor seriei se modifica;

c. suma termenilor seriei este nula.

11. Varianta (dispersia) de grupa masoara:

a) variatia sub influenta factorilor aleatori (variatia reziduala)

b) variatia sub influenta factorilor esentiali

c) variatia sub influenta factorilor aleatori si esentiali

12. Daca dorim sa obtinem un indicator al tendintei centrale pentru date masurate pe orice scala, vom determina:

a)     media aritmetica;

b)     modul;

c)     media geometrica;

d)     media ponderata.

13. Modul se afla dupa relatia:

a) M_o = x_i - h_Mo * ;

b) M_o = x_i + h_Mo * ;

c) M_o = x_i-1 h_Mo

14. Care dintre urmatoarele variante nu reprezinta un indicator al tendintei centrale?

a)     mod;

b)     distributie de frecvente;

c)     mediana;

d)     medie;

e)     medie ponderata.

15. Daca dorim sa obtinem un indicator al tendintei centrale care sa nu fie afectat de valorile extreme, sa poata fi calculat pentru date masurate pe orice scala (cu exceptia celei nominale) si sa aiba o singura valoarea, vom calcula:

a)     media aritmetica

b)     modul;

c)     media geometrica;

d)     mediana;

e)     media ponderata.

16. Modul se utilizeaza pentru caracterizarea:

a. tendintei generale si gradului de asimetrie;

b. gradului de boltire;

c. gradului de concentrare.

17. Quartilele sunt marimi de pozitie care impart colectivitatea in:

a. n-1 parti egale;

b. 4 parti egale;

c. 5 parti egale;

18. In distributia de mai jos:

Intervalul (15 20) reprezinta:

a.     intervalul median;

b.     intervalul modal;

c.      intervalul quartilic.

19. Rolul indicatorilor tendintei centrale ai unei distributii statistice este de a:

a) sintetiza datele

b) calcula marimile relative

c) aprecia gradul de dispersie al colectivitatii.

20. Asimetria se calculeaza dupa relatia:

a) A_s= Mo

b) A_s= 3(-Me)

c) A_s= 2(-Mo)

21. Coeficientul de asimetrie Yule, se calculeaza dupa relatia:

a) C_asq= ; unde: Q₁= M_e-Q₁

Q₂=Q₃-M_e

a)                         b) C_asq=

b)                         c) C_asq=

22. Coeficientul de boltire se calculeaza dupa relatia:

a) β₂= _c) β₂=

b) β₂=

23. O distributie este mezocurtica atunci cand:

a) β₂ = 3, γ₂ = 0

b) β₂ > 3, γ₂ >0

c) β₂ < 3, γ₂ < 0

24. O distributie este leptocurtica atunci cand:

a) β₂ = 3, γ₂ = 0

b) β₂ > 3, γ₂ > 0

c) β₂ < 3, γ₂ < 0

25. O distributie este platicurtica atunci cand:

a) β₂ = 3, γ₂ = 0

b) β₂ > 3, γ₂ >0

c) β₂ < 3, γ₂ < 0

26. Abatarea medie liniara se calculeaza dupa relatia:

a) c)

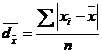
b)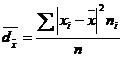

27. Coeficientul se utilizeaza pentru analiza statistica a:

a)     asimetriei;

b)     variatiei;

c)     boltirii;

d)     tendintei centrale;

e)     indicatorilor medii de pozitie.

28. Intr-o serie de repartitie pe intervale formata dupa o anumita variabila, valoarea sa modala este influentata de:

a) limitele inferioare si superioare ale intervalelor extreme;

b) de frecventele de aparitie ale intervalelor egale sau neegale;

c) de marimea egala sau neegala a intervalelor de variatie;

d) de limita inferioara a intervalului modal;

e) de limita inferioara, de frecventele intervalului modal, premodal si postmodal;

6. Probleme

1. Valoarea vanzarilor inregistrate de firma A pe parcursul a sapte (7)

zile, se prezinta astfel (in milioane lei) : 200, 250, 750, 1001, 1520, 1800, 2300.

Sa se calculeze valoarea medie zilnica a vanzarilor realizate de firma A.

2. Distributia dupa volumul vanzarilor zilnice (milioane lei) a unitatilor comerciale dintr-un judet in luna Ianuarie 2004, se prezinta astfel:

-

Sa se calculeze nivelul mediu al vanzarilor zilnice.

3. Se da urmatoarea distributie:

Sa se calculeze modul.

4. O firma inregistreaza, intr-o perioada de 5 zile, urmatoarele date privind volumul vanzarilor (milioane lei) : 5, 7, 20, 14, 9.

- sa se afle valoarea medianei (locul medianei)

5. O firma inregistreaza, intr-o perioada de 6 zile, urmatoarele date privind volumul vanzarilor (milioane lei) : 10, 40, 20, 15, 22, 35.

- sa se afle valoarea medianei .

6. Distributia familiilor dintr-un bloc dupa numarul de copii se prezinta astfel:

Sa se calculeze valoarea medianei.

7. . Distributia muncitorilor unei firme dupa timpul consumat pentru realizarea produsului A, se prezinta astfel:

Sa se calculeze valoarea medianei.

8. Distributia muncitorilor unei firme dupa timpul consumat, pentru realizarea produsului A se prezinta astfel:

Sa se calculeze valoarea quartelei unu.

9. Distributia muncitorilor firmei A dupa timpul consumat pentru realizarea produsuluiX se prezinta astfel:

Sa se calculeze valoarea quartilei trei.

10. Distributia unui esantion de firme dupa cifra de afaceri lunara, X, in mil lei, in anul 2004, este prezentata astfel:

Sa se calculeze abaterea medie liniara.

11. . Daca: Q₁= 128,13 mil. lei

M_e= 137,86 mil. lei

Q₃= 147,92 mil. lei

Atunci, coeficientul de asimetrie Yule este egal cu:

a)       141 si arata o distributie simetrica

b)      0, 016 si arata o distributie moderat asimetrica

c)       0,016 si arata o distributie puternic asimetrica.

12. Pentru o distributie s-au stabilit urmatoarele rezultate:

Q₁= 150

M_e= 130

Q₃=140.

Sa se calculeze valoarea coeficientului de asimetrie Yule.

13. Pentru o distributie s-au obtinut urmatoarele rezultate:

m₄ = 40.000 ; m₂ = 100.

Sa se calculeze valoarea coeficientului de boltire.

14. Daca: m₄ = 54059,44

m₂ = 162,6

atunci coeficientul de boltire si interpretarea sa corecta sunt:

a)          β = 2,045 → arata o distributie usor platicurtica;

b)         β = 2,045 → arata o distributie usor leptocurtica;

c)          β = 2,045 → arata o distributie usor mezocurtica.

15. Pentru o distributie s-au obtinut urmatoarele rezultate:

M_o = 125 minute

= 130 minute

= 12 minute.

Sa se calculeze valoarea coeficientului empiric de asimetrie Pearson.

16. Distributia unui esantion de firme dupa cifra de afaceri lunara X, in milioane lei, in anul 2004, este:

Sa se calculeze variatia (dispersia).

17. Pentru o distributie statistica s-a obtinut o valoare a coeficientului de boltire egala cu 2,5.

Sa se calculeze coeficientul Fisher.

18. Distributia unui esantion de firme dupa cifra de afaceri lunara, X, in mil. lei, in anul 2006, este:

Sa se calculeze valoarea coeficientului de variatie.

	7. Raspunsuri corecte

5. Raspunsuri corecte.

1. b - se foloseste cel mai frecvent si reprezinta suma valorilor raportata la numarul lor;

2. b - valoarea pe care ar purta-o fiecare unitate statistica daca distributia ar fi omogena;

3. c - cele doua variabile se refera la aceeasi colectivitate;

4. e - pentru o serie de distributie de frecvente, media calculata pe baza frecventelor relative este egala cu media aritmetica determinata pe baza frecventelor

5. a - prezinta valoarea din mijlocul unei serii de date in care observatiile au fost ordonate crescator sau descrescator;

6. c - quartila unu;

7. c - quartila trei;

8. c - cuartila a doua;

9. a - quartila trei;

10. a suma termenilor seriei ramane aceeasi;

11. a - variatia sub influenta factorilor aleatori (variatia reziduala);

12. b - modul;

13. c -M_o = x_i-1 - h_Mo

14. b - distributie de frecvente;

15. d - mediana;

16. a tendintei centrale si gradului de asimetrie;

17. b patru parti egale;

18. b intervalul modal;

19. a - sintetiza datele;

20. b - A_s= 3(-Me);

21.a - C_asq= ; unde: Q₁= M_e-Q₁

Q₂=Q₃-M_e

22. a - β₂=_;

23. a - β₂ = 3, ∆ = 0;

24. b - β₂ > 3, ∆ >0;

25. c - β₂ < 3, ∆< 0;

26. b - ;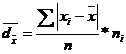

27. c. boltirii.

28. a - limitele inferioare si superioare ale intervalelor extreme;

6. Raspunsuri corecte.

1. Raspuns. Se foloseste formula mediei aritmetice pentru o serie simpla.

= = = 1117,28 milioane lei.

Interpretare: Valoarea medie a volumului vanzarilor zilnice este de 1117,28 milioane lei.

2. * Elementele de calcul sunt prezentate in tabelul urmator:

X_i= lim_inf + sau x_i = =

Rsp. Nivelul mediu al vanzarilor zilnice se afla calculand media aritmetica care in cazul unei serii grupate pe intervale de variatie se calculeaza dupa relatia:

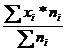= = = = 11,47 milioane lei.

= 11,47 mil lei valoarea medie a volumului vanzarilor este de 11,47 mil lei.

3. Raspuns: Mo=

D₁=n_mo-n_mo-1=12-10=2 ; D₂=n_mo-n_mo+1 =12-6=6

4. Raspuns. Pentru o serie simpla cu numar impar de termeni, ordonati in sens crescator, mediana se afla depistand termenul central al seriei, in dreptul locului medianei.

Loc_me= ==3 → Me = 9 milioane lei.

Locul medianei este al 3-lea termen al sirului (5,7,9,14,20), deci M_e=9 milioane.

5. Raspuns. Pentru o serie simpla cu numar par de termini, ordonati in sens crescator, mediana consta in calcului mediei aritmetice simple a celor 2 termeni centrali ai seriei.

Sirul de date ordonate crescator este: 10,15, 20, 22, 35, 40.

Me = = 21 milioane lei.

6. Raspuns. Loc_me=

Prima frecventa cumulata mai mare decat locul medianei ne indica valoarea medianei. In cazul nostru, prima frecventa cumulata mai mare decat 17,5 este 27, iar intervalul mdian va fi 2.

(n_i=27) ≥ (Loc_me = 17,5)

7. Raspuns. Se calculeaza locul medianei.

Loc_me=

Me= x_infme+h_me

Me=60+30

Interpretare: Jumatate din numarul total al muncitorilor au consumat pentru realizarea produsului A pana la 72,75 minute, iar jumatate au consumat peste 72,75 minute

8. Raspuns: Q₁=lim_infQ1+h_q1*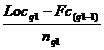

Loc_Q1===50,25

Se calculeaza frecventa absoluta cumulata crescator. Prima frecventa mai mare ca valoare deccat locul cuartilei 1 ne indica intervalul quartilic 1.

Lim_inf=30, deoarece intervalul Q₁ este

h_Q1=60 30 = 30

Fc(_Q1-1) = 25

n_Q1= 50

Q₁= 30+30*=30+30*0,50 =30+15= 45

Interpretare: 25% din numarul total al muncitorilor consuma cel mult 45 de minute pentru realizarea unei piese.

9. Raspuns. Loc_q3=

Q₃= x_infQ3+h_Q3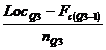

Se calculeaza frecventa absoluta cumulata crescator. Prima frecventa mai mare ca valoarea deccat locul quartilei 3 ne indica intervalul quartilic 3.

Interpretare: 75% din numarul total al muncitorilor consuma cel mult 100,75 minute pentru realizarea unei piese.

10. Raspuns. Media = 181,75

Abaterea medie liniara = 2,42 mil lei → pe ansamblul firmelor se realizeaza o cifra de afaceri lunara care variaza in medie fata de nivelul mediu, cu 2,42 mil lei, in sens pozitiv sau negat

1.se calculeaza centrul de interval

2.se calculeaza media

3. se calculeaza abaterea medie liniara.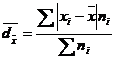

11. Raspuns. C_asq= = =

= = 0,016

12. Raspuns. Coeficientul de asimetrie Yule se calculeaza dupa relatia:

C_asq= = = -3

Q₁= M_e-Q1=130-150= -20

Q₂=Q₃-M_e= 140-130= 10

Interpretare: Valoarea obtinuta, C_asq= -3<0 arata ca distributia considerata este asimetrica la stanga.

13. Raspuns. Coeficientul de boltire se calculeaza dupa relatia:

β_{2= =} = 4

m₄= 40.000

m₂² = (100)² = 10.000

14. Raspuns. β₂= ₌ = = 2,045 si arata o distributie usor platicurtica deoarece

β₂ < 3 ( curba este mai turtita decat cea normala).

Daca β₂ = 3 → simetrie simetrica, iar daca β₂ > 3 atunci aveam o distributie leptocurtica deoarece curba era mai ascutita decat cea normala.

15. Raspuns. Coeficientul empiric de asimetrie Pearson se determina dupa relatia:

C_as= 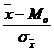== 0, 417.

Interpretare: Valoarea obtinuta, C_as = 0,417 >0, arata ca distributia considerata este puternic asimetrica la dreapta.( curbele sunt alungite spre dreapta).

16. Raspuns: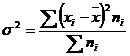

1. Se calculeaza centrul de interval.

2. Se calculeaza media.

=

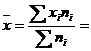
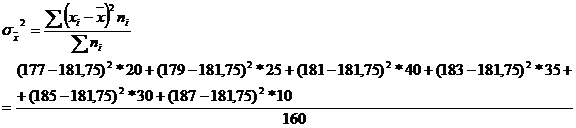
17. Raspuns: (coeficientul de boltire)

Interpretare: Pentru < 0, distributia considerata este platicurtica.