Analiza asimetriei repartitiilor empirice

Analiza asimetriei repartitiilor empirice

O analiza statistica completa a seriilor de repartitie cuprinde, pe langa caracterizarea tendintei centrale in cadrul seriilor, a imprastierii valorilor individuale fata de tendinta centrala, si o analiza a formei in care se repartizeaza frecventele in functie de valorile individuale inregistrate. Forma repartitiilor se analizeaza in primul rand cu ajutorul metodei grafice: histogramei, poligonul frecventei si a curbei cumulative a frecventelor.

Intr-o serie de repartitie perfect simetrica, frecventele valorilor individuale sunt egal repartizate de o parte si de alta a valorilor centrale, iar cele trei valori ale tendintei centrale, respectiv valoarea medie, mediana si modala sunt egale.

In functie de pozitia si valorile pe care le au cei trei indicatori ai tendintei centrale, se pot intalni:

serii simetrice;

serii usor asimetrice;

serii cu tendinta pronuntata de asimetrie.

a). Caracterizarea si masurarea asimetriei se poate face cu ajutorul coeficientului de asimetrie, propus de K.Pearson, calculat cu formula:

Acest coeficient ia valori in intervalul: C_as I

Intr-o serie perfect simetrica C_as =0, deoarece x =M_e=M_0.

Daca x >M₀; atunci C_as I asimetrie pozitiva.

Daca x <M₀; atunci C_asI asimetrie negativa.

f_i    f_i f_i

f_max

x_i Mo Me x x_i x Me

x =Me=Mo

x>Mo    x< Mo

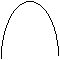
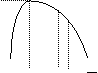
a.serie perfect simetrica    b. asimetrie pozitiva c.asimetrie

negativa

Fig. 3.1. Formele repartitiilor empirice ale unei serii de distributie

b). Un alt procedeu de calcul al coeficientului de asimetrie, propus de K.Pearson, are in vedere mediana si se calculeaza raportand abaterea mediei de la mediana luata de trei ori, la abaterea medie patratica, dupa formula:

unde: C'_as I

Aceasta formula se foloseste pentru seriile usor asimetrice, in care pentru un numar mare de cazuri individuale se verifica relatia :

M₀= x - 3 x - M_e

In serie asimetrica x ¹M_e¹M₀, iar forma unor astefl de serii este "j", "i" sau "u".

Alti coeficienti de asimetrie se pot determina cu ajutorul cuartilelor si decilelor, astfel:

c). coeficientul intercuartilic Yule (c_asy) urmareste evidentierea pozitiei cuartilelor fata de mediana, calculandu-se pe baza formulei:

unde: C_asy I

Daca C_asy =0 serie simetrica.

Daca Q₃ - M_e>M_e - Q₁ C_asyI serie cu asimetrie pozitiva.

Daca Q₃ - M_e<M_e - Q₁ C_asyI serie cu asimetrie negativa.

d). Coeficientul de asimetrie interdecilic a lui Bowley (C_asB) se bazeaza pe relatia dintre decile si mediana, determinandu-se dupa formula:

unde: C_asB I

Cu cat valoarea coeficientului este mai apropiata de zero, cu atat repartitia este mai simetrica, iar cu cat coeficientul este mai apropiat de 1, cu atat seria este mai asimetrica.

Gradul si tendinta de asimetrie se pot caracteriza cu ajutorul indicatorului denumit densitatea de repartitie a frecventelor, util in special in cazul seriilor de repartitie pe intervale mari sau neegale.

Acest indicator se calculeaza raportand fiecare frecventa absoluta sau relativa, la lungimea intervalului respectiv. Daca se utilizeaza frecventele absolute, obtinem densitatea absoluta a frecventelor (d_a), iar daca se utilizeaza frecventele relative, atunci rezulta densitatea relativa a frecventelor (d_r), astfel:

Unde: f_i - frecventa absoluta a intervalului i;

h_i - marimea intervalului i;

f_i^* - frecventa relativa a intervalului i.

Daca valorile acestor indicatori au tendinta de crestere catre valoarea centrala a caracteristicii, inseamna ca seria de distributie are tendinta de normalitate.