Indicatorii variatiei

Indicatorii variatiei

Media sintetizeaza intr-o singura expresie numerica ceea ce este esential si tipic la nivelul de dezvoltare al unei caracteristici. Ea nu poate evidentia - insa - diversitatea valorilor caracteristicii respective si nu ofera nici o informatie privind omogenitatea sau eterogenitatea seriei respective.

Exista situatii in practica in care pentru serii statistice diferite, media este aceeasi.

Aplicatie

Intr-o firma activitatea este derulata de 3 echipe, fiecare de cate 5 angajati, care in luna septembrie 2006 au inregistrat urmatoarele salarii brute (in u.m.):

Echipa A: 600; 700, 800; 900; 1000

Echipa B: 200; 700; 900; 1000; 1200

Echipa C: 800; 800; 800; 800; 800

Daca se calculeaza salariul mediu realizat de fiecare echipa in parte se obtin rezultatele:

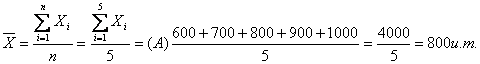
Se constata ca, desi cele 3 serii de date (echipe) sunt complet diferite din punct de vedere al valorilor individuale, salariile medii sunt identice (800u.m.).

In consecinta, pentru efectuarea unei analize corecte si complete se impune apelarea la indicatorii variatiei care permit, printre altele:

caracterizarea omogenitatii / eterogenitatii colectivitatii statistice;

caracterizarea reprezentativitatii mediei.

Indicatorii simpli ai variatiei

A.     Amplitudinea variatiei calculata sub 2 forme:

amplitudinea absoluta (Aa), ca diferenta intre valoarea maxima (X_max) si valoarea minima (X_min) a caracteristicii; se exprima in aceeasi unitate de masura ca si caracteristica studiata.

amplitudinea relativa (A_r), ca raport procentual intre amplitudinea absoluta a variatiei si nivelul mediu al caracteristicii (); se exprima in procente, motiv pentru care permite compararea variatiei mai multor caracteristici ale aceleiasi colectivitati.

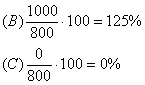
In mod evident:

cu cat amplitudinea (absoluta si relativa) este mai mare, cu atat colectivitatea este mai eterogena;

cu cat amplitudinea (absoluta si relativa) este mai mica, cu atat colectivitatea este mai omogena.

Principala deficienta a amplitudinii variatiei o constituie faptul ca depinde numai de valorile extreme ale caracteristicii, fara a furniza nici o informatie referitoare la "imprastierea" celorlalte valori ale seriei.

Totusi, amplitudinea variatiei este un indicator des utilizat in practica, in special atunci cand este calculat dupa eliminarea asa-ziselor " cazuri aberante ". O astfel de situatie apare in cazul echipei B la care un angajat figureaza cu un salariu brut lunar de 200 u.m., mult sub nivelul celorlalti angajati.

Deficienta mentionata anterior poate fi partial ameliorata prin calculul abaterilor individuale fata de medie.

B.     Abaterile individuale fata de medie calculate, la randul lor, sub 2 forme:

abaterile individuale absolute (), ca diferenta intre fiecare valoare inregistrata si nivelul mediu:

abaterile individuale relative , ca raport procentual intre abaterea individuala absoluta si nivelul mediu al caracteristicii

Echipa A

Echipa B

Echipa C

Cum numarul abaterilor individuale este foarte mare, de cele mai multe ori, in analiza se utilizeaza abaterea maxima pozitiva si abaterea maxima negativa.

In exemplul anterior, ambele extreme se intalnesc la echipa B:

ca efect al faptului ca aceasta echipa inregistreaza cea mai mare eterogenitate din punct de vedere al distributiei salariilor.

Indicatorii simpli ai variatiei nu pot cuantifica intr-o singura expresie numerica intreaga variatie a unei caracteristici, motiv pentru care se apeleaza la indicatorii sintetici ai variatiei.

Indicatorii sintetici ai variatiei cuantifica intr-o singura expresie numerica intreaga variatie a unei caracteristici, oferind o imagine sintetica a imprastierii (dispersarii) valorilor caracteristicii, tinand cont de toti termenii seriei.

Principalii indicatori sintetici ai variatiei sunt:

A.       Abaterea medie patratica sau abaterea standard () se calculeaza ca o medie patratica (simpla sau ponderata) a abaterilor individuale ale termenilor seriei de la media lor.

In mod normal, cuantificarea tuturor abaterilor individuale am fi tentati sa o calculam prin insumarea acestora si determinarea mediei aritmetice:

De la proprietatile mediei aritmetice se cunoaste ca suma abaterilor individuale este 0, urmare a faptului ca abaterile pozitive sunt compensate de abaterile negative.

In consecinta, abaterea standard nu se poate calcula pe baza formulei mediei aritmetice, apelandu-se in acest scop la media geometrica.

Prin media geometrica, termenii seriei sunt mai intai ridicati la patrat (astfel incat termenii negativi devin pozitivi), iar in continuare pentru a contracara efectele operatiunii anterioare se aplica functia inversa ridicarii la patrat, adica extragerea radacinii patratice (radicalul).

Ca urmare, relatia de calcul pentru abaterea medie patratica este urmatoarea:

pentru o serie simpla

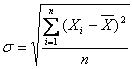
pentru o serie cu distributie de frecvente

In exemplul anterior se calculeaza abaterea medie patratica pentru fiecare echipa in parte.

Echipa A

Echipa B

Echipa C

Rezultatele obtinute reflecta faptul ca:

echipa B este cea mai eterogena din punct de vedere al salariatilor, aceasta avand o variatie medie de 340,6u. m., in plus sau in minus fata de salariul mediu (880 u.m.);

echipa A este mai omogena, variatia medie fiind de 141,4 u.m.;

echipa C este perfect omogena.

Abaterea medie patratica prezinta urmatoarele caracteristici:

se exprima in aceeasi unitate de masura ca si caracteristica respectiva, avand o semnificatie clara si usor de inteles;

nu poate fi utilizata pentru a se face aprecieri comparative referitoare la variatia unor caracteristici diferite, chiar daca aceasta vizeaza una si aceeasi colectivitate.

Pentru a contracara aceasta ultima deficienta se foloseste coeficientul de variatie.

B.        Coeficientul de variatie se calculeaza ca raport procentual intre abaterea medie patratica si nivelul mediu al seriei .

Coeficientul de variatie este considerat cel mai complet indicator al cuantificarii imprastierii valorilor unei anumite caracteristici, oferind o imagine convingatoare asupra omogenitatii sau eterogenitatii colectivitatii statistice si reprezentand un veritabil test de verificare a reprezentativitatii mediei.

Coeficientul de variatie poate lua numai valori pozitive, situate intr-un interval limitat:

cu cat are o valoare mai mica cu atat seria este mai omogena si deci media mai reprezentativa;

se apreciaza ca pentru v>30%, media nu este reprezentativa, colectivitatea este neomogena si trebuie separata in subcolectivitati omogene, urmand ca acestea sa fie analizate distinct.

Pentru aplicatia anterioara rezultatele sunt urmatoarele:

<

>

Concluzii finale:

echipa A prezinta un grad de omogenitate acceptabil, iar salariul mediu poate fi apreciat ca reprezentativ;

echipa B este neomogena (v>30%), media este nereprezentativa, iar analiza trebuie realizata pe subcolectivitati (de exemplu, eliminarea din calcul a variantei "aberante" in care salariul este de 200 u.m.);

echipa C este perfect omogena.

C.       Dispersia sau varianta se calculeaza ca medie aritmetica (simpla sau ponderata) a patratelor abaterilor termenilor fata de media lor. Cu alte cuvinte, dispersia este abaterea standard ridicata la patrat.

pentru o serie simpla

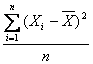
pentru o serie cu distributie de frecvente

Ca urmare, calcularea abaterii medii patratice implica calcularea dispersiei:

In practica, pentru simplificarea calculelor se poate apela la urmatoarele relatii:

pentru o serie simpla

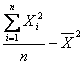
pentru o serie cu distributie de frecvente

Valoarea dispersiei nu are un continut concret, asa cum de exemplu se intampla in cazul abaterii medii patratice. Cu toate acestea, dispersia se utilizeaza frecvent in statistica in analize ulteriore privind regula de adunare a dispersiilor si analiza dispersionala.