Subiecte rezolvate statistica

1. Fenomenele de masa. Def si particularitati

Statistica, indiferent de acceptiunea sa, se ocupa cu studiul cantitativ al fenomenelor de masa in scopul evidentierii trasaturilor cantitative din formele lor de manifestate (sau evidentierii legilor statistice sub care se manifesta aceste fenomene). Aceasta inseamna ca statistica are ca functie principala realizarea procesului de cunoastere si fundamentare a deciziilor de actiune.

Exemplu de fenomene de masa: h, g, culoarea ochilor, a parului, dobanda practicata de banci, opinia consumatorilor asupra unui produs, obtiunea electoratului pentru un candidat. Fenomenele de masa, prin definitie, sunt fenomene variabile. Prin studiul cantitativ-numeric al fenomenomenelor de masa, identificam trasaturile calitative ale manifestarii fenomenului, sau identificam legea statistica sub care se manifesta fenomenul in populatia investigata. Aceasta lege se manifesta ca tendinta la nivelul ansamblului, ea nu poate fi verificata in fiecare caz in parte.

2. Notiuni fundamentale ale statisticii

In studiul cantitativ al fenomelor de masa, statistica utilizeaza un numar mare de concepte, unele dintre acestea sunt utilizate in toate etapele cercetarii statistice indiferent de natura fenomenului sudiat si formeaza vocabularul de baza al statisticii, altele sunt specifice anumitor etape, anumitor metode, fenomene de masa. Dintre notiunile vocabularului, mentionam:.

* Colectivitatea sau populatia statistica reprezinta un ansamblu de unitati de aceeasi natura, de la care se inregistreaza date statistice. Populatiile statistice pot fi: - statice , - atunci cand timpul este constant iar spatiul si forma de organizare sunt variabile, - dinamice, – atunci cand timpul este variabil iar spatiul si forma de organizare sunt constante. Numarul de unitati ce compun o unitate statistica se noteaza cu N si reprezinta volumul populatiei sau colectivitatii statistice.

* Esantionul, proba sau mostra reprezinta o subpopulatie extrasa printr-un procedeu aleator, dirijat sau mixt. Numarul de unitati cuprinse in esantion reprezinta volumul esantionului si se noteaza cu n.

* Unitatile statistice sunt elemente componente ale populatiilor sau colectivitatilor,sunt purtatoare de date statistice, sunt purtatoare de valori individuale ale variabilelor studiate, urmarite. Ca si populatiile, unitatile pot fi statice sau dinamice, pot fi simple (studentul, persoana, unitatea economica) si complexe (grupa de stdenti, familia, departamentele unitatilor economice).

*Caracteristica nu reprezinta altceva decat trasatura, proprietatea, insusirea comuna a unitatilor investigate. Din aceasta cauza, caracteristicile statistice se mai numesc si variabile statistice, iar valorile acestor variabile sunt expresii ale formelor de manifestare ale caracteristicii. Variabilele statistice, in functie de natura lor pot fi: de timp, de spatiu sau teritoriale, si atributive. Valorile variabilelor de timp desemneaza apartenenta unitatilor la un moment sau interval de timp. Valorile variabilelor teritoriale desemneaza apartenenta unitatilor la un anumit teritoriu.

Variabilele atributive se caracterizeaza prin faptul ca valorile acestora sunt exprimate prin atribute. In functie de natura acestor atribute exista:

- variabile numerice (cantitative), exprimate numeric,

- variabile nenumerice (calitative) exprimate prin cuvinte.

Dupa repetabilitatea valorilor individuale exista:

variabile alternative (prezinta doar doua variante)

- nealternative, care prezinta mai mult de doua variante.

Dupa natura variatiei,caracteristicile numerice pot fi :

- variabile cu variatie continua (iau valori intr-un interval)

- variabile cu variatie discreta, discontinua. Acestea prezinta valori doar numere intregi.

*frecventa de aparitie. Frecventa absoluta (ni) arata de cate ori se repeta valoarea variantei caracteristicii in populatia investigata sau exprima numarul de unitati la care s-a inregistrat aceeasi valoare individuala. Intr-o populatie statistica urmarim variabila X , o varianta a acestei variabile este Xi. In afara frecventei absolute, valorile variabilelor investigate pot avea si frecvente relative exprimate in coeficienti sau procente. Relatia de calcul a acestora este:

n₁ n₁

f_i= —―exprimata in coeficienti; fi= —― x 100exprimata in procente;

k                                                    k

∑_ni ∑_ni

^{i = 1 i = 1}

k = numarul de variante distincte ale variabilei sau caracteristicii urmarite

6

∑ _ni = n₁₊n₂₊n₃₊n₄₊n₅₊n₆

Suma frecventei relative exprimate in coeficienti este egala cu 1.

Suma frecventei relative exprimate in % =100.

* Data statistica Spre deosebire de numerele abstracte cu care opereaza matematica, se caracterizeaza prin expresie numerica dar si prin identificatori de continut, timp, spatiu si forma de organizare. Ex: 4. 09 lei/euro, cursul leu/euro la casa de schimb valutar X in data de 15. 03. 2010,filiala Braila,a firmei Y.

Din compararea datelor statistice prin raport sau diferenta, prin agregarea (insumarea) datelor, se obtin indicatori statistici Prelucrand prin diverse operatii variabilele indicatorilor statistici si interpretand rezultatele se obtine informatia statistica.

3. Metode de culegere a datelor. Programul de organiz a unei observari

Sistemul informational statistic cuprinde multitudinea operatiilor necesare efectuarii cercetarii statistice. In succesiunea lor, etapele cerctarii statistice sunt:

- culegerea sau inregistrarea datelor - sistematizarea, clasificarea si prezentarea datelor culese

- prelucrarea datelor sistematizate- interpretarea rezultatelor prelucrarii - formularea concluziilor

- arhivarea sau stocarea datelor - baze de date sau banci de date

1. Prima etapa a cercetarii statistice este culegerea datelor. Aceasta etapa este deosebit de importanta deoarece de calitatea datelor inregistrate depinde calitatea rezultatelor prelucrarii acestora, depinde cunoasterea si implicit calitatea deciziilor adoptate.

Observarea este directa, indirecta, periodica, permanenta, totala, partiala.

Metodele de culegere se clasifica dupa diverse criterii, astfel:

- in functie de modalitatea de inregistrare

- metode de culegere permanete – datele sunt inregistrate pe masura producerii fenomenului.

- metode de inregistrare periodice. in acest caz intervin: recensamantul, anchetele

- dupa numarul de unitati de la care se culeg datele

- observari totale- cand se inregistreaza date de la toate unitatile colectivitatii-(recensamantul)

- observari partiale (cand se culeg date doar de la o parte a colectivitatii statistice)

- dupa modalitatea de inregistrare a datelor

- observari directe- cand datele sunt culese de catre cercetatori de la unitatile statistice nemijlocit

- obs. indirecte-se realizeaza atunci cand datele ref la o unitate stat sunt culese din alte surse.

Aplicarea sau utilizarea unei metode de culegere a datelor nu poate fi facuta la intamplare, ci pe baza unui program. Indiferent de metoda, programul de culegere(inregistrare) a datelor trebuie sa cuprinda anumite elemente, dintre care mentionam:

-trebuie precizat scopul observarii. Acest scop poate sau nu, sa coincida cu scopul cercetarii. Acest scop trebuie formulat in termeni precisi pentru a fi inteles in mod unitar de cei care culeg datele, pentru a nu afecta calitatea datelor.

-trebuie precizata populatia statistica supusa observarii. In acest context, populatia trebuie delimitata in timp, spatiu si dpdv organizatoric, dupa diferite criterii.

-trebuie precizate unitatile statistice de la care se culeg datele.

-trebuie precizate variabilele sau caracteristicile despre care se culeg date de la unitatile populatiei. Aceste variabile trebuie precizate fie intr-o lista, fie intr-un chestionar.

-timpul- trebuie privit sub dublu aspect, ca perioada sau interval de timp in care se culeg datele, sau ca moment critic la car se refera datele(moment de referinta). Intervalul de timp in care se realizeaza inreg. datelor trebuie sa fie astfel ales incat pop. statistica sa fie maxima.

-locul observarii - se precizeaza pentru a identifica mai usor unitatile de la care se culeg datele. In acest scop sunt elaborate planuri, carti, machete.

-masuri organizatorice - se refera la elaborarea, tiparirea si distribuirea chestionarelor, recrutarea si pregatirea personalului care culege date. Intre datele culese si cele existente in realitate pot exista diferente numite si erori de observare. Aceste erori pot fi:

- obiective, determinate de factori aleatori, care nu influenteaza rezultatele prelucrarii,

-sistematice, greseli provocate de factori subiectivi (neintelegerea scopuluui cercetarii, erori datorate persoanei care culege datele). Aceste erori sistematice influenteaza rezultatele cercetarii. Datorita cauzelor obiective spunem ca erorile de observare nu pot fi eliminate, ci doar limitate.

Prelucrarea datelor. Prelucrarea primara a datelor

Pentru a exprima esenta din manifestarea fenomenului, pentru a identifica legea statistica, este necesar ca datele statistice controlate sa intre intr-un proces de prelucrare:

1. Sistematizarea datelor culese

2. Clasificarea si gruparea datelor culese

3. Prezentarea datelor sistematizate in tabele, serii si grafice.

4. Calcului,analiza si reprezentarea grafica a indicatorilor primari, relativi.

4. Scale de masurare folosite in statistica

Variabilele atributive, in functie de natura lor, prezinta valori pe diferite scale. Principalele scale de masura sunt:- scala nominala- scala ordinala- scala de interval- scala de raport

Variabilele exprimate prin cuvinte prezinta valori pe scala nominala. Ex: variabila profesie pe aceasta scala prezinta urmatoarele valori: turnator, lacatus, matriter etc. Valorile de pe aceasta scala nu se supun operatiilor algebrice. Aceasta inseamna ca utilizand aceste valori nu se pot obtine indicatori sintetici. Se poate doar stabili frecventa fiecarei valori de pe aceasta scala (cati lacatusi, cati turnatori, cati matriteri).

Variabilele atributive prezinta valori pe o scala ordinala, valorile pe o astfel de scala prezinta ordine

Valorile de pe aceasta scala nu se supun operatiilor algebrice, in schimb pot avea semnificatii dife-

rentele dintre doua sau mai multe valori consecutive, succesive.

Scalele de interval si de raport se deosebesc de precedentele prin faptul ca permit efectuarea de operatii algebrice si implicit calculul indicatorilor sintetici. Diferenta dintre scala de interval si scala de raport este data de semnificatia valorii 0 (zero). Pe scala de interval, valoarea 0 are o semnificatie concreta, aceasta presupune absenta variabilei sau caracteristicii. Pe scala de raport valoarea 0 inseamna lipsa caracteristicii.

5. Indicatorii relativi:tipuri,mod de calcul,reprez. grafica

In cazul in care compararea datelor se realizeaza prin raportare se obtin indicatorii relativi. Indicatorii relativi, cu o singura exceptie se exprima in coeficienti sau in procente. In functie de datele comparate exista urmatoarele grupe de indicatori relativi:

- indicatori relativi de structura;

- indicatori relativi de dinamica;

- indicatori relativi ai planului sau programului;

- indicatori relativi de coordonare;

- indicatori relativi de intensitate.

Indicatorii relativi de structura (ponderi, greutati specifice)

Acestia exprima ponderea unei parti dintr-un intreg (cat la suta reprezinta o parte in intreg). Se calculeaza in general prin relatia: g_i^x = x_i /∑_xi exprimata in coeficienti, sau daca inmultim raportul cu 100 atunci greutatea specifica este exprimata in procente. Valorile acestor indicatori sunt cuprinse in intervalul 0-1 sau 0-100. Suma indicatorilor relativi de structura este egala cu 1 sau 100. Acesti indicatori se reprezinta grafic prin diagrama de structura realizata cu ajutorul dreptunghiului, patratului, cercului.

Indicatorii relativi de dinamica (indicii de dinamica) se determina comparandu-se prin raportare, valori ale aceleiasi variabile inregistrate in unitati de timp diferite. Relatia de calcul este:

Acest indice poate fi:

- mai mare ca 1 sau 100 cand exprima o crestere a valorilor variabilei x ,

- egal cu 1 sau 100 cand exprima o stagnare,- mai mic ca 1 sau 100 cand exprima o scadere.

Acest indice arata de cate ori sau de cat la % s-a modificat valoarea variabilei x in per. t fata de t’

In functie de baza de comparatie t’ exista indici de dinamica cu baza fixa si indici de dinamica cu baza mobila. Un indice de dinamica cu baza fixa arata de cate ori sau de cat la % s-a modificat valoarea variabilei x din fiecare perioada fata de aceiasi perioada baza de comparatie. Intr-o serie de timp de lungime relativ mica (sub 10 termeni) se ia ca baza de comparatie primul termen din serie. Indicele de dinamica cu baza fixa arata amploarea evolutiei in timp a unui fenomen. Regularitatea in timp a fenomenului poate fi determinata calculandu-se indici de dinamica cu baza mobila. Un indice de dinamica cu baza mobila arata de cate ori s-a modificat valoarea inregistrata de variabila x in perioada t fata de perioada precedenta. Relatia este:

x_{t ────}

I^x_t/t’ = ── , ( ۷ )t = 1,T

x_t’

Indicii de dinamica cu baza fixa sau cu baza mobila se reprezinta grafic cu diagrama prin benzi si cu diagrama prin coloane,sau cu cronograma.

Indicatorii relativi ai planului sau ai programului

Notam cu:

x₀ - valoarea inregistrata de variabila x intr-o perioada anterioara

x_p - nivelul planificat al variabilei x pentru perioada curenta

x₁ - nivelul variabilei x relizat in perioada curenta

Comparand cele trei valori prin raportare se obtin indicatorii planului sau programului, astfel:

numit gradul sarcinii de plan sau de program.

Arata de cate ori s-a programat mai mult sau mai putin fata de cat s-a relizat intr-o perioada anterioara. Acest indice poate fi:

- mai mare ca 1 sau 100, cand s-a planificat mai mult decat s-a relizat in perioada precedenta,

- egal cu 1 sau 100 cand s-a planificat cat s-a realizat anterior,

- mai mic ca 1 sau 100 cand s-a programat mai putin.

Indicele sau gradul indeplinirii planului sau programului, arata de cate ori sau de cat la suta s-a realizat in perioada curenta mai mult sau mai putin fata decat s-a programat sau planificat

Indicatorii relativi de intensitate

Se determina ca raport intre doua variabile diferite intre care exista o legatura de cauzalitate

Exemplu: productivitatea muncii , pretul V = valoarea, C= cantitatea.

Indicatorii relativi de intensitate se exprima in unitati de masura concrete. Se reprezinta grafic printr-un dreptunghi . O atentie deosebita trebuie acordata in determinarea acestor indicatori, la un nivel de agregare superior. _

__ ∑_Q1∑_{Wi ;Ti _}

W = ─── = ──── = ∑_{W ;} g^T_i Ti = variabila

∑_T1 ∑ _Ti

Indicatorii relativi de coordonare – se determina raportandu-se valori ale aceleasi variabile inregistrate in populatii sau unitati teritoriale diferite:

6. Indicatorii sintetici ai variatiei (imprastierii)

Acesti indicatori se caracterizeaza prin faptul ca exprima variatia (imprastierea) valorilor individuale inregistrate fata de tendinta centrala intr-o singura expresie numerica. In categoria indicatorilor sintetici ai variatiei incadram:

- abaterea medie liniara;

- dispersia;

- abaterea medie patratica;

- coeficientul de variatie sau omogenitate.

Abaterea medie liniara exprima cu cate unitati de masura se abat in medie valorile individuale de la tendinta centrala. Acest indicator se determina cu o medie aritmetica simpla sau ponderata a abaterilor valorilor individuale luate in modul. Daca tendinta centrala o caracterizam cu media aritmetica, relatiile de calcul sunt:

- pentru serii simple: 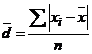(_{in modul)}

- pentru serii de frecvente absolute: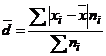

- pentru serii de frecvente relative exprimate in coeficienti:

- pentru serii de frecvente relative exprimate in % :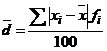

Observatii:

- acest indicator se exprima in unitatea de masura a variabilei numerice studiate;

- din calcul se observa ca acest indicator ia valori in intervalul [0,∞] . Cu cat valorile sunt mai apropiate de 0 cu atat seria este mai omogena si media mai reprezentativa; cu cat valorile sunt mai mari, seria este eterogena si media mai putin reprezentativa.

Dispersia exprima gradul de imprastiere al valorilor individuale fata de tendinta centrala. Acest indicator se determina ca o medie aritmetica simpla sau ponderata a patratelor abaterilor valorilor individuale de la media lor. Relatii de calcul:

σ² = 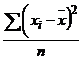pentru serii simple,

σ²= 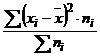pentru serii de frecvente absolute.

Daca frecventele sunt relative (f_i) in relatia precedenta, acestea inlocuiesc pe cele absolute (n_i)

Observatii:

- dispesia nu are unitate de masura cu continut economic real. Acest indicator ia valori in intervalul[0, ∞] cu cat valorile sunt mai mici, cu atat mai mica este dispersia, seria este mai omogena iar media mai reprezentativa. In mod conventional, dispersia poate fi determinata si pentru variabila alternativa de tip DA,NU.

σ²=

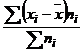
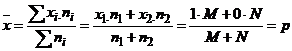
σ²⁼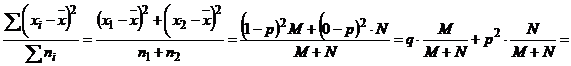

=

Abaterea medie patratica(abaterea standard) arata cu cate unitati de masura se abat in medie valorile individuale inregistrate de la tendinta centrala. Acest indicator se determina ca o medie patratica a valorilor individuale. Relatia de calcul este:

Acest indicator are unitate de masura cu continut real. Acest indicator este cel mai utilizat pentru caracterizarea imprastierii sau omogenitatii, pentru ca este parametru al legilor teoriei de repartitie (ex: al repartitiei normale) Acest indicator se exprima in unitatea de masura a variabilei; ia valori in intervalul [0,∞].

Indicatorii sintetici prezentati au urmatorul neajuns:

- ei iau valori in intervalul [0,∞] si nu intr-un interval concret. Din aceasta cauza, cu cat valoarea indicatorilor sintetici este mai mica, omogenitatea este mai mare, cu atat reprezentativitatea mediei este mai mare. Neajunsul prezentat este eliminat prin determinarea coeficientului de variatie (omogenitate). Acest coeficient se calculeaza ca raport procentual intre abaterea medie liniara sau abaterea medie patratica si nivelul mediu.

sau

Indiferent cum se calculeaza, acest indicator ia valori intervalul (0-100). Un coeficient care se apropie de 0 arata lipsa variatiei,colectivitatea fiind alcatuita din termeni foarte omogeni. Daca CV = 0, termenii seriei sunt egali intre ei. Din statistica experimentala s-a preluat aprecierea urmatoare:

- daca CV este pana la 35 % se considera ca intensitatea variatiei este redusa, colectivitatea este omogena si in consecinta media este reprezentativa. Cu cat se depaseste pragul de 35% cu atat intensitatea variatiei creste iar colectivitatea este mai eterogena, in aceste conditii media tinde sa devina o marime reprezentativa. Daca CV>50% , varianta caracteristicii este foarte mare, colectivitatea nu este omogena, media nu este reprezentativa;este necesara regruparea datelor. Dupa caracterizarea variatiei fata de tendinta centrala, este necesar sa analizam forma repartitiei,respectiv asimetria repartitiei.

7. Indicatorii medii de pozitie(ai tendintei centrale)

In categoria indicatorilor tendintei centrale se cuprind;

- indicatori medii

- mediile de pozitie (de structura sau localizare)

Indicatori medii

Media exprima tendinta centrala, intrucat intr-o singura expresie numerica sintetizeaza ceea ce este comun, stabil si permanent in datele din care aceasta se calculeaza. Media are un caracter abstract deoarece poate sau nu poate sa coincida cu nici o valoare individuala inregistrata. Media se determina luandu-se in considerare toate datele inregistrate, ceea ce inseamna ca nivelul sau este influentat de valorile extreme. Mediile se determina numai pentru variabilele numerice indiferent daca sunt cu variatie discreta sau continua. Media aritmetica

Media aritmetica este acea valoare a variabilei care s-ar fi inregistrat daca la nivelul fiecarei unitati de observare ar fi actionatat aceeasi factori de influenta cu aceeasi intensitate, in aceeasi directie.

Media aritmetica este acea valoare a variabilei care daca ar substitui fiecare valoare individuala inregistrata, suma acestora nu s-ar modifica. Prin urmare, media aritmetica se recomanda sa se utilizeze atunci cand intre date este obiectiva insumarea acestora.

∑ x₁

i=1

= ───── ( pentru serii simple )

n

Observatii si proprietati:

- media aritmetica se aplica atunci cand relatia dintre date in mod obiectiv este de insumare, sau cand sirul de date se prezinta sub forma unei progresii aritmetice sau cand fenomenul are o evolutie aproximativ liniara

- nivelul mediei aritmetice se incadreaza intre valoarea cea mai mica si valoarea cea mai mare inregistrata la nivelul colectivitatii analizate. x_min < < x_max

- suma abaterilor valorilor individuale fata de media lor aritmetica = 0 ,zero

- in cazul seriilor de distributie de frecvente se determina media aritmetica ponderata dupa urmatorul rationament:

n

∑ . (x_i -) =0

i=1

r

∑ x_i n_i

i=1

= ──────── pentru serii de frecventa absoluta

r

∑ n_i

r

∑ x_i f_i

i=1

= ──────── pentru serii de frecventa relativa exprimata in procente

100

r

= ∑ x_i f_ipentru serii de frecventa relativa exprimate in coeficienti, unde:

i=1

r reprezinta numarul de variante distincte ale variabilei x

x_i - varianta distincta i inregistrata la n_i unitati

n_i - frecventa absoluta de aparitie a variantei x_i

∑ n_i - volumul colectivitatii generale

n_i

f_i = ─── (frecventa relativa de aparitie a variantei x_i)

∑ n_i

∑ f_i = 1 sau 100 dupa cum frecventele relative sunt exprimate in coeficienti sau procente

In cazul seriilor de distributie pe intervale, in relatiile mediei aritmetice ponderate se iau in calcul mijloacele (centrele) intervalelor, in ipoteza ca in fiecare interval, frecventele se distribuie in mod uniform. Centrul unui interval se determina ca media aritmetica a limitelor intervalului respectiv.

Mediile de pozitie sau de structura

In categoria acestor medii incadram valoarea modala (Mo) si cuantilele.

Valoarea modala se mai numeste valoare dominanta sau valoare cu cea mai mare frecventa de aparitie intalnita la cele mai multe unitati de observare. Aceasta reprezinta valoarea individuala cu cea mai mare frecventa intr-o serie de distributie de frecvente pe variante valoarea modala este varianta careia ii corespunde cea mai mare frecventa absoluta sau relativa.

Ex: 2,5,17,17,5,5,12 5-se repeta de cele mai multe oriMo=5

Intr-o serie de distributie de frecvente pe intervale valoarea modala Mo se det. in urmatoarele etape:

1. se identifica intervalul modal (intervalul caruia ii corespunde frecventa maxima)

2. in intervalul modal se determina valoarea modala cu relatia:

Mo = Xo_MO + h_Mo• unde:

Mo- valoarea modala

X_oMo-limita inferioara a intervalului modal

Δ1- diferenta dintre frecventa intervalului modal si frecventa intervalului precedent

Δ 2- diferenta dintre frecventa intervalului modal si frecventa intervalului urmator

Cuantilele de ordin r – Cr -sunt valori ale variabilei care impart seria ordonata crescator in r parti egale, fiecare parte continand 1/r, din numarul unitatilor de observare ale populatiei. Daca r = 2 ,populatia se imparte in doua parti egale, iar cuantila de ordin 2 se numeste mediana.

Mediana- Me – este acea valoare a variabilei care imparte seria ordonata crescator in doua parti egale, fiecare parte contine 50% din nr. total de unitati de observare. Aceasta inseamna ca 50% din valorile inregistrate < decat mediana si 50% > decat valoarea mediana.

Valoarea mediana se determina astfel:

- in cazul seriilor simple cu nr impar de termeni valoarea mediana este termenul din mijlocul seriei ordonate crescator Ex:2,5,7,9,10 Me = 7

- in cazul seriilor simple cu nr par de termeni existand 2 termeni centrali in mijlocul seriei in mod conventional valoarea mediana se determina ca medie aritmetica a celor doi termeni centrali

Ex:2,5,7,10,100,105 Me = = 8,5

In cazul seriilor de distributie de frecvente pe variante valoarea mediana este varianta corespunzatoare primei frecvente absolute sau relative cumulate crescator care depaseste locul medianei

1. determ locul medianei L_Me = 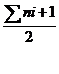; 2. determ frecventei cumulata crescator

n1↑ = n1, n2↑ = n1↑+ n2, n3↑= n2↑+ n3

Identificam mediana ca fiind varianta corespunzatoare primei frecvente absolute sau relative cumulate crescator care depaseste locul medianei

In cazul seriilor de distributie de frecvente pe intervale, valoarea mediana se det. in urmatoarele etape:

1. Se calc L_Me= 2. determ frecventei cumulata crescator 3. se identifica intervalul median -acesta corespunde primei frecvente cumulate crescator care depaseste L_Me 4. Se calc mediana dupa formula Me=x_0Me+h_Me. L_Me-∑_npMe/n_Me unde:

x_0Me-lim inf a interv median; h_Me=marimea interv median; L_Me-locul medianei;∑_npMe/n_Me- suma frecv preced interv median ;

Analiza statistica a variatiei sau imprastierii fata de tendinta centrala

Tendinta centrala reflecta ceea ce este comun, stabil in forma e manifestare a unui fenomen de masa. Pentru ca fenomenele de masa sunt influentate de factori comuni cat si de factori specifici, unitatile de observare ,valorile individuale inregistrate la nivelul fiecarei unitati, se abat intr-un sens sau altul mai mult sau mai putin fata de tendinta centrala. Aceasta imprastiere(variatie) a valorilor individuale fata de tendinta centrala este exprimata cantitativ prin indicatori specifici. Masurand variatia, acesti indicatori exprima omogenitatea valorilor inregistrate, reprezentativitatea val. calculate fata de tendinta centrala (exprimata prin medie sau mediana).

In functie de continutul lor,de modul lor de calcul, indicatorii variatiei sunt clasificati in:

- indicatori simpli

- indicatori sintetici

Indicatorii simpli ai variatiei se caracterizeaza prin faptul ca se determina la nivelul fiecarei unitati de observare sau pe baza unui numar redus de valori inregistrate. In categoria indicatorilor simpli de imprastiere incadram:

- amplitudinea variatiei

- abaterea individuala

Amplitudinea variatiei exprima sub forma absoluta sau relativa abaterea (diferenta) dintre valoarile extrme inregistrate. Sub forma absoluta amplitudinea variatiei se determina cu relatia:

A= x_max-x_{min ,} iar sub forma relativa

Amplitudinea este un indicator slab de imprastiere pentru ca marimea sa este influentata de prezenta valorilor aberante. Din aceasta cauza acest indicator nu reflecta cum sunt imprastiate valorile individuale in intervalul x _min - x_max.

Acest indicator se calculeaza si se utilizeaza , nu atat ca indicator de imprastiere ci ca un indicator intermediar in algoritmul gruparii datelor, ca indicator in metodele statistice de control al calitatii produselor.

Abaterea individuala se determina la nivelul fiecarei unitati simple de observare si se exprima in unitatea de masura a variatiei analizate. Acest indicator exprima cu cu cate unitati de masura se abate fiecare valoare individuala inregistrata de la tendinta centrala, exprimata prin intermediul mediei sau medianei.

- relatia de calcul sub forma absoluta a abaterii individuale

- sub forma relativa

Pe baza acestor valori putem determina sensul abaterilor fata de tendinta centrala . Folosind acest indicator evaluarea sintetica a imprastierii in intreaga populatie statistica nu este posibila pentru ca suma abaterilor individuale de la tendinta centrala este = 0. Intr-o singura expresie numerica imprastierea valorii individuale fata de tendinta centrala in intreaga populatie statistica este exprimata cu ajutorul indicatorilor sintetici de imprastiere (variatie)

8. Caracterizarea statistica a formelor de repartizare a frecventelor

Caracterizarea statistica a asimetriei repartitiei

Analiza asimetriei se realizeaza doar pentru seriile unimodale(cu o singura valoare modala). O serie este asimetrica atunci cand majoritatea valorilor individuale sunt deplasate catre valorile mari sau catre valorile mici. Forma asimetriei o observam suprapunand pe histograma sau poligonul frecventelor, legea normala (clopotul lui Gaus).

Astfel daca ,atunci exista simetrie perfecta.

Daca, atunci exista asimetrie pozitiva sau de stanga.

Daca, exista asimetrie negativa sau de dreapta.

Aprecierea de stanga sau de dreapta provine din observarea pozitiva in care se afla valoarea modala M_o fata de medie () pe axa abciselor, in cazul unei serii de repartitie asimetrica. Amploarea asimetriei o estompam prin intermediul unor coeficienti specifici dintre care precizam:

sauMe – mediana

Acesti coeficienti iau valori in intervalul[-1,+1] . Daca C_as =0, seria este simetrica, cu cat valorile sunt mai apropiate de 0 seria este mai simetrica. Cu cat valorile sunt mai apropiate de [-1, +1] seria este mai asimetrica.

Daca C_as ia valori in intervalul [-1,0] seria prezinta o asimetrie negativa, deplasare pronuntata catre valorile mici.

Daca C_as ia valori in intervalul [0,+1] seria prezinta o asimetrie pozitiva,deplasare pronuntata catre valorile mari.