Indicatorii tendintei centrale

Indicatorii tendintei centrale

Indicatorii tendintei centrale cu ajutorul carora se poate caracteriza o serie de repartitie sunt mediile si indicatorii de pozitie.

1. Mediile

Mediile sintetizeaza printr-o expresie numerica ceea ce este tipic si esential, ceea ce se manifesta drept tendinta, legitate in masa de valori individuale ale caracteristicii pentru care se determina.

Media este o valoare reprezentativa, numita si "speranta matematica", spre care tind toate valorile, variatia dintre ele fiind determinata numai de influenta factorilor aleatori.

In vederea obtinerii unei medii reprezentative, trebuie sa se respecte urmatoarele cerinte:

- sa existe un numar suficient de mare de cazuri individuale pentru caracteristica studiata din care se determina media;

- media sa se determine din valori omogene; in caz contrar se vor calcula medii partiale pe subcolectivitati omogene;

- sa se aleaga tipul de medie care sa corespunda cel mai bine formei de manifestare a caracteristicii studiate.

In practica statistica, data fiind diversitatea fenomenelor, se utilizeaza mai multe tipuri de medii:

media aritmetica;

media armonica;

media patratica;

media geometrica;

media cronologica.

Toate aceste medii se pot calcula ca medii simple sau ca medii ponderate.

Mediile simple se determina in cazul in care numarul variantelor valorilor caracteristicii, este egal cu numarul de unitati statistice.

Mediile ponderate se calculeaza cand pentru fiecare varianta a valorilor caracteristicii exista frecventa.

1. Media aritmetica se foloseste, in general, atunci cand fenomenul studiat prezinta modificari aproximativ constante, apropiate de forma unei progresii aritmetice.

Media aritmetica reprezinta acea valoare la care ar fi ajuns fiecare unitate statistica, daca toti factorii de influenta ar fi actionat in mod constant.

Daca media aritmetica este o valoare reprezentativa pentru ansamblul datelor individuale, inseamna ca este acea marime, cu care daca s-ar inlocui valorile individuale ale caracteristicii, suma acestora ar ramane constanta.

Fie o colectivitate statistica alcatuita din n unitati statistice, pentru care

s-au inregistrat valorile unei caracteristici discrete notate cu x_i, x_2,.,x_i,.,x_n. Media aritmetica simpla se determina ca raport intre suma termenilor x_i si numarul de termeni (n) dupa formula:

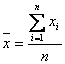
Daca fiecare valoare individuala x_i, ar fi inlocuita cu media aritmetica, valoarea totalizata a caracteristicii la nivelul colectivitatii nu se modifica:

In cazul in care pentru valorile individuale se inregistreaza frecvente absolute, notate f₁, f₂, .,f_i,.,f_n se obtine seria:

x₁ x₂ . x_i. x_n

X:   

f₁ f₂ . f_i .f_n

unde i=1,2,.,n

iar media se determina cu ajutorul mediei aritmetice ponderate pe baza frecventelor absolute sau a frecventelor relative, dupa caz:

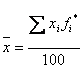
unde f_i^* se determina dupa formula:

O varianta a mediei aritmetice ponderate se utilizeaza pentru a determina nivelul mediu a unei caracteristici alternative. In acest caz, pentru a exprima numeric aceasta caracteristica, in mod conventional, se acorda variantelor formei directe, valoarea "1", iar variantelor formei opuse, valoarea "0".

Schematic, metoda de calcul se prezinta in urmatorul tabel:

Frecventele relative pentru forma directa si pentru forma opusa se obtin dupa urmatoarele formule:

Asadar, media caracteristicii alternative se calculeaza astfel:

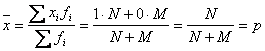
Media caracteristicii alternative se poate exprima si in procente.

Media aritmetica prezinta o serie de proprietati, dintre care in practica statistica se utilizeaza urmatoarele:

Intr-un sir de valori egale, media aritmetica este egala cu fiecare dintre ele. Deci,

x₁ = x₂ = . = x_i = . = x_n = x_c=x, deoarece

Marimea mediei aritmetice este intotdeauna cuprinsa in intervalul de variatie al caracteristicii studiate:

x_min£ x £ x_max

Pentru o serie de distributie cu frecvente, media se incadreaza intre valorile extreme ale caracteristicii, osciland in jurul valorii cu frecventa cea mai mare.

3) Intr-o serie statistica, suma abaterilor individuale ale termenilor seriei de la valoarea mediei lor aritmetice este egala cu zero, atat pentru o serie simpla cat si pentru o serie cu frecvente.

In cazul unei serii simple:

In cazul unei serii cu frecvente:

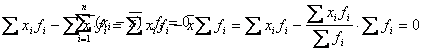
4) Intr-o serie statistica, daca toti termenii se maresc sau se micsoreaza cu o constanta "a", atunci media noilor termeni este mai mica sau mai mare decat media seriei intiale, cu marimea constantei "a".

5) Daca toti termenii unei serii se micsoreaza sau se maresc de h ori, atunci media se mareste sau se micsoreaza de h ori.

Fie xi, i=1,.n, termenii seriei pentru care s-a calculat media aritmetica si x' =x_i/h , I=1,2,.,n termenii modificati ai seriei.

Atunci:

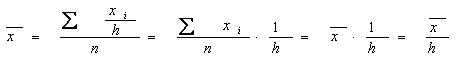
Aceeasi proprietate se verifica si in cazul in care se inmultesc termenii seriei cu o constanta h:

Proprietatile 4 si 5 se folosesc combinat, obtinandu-se relatia de calcul simplificat a mediei aritmetice , atat pentru o serie simpla cat si pentru o serie cu frecvente, pe baza urmatoarelor formule:

- pentru o serie simpla:

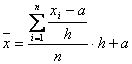
a - este egala cu centrul de interval cu frecventa maxima;

h - lungimea unui interval.

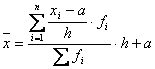
- pentru o serie cu frecvente absolute:

- pentru o serie cu frecvente relative:

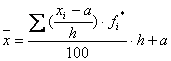
6) Daca intr-o serie de distributie cu frecvente, se reduc proportional toate frecventele, atunci media calculata pe baza noilor frecvente va fi egala cu media seriei initiale.

Fie media seriei initiale:

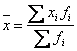
Iar f_i - frecventele micsorate:

7) Pentru o serie de repartitie cu frecventele egale intre ele, media aritmetica ponderata se transforma in medie aritmetica simpla.

Daca f₁=f₂=.=f_I=.=f_n=f_c, Atunci:

8). Intr-o colectivitate structurata pe grupe, media acesteia este dependenta de media grupelor si de frecventele grupelor respective.

Fie seria

x₁ x_{2 .} x_i.x_n impartita in doua grupe:

X:

f₁ f₂ .f_i.f_n

respectiv    x₁ x_{2 .} x_k avand media x_A si numarul

X_A:

f₁ f_{2 .} f_k de unitati f_A

si X_B: x_k*1 x_k*2.x_n

avand media x_B si numarul de

f_k*1 f_k*2.f_n unitati f_B

Atunci, media la nivelul intregii colectivitati va fi:

Unde mediile celor doua grupe se calculeaza astfel:

9) Media aritmetica a sumei sau diferentei dintre doua caracteristici aleatoare independente este egala cu suma sau diferenta mediilor celor doua caracteristici.

Fie x_i, y_i valorile generale a doua caracteristici, ce formeaza doua serii cu numar egal de termeni, cu mediile celor doua caracteristici cunoscute, atunci:

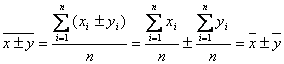
10). Media produsului a doua caracteristici independente x si y este egala cu produsul mediilor celor doua caracteristici.

Aceasta proprietate se utilizeaza atunci cand o caracteristica complexa se poate exprima ca produs de doua sau mai multe caracteristici independente.

2.Media armonica, x_h, se calculeaza din valorile inverse ale termenilor unei serii.

In cazul unei serii simple, media armonica se determina astfel:

Daca inlocuim termenii cu media lor se obtine:

Pentru o serie cu frecvente absolute, media armonica are urmatoarea formula:

Pentru o serie cu frecvente relative, x_h are formula generala:

Media armonica se determina in cazul in care se studiaza o serie bidimensionala, care cuprinde valorile a duoa caracteristici x_i, y_i intre care exista un raport de inversa proportionalitate x_i=1/y_i. Pentru a pastra acest raport si in ce priveste mediile pentru una dintre caracteristici, media se va determina cu ajutorul mediei aritmetice, iar pentru cealalta cu ajutorul mediei armonice.

Daca este calculata din aceleasi valori pozitive, media armonica este intotdeauna mai mica decat media aritmetica.

3. Media patratica (x_p) se calculeaza din patratul valorilor termenilor seriei:

inlocuind termenii cu media lor patratica se obtine:

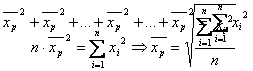
Pentru seriile de repartitie cu frecvente, media patratica ponderata se calculeaza cu urmatoarele formule:

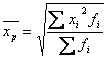
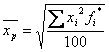
-din frecvente absolute: -din frecvente relative:

Media patratica se foloseste in cazul in care predomina termenii cu valori mari ai seriei, seria fiind asimetrica catre valori mari.

In practica statistica, media patratica se utilizeaza pentru calcularea abaterii standard.

Determinata din aceleasi valori ca si media aritmetica, media patratica este intotdeauna mai mare.

4.Media geometrica (x_g), se calculeaza in cazul in care intre termenii unei serii exista relatie de produs sau cand fenomenul studiat are o evolutie exponentiala, apropiata de forma unei progresii geometrice.

In acest caz, media geometrica reprezinta acea valoare cu care, daca se inlocuiesc termenii seriei, produsul acestora nu se modifica.

Produsul termenilor unei serii se exprima matematic:

Inlocuind termenii cu media geometrica, se obtine:

Formula mediei geometrice simpla este:   

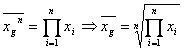
Pentru o serie de repartitie cu frecvente, se utilizeaza media geometrica ponderata, fie pe baza frecventelor absolute, fie a celor relative:

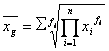
Expresiile mediei geometrice se pot logaritma si se obtin urmatoarele formule:

Prin logaritmare, media geometrica se transforma in logaritmul mediei aritmetice.

Media geometrica se utilizeaza atunci cand seria prezinta variatii foarte mari intre termeni, variatie ce se reduce prin logaritmare, astfel incat valorile mai mici vor fi mai bine reprezentate in valoarea mediei.

Media geometrica nu se poate determina in cazul in care unul dintre termeni este egal cu zero sau ia valori negative.

Determinata din aceleasi valori, media geometrica este intotdeauna mai mica decat media aritmetica.

5.Media cronologica (x_c) este o forma transformata a mediei aritmetice si este specifica seriilor dinamice.

Intre mediile prezentate exista urmatoarea relatie de inegalitate:

2. Indicatorii medii de pozitie

Indicatorii medii de pozitie au drept scop completarea informatiilor obtinute in urma calcularii nivelului mediu si studiaza variatia caracteristicii, a formei de repartitie a frecventelor si evidentiaza tendinta de aglomerare, de concentrare a frecventelor. Acestia se utilizeaza pentru aprecierea gradului de semnificatie a mediei si pentru determinarea gradului de asimetrie.

Principalii indicatori medii de pozitie sunt:

1). Modul sau valoarea modala;

2). Mediana;

3). Cuartile;

4). Decile;

5). Centile.

1). Modul, numit si "valoare modala" sau "valoare dominanta", notata M_o, reprezinta acea valoare a caracteristicii, ce corespunde celei mai mari frecvente de aparitie.

Pentru o serie de repartitie cu frecvente pe variante, modul se determina printr-o simpla analiza a seriei, stabilind cea mai mare frecventa a seriei si identificand valoarea modala, drept valoarea caracteristicii corespunzatoare celei mai mari frecvente.

Pentru o serie de repartitie cu frecvente pe intervale, se identificantr-o prima etapa intervalul modal, adica intervalul cu fre

Valoarea modala se poate determina dupa una din urmatoarele formule:

In cazul in care frecventele sunt aproximativ simetric distribuite in intervalul modal se utilizeaza prima formula, iar daca frecventele au o distributie neuniforma se foloseste cea de-a doua formula.

x^inf_Mo - limita inferioara a intervalului modal

x^sup_Mo - limita superioara a intervalului modal

h_Mo - lungimea intervalului modal h_Mo=x^sup_Mo - x^inf_Mo

D - diferenta dintre frecventa intervalului modal si frecventa intervalului precedent

D - diferenta dintre frecventa intervalului modal si frecventa intervalului urmator.

2. Cuantilele sunt indicatori cu ajutorul carora se realizeaza divizarea seriei intr-un numar de parti egale. Cuantilele de ordin "r" sunt valori ale caracteristicii studiate, ce impart seria statistica ordonata in "r" parti egale. Astfel, daca:

r=2; se obtine cuantila de ordinul 2, numita mediana;

r=4; se obtin cuantile de ordin 4, numite cuartile;

r=10; se obtin cuantile de ordin 10, numite decile;

r=100; se obtin cuantile de ordin 100, numite centile.

2.1. Mediana (M_e) este valoarea situata in mijlocul unei serii ordonate crescator sau descrescator si care imparte seria in doua parti egale.

Determinarea medianei presupune ordonarea termenilor seriei crescator sau descrescator, stabilirea locului medianei si calcularea valorii medianei.

Intr-o serie simpla, formata dintr-un numar impar de termeni, mediana va fi egala cu valoarea termenului central, de rang (n+1)/2, unde n este numarul total de termeni.

Intr-o serie simpla cu un numar par de termeni, mediana va fi media aritmetica simpla a celor doi termeni centrali, de rang n/2 si de rang (n+2)/2.

In cazul seriilor de repartitie cu frecvente, pe variante, mediana este considerata valoarea caracteristicii corespunzatoare primei frecvente cumulate ascendent, ce depaseste (Sf_i+1)/2, unde Sf_i este numarul total de unitati statistice.

In anumite situatii, semnificatia medianei sufera uneori din cauza modului de determinare si se recomanda renuntarea la mediana si alegerea altei valori tipice pentru caracterizarea tendintei centrale.

Pentru o serie de repartitie cu frecvente pe intervale, mediana se determina astfel:

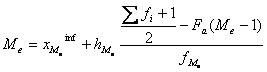
- se identifica intervalul median, adica intervalul de grupare ce corespunde primei frecvente cumulate ascendent ce depaseste (Sf_I+1)/2;

- se determina valoarea medianei folosind relatia de calcul:

unde:

x_Me^inf - limita inferioara a intervalului median

h_Me - lungimea intervalului median

f_Me - frecventa absoluta a intervalului median

Sf_i - suma totala a frecventelor absolute

F_a(M_e- 1) - frecventele cumulate ascendent pana la intervalul median.

2.2.Cuartilele (in numar de trei Q_1, Q₂ = M_e, Q₃) sunt acele valori ale caracteristicii, ce impart seria ordonata crescator sau descrescator in patru parti egale, continand fiecare 25% din numarul observatiilor.

Pentru o serie simpla, cuartilele se determina astfel:

- se stabileste locul cuartilelor cu ajutorul urmatoarelor expresii:

(n + 1)/4 - pentru Q₁; 2(n + 1)/4 - pentru Q₂; 3(n +1)/4 - pentru Q₃

In cazul unei serii simple cu un numar impar de termeni, cuartilele sunt egale cu variantele caracteristicii ce au numar de ordine egal cu expresiile determinate anterior.

Pentru seriile simple cu numar par de termeni, cuartilele se calculeaza ca o medie aritmetica a termenilor vecini pozitiilor aflate pe baza expresiilor determinate anterior.

Intr-o serie de repartitie pe intervale, cuartilele se calculeaza astfel:

- se identifica intervalele in care se situeaza Q₁, Q₂, si Q₃; acestea vor fi intervalele corespunzatoare primelor frecvente cumulate ascendent, ce depasesc expresiile precizate la seriile pe variante.

Locul pentru cuartila Q₁ se determina pe baza relatiei:

iar valoarea cuartilei Q₁ este acea valoare a caracteristicii corespunzatoare primei frecvente cumulate ascendent mai mare sau egala cu expresia :

Sf_i + 1).

Cuartila Q₂ este egala cu M_e, locul acesteia se obtine pe baza relatiei:

Cuartila Q₃ este considerata valoarea caracteristicii corespunzatoare primei frecvente cumulate ascendent ³ ¾(Sf_i+1).

Valorile cuartilelor se determina dupa urmatoarele relatii:

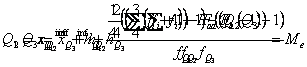
unde: x_Q1^inf, x_Q2^inf, x_Q3^inf - limita inferioara a intervalului in care se gaseste Q₁, Q₂, Q_3;

h_Q1, h_Q2, h_Q3 - lungimea intervalului in care se gaseste Q₁, Q₂, Q_3;

f_Q1, f_Q2, f_Q3 - frecventa absoluta a intervalului in care se gaseste Q₁, Q₂, Q_3;

F_a(Q₁- 1); F_a(Q₂-1); F_a(Q₃-1) - frecventele cumulate pana la intervalul precedent cuartilelor respective.

2.3.Decilele (in numar de noua: D₁, D₂, D₃, D₄, D₅=M_e, D₆, D₇, D₈, D₉) sunt acele valori ale caracteristicii ce impart seria in zece parti egale, continand fiecare 10% din numarul observatiilor.

In cazul unei serii simple, ordonate crescator sau descrescator, decilele se determina conform definitiei.

Pentru seriile de repartitie cu frecvente pe variante, cele doua decile D_K, K=1,2,3,.9, vor fi, pe rand, acele valori ale caracteristicii corespunzatoare primei frecvente cumulate ascendent, ce depaseste expresia: K/10(Sf_i+1); K=1,2,3,.9.

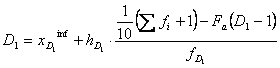
Pentru seriile de repartitii cu frecvente pe intervale, decilele se determina dupa formulele urmatoare:

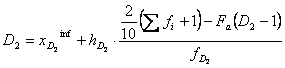
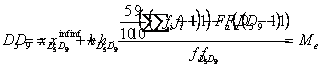
Notatiile sunt asemanatoare cu cele de la cuartile.

2.4. Centilele se determina asemanator cuartilelor si decilelor, calculul lor justificandu-se in cazul fenomenelor ce prezinta variatii mari si foarte mari ale valorilor individuale, cum ar fi: fenomene demografice, clasamente in economia mondiala. Ele sunt in numar de 99, impart variantele unei caracteristici in 100 parti egale cu K/100; K= 1,2,399.