| CATEGORII DOCUMENTE |
| Statistica |
|
|
Testarea parametrilor variabilelor cantitative |
Testele statistice prezentate in acest capitol sunt considerate ca fiind cele mai utilizate. Aceasta popularitate a lor este datorata puterii acestora si simplitatii cu care se calculeaza statisticile acestora.
Pentru aplicarea lor este necesar ca esantioanele studiate sa fie selectate printr-un procedeu aleator. Respectarea acestei cerinte este foarte importanta deoarece ne asigura ca variabilitatea de esantionare este singura sursa de eroare in rezultatele obtinute. Daca aceasta premiza nu este respectata estimatorii obtinuti pot fi deplasati si pot compromite rezultatele.
1. Teste statistice utilizate pentru compararea mediei selectiei cu cea a populatiei
De cele mai multe ori in practica se pune problema testarii ipotezelor cu privire la mediile variabilelor selectiilor. In practica sondajelor orice chestionar va cuprinde si intrebari de identificare utilizate pentru constituirea variabilelor auxiliare. Acest grup de teste are drept scop compararea estimatorilor variabilelor auxiliare calculati pe baza datelor din sondaj cu parametrii corespunzatori, cunoscuti ai populatiei. Daca diferentele sunt semnificative se poate afirma ca esantionul nu este reprezentativ.
In functie de informatiile detinute si de marimea esantionului se utilizeaza un anumit test statistic. Schema decizionala privind alegerea testului este prezentata in figura 1.

1.1 Testul z pentru compararea mediei esantionului cu media populatiei (z one-sample)
Se utilizeaza in cazul in care populatia este exact sau aproximativ normal distribuita. Se poate utiliza si in cazul in care populatia nu este normal sau aproximativ normal distribuita sau nu se cunoaste forma repartitiei populatiei dar esantionul este de volum normal (conform teoremei limite centrale).
Testul se bazeaza pe o statistica a
carei repartitie este normal distribuita cu parametrii ![]() =0 si σ2=1. In functie de modul de
definire a regiunii critice testul poate
fi bilateral, unilateral dreapta sau unilateral stanga.
=0 si σ2=1. In functie de modul de
definire a regiunii critice testul poate
fi bilateral, unilateral dreapta sau unilateral stanga.
A) Test bilateral
In aceasta forma a testului se determina doua limite si se utilizeaza in cazul in care caracteristica este dublu tolerata (figura nr. 2). Aceasta este formata din ariile distributiei situate la extremitati (cele doua cozi ale acesteia) delimitate de valoarea critica zc (Anexa 1 Valorile functiei Gauss Laplace). Prin conventie marimea regiunii critice este raportata la a, proportia regiunii critice in aria totala. In exemplul prezentat in figura 2 nivelul de semnificatie ales este a corespunzator unei probabilitati de garantare a rezultatelor de 0,95. Pentru acest nivel de semnificatie zc =1,96.
Figura 2 Regiunea critica in cazul testului bilateral

Ipotezele testului
sunt: H0: ![]() =
= ![]() si H1:
si H1: ![]()
![]() .
.
Statistica testului
este: 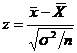 relatia
1
relatia
1
![]() = este
media teoretica (respectiv media populatiei totale);
= este
media teoretica (respectiv media populatiei totale);
![]() = media selectiei;
= media selectiei;
n = volumul esantionului;
σ2 = dispersia teoretica.
In cazul in care nu se cunoaste dispersia teoretica dar esantionul este de volum normal si provine dintr-o populatie normal sau aproximativ normal distribuita aceasta poate fi inlocuita cu dispersia esantionului.
Plecand de la forma testului putem construi doua limite z1 si z2 astfel incat pentru un nivel de semnificatie α fixat sa avem:
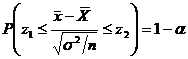
Daca
z1=z2 obtinem: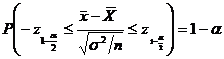
Regiunea
critica in cazul testului bilateral este: W: 
Daca
valoarea calculata zc luata in modul este inferioara
valorii tabelate corespunzatoare nivelului de semnificatie putem
considera ca nu exista diferente semnificative intre ![]() si
si ![]() si se accepta ipoteza nula.
si se accepta ipoteza nula.
B) Test unilateral stanga
In anumite situatii cercetatorul este interesat sa evidentieze existenta diferentelor semnificative intr-o singura directie recurgand la teste unilaterale.
Figura 3 Regiunea critica in cazul testului unilateral stanga
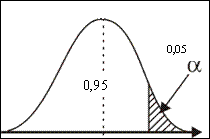
In cazul acesta plasam regiunea critica doar in una din extremitatile distributiei in functie de sensul testului unilateral. Daca in situatia testului bilateral pentru un nivel de semnificatie a=0,05 valoarea critica zc =1,96 in situatia testului unilateral, pentru acelasi nivel de semnificatie zc =+1,65 in cazul in care este regiunea critica este formata din extremitatea (coada) superioara a distributiei (test unilateral stanga - figura 3) si zc = -1,65 pentru regiunea critica situata la extremitatea inferioara (test unilateral dreapta - figura 4).
Ipotezele testului
unilateral stanga sunt: H0: ![]()
![]() si H1:
si H1: ![]() <
< ![]() .
.
Regiunea
critica este: W: 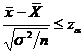 (reprezentata in
figura 3)
(reprezentata in
figura 3)
Daca valoarea calculata zc este mai mica decat valoarea tabelata corespunzatoare nivelului de semnificatie se respinge ipoteza nula si se accepta ipoteza alternativa.
C) test unilateral dreapta
Ipotezele testului
sunt:H0: ![]()
![]() si H1:
si H1: ![]() >
> ![]() .
.
Regiunea
critica este: W: 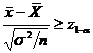 (figura 4)
(figura 4)
Daca valoarea calculata zc este mai mare decat valoarea tabelata corespunzatoare nivelului de semnificatie se respinge ipoteza nula si se accepta ipoteza alternativa.
1.2. Testul t pentru compararea mediei esantionului cu media populatiei (Student one-sample)
In cazul in care nu se cunoaste dispersia populatiei aceasta poate fi inlocuita cu dispersia esantionului. In aceasta situatie daca populatia este normal sau aproximativ normal distribuita iar volumul esantionului este de volum redus se utilizeaza pentru compararea mediei esantionului cu media populatiei testul Student.
Acest test se poate utiliza si atunci cand nu se cunoaste dispersia teoretica, populatia nu este normal distribuita dar esantionul este de volum normal.
Ca si in cazul testului z, in functie de modul de definire a regiunii critice testul t poate fi bilateral, unilateral dreapta sau unilateral stanga.
A) Test bilateral
Ca si in cazul testului z, in aceasta forma a testului se determina doua limite si se utilizeaza in cazul in care caracteristica este dublu tolerata.
Ipotezele testului bilateral sunt:
H0: ![]() =
= ![]() si H1:
si H1: ![]()
![]()
Statistica testului
este: 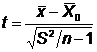 relatia
2
relatia
2
S2 = dispersia esantionului iar restul notatiilor sunt cele utilizate la testul precedent.
Regiunea
critica in cazul testului bilateral este: W: 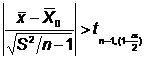
Daca
valoarea calculata tc luata in modul, este inferioara
valorii tabelate corespunzatoare numarului de grade de libertate
(df=n-1) si nivelului de semnificatie putem considera ca nu
exista diferente semnificative intre ![]() si
si ![]() si se accepta ipoteza nula.
si se accepta ipoteza nula.
B) test unilateral stanga
Ipotezele testului unilateral stanga sunt:
H0: ![]()
![]() si H1:
si H1:
![]() <
< ![]() Regiunea critica
este: W:
Regiunea critica
este: W: 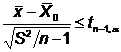
Daca valoarea calculata tc este mai mica decat valoarea tabelata corespunzatoare numarului de grade de libertate si nivelului de semnificatie se respinge ipoteza nula si se accepta ipoteza alternativa.
C) test unilateral dreapta
Ipotezele testului unilateral dreapta sunt:
H0: ![]()
![]() si H1:
si H1: ![]() >
> ![]() . Regiunea critica este: W:
. Regiunea critica este: W: 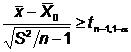
Daca valoarea calculata zc este mai mare decat valoarea tabelata corespunzatoare numarului de grade de libertate si nivelului de semnificatie se respinge ipoteza nula si se accepta ipoteza alternativa.
1. Compararea mediei esantionului cu media populatiei sub SPSS (one-sample T Test).
Pentru efectuarea testului sub SPSS se selecteaza optiunea One-Sample Test din Analyze/Compare Means. (figura 4).
Figura nr. 4 Selectarea testului One Sample T Test
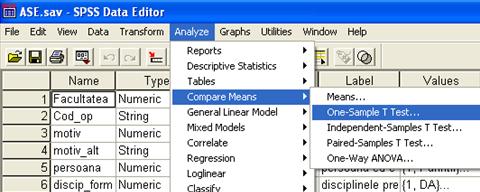
Pentru a exemplifica modul de interpretarea a tabelelor outpulului vom lua urmatorul exemplu:
S-a realizat un sondaj simplu aleator pe un esantion de 643 de studenti din ASE, an terminal. Se cunoaste din surse administrative ca media pe anul precedent a fost 7,4. Sa se verifice daca exista diferente semnificative intre media selectiei si media populatiei.
Efectuand comanda Analyze/Compare Means/ One-Sample Test s-au obtinut tabelele 1 (contine principalii indicatori statistici calculati pentru esantion) si 2 (rezultatele aplicarii testului).
Tabel 1. One-Sample Statistics
|
N |
Mean |
Std. Deviation |
Std. Error Mean |
||
|
Media | |||||
|
Interpretare |
Nume variabila |
Volum esantion |
Media selectiei |
Abaterea medie patratica |
Eroarea de reprezentativitate |
Tabel 2. One-Sample Test
|
Test Value = 7.4 (valoarea mediei in populatie) |
||||||
|
df |
Sig. (2-tailed) |
Mean Difference |
95% Confidence Interval of the Difference |
|||
| Lower |
Upper |
|||||
|
Media | ||||||
Premizele in care de face testatrea ipotezei sunt:
esantionul este selectat aleator;
variabila este numerica;
dispersie in populatie necunoscuta substituita cu estimatorul acesteia dispersia selectiei :
esantion de volum normal.
Se va efectua testul z one-sample
Ipotezele testului
bilateral sunt: H0: ![]() =
= ![]() si H1:
si H1: ![]()
![]() .
.
Interpretarea fiecarei valori din tabelul 2:
Valoarea calculata a testului. SPSS ne returneaza valoarea calculata conform statisticii testului. Aplicand relatia de calcul 1 obtine, acelasi rezultat.
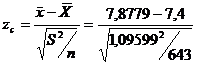 =11,057
=11,057
df. Numarul de grade de libertate. Prezinta importanta doar in situatia esantioanelor de volum redus cand se aplica testul Student one-sample pentru a stabili valoarea critica.
Sig. (2-tailed). Nivelul de semnificatie a in cazul testului bilateral. Probabilitatea cu care se respinge H0 se calculeaza ca 1-a Pentru a respinge H0cu o probabilitate de 0,95 este necesar ca a sa fie cel putin 0,05. In caz contrar se considera ca nu exisa diferente semnificative.
In exemplul nostru se respinge H0cu o probabilitate de 0,999999.
Daca dorim sa efectuam un test unilateral valoarea critica se preia din Anexa1 pentru probabilitatea cu care dorim sa garantam rezultatele.
Mean Difference. Reprezinta diferenta dintre media esantionului si cea teoretica.
95% Confidence Interval of the Difference. Intervalul de incredere al diferentei dintre medii. Probabilitatea pentru care este calculate intervalul poate fi stabilita selectand Options din fereastra de comanda a testului (figura 5).
Figura nr. 5 Fereastra de definire a optiunilor testului
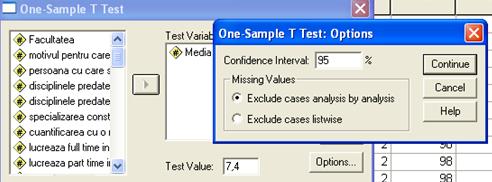
1.4 Aplicatii pentru verificarea ipotezelor privind media selectiei si media populatie
Aplicatia 1
S-a realizat un sondaj aleator in randul salariatilor unei companii pe un esantion de 90 persoane. In urma centralizarii si prelucrarii datelor pentru variabila auxiliara "Vechimea medie" s-a calculat nivelul mediu de 7,2 ani iar dispersia variabilei este de 1,42.
Se cere:
Rezolvare
Pentru a vedea daca exista diferente semnificative ale medie selectiei fata de valoarea cunoscuta din populatie se utilizeaza testul z deoarece sunt respectate urmatoarele premize (vezi schema din figura nr. 1):
esantionul este selectat aleator;
variabila este numerica;
dispersie in populatie necunoscuta substituita cu estimatorul acesteia dispersia selectiei :
esantion de volum normal.
Ipotezele testului
bilateral sunt: H0: ![]() =
= ![]() si H1:
si H1: ![]()
![]() .
.
Regiunea critica in cazul testului bilateral este data de relatia:
W: 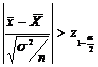
Valoarea
calculata a testului este: 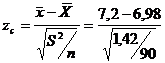 =1,75
=1,75
Valoarea calculata luata in valoare absoluta se compara cu cea teoretica de 1,96 corespunzatoare nivelului de semnificatie ales (a=0,05) si, deoarece este mai mica decat aceasta se accepta ipoteza nula concluzionandu-se ca esantionul este reprezentativ.
![]() Premizele in care de face testatrea ipotezei sunt:
Premizele in care de face testatrea ipotezei sunt:
esantionul este selectat aleator;
variabila este numerica;
dispersie in populatie necunoscuta substituita cu estimatorul acesteia dispersia selectiei :
esantion de volum redus
In consecinta se va aplica testul Student one-sample.
Ipotezele testului
bilateral sunt: H0: ![]() =
= ![]() si H1:
si H1: ![]()
![]() .
.
Regiunea critica in cazul testului bilateral este data de relatia:
W: 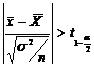
Valoarea
calculata a testului este: 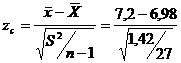 =0,96
=0,96
Valoarea calculata luata in valoare absoluta se compara cu cea teoretica de 2,05 corespunzatoare nivelului de semnificatie ales (a=0,05) si numarului de grade de libertate df=28-1. Deoarece este mai mica decat aceasta se accepta ipoteza diferentei nule.
Aplicatia 2
In randul salariatilor unei societati comerciale din sectorul energetic s-a realizat un sondaj simplu aleator pe un esantion de 160 persoane.
Estimatorul varstei medii a salariatilor este 36,4 ani cu o abatere medie patratica de 9,46 ani iar parametrul corespunzator din populatie este de 35,1 ani.
Sa se testeze ipoteza diferentei nule intre media selectiei si cea a populatiei totale utilizand programul SPSS.
Rezolvare
Premizele in care de face testatrea ipotezei sunt:
esantionul este selectat aleator;
variabila este numerica;
dispersie in populatie necunoscuta substituita cu estimatorul acesteia dispersia selectiei :
esantion de volum normal.
Vom efectua testul z one-sample
Ipotezele testului
bilateral sunt: H0: ![]() =
= ![]() si H1:
si H1: ![]()
![]() .
.
Efectuand testul cu ajutorul programului SPSS, output-ul acestuia este:

Valoarea calculata a testului returnata de SPSS este de 1,799, fiind mai mica decat cea teoretica de 1,96. Nivelul de semnificatie a= 0,074 este mai mare de 0,05. In consecinta se accepta ipoteza diferentei nule dintre media selectiei si media teoretica.
2. Teste statistice utilizate pentru verificarea ipotezelor privind mediile a doua grupuri
In analiza statistico econometrica a fenomenelor din sfera economica, politica si sociala se pune problema compararii mediilor unor caracteristici numerice pentru diferite grupuri.
In principal aceste teste se impart in doua categorii, in functie de modul in care au fost selectate esantioanele: teste pentru esantioane independente si teste pentru esantioane dependente. In ambele situatii este absolut necesar ca procedeul de selectie a unitatilor in esantioane sa fie aleator.
2.1. Compararea mediilor provenite din doua esantioane independente
Prin esantioane independente se intelege ca procedeul de selectie al unui esantion nu este asociat cu procedeul de selectie al celuilalt esantion. De exemplu, cu ajutorul acestor teste putem verifica daca exista diferente semnificative intre diferitele categorii ale fortei de munca in teritorial, institutional sau sectorial.
Realizarea acestei comparatii imbraca mai multe forme in functie de conditiile existente (marimea esantioanelor, forma distributiilor, cunoasterea variatiei caracteristicilor studiate in populatie).
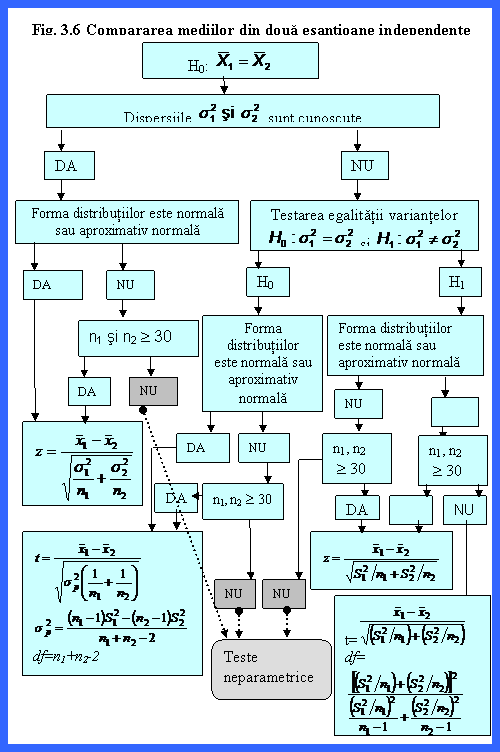
Schema decizionala a alegerii testului adecvat am prezentat-o sugestiv in figura nr. 6.
Procedura prin care se realizeaza testele de semnificatie din acest subcapitol este foarte asemanatoare celei utilizate in subcapitolul precedent. In functie de modul de definire a regiunii critice testele pot fi bilaterale, unilaterale dreapta sau unilaterale stanga.
In cazul in care dispersiile caracteristicilor in populatii s si s nu se cunosc se va utiliza mai intai un test pentru verificarea egalitatii variantelor (subcapitolul 2.). In functie de rezultat (vezi figura 6) se va opta pentru un anumit test statistic in vederea compararii mediilor.
2.1.1. Utilizarea testului z pentru compararea a doua medii
Se
poate utiliza atunci cand cele doua variabile sunt normal repartizate (X1~N(![]() ) si X2~N(
) si X2~N(![]() ) sau cele doua
esantioane sunt de volum normal (n1 si n2
>30) deoarece conform legii numerelor mari in teoria sondajului se
demonstreaza ca daca volumul esantionului este suficient de
mare media de sondaj urmeaza o distributie
normala a carei medie este
chiar media populatiei totale.
) sau cele doua
esantioane sunt de volum normal (n1 si n2
>30) deoarece conform legii numerelor mari in teoria sondajului se
demonstreaza ca daca volumul esantionului este suficient de
mare media de sondaj urmeaza o distributie
normala a carei medie este
chiar media populatiei totale.
Statistica
testului este: 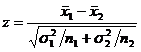 relatia
3
relatia
3
![]() = mediile selectiilor din cele doua
esantioane independente;
= mediile selectiilor din cele doua
esantioane independente;
n1 si n2 = volumul esantioanelor;
![]() = dispersiile cunoscute ale populatiilor;
= dispersiile cunoscute ale populatiilor;
In cazul in care nu se cunoaste dispersia teoretica dar esantioanele sunt de volum normal si provin din populatii normal sau aproximativ normal repartizate acestea pot fi inlocuite cu estimatiile acestora, dispersiile esantioanelor (in ipoteza s1 s2
A) test bilateral
In aceasta forma a testului se determina doua limite si se utilizeaza in cazul in care caracteristica este dublu tolerata.
Ipotezele testului sunt:
H0: ![]() -
-![]() =0 sau
=0 sau ![]() =
=![]() si H1:
si H1: ![]() -
-![]() ≠0 sau
≠0 sau ![]() ≠
≠![]()
In cazul in care nu se cunoaste dispersia teoretica dar esantioanele sunt de volum normal si provin din populatii normal sau aproximativ normal repartizate acestea pot fi inlocuite cu estimatiile acestora, dispersiile esantioanelor.
Regiunea
critica este:W: 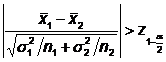
Daca
valoarea calculata zc luata in modul este inferioara
valorii tabelate corespunzatoare nivelului de semnificatie putem
considera ca nu exista diferente semnificative intre ![]() si
si ![]() , acceptandu-se ipoteza nula.
, acceptandu-se ipoteza nula.
B) test unilateral stanga
H0:
![]() ≥
≥![]() si H1:
si H1: ![]() <
<![]()
Regiunea
critica este: W: 
Daca valoarea calculata zc este mai mica decat valoarea tabelata corespunzatoare nivelului de semnificatie se respinge ipoteza nula si se accepta ipoteza alternativa.
C) test unilateral dreapta
H0:
![]() ≤
≤![]() si H1:
si H1: ![]() >
>![]()
Regiunea
critica este: W: 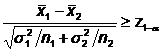
Daca valoarea calculata zc este mai mare decat valoarea tabelata corespunzatoare nivelului de semnificatie se respinge ipoteza nula si se accepta ipoteza alternativa.
2.1.2. Testul "t" pentru verificarea egalitatii a doua medii (s1,s2 necunoscute cu s1 s2) pentru esantioane de volum redus
Se
poate utiliza atunci cand cele doua variabile sunt normal repartizate (X1~N(![]() ) si X2~N(
) si X2~N(![]() )) dar dispersiile teoretice (diferite) nu se cunosc.
Deoarece cele doua esantioane sunt de volum redus (n1
si n2 <30) nu ne vom mai putea baza pe teorema limita centrala si deci nu
vom mai pute utiliza testul z pentru testarea diferentei dintre cele
doua medii. In aceste conditii se va utiliza testul Student dar cu o
formula corectata a numarului gradelor de libertate.
Numarul de grade de libertate rezultat in acest caz este mult mai mare
decat in cazul prezumtiei egalitatii dispersiilor.
)) dar dispersiile teoretice (diferite) nu se cunosc.
Deoarece cele doua esantioane sunt de volum redus (n1
si n2 <30) nu ne vom mai putea baza pe teorema limita centrala si deci nu
vom mai pute utiliza testul z pentru testarea diferentei dintre cele
doua medii. In aceste conditii se va utiliza testul Student dar cu o
formula corectata a numarului gradelor de libertate.
Numarul de grade de libertate rezultat in acest caz este mult mai mare
decat in cazul prezumtiei egalitatii dispersiilor.
Statistica
testului este: 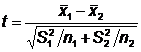 relatia
4
relatia
4
![]() = mediile selectiilor din cele doua
esantioane independente;
= mediile selectiilor din cele doua
esantioane independente;
n1 si n2 = volumul esantioanelor;
![]() = estimatiile dispersiilor necunoscute ale
populatiilor.
= estimatiile dispersiilor necunoscute ale
populatiilor.
Desi statistica este asemanatoare cu cea a testului z (relatia 3) se utilizeaza o alta formula pentru calcularea numarului de grade de libertate si anume:
dfWelch 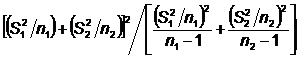
Aceasta este cunoscuta in literatura de specialitate drept corectia Welch si a fost conceputa pentru constructia unui test puternic in prezenta inegalitatii dispersiilor in populatiile analizate.
Relatia corectata a numarului de grade de libertate duce intotdeauna la o valoare mai mica decat cea folosita pentru esantioane de volum normal
In functie de modul de definire a regiunii critice testele pot fi bilaterale, unilaterale dreapta sau unilaterale stanga.
2.1. Testul "t" pentru verificarea egalitatii a doua medii (s1,s2 necunoscute cu s1 s2
Vom utiliza acest test in cazul in care pornim de la ipoteza egalitatii dispersiilor necunoscute (este acceptata ipoteza s1 s2 in urma efectuarii unuia din testele din subcapitolul 2.3) si a normalitatii distributiilor (aceasta conditie, conforma teoremei limitei centrale, este mai putin importanta pentru esantioanele mari) Desi testul t este de obicei asociat cu esantioanele de volum redus, distributia Student este adecvata in cazul in care variantele sunt necunoscute.
Acest
test porneste de la calcularea unei valori estimate a dispersiei necunoscute
(![]() ) pe care se presupune ca o estimeaza dispersia
fiecarui esantion.
) pe care se presupune ca o estimeaza dispersia
fiecarui esantion.
Statistica testului este: 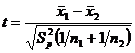 relatia
5
relatia
5
unde ![]()
![]() = mediile selectiilor din cele doua
esantioane independente;
= mediile selectiilor din cele doua
esantioane independente;
n1 si n2 = volumul esantioanelor;
![]() = estimatiile dispersiilor necunoscute ale
populatiilor;
= estimatiile dispersiilor necunoscute ale
populatiilor;
![]() =variatia comuna estimata pe baza dispersiilor
selectiilor.
=variatia comuna estimata pe baza dispersiilor
selectiilor.
Dupa modul de definire a regiunii critice testele pot fi bilaterale, unilaterale dreapta sau stanga. Valoarea calculata a testului se compara cu valoarea corespunzatoare nivelului de semnificatie ales si numarului de grade de libertate df=n1+n2-2.
2.2. Compararea mediilor provenite din doua esantioane dependente
In subcapitolul anterior esantioanele selectiilor respectau conditia de independenta. Uneori ne lovim de situatii in care esantioanele din care provin mediile ce trebuie comparate sunt dependente (procedeul de selectie al unui esantion este legat de procedeul de selectie al celuilalt). De exemplu in cazul in care dorim sa analizam productivitatea individuala a muncii salariatilor inainte si dupa schimbarile realizate la o statie de lucru.
Testele in care esantioanele nu sunt independente sunt mentionate ca teste asupra observatiilor perechi.
Acestea sunt frecvent utilizate in cercetarile aprofundate ale fenomenelor realizate pe baza penelurilor deoarece poate surprinde modificarile survenite in fenomenul analizat la momente diferite de timp sau in urma aplicarii unei proceduri. Mai poate fi utilizat si pentru a compara mediile a doua caracteristici asemanatoare (sunt masurate pe aceeasi scala si iau valori in acelasi interval) dintr-un plan de observare. De exemplu putem verifica cu acest test daca exista diferente semnificative intre scorul obtinut de un grup de indivizi la un test de dexteritate cu cel obtinut de aceeasi indivizi la un test de perspicacitate.
Variabila considerata in acest caz este di=x1i-x2i unde x1i si x2i reprezinta valorile inregistrate pentru unitatea i in esantionul 1 respectiv 2.
Premizele pentru efectuarea testului sunt:
esantioanele au fost selectate aleator;
variabilele sunt masurate pe scala interval sau proportionala;
variabila tuturor diferentelor Di=X1i-X2i urmeaza o distributie normala. Conditie necesara in cazul esantioanelor e volum redus.
Testul este in esenta asemanator celui prin care se realizeaza compararea mediei unui singur esantion cu media teoretica In acest caz formularea ipotezelor este prezentata dupa cum urmeaza:
|
Ipoteza nula H0 |
Ipoteza alternativa H1 |
Tipul testului |
|
M(d)=0 |
M(d)≠0 |
bilateral |
|
M(d)≥0 |
M(d)<0 |
unilateral stanga |
|
M(d)≤0 |
M(d)>0 |
unilateral dreapta |
Statistica testului este:![]() relatia
6
relatia
6
![]() unde:
unde:
![]() =media diferentelor di=x1i-x2i;
=media diferentelor di=x1i-x2i;
n = numarul de observatii perechi
Sd =abaterea standard a variabilei di
Valoarea calculata a testului se compara cu valoarea corespunzatoare nivelului de semnificatie ales si numarului de grade de libertate df=n-1
2. Teste statistice utilizate pentru verificarea ipotezei egalitatii variantelor
De multe ori, in analiza datelor provenite din sondaje statistice, se pune problema compararii mediilor din doua sau mai multe esantioane, pentru a stabili daca exista sau nu diferente semnificative intre ele. Realizarea acestor comparatii imbraca mai multe forme in functie de conditiile existente (marimea esantioanelor, forma distributiilor, cunoasterea variatiei caracteristicilor studiate in populatie).
Testele parametrice utilizate pentru compararea mediilor rezultate din doua sau mai multe esantioane independente pleaca de la urmatoarele premize:
Esantioanele au fost selectate independent;
Populatiile sunt normal distribuite.
Dispersiile populatiilor sunt egale.
Prin esantioane independente se intelege ca procedeul de selectie al unui esantion nu este asociat cu procedeele de selectie ale celorlalte esantioane. Aceasta premiza este usor de verificat prin analiza modului in care au fost selectate elementele esantioanelor.
Normalitatea distributiilor poate fi usor verificata prin analizarea histogramei sau a graficului probabilitatilor normale, realizat de majoritatea programelor statistice. Cand analiza graficelor este neconcludenta se recomanda utilizarea unuia din testele prezentate in subcapitolul aaaaa:
Verificarea normalitatii distributiilor este foarte importanta in cazul esantioanelor de volum redus deoarece, conform Teoremei limitei centrale, esantioanele de volum normal aproximeaza distributia normala.
O larga deviere de la normalitate duce la scaderea puterii si eficientei acelor teste de semnificatie care pornesc de la aceasta conditie.
Premiza egalitatii dispersiilor variabilelor in populatiile din care s-au extras esantioanele este cea mai importanta. Exista mai multe metode de verificare a omogenitatii dispersiilor. In continuare sunt prezentate cateva din cele mai utilizate teste statistice cu ajutorul carora se poate verifica aceasta ipoteza.
Testul F
Este cel mai cunoscut test pentru verificarea ipotezei egalitatii dispersiilor si se foloseste in cazul a doua esantioane independente.
Ca si distributia Student, distributia F apartine familiei distributiilor continue. Spre deosebire de distributia Student a carei forma este determinata de o singura valoare a numarului gradelor de libertate, forma distributiei F este determinata de doua valori diferite ale gradelor de libertate. In termenii procedurii de testare a ipotezelor acest test poate fi descris astfel:
formularea ipotezei nule si a ipotezei alternative:
![]() ;
;
alegerea nivelului de semnificatie a. In tabelele distributiei Fischer-Snedecor sunt reprezentate ariile regiunilor critice pentru a: 0.05; 0,025 si 0,01. Deoarece acestea sunt reprezentate de o singura arie in cazul efectuarii unui test bilateral vor corespunde unor nivele de semnificatie a
Calcularea testului statistic pe baza relatiei:,
![]() sau
sau ![]() ; (relatia
7)
; (relatia
7)
Identificarea valorii critice. Deoarece testul este bilateral se determina o singura valoare critica data de:
![]() unde: a reprezinta nivelul de semnificatie ales
unde: a reprezinta nivelul de semnificatie ales
v1=(n-1) unde n este volumul esantionului care are dispersia mai mare;
v2=(n-1) unde n este volumul esantionul cu dispersia mai mica.
Regula de decizie este: se respinge H0 daca valoarea calculata a testului este mai mare decat valoarea critica. In acest caz nu suntem indreptatiti sa afirmam egalitatea dispersiilor populatiilor.
Testul Hartley
Este un test simplificat in masura sa sesizeze daca cel putin unul din cele k esantioane difera semnificativ de celelalte prin variatia sa.
Fie
xij (i=1,2,..,n+1; j=1,2,..,k) elementele a k selectii
independente efectuate asupra variabilelor normal repartizate Xj~N(![]() )
)

Unde
![]() este calculat pe baza relatiei:
este calculat pe baza relatiei: ![]() cu
cu ![]() reprezinta
estimatii nedeplasate ale dispersiilor populatiilor
reprezinta
estimatii nedeplasate ale dispersiilor populatiilor ![]() . Raportul
. Raportul ![]() urmeaza o
repartitie
urmeaza o
repartitie ![]() . Ipotezele testului sunt:
. Ipotezele testului sunt:
H0:
![]() pentru j=1,.,k;
pentru j=1,.,k;
H1:
![]() astfel incat
astfel incat ![]()
H0
este echivalenta cu multimea ipotezelor: H0(lj): ![]() (l j, 1 l,j k).
(l j, 1 l,j k).
Pentru
oricare doua dispersii ipoteza ![]() poate fi
verificata cu ajutorul testului binecunoscutului test F bazat pe
distributia Fischer-Snedecor
poate fi
verificata cu ajutorul testului binecunoscutului test F bazat pe
distributia Fischer-Snedecor ![]() unde a este nivelul de semnificatie iar numarul de grade de
libertate v1=v2=n. Ipoteza H0(lj):
unde a este nivelul de semnificatie iar numarul de grade de
libertate v1=v2=n. Ipoteza H0(lj): ![]() este acceptata
daca :
este acceptata
daca :
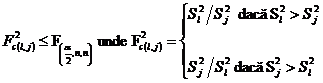
Deoarece
H0 este echivalenta cu multimea ipotezelor H0(lj)
(l j, 1 l,j k) obtinem testul pentru H0 luand intersectia
tuturor celor ![]() regiuni de acceptare
si acceptam H0 daca si numai daca:
regiuni de acceptare
si acceptam H0 daca si numai daca:![]() .
.
Aceasta relatie formeaza testul cunoscut sub denumirea Fmax si este echivalenta cu:
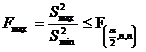 . (relatia 8)
. (relatia 8)
Testul prezinta avantajele: este rapid, usor de calculat si utilizeaza distributia Fischer-Snedecor.
Dezavantajele testului: este afectat de non-normalitatea distributiilor si necesita ca esantioanele sa aiba aceeasi dimensiune.
Fie
nj cu j=1,,k volumul celor k esantioane. Se considera
(Stevens 1990) ca daca raportul ![]() este indeplinita
conditia egalitatii esantioanelor impusa de testul
Hartley.
este indeplinita
conditia egalitatii esantioanelor impusa de testul
Hartley.
Chiar daca aceasta restrictie nu este indeplinita Tabachnik si Fidel (2001) afirma ca testul Fmax se poate utiliza in mod eficient, fara sa fie afectata puterea lui, daca sunt indeplinite conditiile:
![]() ;
;
![]()
Daca
aceste conditii sunt indeplinite, asumarea ipotezei omogenitatii
dispersiilor nu este o problema. Valoarea calculata se compara
cu valoarea teoretica din tabela Fmax corespunzatoare nivelului de
semnificatie α, numarului de esantioane k si
numarului de grade de libertate df=![]() -1. Unde
-1. Unde ![]() se calculeaza ca medie geometrica dupa relatia:
se calculeaza ca medie geometrica dupa relatia:
![]()
![]() Testul Lehman
Testul Lehman
Fie
xij (i=1,2,..,nj; j=1,2,..,k) elementele a k
selectii independente efectuate asupra variabilelor normal repartizate Xj~N(![]() ). Ipotezele testului sunt:
). Ipotezele testului sunt:
H0:
![]() pentru j=1,.,k si
pentru j=1,.,k si
H1: exista ![]() astfel incat
astfel incat ![]()
Lehman, in 1959 a construit statistica:
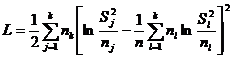 . (relatia
9)
. (relatia
9)
Unde
![]() cu
cu ![]() ; nj= Nj
-1;
; nj= Nj
-1; ![]() .
.
Testul
bazat pe statistica L respinge ipoteza H0
cand valoarea calculata pe baza datelor observate este mai mare
decat o constata fixata. Deoarece statistica L urmeaza la
limita o repartitie ![]() (unde k
reprezinta numarul de esantioane) valoarea constantei cu care se
va cu compara calculata a statisticii L va fi valoarea
(unde k
reprezinta numarul de esantioane) valoarea constantei cu care se
va cu compara calculata a statisticii L va fi valoarea ![]() .
.
Testul Bartlett
Acest test a fost construit de Bartlett in 1957. Deoarece este instabil in cazul non-normalitatii distributiilor se recomanda ca, inaintea aplicarii, sa se realizeze un test de concordanta pentru verificarea normalitatii acestora.
H0: ![]() pentru j=1,.,k
pentru j=1,.,k
H1: ![]() astfel incat
astfel incat ![]()
Statistica testului
este: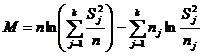 (relatia
10)
(relatia
10)
unde notatiile au aceeasi semnificatie ca si in cazul testului Lehman.
Ca
si in cazul statisticii L, repartitia M tinde asimptotic catre o
repartitie ![]() iar valoarea observata
se va compara cu valoarea teoretica
iar valoarea observata
se va compara cu valoarea teoretica ![]() . Daca M
. Daca M ![]() se accepta H0. In caz contrar re
respinge H0 si se
accepta H1.
se accepta H0. In caz contrar re
respinge H0 si se
accepta H1.
Testul a fost redefinit de Snedecor si Cochran in anul in 1983 sub forma prezentata in continuare.[2] Ipotezele testului sunt aceleasi.Statistica testului este:
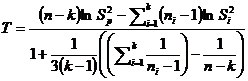 (relatia
11)
(relatia
11)
![]() =variatia esantionului i; ni=volumul
esantionului i; n=
=variatia esantionului i; ni=volumul
esantionului i; n=![]() iar
iar
![]() = estimatia dispersiei definita de relatia:
= estimatia dispersiei definita de relatia: ![]() .
.
Ipoteza
egalitatii variantelor se accepta daca ![]() unde a reprezinta nivelul de semnificatie corespunzator
probabilitatii cu care se vor garanta rezultatele iar numarul de
grade de libertate df=k-1.
unde a reprezinta nivelul de semnificatie corespunzator
probabilitatii cu care se vor garanta rezultatele iar numarul de
grade de libertate df=k-1.
Testul Cochran
Este un test foarte simplu dar are nevoie de premiza unor esantioane de volum egal. Ipotezele testului sunt:
H0:
![]() pentru i=1,.,k si
pentru i=1,.,k si
H1:
![]() astfel incat
astfel incat ![]()
Statistica
testului este:![]() (relatia
12)
(relatia
12)
cu![]() este estimatorul dispersiei din stratul i.
este estimatorul dispersiei din stratul i.
Ipoteza nula se accepta daca G<Gk,n-1,a, valoarea critica luandu-se din tabela valorilor critice ale testului Cochran corespunzatoare nivelului de semnificatie a
Ca si in cazul testului Hartley, pentru a inlatura dezavantajul datorat conditiei ca esantioanele sa fie de volum egal se poate utiliza testul Cochran sub urmatoarea forma modificata:
![]() . (relatia 13)
. (relatia 13)
![]() reprezinta dispersia esantionului de volum maxim.
reprezinta dispersia esantionului de volum maxim.
Testul Levene
Acesta test reprezinta o alternativa a testelor precedente pentru verificarea omogenitatii variantelor si este un test robust chiar si in cazul in care variabilele nu sunt normal sau aproximativ normal repartizate. Daca este indeplinita conditia de normalitate se recomanda utilizarea testului Bartlett, fiind mult mai sensibil in aceste situatii.
Fie xij (i=1,2,..,k; j=1,2,..,ni) elementele unei selectii de volum n impartit in k subgrupuri, fiecare de volum ni. Ipotezele testului sunt:
H0:
![]() pentru i=1,.,k si
pentru i=1,.,k si
H1:
![]() astfel incat
astfel incat ![]() .
.
Statistica testului este:
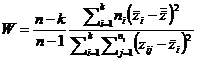 . (relatia
14)
. (relatia
14)
Valoarea zij poate fi definita in urmatoarele trei moduri:
![]() unde
unde ![]() este media subgrupului
i.
este media subgrupului
i.
![]() unde
unde ![]() este mediana
subgrupului i.
este mediana
subgrupului i.
![]() unde
unde ![]() este media
ajustata obtinuta prin eliminarea a 10% din valorile
extreme pentru subgrupul i.
este media
ajustata obtinuta prin eliminarea a 10% din valorile
extreme pentru subgrupul i.
In varianta originala a testului se utiliza doar media in definirea variabilei zij. Brown and Forsythe (1974) au propus o extindere a acestui test prin utilizarea medianei sau a mediei ajustate. In urma studiilor efectuate se indica utilizarea mediei ajustate atunci cand variabila selectiei urmeaza o distributie Cauchy sau a medianei in cazul distributia este asimetrica. Daca distributia este omogena si simetrica se va utiliza media aritmetica. Alegerea optima se realizeaza dupa analizarea formei distributiei.
"Posibilitatea alegerii modului in care in definim variabila zij determina robustetea si puterea testului Levene. Prin robustete se intelege abilitatea testului de a nu detecta in mod fals inegalitatea variantelor atunci cand variabilele nu sunt normal distribuite. Prin puterea testului se intelege abilitatea acestuia de a detecta inegalitatea variantelor atunci cand in mod real sunt inegale"[3].
Ipoteza
nula se accepta daca: ![]() unde
unde ![]() este valoarea
critica a distributiei F pentru numarul de grade de libertate df1=k-1, df2=n-k si nivelul de semnificatie a considerat.
este valoarea
critica a distributiei F pentru numarul de grade de libertate df1=k-1, df2=n-k si nivelul de semnificatie a considerat.
Datorita flexibilitatii si robustetii sale, acest test este utilizat in majoritatea programelor software pentru testarea omogenitatii variantelor.
2.4 Teste statistice utilizate pentru verificarea ipotezelor privind mediile a doua grupuri sub SPSS
Primul pas in efectuarea unui test statistic pentru compararea mediilor a doua grupuri il reprezinta alegerea optiunii potrivite in functie de modul in care au fost selectate esantioanele.
A) Esantioane independente
Daca avem doua esantioane independente vom urma urmatoarea cale: Analyze/Compare Means/Independent-Samples T Test (figura nr. 7).
Figura 7. Alegerea testului pentru compararea mediilor a doua esantioane
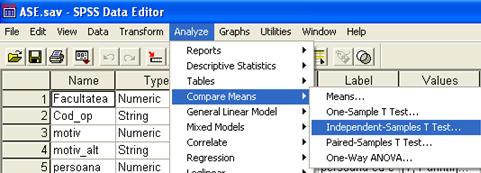
Odata ales testul se intra in fereastra de definire a acestuia (figura 8). Se va trece la Test Variables numele uneia sau mai multor caracteristici pentru care dorim sa efectuam testul. Pentru Grouping Variable se va alege variabila independenta, considerata factor a carui influenta asupra variabilelor independente selectate dorim sa o testam. Deoarece efectuarea acestui test presupune existenta a doar doua grupuri acestea trebuie definite. In exemplul din figura nr. 8 variabila "sexul" imparte esantionul in doua subesantioane independente (1-masculin si 2-feminin).
In situatia in care variabila factoriala imparte esantionul in mai mult de doua grupuri (de exemplu "studii": 1-primare, 2-medii, 3-superioare) este necesar ca in momentul in care definim grupurile trebuie sa alegem doar doua din cele trei categorii sau sa definim o noua variabila "studii superioare" (1-Da, 2-Nu) urmand calea: Transform/Recode/Into Different/Variables.
Figura nr. 8 Definirea testului Independent-Samples T Test
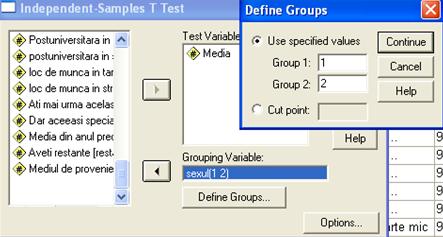
Figura 9 Fereastra de definire a unei noi variabile prin comanda Recode
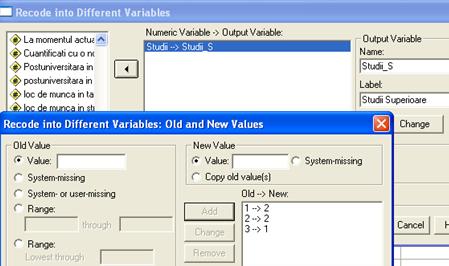
Procedura de definire a variabilei este reliefata prin figura nr. 9. Odata atribuit noul nume al variabilei si eticheta acesteia (optional) se defineste modul in care se transforma vechile valori in cele noi. Avem posibilitatea fie sa atribuim o valoare noua fiecarei valori initiale fie sa atribuim o valoare noua pentru un interval de valori vechi utilizand optiunile Range.
Aceasta noua variabila va constitui factorul de delimitare a celor doua grupuri pentru a realiza Independent-Samples T Test.
In urma procesarii testului definit in fereastra 8 se obtin tabelele 4 si 5.
In tabelul 3 avem afisati ca si in cazul testului One-Sample T test, indicatori de statistica descriptiva precum eroarea medie de reprezentativitate.
Tabel 3
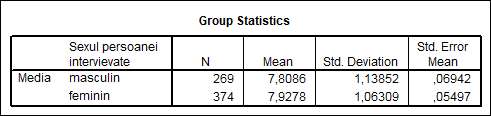
Verificarea ipotezelor privind mediile celor doua grupuri se face pe baza rezultatelor afisate in tabelul 4. Dupa cum s-a precizat in partea teoretica, inainte de procesare trebuie efectuat un test pentru verificarea egalitatii dispersiilor (variantelor). Pentru aceasta programul SPSS utilizeaza testul Levene.
Valoarea calculata a statisticii testului este F=1,16. Daca nivelul de semnificatie este mare (uzual se compara cu 0,05 pentru a garanta rezultatele cu o probabilitate de 0,95) se accepta ipoteza egalitatii dispersiilor si se interpreteaza rezultatele de pe primul rand al tabelului. Valoarea calculata a testului se face pe baza relatiei 5.
In situatia in care valoare nivelului de semnificatie este 0,05 sau mai mic se respinge ipoteza egalitatii dispersiilor se vor interpreta rezultatele de pe a doua linie a tabelului. Valoarea calculata a testului se face de data aceasta pe baza relatiei
In ambele situatii decizia asupra ipotezelor cu privire la mediile celor doua grupuri se ia in functie de valoarea t. Daca testul efectuat este bilateral putem lua decizia si pornind de la nivelul de semnificatie. Valoarea din outputul SPSS se compara cu 0,05 (corespunzatoare unei probabilitati de 0,95). Daca este mai mare se accepta ipoteza diferentei nule iar in caz contrar se accepta alternativa.
Tabel 4
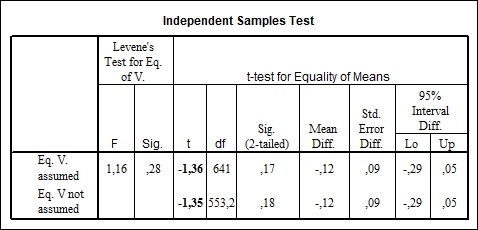
Pentru ca rezultatele testului sa fie concludente este foarte important sa se verifice daca variabilele sunt normal distribuite in special daca esantioanele sunt de volum redus. In acest caz se va recurge la verificarea ipotezelor prin teste neparametrice.
B) Esantioane Dependente
In cazul in care esantioanele sunt dependente din fereastra prezentata in figura nr. 7 se va alege Paired-Samples T Test. Dupa alegerea testului se intra in fereastra de definire a acestuia (figura nr. 10).
Figura nr. 10 Fereastra de definire pentru Paired-Samples T Test
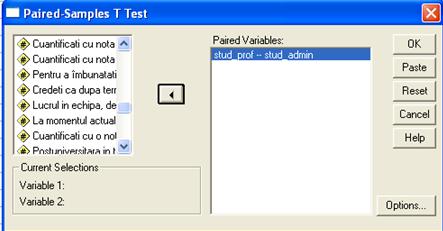
Din lista de variabile se vor forma perechi pentru care urmeaza sa se testeze diferenta dintre medii. In urma procesarii testului se obtin urmatoarele trei tabele:
Ca si in cazul testelor anterioare primul tabel cu rezultate prezinta statistici descriptive pentru variabilele pereche testate precum si eroarea de reprezentativitate.
Tabelul nr. 5.
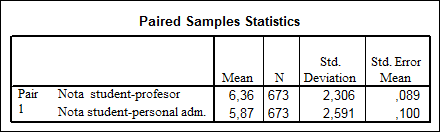
Al doilea tabel (nr. 6) prezinta valoarea coeficientului de corelatie Pearson dintre variabilele pereche precum si nivelul semnificatie al acestuia. O legatura de intensitate puternica sugereaza
In exemplul nostru valoarea obtinuta pentru acesta de 0,338 sugereaza o legatura slaba dar semnificativa din punct de vedere statistic (a
Tabel nr. 6

Informatiile necesare pentru interpretarea testului si luarea deciziei cu privire la ipoteza formulata se gasesc in tabelul nr. 7.
Semnificatia valorilor procesate este:
Mean. Reprezinta media variabilei di=x1i-x2i (paragraful 2.2.);
Standard Deviation. Abaterea mediei patratice a variabilei di=x1i-x2i;
Standad Error Mean. Eroarea de reprezentativitate a variabilei di=x1i-x2i;
95% Confidence Interval of the Difference. Intervalul de incredere pentru media variabilei di;
t Valoarea calculata a testului conform relatiei 6.;
df. Numarul de grade de libertate;
Sig. (2-tailed). Nivelul de semnificatie pentru testul bilateral.
Tabel nr. 7
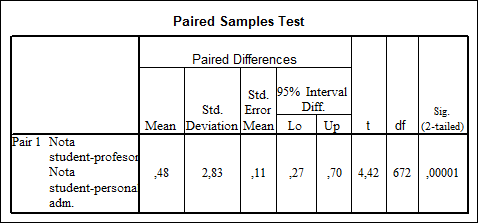
Daca valoarea a este mica (uzual se considera 0,05) consideram ca se respinge ipoteza diferentei nule intre mediile variabilelor pereche si se accepta alternativa.
In exemplul nostru a=0,00001 ceea ce indica faptul ca nivelul de apreciere a relatiei student-proferor difera semnificativ de aprecierea relatiei student-personal administrativ. Probabilitatea cu care este respinsa ipoteza diferentei nule este 0,00009.
2.5 Aplicatii pentru verificarea ipotezelor privind mediile a doua grupuri
Aplicatia 1
In judetul Prahova[4] s-a realizat un sondaj ce a avut drept obiectiv analizarea modului de petrecere a timpului liber. In urma prelucrarii s-au obtinut datele din tabelul 7.
Tabel 7
|
Mediul |
Numar persoane intervievate (pers.) |
Numarul mediu de ore petrecute pe zi la televizor (h/zi) |
Variatia numarului de ore petrecute pe zi la televizor |
|
Urban | |||
|
Rural |
Se cere sa se precizeze daca exista diferente semnificative intre numarul mediu de ore petrecute la televizor pe medii de rezidenta.
Rezolvare
Premizele in care de face testatrea ipotezei sunt:
Esantioanele sunt selectate aleator;
variabila este numerica;
esantioanele sunt de volum mare.
dispersiile in populatie sunt necunoscute substituite cu estimatorii acestora.
Se impune verificarea ipotezei egalitatii dispersiilor pentru a alege testul statistic corespunzator. Deoarece avem doar doua grupuri vom utiliza testul F.
![]() ;
;
Alegem nivelului de semnificatie a=0.01. Deoarece efectuam un test bilateral ne vom uita in Anexa distributiei F la nivelul de semnificatie a
![]()
Alegem nivelului de semnificatie a=0,02. Deoarece efectuam un test bilateral acesta corespunde unui nivel de semnificatie 0,01.
v1=(nU-1)=629; v2=(nR-1)=469
![]() =1
=1
![]() se respinge
se respinge ![]() ; Deci
; Deci ![]() .
.
In aceste conditii pentru a compara numarul mediu de ore petrecute pe zi la calculator pe medii de rezidenta vom utiliza testul z.
Ipotezele sunt:
H0:
![]() =
=![]() si H1:
si H1: ![]() ≠
≠![]()
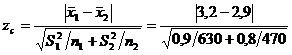 =2,05
=2,05
Valoarea teoretica pentru un nivel de semnificatie a=0,05 este 1,96.
Deoarece ![]() >1,96 se respinge H0.
>1,96 se respinge H0.
Putem afirma cu o probabilitate de 0,95 ca numarul de ore petrecute la televizor difera pe medii de rezidenta.
Aplicatia 2
O firma ce are ca obiect de activitate recrutarea de personal a facut un sondaj in randul candidatilor.
In urma prelucrarii raspunsurilor la intrebarea: "Care este salariul minim net asteptat" s-au obtinut datele din tabelul 8.
Tabel 8
|
Mediul |
Numar persoane intervievate (pers.) |
Salariul mediu asteptat (mii RON) |
Variatia salariului mediu asteptat |
|
Masculin | |||
|
Feminin |
La o prima analiza a datelor observam ca persoanele de sex masculin au asteptari mai mari in ceea ce priveste salariul decat cele de sex .
Se cere sa se verifice aceasta ipoteza pentru o probabilitate de 95%.
Rezolvare
Premizele in care de face testatrea ipotezei sunt:
Esantioanele sunt selectate aleator;
variabila este numerica;
esantioanele sunt de volum mare.
dispersiile in populatie sunt necunoscute substituite cu estimatorii acestora.
Se impune verificarea ipotezei egalitatii dispersiilor pentru a alege testul statistic corespunzator. Deoarece avem doar doua grupuri vom utiliza testul F.
![]() ;
;
![]()
Alegem nivelului de semnificatie a
Deoarece efectuam un test bilateral acesta corespunde unui nivelul de semnificatie 0,025.
v1=(nU-1)=55; v2=(nR-1)=47
![]() =2,2
=2,2
![]() se accepta
se accepta ![]() ; Deci
; Deci ![]() .
.
In aceste conditii vom utiliza testul Student.
Ipotezele testului unilateral dreapta sunt:
H0: ![]() ≤
≤![]() si H1:
si H1: ![]() >
>![]()
Daca valoarea calculata tc este mai mare decat valoarea tabelata corespunzatoare nivelului de semnificatie se respinge ipoteza nula si se accepta ipoteza alternativa.
df=n1+n2-2=104-2=102 iar tdf,a
Statistica testului
este: 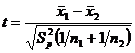
unde ![]() =variatia comuna estimata pe baza dispersiilor
selectiilor si se calculeaza pe baza relatiei.
=variatia comuna estimata pe baza dispersiilor
selectiilor si se calculeaza pe baza relatiei.
![]() =0,627
=0,627
![]() =1,525
=1,525
tc< tdf,a Deci se accepta ipoteza diferentei nule ceea ce inseamna ca nu putem afirma ca pretentiile salariale ale barbatilor sunt semnificativ statistic mai mari decat ale femeilor.
Aplicatia 3
In randul societatilor comerciale din domeniul de activitate "Hoteluri si restaurante" se realizeaza o ancheta periodica ce are la baza un esantion de tip panel. Una din variabilele din planul de observare este "numarul de salariati iar datele din doua anchete succesive sunt prezentate in tabelul 9.
Se cere sa se precizeze daca exista diferente semnificative statistic intre numarul mediu e salariati pe unitate comerciala intre cele doua momente de timp.
Tabel 9
|
societate comerciala |
Numar salariati (pers.) |
societate comerciala |
Numar salariati (pers.) |
||
|
la momentul realizarii panelului |
la momentul verificarii eficientei panelului |
la momentul realizarii panelului |
la momentul verificarii eficientei panelului |
||
|
Yi1 |
Yi2 | ||||
Premizele pentru efectuarea testului pentru observatii perechi sunt:
esantioanele au fost selectate aleator;
esantioanele sunt dependente;
variabilele sunt masurate pe scala interval sau proportionala;
variabila tuturor diferentelor Di=X1i-X2i urmeaza o distributie normala. Conditie necesara in cazul esantioanelor e volum redus.
Primele trei conditii sunt satisfacute. Deoarece esantioanele sunt de volum redus trebuie verificata ipoteza normalitatii distributiei diferentelor. Neavand informatii cu privire la variabila Di se va verifica normalitatea variabilei di.
Pentru aceasta utilizam testul Kolmogorov-Smirnov sub SPSS (verificarea normalitatii distributiilor va fi prezentata in capitolul XXX). In tabelul 10 sunt prezentate rezultatele efectuarii testului. Valoarea mare a nivelului de semnificatie a=0,553 ne indica faptul ca valorile variabilei di urmeaza o distributie normala.
Ipotezele testului sunt:
H0:
![]() ; H1:
; H1: ![]()
Consideram
variabila ![]() ce masoara
diferentele individuale, pentru care calculam media si abaterea
medie patratica (vezi tabelul 11).
ce masoara
diferentele individuale, pentru care calculam media si abaterea
medie patratica (vezi tabelul 11).
Tabelul 10

![]()
Statistica
testului este: 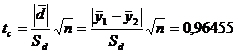
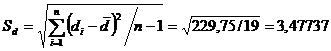
Tabelul 11
|
societate comerciala |
yi1 |
yi2 |
di |
|
|
Total |
Valoarea calculata a testului se compara cu cea teoretica corespunzatoare nivelului de semnificatie ales si n-1=19 grade de libertate. Valoarea teoretica ce corespunde nivelului de semnificatie α=0,05 si numarului de grade de libertate 19 este t=2,09 Deoarece valoarea calculata este mai mica decat cea teoretica se accepta ipoteza diferentei nule ceea ce inseamna numarul mediu de angajati pe unitate comerciala nu s-a modificat semnificativ.
Aplicatia 4
In randul firmelor participante la targul Expo Construct s-a realizat un sondaj ce a avut ca obiectiv Analiza deficitului de forta de munca in constructii. Analizand datele din tabelul 12 se observa ca numarul mediu de angajati al firmelor care resimt o criza a fortei de munca este mai mare decat cel al firmelor care nu au aceasta problema.
Tabelul 12
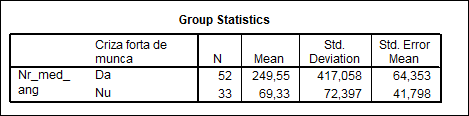
Se cere sa se interpreteze datele din tabelul 13 si sa se precizeze daca se verifica aceasta ipoteza.
Tabelul 13
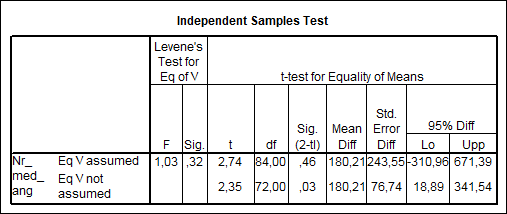
Rezolvare
Premizele in care de face testatrea ipotezei sunt:
Esantioanele sunt selectate aleator;
Variabila este numerica;
Esantioanele sunt de volum mare.
Dispersiile in
populatie sunt necunoscute
substituite cu estimatorii acestora iar ![]() .( Valoarea nivelului de semnificatie a=0,32 indica faptul ca
se accepta ipoteza egalitatii dispersiilor). In
consecinta pentru interpretarea rezultatelor vom lua din tabel datele
de pe primul rand al acestuia.
.( Valoarea nivelului de semnificatie a=0,32 indica faptul ca
se accepta ipoteza egalitatii dispersiilor). In
consecinta pentru interpretarea rezultatelor vom lua din tabel datele
de pe primul rand al acestuia.
Ipotezele testului unilateral dreapta sunt:
H0: ![]() ≤
≤![]() si H1:
si H1: ![]() >
>![]()
df=n1+n2-2=84
tdf,a
![]() 2,74
2,74
tc> tdf,a
Deci se respinge ipoteza diferentei nule (cu o probabilitate de 0,95) ceea ce inseamna ca societatile care resimt deficitul de forta de munca au un numar mai mare de angajati decat cele care nu au aceasta problema.
Aplicatia 5
S-a realizat o ancheta asupra fortei de munca din sectorul energetic Bucuresti pe baza unui sondaj statistic efectuat in trei societati comerciale, cu activitati de baza diferite din acest domeniu. Una din intrebarile din chestionar a fost urmatoarea:
Q11. Acordati o nota de la 0-10 pentru importanta acordata in firma fiecarui criteriu ce determina politica salariala.
|
Criteriul |
Politica salariala |
|
1. Nivelul calificarii | |
|
2. Vechimea in munca | |
|
Relatiile personale |
Rezolvare
Prin aceasta intrebare am intentionat sa observam cum percep salariatii importanta acordata de conducerea societatii nivelului de calificare (R1), a vechimii in munca (R2) si a relatiilor personale (R3) in politica de salarizare. Rezultatele obtinute in urma prelucrarii pentru una din societatile analizate sunt prezentate in tabelul 14.
Tabel nr. 14
|
Nivelul calificarii (R1) Scor mediu |
Vechimea in munca (R2) Scor mediu |
Relatiile personale (R3) Scor mediu |
|
|
|
|
Pentru a stabili o ierarhie a importantei criteriilor in cadrul fiecarei societati trebuie testata semnificatia diferentei dintre punctajul mediu obtinut de fiecare criteriu in parte. Fiind vorba de observatii perechi am utilizat testul Student pentru esantioane dependente. In urma efectuarii testului s-au obtinut rezultatele din tabelul 15.
Pentru comparatia punctajelor obtinute de criteriul R1 si R2 valoarea testului Student pentru observatii perechi este -5. Efectuand un test unilateral stanga ipotezele sunt:
H0:
![]()
![]() si H1:
si H1: ![]() <
<![]() Valoarea teoretica corespunzatoare unei probabilitati de 95% de garantare a
rezultatelor este tdf=116-1,a= -1,645. Valoarea calculata de -5 este mai mica decat cea
teoretica ce duce la acceptarea
ipotezei alternative.
Valoarea teoretica corespunzatoare unei probabilitati de 95% de garantare a
rezultatelor este tdf=116-1,a= -1,645. Valoarea calculata de -5 este mai mica decat cea
teoretica ce duce la acceptarea
ipotezei alternative.
Tabel nr. 15

In
mod similar am efectuat un test unilateral dreapta pentru
compararea criteriilor R2 si R Ipotezele sunt: H0:
![]()
![]() si H1:
si H1: ![]() >
>![]() Valoarea teoretica corespunzatoare unei probabilitati de 95% de garantare a
rezultatelor este tdf=116-1,a=1,645 cea ce duce la acceptarea ipotezei alternative.
Valoarea teoretica corespunzatoare unei probabilitati de 95% de garantare a
rezultatelor este tdf=116-1,a=1,645 cea ce duce la acceptarea ipotezei alternative.
Din compararea punctajelor pentru criteriile R1 si R3 prin efectuarea unui test bilateral reiese ca nu exista diferente semnificative.
In finalul acestei analize se poate afirma cu o probabilitate de 95% ca cel mai important criteriu al politicii de salarizare la societatea comerciala analizata este vechimea in munca, intre celelalte doua criterii neputandu-se stabili o ierarhie. Relatia dintre cele trei criterii la SC1 este:
|
Nivelul calificarii |
< |
Vechimea in munca |
|
Relatiile personale |
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 5002
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2026 . All rights reserved