Determinarea zonelor de influenta ale localitatilor cu rol de loc central. Spatiul geografic functional

Numarul de ore alocat: 4

1. Introducere. Metoda poligoanelor lui Thiessen

Christaller, in teoria locurilor centrale, a propus o determinare de natura geometrica a zonelor de influenta a localitatilor cu rol de loc central. Astfel, la modul ideal, conform teoriei amintite, zona de influenta a fiecarui loc central ar fi un hexagon. In realitate, chiar si acolo unde se intrunesc o parte din ipotezele de la care pleaca teoria, locurile centrale nu au o dispozitie geometrica in spatiu, iar zonele lor de influenta au forme variate si dimensiuni diverse.

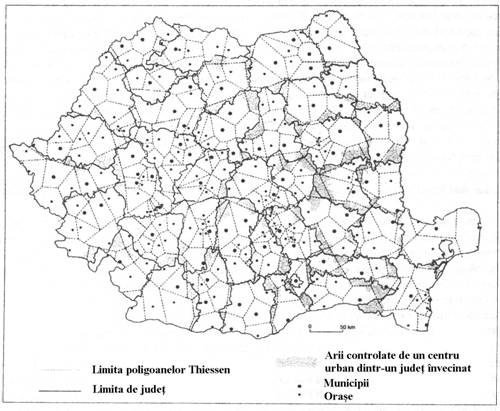
Fig. 23. Zonele de influenta teoretica ale centrelor urbane romanesti, determinate prin metoda poligoanelor lui Thiessen. Sursa: O. Groza (2002)

Cea mai simpla metoda de a determina, pe cale matematica (geometrica), zonele de influenta ale unei retele de locuri centrale intr-un spatiu dat, este cea a poligoanelor lui Thiessen. Astfel, indiferent de modul de dispunere in spatiu a locurilor centrale, ea statueaza ca fiecare client va apela la locul central cel mai apropiat ca distanta. Nu se tine cont de o posibila ierarhie a locurilor centrale, ci toate sunt considerate de acelasi rang. Astfel, rezulta zone de influenta de forma unor poligoane. Aceste limite ale zonelor de influenta se mai numesc si teoretice. Analizati zonele de influenta teoretice ale oraselor romanesti in anul 2000 (O. Groza, 2002). Ce constatati? . .

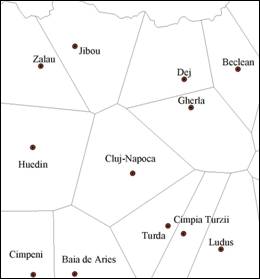
Fig. 24. Determinarea zonei de influenta a orasului Cluj-Napoca prin metoda poligoanelor lui Thiessen. Sursa: autorul

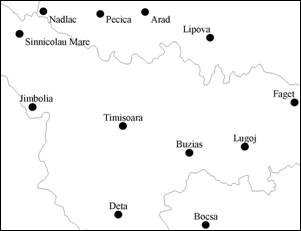
Fig. 25. Municipiul Timisoara si centrele urbane invecinate. Determinati zona de influenta teoretica a Timisoarei prin metoda poligoanelor lui Thiessen. Sursa: autorul

Aceste limite ale zonelor de influenta teoretice (poligoanele lui Thiessen) se pot trasa cu ajutorul calculatorului, dar si manual. Modalitatea grafica de a obtine zona de influenta a municipiului Cluj-Napoca este urmatoarea:

a)      Se uneste punctul reprezentand municipiul Cluj-Napoca cu toate punctele reprezentand orasele inconjuratoare;

b)      Cu ajutorul unei rigle, se puncteaza mijlocul fiecarui segment de dreapta;

c)      Cu un echer, se traseaza cate o dreapta prin fiecare din punctele stabilite, astfel incat acestea sa fie perpendiculare pe segmentele de dreapta initiale;

d)      Dreptele astfel rezultate se intersecteaza, rezultand un poligon, ce reprezinta zona teoretica de influenta a municipiului Cluj-Napoca.

Problema. Stabiliti care este zona de influenta teoretica a municipiului Timisoara, urmand metoda descrisa mai sus.

2. Teoria atractiei urbane si modelul gravitational Reilly-Converse

Este evident ca metoda descrisa mai sus este simplista si nu poate genera rezultate valide, astfel incat ea mai este folosita doar pentru a compara zonele de influenta teoretice cu cele reale.

Inca din 1929, anterior deci teoriei locurilor centrale, geograful american W.J. Reilly a incercat sa stabileasca o analogie intre modul de atractie comerciala a doua orase si legea atractiei universale a lui Newton. Aceasta a fost formulata in felul urmator: doua orase atrag cumparatori din regiunea rurala inconjuratoare in mod direct proportional cu populatia lor si invers proportional cu patratul distantei dintre ele.

Presupunem ca exista doua orase, A si B, a caror populatie este egala cu P_A si P_B, iar intre ele o localitate H, aflata la distanta D_A de orasul A, respectiv D_B de orasul B. Ponderea celor care prefera sa mearga la cumparaturi in A este C_A, iar ponderea celor care merg in orasul B, C_B. Atunci, conform celor enuntate mai sus:

Conform acestei formulari matematice, influenta unui oras asupra spatiului inconjurator descreste cu distanta si creste cu marimea orasului.

Aceasta formulare a fost utilizata de P.D. Converse in 1935, care a adaugat teoriei lui Reilly o idee interesanta, si anume existenta unui punct de frontiera intre cele doua orase considerate, A si B. Dupa Converse, exista un punct intermediar C, pe dreapta AB, unde volumul cumparaturilor efectuate in cele doua orase, este egal. Rezulta ca .

De aici, se poate calcula distanta la care se situeaza acest punct intermediar fata de orasul A, respectiv fata de orasul B.

Daca 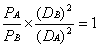, atunci 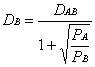iar D_A = D_AB - D_B

Problema. Demonstrati validitatea formulei de mai sus, plecand de la formula initiala a lui Reilly si asumptia lui Converse.

Punctul "de frontiera" marcheaza asadar limita zonei de influenta a celor doua orase. Un exemplu este oferit de V. Surd (2003), pentru calcularea punctului "de frontiera" (sau de atractie zero) dintre municipiile Cluj-Napoca si Turda. Astfel, daca se rotunjesc datele referitoare la populatie si distanta (Cluj-Napoca 360 000 de locuitori, Turda 60 000, distanta = 30 km), rezulta ca punctul de atractie zero este situat la 8,5 km de Turda si 21,5 km de Cluj-Napoca, ceea ce corespunde in linii mari cu realitatea.

Inlocuiti datele in formula pentru a obtine singuri rezultatul.

Acum incercati sa obtineti distanta la care se situeaza punctul de atractie zero dintre muncipiul Cluj-Napoca si urmatoarele centre urbane inconjuratoare: Bistrita, Beclean, Dej, Gherla, Jibou, Zalau, Huedin, Campeni, Baia de Aries, Campia Turzii, Sarmasu, Targu Mures.

Pentru a obtine (la modul simplist) zona de influenta a municipiului Cluj-Napoca, se procedeaza ca si in cazul poligoanelor lui Thiessen, doar ca perpendicularele pe segmentele de dreapta ce unesc municipiul Cluj-Napoca de centrele urbane inconjuratoare se traseaza din punctul de atractie zero stabilit pe fiecare segment de dreapta. Trebuie mentionat ca, in realitate, zonele de influenta au limite mai degraba curbe pentru centrele mici. Ce constatati, comparativ cu zona de influenta calculata prin metoda poligoanelor lui Thiessen?. .

Unul dintre minusurile teoriei este si acela ca nu se tine cont de eventuala prezenta a unor discontinuitati geografice intre orase, spatiul este considerat omogen (izotrop), ca in majoritatea teoriilor spatiale. Rezultate mai adecvate se obtin daca, in locul distantei in linie dreapta intre orase, se foloseste distanta reala de-a lungul cailor de comunicatie principale (in mod firesc, caile rutiere).

Recalculati zona de influenta a municipiului Cluj-Napoca pornind de la valorile distantei reale intre acesta si centrele urbane amintite mai sus. Ce impediment apare? Cum se poate rezolva?. .

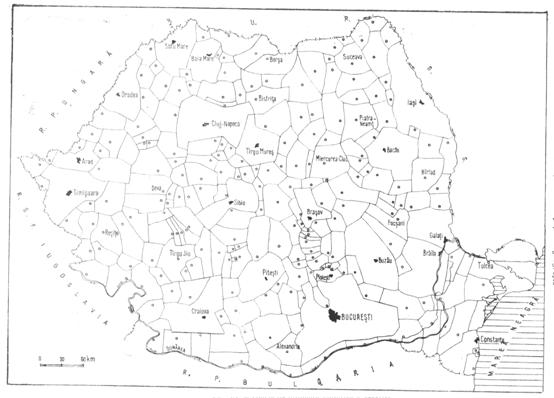
Fig. 26. Zonele de influenta teoretica ale centrelor urbane din Romania calculate pe baza formulei Reilly-Converse. Sursa: I. Ianos (1987)

I. Ianos (1987) a realizat o harta cu aria teoretica de influenta a oraselor Romaniei, pe baza formulei Reilly-Converse. Va rog sa remarcati principalele diferente fata de harta zonelor de influenta calculate pe baza poligoanelor lui Thiessen:

Rezultatele au capacitate redusa de generalizare. Cu toate contestatiile la care a fost supusa, teoria atractiei urbane fundamentata de Reilly continua sa atraga cercetatori. Ea a fost dezvoltata in anii 50 si 60 de Huff, iar in anii 80 de Wilson, ajungandu-se la formule mai complicate, care iau in considerare mai multe variabile, precum atractivitatea zonelor de destinatie, eliminarea viziunii simpliste asupra distantei, complementaritatea etc. (I. Ianos, J.B. Humeau, 2000).

3. Metode analitice de determinare a zonei de influenta

Metoda punctelor pleaca de la ipoteza ca se cunoaste domiciliul (provenienta) tuturor celor care se deplaseaza intr-o localitate cu rol de loc central, indiferent de motivatia acestei calatorii, si nu se afla doar in tranzit. Astfel, fiecare persoana este reprezentata printr-un punct corespunzator domiciliului sau stabil. Rezulta o harta a punctelor, care in mod normal reprezinta asezarile situate in zona de influenta a locului central analizat. Desigur, unele persoane provin din zone mai indepartate, dar acestea reprezinta o pondere neinsemnata (maxim 5%), reprezentand mai degraba vizite ocazionale, si nu cele frecvente.

Aceasta metoda nu tine cont de posibilele variatii ale densitatii populatiei in spatiul pe care il reprezinta zona de influenta a orasului; astfel, localitatile mari apar pe harta ca fiind mai bine reprezentate ca numar de clienti in comparatie cu asezarile mici, chiar daca ponderea clientilor apartinand acestora din urma ar fi, de fapt, mai ridicata.

Pentru a realiza aceasta harta, se aplica un chestionar asupra clientilor unei zone comerciale importante, astfel incat esantionul sa fie reprezentativ. In esantion se pot include si elevii ce studiaza la liceele din locul central amintit, sau studentii (daca este cazul unui centru universitar), pe baza informatiilor obtinute de la institutii. De asemenea, semnificativa ar fi si introducerea in baza de date a bolnavilor din spital(e).

Harta astfel obtinuta ofera informatii utile in primul rand pentru comerciantii si reprezentantii institutiilor din locul central, care pot sa stabileasca, in functie de aceasta, o strategie de atragere a clientilor (de exemplu, prin mijloace publicitare).

Metoda ponderilor este in masura sa dea rezultate mai exacte, intrucat are in vedere nu cifre absolute ale clientilor, ci ponderea acestora din total. Astfel, pentru aplicarea acestei metode, este necesara deplasarea in fiecare din asezarile care ar putea face parte din zona de influenta a unui loc central. Se aplica, de asemenea, metoda chestionarului, de data aceasta pentru a interoga potentialii clienti asupra destinatiei lor favorite, precum si a frecventei de vizitare a fiecarui loc central pe care acestia il mentioneaza. In acest mod, ne putem edifica si asupra impactului concurentei asupra unui loc central, si a limitei zonei sale de influenta. Se calculeaza, pentru fiecare asezare in parte, pe baza unui esantion reprezentativ, ponderea deplasarilor spre locul central analizat.

Pe baza studiilor empirice ce au avut la baza aceste metode, s-a constatat ca zonele de influenta pot fi la randul lor divizate, astfel:

zona de influenta apropiata (primara sau Umland) concentreaza 70-80% din deplasarile in locul central considerat, majoritatea locuitorilor fiind clienti regulati;

zona de influenta departata (secundara sau Hinterland), in care relatia cu locul central este mai putin intensa (15-25% din "vizite"), majoritatea locuitorilor se deplaseaza doar ocazional in asezarea supusa analizei;

zona de influenta tertiara este foarte extinsa si se caracterizeaza prin deplasari exceptionale, foarte rare, ale locuitorilor sai in locul central vizat. Ca urmare a globalizarii tot mai accentuate, anumite orase au o zona de influenta tertiara de marime considerabila.

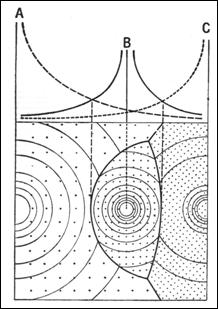
Fig. 27. Zonele de influenta a trei orase invecinate, de marimi distincte. Sursa: Jacqueline Beaujeu-Garnier, G. Chabot (1971)

Cele trei diviziuni ale zonei de influenta se dispun mai mult sau mai putin concentric in jurul locului central, dar pot avea forme variate, induse de factori fizico-geografici (catene montane, deserturi, lacuri, cursuri de apa), prezenta altor locuri centrale concurente, factori de natura politica (granite de stat, limite de unitati administrative) etc.

Problema. Determinati empiric, pe baza cunostintelor voastre, zona de influenta apropiata, departata si tertiara pentru localitatea cu rol de loc central pe care o cunoasteti cel mai bine. Aduceti argumente in favoarea delimitarilor efectuate.

4. Spatiul geografic functional

Spatiul geografic functional este conceput ca un spatiu in care asezarile formeaza un ansamblu clar ierahizat (I. Ianos, 1987). Interactiunile care au loc intr-o astfel de entitate teritoriala sunt orientate (polarizate) de locuri centrale de diferite ranguri. In acest cadru, sistemul de asezari trebuie privit ca un tot unitar, care inglobeaza relatiile dintre fiecare asezare cu teritoriul sau adiacent. Prin urmare, spatiul geografic functional se compune din reuniunea integrala a spatiilor de influenta ale tuturor asezarilor ce il compun (I. Ianos, op. cit.). In conformitate cu aceasta definitie, in functie de pozitia pe care o ocupa asezarea coordonatoare (locul central de rang superior) in ierarhia nationala, se poate defini subunitatea corespunzatoare. In acest mod, se poate delimita concret fiecare spatiu geografic functional, precizandu-se si rangul pe care il detine asezarea coordonatoare.

Structura majora a spatiului geografic functional este urmatoarea: componente (asezarile), mediu (cuprinzand spatiul din afara vetrei asezarilor) si relatii (intre componente si mediu, precum si intre subansamblurile lor). Spatiul geografic functional se caracterizeaza printr-o serie de trasaturi distincte:

polaritatea: orice portiune dintr-un teritoriu, chiar si nelocuit, influenteaza (prin potentialul sau economic) sau/si se afla sub influenta mai accentuata sau mai difuza a unei asezari;

integrarea in ansamblul national: spatiul geografic functional nu este un sistem inchis, ci are legaturi si relatii de diverse naturi cu spatiile geografice functionale limitrofe, integrandu-se in spatiul geografic national;

unicitatea: nu exista spatii geografice functionale identice;

integrarea functionala: excedentele locale de materie si energie se insumeaza si completeaza deficitele existente la nivele superioare ale ierarhiei de asezari, si invers, excedentele de informatii sau de produse prelucrate si servicii specializate de la nivelele superioare vin sa completeze deficitele de la nivelele inferioare;

dinamsimul: limitele unui spatiu geografic functional pot sa varieze in timp, prin procese de restrangere sau de extindere, in functia de dinamica centrului coordonator si a celorlalte asezari cu rol de loc central pe care le cuprinde.

Pentru I. Ianos (1987), spatiul geografic functional este unitatea de baza in organizarea spatiului geografic.

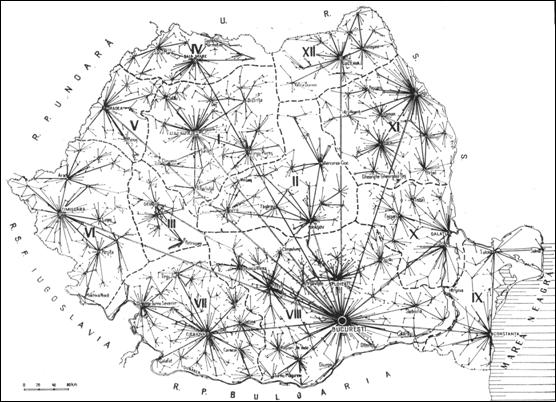
Fig. 28. Spatiul geografic functional al Romaniei. Principalele centre coordonatoare si regiuni polarizate de acestea. Sursa: I. Ianos (1987)

Acelasi autor, intr-o lucrare mult mai recenta (I. Ianos, J.B. Humeau, 2000), evita insa sa foloseasca conceptul de spatiu geografic functional, si utilizeaza doar pe acela, mult mai larg, de sistem de asezari.

Sunt delimitate urmatoarele tipuri morfologice de sisteme de asezari (spatii geografice functionale):

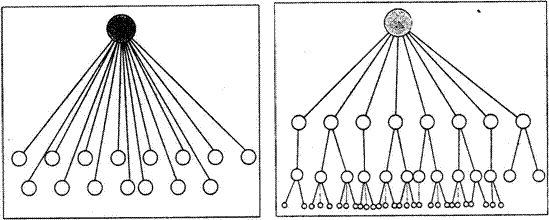
sisteme de asezari excesiv monocentrice;

sisteme de asezari monocentrice;

sisteme de asezari monocentrice echilibrate;

sisteme de asezari bicentrice;

sisteme de asezari policentrice.

In raport cu nivelul de dezvoltare al fiecarei tari, se poate observa ca rolul de asezare coordonatoare la nivelul regional il poate avea o metropola regionala, un oras mare, sau chiar un oras mijlociu, cu functii de loc central importante.

Fig. 29. Stanga: sisteme de asezari excesiv monocentrice. Dreapta: sisteme de asezari monocentrice. Sursa: I. Ianos, J.B. Humeau (2000)

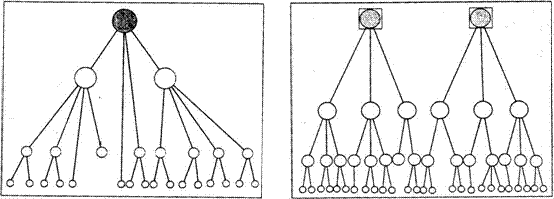
Fig. 30. Stanga: sisteme de asezari monocentrice echilibrate. Dreapta: sisteme de asezari bicentrice. Sursa: I. Ianos, J.B. Humeau (2000)

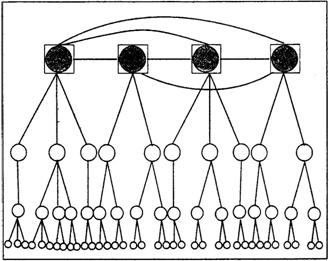
Fig. 31. Sisteme de asezari policentrice. Sursa: I. Ianos, J.B. Humeau (2000)

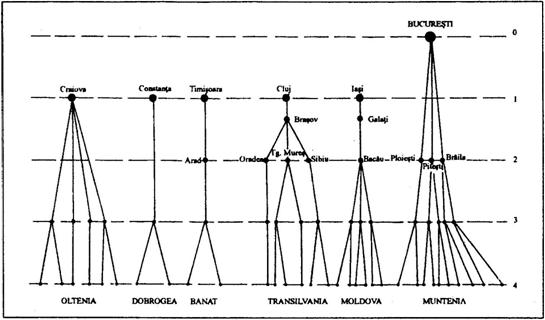
Fig. 32. Ierarhia asezarilor la nivelul superior, pe marile provincii istorice. Sursa: I. Ianos, J.B. Humeau (2000)

Analizati sistemele de asezari din Romania, la nivelul provinciilor istorice. Incadrati fiecare sistem de asezari intr-unul din tipurile de mai sus, precizand asezarea coordonatoare (centrul de comanda) a spatiului geografic functional si asezarile de pe nivelele ierarhice inferioare:

Oltenia:.. ..;

Dobrogea:. ..;

Banat:. ..;

Transilvania:..;

Moldova: ..;

Muntenia:.. ..;

La nivel local, este mult mai dificil de a distinge structuri morfologice de acest tip, indeosebi in spatiile profund rurale (I. Ianos, J.B. Humeau, op. cit.).

5. Studiu de caz: zonele de influenta ale centrelor de comanda din Banat

In tema 4, s-a realizat o ierarhizare a localitatilor cu rol de loc central din Banat. Pe baza cercetarilor intreprinse, s-au delimitat spatiile geografice functionale ale fiecarui loc central, de la rangul 1 (Timisoara, care polarizeaza intreaga regiune) pana la rangul 6. Deci, regiunea corespunde administrativ judetelor Arad, Timis si Caras-Severin, si este conceputa ca un spatiu geografic functional avand Timisoara drept asezare coordonatoare (R. Rusu, 2004).

Principalul centru polarizator al Banatului este Timisoara, singura localitate de rangul 1, a carei arie de atractie la acest nivel depaseste probabil limitele regiunii studiate. Important centru universitar, totodata singurul cu traditie din partea de vest a tarii, este orasul cu cel mai mare aeroport din tara dupa Bucuresti, gazda a numeroase institutii de rang inalt (opera, spitale specializate, curtea de apel, TVR Timisoara, Radio Timisoara), care deservesc intreaga regiune. Daca pana la primul razboi mondial concurenta orasului invecinat, Arad, a fost acerba, in perioada interbelica si mai ales in perioada postbelica, Timisoara s-a afirmat ca metropola acestei regiuni, favorizata si de organizarea administrativa de dupa razboi, pana in 1968, cand a avut rangul de capitala regionala, in vreme ce Aradul a decazut la nivelul de centru de raion.

La nivelul 2, Timisoara pierde in favoarea Aradului judetul omonim, care se subordoneaza, la acest nivel, orasului de pe Mures. Este o intamplare faptul ca Aradul nu a avut aceeasi sansa ca si Timisoara, dezvoltarea sa fiind identica cu a acesteia pana in apropierea celui de-al doilea razboi mondial. Transferul la Timisoara a institutiilor regionale aradene a lasat urme adanci, afectand rangul localitatii. In prezent, Aradul "lupta cu arme" inegale in fata Timisoarei, detinand o serie de institutii in masura a asigura rangul de oras regional: universitate de stat si privata, spitale, teatre, numerosi dealeri auto, un potential de transport ridicat, comparabil cu al vecinilor de pe Bega, magazine specializate precum si super-market-uri (Billa, Profi).

Rangul 3 este cel al resedintelor de judet; aici apare si orasul Resita, care a primit pentru prima data o functie administrativa in anul 1968, cand a fost numit resedinta noului judet Caras-Severin. La acest nivel isi exercita autoritatea o serie de institutii care au o relevanta administrativa: tribunalul, spitalul judetean, prefectura, consiliul judetean, administratia financiara, biblioteca judeteana, precum si altele, obisnuite in cadrul resedintelor de judet: teatru, magazin universal, magazine specializate, dealeri auto. Resita este un oras cu veche traditie industriala, care a avut o dezvoltare deosebita in epoca comunista, dar in prezent se afla intr-un regres evident, si ca urmare a problemelor principalei intreprinderi din oras, Combinatul Metalurgic.

Rangul 4 este reprezentat de orasele mijlocii, foste resedinte de judet: Lugoj si Caransebes, la care se adauga, evident, toate orasele mentionate mai sus cu care acestea intra in concurenta. Se observa ca Aradul ramane cu aceeasi zona de influenta la nivelele 2, 3 si 4, intrucat in judetul Arad nu exista nici o localitate de rang superior nivelului 5. Pe de alta parte, Lugojul preia, la nivelul 4, jumatatea estica a judetului Timis, afectand asadar aria de influenta a Timisoarei, iar Caransebes - jumatatea estica a judetului Caras-Severin, respectiv culoarul Timis-Cerna-Bistra, afectand aria de influenta (destul de fortata) a municipiului Resita. La nivelul oraselor mijlocii, se poate constata prezenta a numeroase institutii regionale: licee cu diferite specializari, universitati sau filiale ale acestora, spitale municipale, teatru (uneori) si cinematografe, magazine generale si specializate, dealeri auto (in special pentru masini produse in Romania - Dacia sau Daewoo), numeroase banci si bancomate, service-uri pentru automobile.

Deosebit de numeroase sunt localitatile situate la nivelul 5: Sannicolau Mare, Bocsa, Oravita, Lipova, Ineu, Sebis, Chisineu Cris, Deta, Faget, Otelu Rosu, Moldova Noua - toate acestea fiind orase mici, la care se adauga si doua localitati rurale de acelasi rang - Bozovici si Gurahont. Este nivelul judecatoriilor si spitalelor, pe baza circumscriptiilor acestora facandu-se si delimitarea ariilor de influenta la acest nivel. Toate localitatile mentionate detin un spital; cateva dintre ele, situate in apropierea unui centru de rang superior sau de rang identic, nu au judecatorie (Otelu Rosu, Bocsa, Sebis). Toate aceste localitati au o zona de influenta de marime medie, compusa dintr-un numar de minim cinci comune, pe care o deservesc prin diverse institutii de caracter regional: licee cu profile diverse, judecatorie, spital (deja mentionate), magazine diverse, dar fara o specializare deosebita, gari (exceptie: Bozovici si Moldova Noua), unele service-uri auto, benzinarii, banci (cel putin una) si bancomate (exceptie: Gurahont).

La baza ierarhiei urbane se afla orasele mici de nivelul 6: Jimbolia, Nadlac, Curtici, Buzias, Recas, Ciacova, Gataia, Baile Herculane, Pancota, Anina, Pecica, Santana, la care se adauga un numar mai mare de localitati rurale de acelasi rang: Savarsin, Mehadia si Beliu. Acestea sunt localitati a caror arie de influenta este destul de redusa, la un numar de maxim cinci comune, din doua cauze fundamentale: imediata apropiere a unui centru urban de rang superior si, respectiv, vecinatatea granitei (Nadlac, Curtici, Jimbolia). Unele dintre ele isi datoreaza statutul urban unor factori precum statutul de localitate in apropierea punctului de trecere frontiera (exact localitatile mentionate) sau cel de statiune balneo-cliamterica (Baile Herculane, Buzias). Comunele amintite se situeaza la acelasi nivel si detin aproximativ aceleasi dotari, cea mai importanta fiind liceul; ariile de influenta ale liceelor au constituit de fapt principalul criteriu de delimitare a zonei de influenta la acest nivel. Lipsesc judecatoriile, spitalele (cu unele exceptii: Gataia, Jimbolia), mai caracteristica fiind prezenta centrelor de sanatate. Bancile apar doar in anumite situatii (Curtici - ca urmare a prezentei zonei libere) sau sunt putin numeroase, maxim doua, din care de obicei una este CEC-ul. Majoritatea au acces la calea ferata. Importanta lor comerciala este redusa, cu unele exceptii (de exemplu, piata de animale din Pancota). Nu detin in mod obisnuit cinematografe in functiune.

Ceea ce iese in evidenta este prezenta competitiei intre orase la toate nivelele; astfel, Timisoara nu are nici un concurent la nivelul 1 (cel putin nu in regiunea analizata), insa are un concurent la nivelul 2 (Arad), doi la nivelul 3 (Arad si Resita), inca doi la urmatorul nivel s.a.m.d, astfel incat la nivelul 6, Timisoara intra in competitie cu orase mici precum Jimbolia, Recas sau Buzias, si chiar localitati rurale precum Ciacova, iar la nivelul 7 intervin si alte localitati rurale, situate in imediata sa apropiere (Carpinis, Ortisoara, Biled).

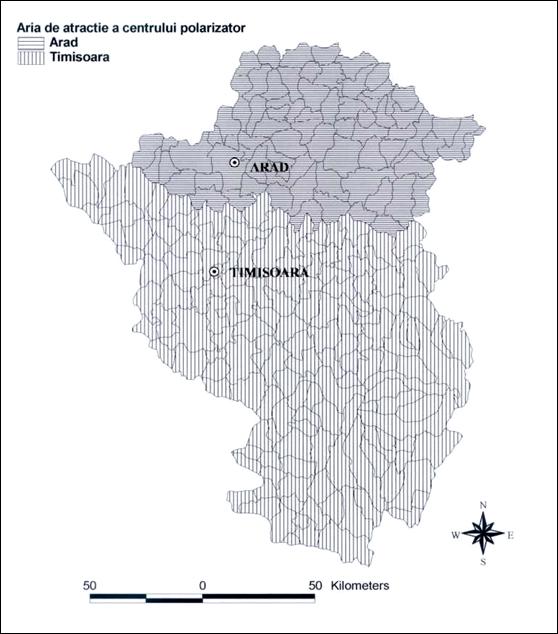
Fig. 33. Aria de atractie a centrelor polarizatoare de rangul 2. Sursa: R. Rusu (2004)

Zonele de influenta nu sunt statice, ele au un carcater dinamic si se pot cu usurinta schimba de la o perioada istorica la alta. Ceea ce am prezentat aici este o analiza sincronica, respectiv situatia asa cum se prezinta ea la momentul actual, in anul 2004. Aceeasi afirmatie se poate face si despre situarea unui oras in ierarhie: pozitia sa se poate schimba in timp, unele tind sa urce, altele sa coboare

6. Problema

Pe baza materialului prezentat, incercati o schema de reprezentare a unui spatiu geografic avand drept asezare coordonatoare localitatea voastra natala. Incercati sa surprindeti ierarhizarea pe ranguri a localitatilor subordonate, si concurenta centrului de comanda cu acestea in cazul institutiilor (dotarilor) de rang inferior.

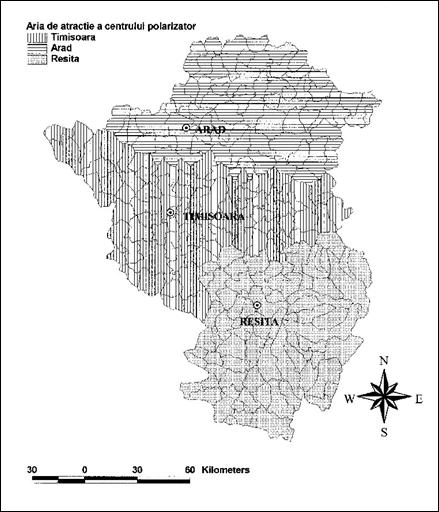
Fig. 34. Aria de atractie a centrelor polarizatoare de rangul 3. Sursa: R. Rusu (2004)

BIBLIOGRAFIE

1. Beaujeu-Garnier, Jacqueline, Chabot, G. (1971), Geografia urbana, Edit. Stiintifica, Bucuresti;
2. Cliquet, G. (1992), Management stratgique des points de vente, Sirrey;
3. Converse, P.D. (1935), Elements of Marketing, Prentice Hall, New York;
4. Grimmeau, J.P. (2003), Localisation des entreprises et gomarketing Presses Universitaires de Bruxelles, Bruxelles;
5. Groza, O. (2002), Polarisation territoriale et organisation administrative en Roumanie. The missing link: le niveau regional, in Ungureanu, Al., Groza, O., Muntele, I. (coord.), Moldova. Populatia, forta de munca si asezarile umane in tranzitie, Edit. Corson, Iasi;
6. Gusti, G. (1974), Forme noi de asezare, Edit. Tehnica, Bucuresti;
7. Huff, D. (1963), A Probabilistic Analysis of Shopping Center Trade Area, Land Economics, 53;
8. Ianos, I. (1987), Orasele si organizarea spatiului geografic, Edit. Academiei RSR, Bucuresti;
9. Ianos, I., Humeau, J.B. (2000), Teoria sistemelor de asezari umane, Edit. Tehnica, Bucuresti;
10. Isard, W. (1956), Location and Space Economy, MIT Press, Cambridge, Mass.;
11. Molnar, E., Maier, A., Cianga, N. (1975), Centre si arii de convergenta din Romania, Studia UBB, Geographia, XX, 2;
12. Reilly, W.J. (1929), Methods for the Study of Retail Relationships, University of Texas Bulletin, 2944;
13. Reilly, W.J. (1931), The Law of Retail Gravitation, Prentice Hall, New York;
14. Rusu, R. (2004), Centrele urbane de comanda din Banat si ariile lor de influenta, Studia UBB, Sociologia, 1, Cluj-Napoca;
15. Schller, P. (1953), Aufgaben und Probleme der Stadtgeographie, Erdkunde;
16. Surd, V. (2003), Geografia asezarilor, Edit. PUC, Cluj-Napoca;
17. Talanga, C. (2000), Transporturile si sistemele de asezari din Romania, Edit. Tehnica, Bucuresti;
18. Ullman, E.L. (1980), Geography as Spatial Interaction, University of Washington Press, Seattle;
19. Ventura, F., Wrneryd, O. (1983), Differentiation of settlement systems on the basis of population densities and level of development, Geographica Polonica, 47;
20. Wilson, A.G. (2000), Complex Spatial Systems: The Modelling Foundations of Urban and Regional Analysis, Pearson Education, Harlow.

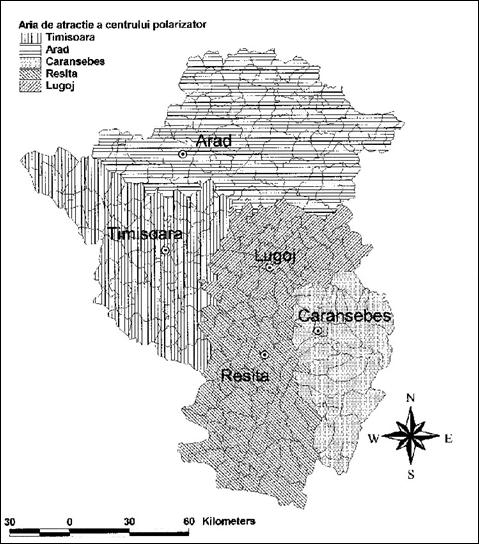
Fig. 35. Aria de atractie a centrelor polarizatoare de rangul 4. Sursa: R. Rusu (2004)

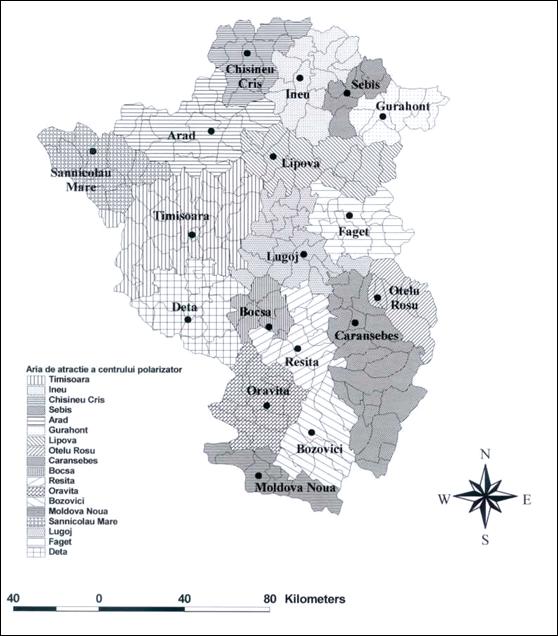
Fig. 36. Aria de atractie a centrelor polarizatoare de rangul 5. Sursa: R. Rusu (2004)

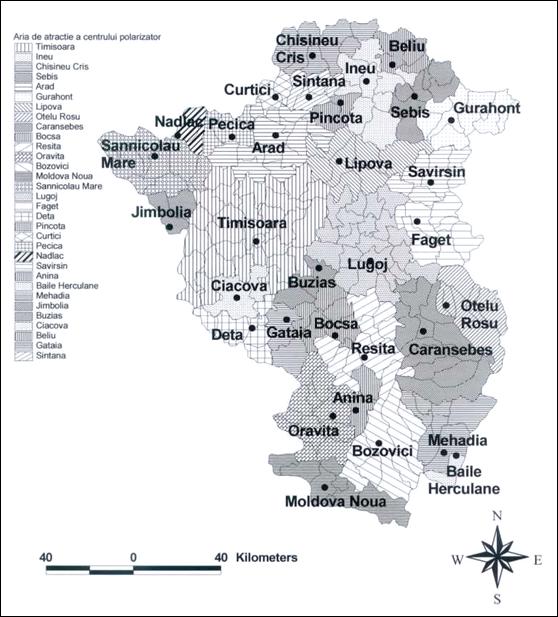
Fig. 37. Aria de atractie a centrelor polarizatoare de rangul 6. Sursa: R. Rusu (2004)