| CATEGORII DOCUMENTE |
| Demografie | Ecologie mediu | Geologie | Hidrologie | Meteorologie |
Analiza stabilitatii schemelor cu Diferente Finite pentru ecuatia cinematica a propagarii undei de viitura
Se considera un sector de rau de lungimea L, avand o albie larga care se poate asimila cu o sectiune transversala dreptunghiulara foarte larga (B>>h).

Adancimea apei in regim permanent si uniform este de h0. Se presupune ca la momentul t0 apare o unda de viitura care se poate aproxima sub o forma triunghiulara.

Schema de calcul al undei de viitura pe un sector de curs de apa
Date initiale:
n = 20
Q = 40 + 20 = 60 m3/s - debitul cursului de apa
B = 30 m - latimea albiei
h0 = 2.00 m - adancimea albiei
Distanta dintre punctele 1,2,3,., 8 este de Δx = 100m.
Ecuatia cu derivate partiale a undei cinematice:
![]()
unde a - viteza de propagare a undei
![]()
vm - viteza apei in rau in regim uniform
![]()
Se va utiliza ecuatia cu diferente finite corespunzatoare schemei explicite regresive:
![]()
Unda de viitura la momentul initial este urmatoarea:
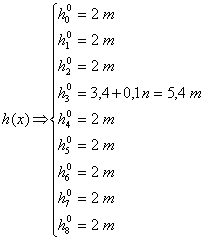
Sa se analizeze problemele de stabilitate numerica a schemei cu diferente finite explicite (FD up-wind), considerandu-se trei variante de discretizare:
Varianta 1
t - pasul de discretizare a timpului
Δt = 50 s
x - pasul de discretizare a spatiului
Δx = 100 m
Calculele se vor efectua pentru cel putin 8 pasi de timp (t8 = 400 s).
Varianta 2
t - pasul de discretizare a timpului
Δt = 100 s
x - pasul de discretizare a spatiului
Δx = 100 m
Calculele se vor efectua pentru cel putin 4 pasi de timp (t4 = 400 s).
Varianta 3
t - pasul de discretizare a timpului
Δt = 200 s
x - pasul de discretizare a spatiului
Δx = 100 m
Calculele se vor efectua pentru cel putin 2 pasi de timp (t2 = 400 s).
Se vor compara si comenta rezultatele celor trei variante de calcul a propagarii undei de viitura.
Rezolvare
Varianta 1
t - pasul de discretizare a timpului
Δt = 50 s
x - pasul de discretizare a spatiului
Δx = 100 m
![]()
![]() - schema este stabila
- schema este stabila

Calculele si rezultatele se pot vedea in tabelul si graficul urmator
|
Nr. Sectiune i |
t₀ = 0 |
t₁ = 50 s |
t₂ =100s |
t₃ =150s |
t₄ =200s |
t₅ =250s |
t₆ =300s |
t₇ =350s |
t₈ =400s |
|
j = 0 |
j = 1 |
j = 2 |
j = 3 |
j = 4 |
j = 5 |
j = 6 |
j = 7 |
j = 8 |
|
|
hi (m) |
hi (m) |
hi (m) |
hi (m) |
hi (m) |
hi (m) |
hi (m) |
hi (m) |
hi (m) |
|
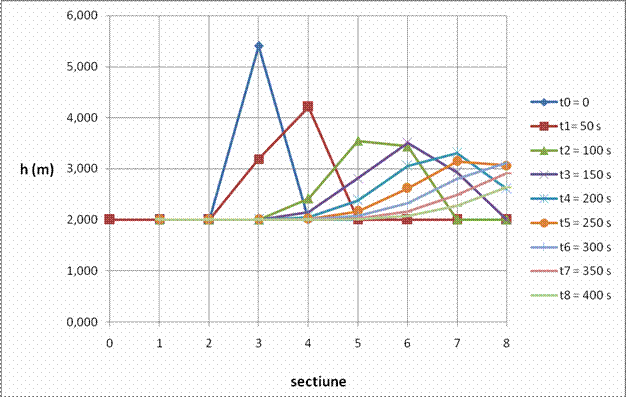
Varianta 2
t - pasul de discretizare a timpului
Δt = 100 s
x - pasul de discretizare a spatiului
Δx = 100 m
![]()
![]() - schema este instabila
- schema este instabila

Calculele si rezultatele se pot vedea in tabelul si graficul urmator
|
Nr. Sectiune i |
t₀ = 0 |
t₁ = 100 s |
t₂ = 200 s |
t₃ = 300 s |
t₄ = 400 s |
|
j = 0 |
j = 1 |
j = 2 |
j = 3 |
j = 4 |
|
|
hi (m) |
hi (m) |
hi (m) |
hi (m) |
hi (m) |
|
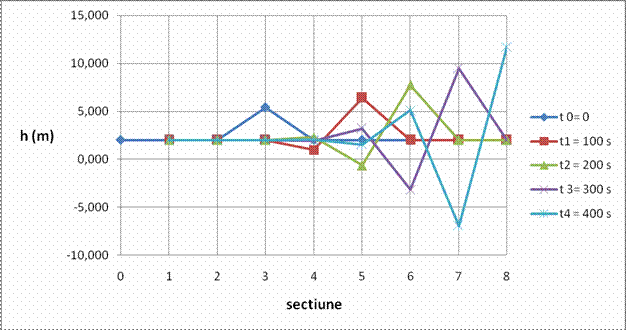
Varianta 3
t - pasul de discretizare a timpului
Δt = 200 s
x - pasul de discretizare a spatiului
Δx = 100 m
Calculele se vor efectua pentru cel putin 2 pasi de timp (t2 = 400 s).
![]()
![]() - schema este instabila
- schema este instabila

Calculele si rezultatele se pot vedea in tabelul si graficul urmator.
|
Nr. Sectiune i |
t₀ = 0 |
t₁ = 200 s |
t₂ = 400 s |
|
j = 0 |
j = 1 |
j = 2 |
|
|
hi (m) |
hi (m) |
hi (m) |
|
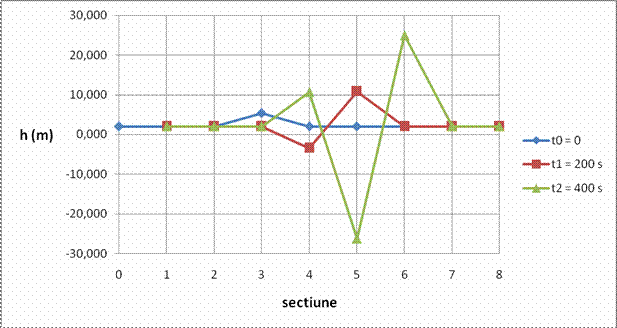
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 2325
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2026 . All rights reserved