Determinarea nivelului optim al productiei

Determinarea nivelului optim al productiei

Pe piata actioneaza o singura firma care produce un singur produs , in cantitati pe care le stabileste liber,in functie de circumstante.

Se presupune ca toata cantitatea de produse scoasa pe piata de catre firma se vinde .

Presupunem ca pretul de cumparare al produsului scade proportional in raport cu cantitatea produsa si lansata pe piata ; deasemeni, costul unitar de productie scade proportional cu aceasta cantitate.

Conform acestor ipoteze , avem urmatoarele relatii :

- notam prin "x" cantitatea de produse lansata pe piata de catre firma ;

- atunci costul unitar de productie , notat prin C₁(x) , are aspectul :

C₁(x) = a - b∙x

- pretul de cumparare al produsului , notat prin C₂(x) , este dat de relatia

C₂(x) = m - p∙x .

Aici a , b , m , p sunt constante pozitive presupuse cunoscute .

Vom presupune ca avem p > b .

Deoarece aceste costuri sunt pozitive , trebuie sa avem

(1) .

Mai mult , costul de productie trebuie sa fie mai mic decat pretul de vanzare al produsului , deci trebuie sa mai fie indeplinita si relatia

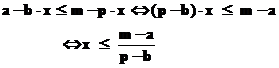(2).

Observare : valorile lui "x" determinate din relatiile ( 1 ) , ( 2 ) constituie ceeace vom numi

aici orizontul economic al activitatii firmei . Asadar , avem

Cu aceste ipoteze si notatii , avem urmatoarele :

- cheltuielile totale de productie sunt date de :

E₁ = x∙ C₁(x) = x∙( a - b∙x)

- incasarile totale rezultate in urma desfacerii produsului pe piata vor fi date

de relatia :

E₂ = x∙ C₂(x) = x∙( m - p∙x) .

- beneficiul firmei va fi :

E(x) = E₂ - E₁ = x∙( m - p∙x) - x∙( a - b∙x) .

Expresia

este un trinom de grad doi in raport cu variabila "x" : cum am presupus ca avem b < p ,

acest trinom prezinta un punct de maxim , corespunzator valorii

.

In final : daca firma doreste sa obtina beneficiu total maxim , va trebui sa fabrice cantitatea

x^* de produs .

Valoarea efectiva a beneficiului maxim va fi :

END