Jocuri strategice

Jocuri strategice

Domeniul cel mai propice pentru folosirea metodelor de joc in vederea deciziilor este cel al relatiilor competitionale dintre indivizi independenti, compartimente sau grupuri de indivizi, organizatii si grupuri de organizatii. Este vorba de relatii conflictuale.

Teoria trateaza numeroase tipuri de jocuri strategice. O sistematizare a acestora este prezentata in schema din figura 4.3

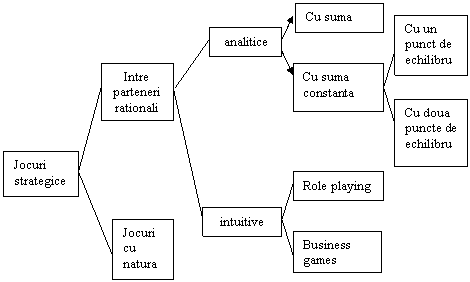
Fig. 4.3 Schema tipurilor de jocuri strategice

O mare parte din jocurile intre parteneri rationali, si anume cele analitice, sunt asociate unor probleme relativ bine structurate cu caracter repetitiv. De exemplu, concurenta dintre ofertantii de produse similare pe o piata libera, sau competitia dintre compartimentele unei firme pentru adjudecarea unui cuantum cat mai mare din fondul de investitii alocat.

Jocurile intuitive, dintre care in schema s-au inclus "role playing" (simulari de roluri manageriale) si "business games" (jocuri de afaceri), sunt asociate unor probleme conflictuale slab structurate.

Jocurile cu natura fac parte din domeniul deciziilor in conditii de incertitudine. Proiectantul, planificatorul, antreprenorul sunt considerati parteneri rationali. Ei isi formuleaza variantele lor de actiune, iar natura se poate manifesta cu starile ei firesti, mai mult sau mai putin favorabile fata de actiunile omului.

Prezentarea modului in care se folosesc jocurile, in vederea adoptarii deciziilor, incepe cu jocurile analitice.

1. Jocuri strategice cu suma zero

Jocul strategic de doua persoane cu suma zero, poarta aceasta denumire deoarece "castigul" unuia dintre jucatori (+a) este egal cu "pierderea" celuilalt jucator (-a), asa incat, efectuand suma acestora, se obtine valoarea zero.

In regulile unui joc intervin urmatoarele elemente:

- cel putin doi jucatori: maximizantul J₁ si minimizantul J₂;

- strategiile sau variantele de joc, S_i (i=1,m) in cazul lui J₁, si s_j (j=1,n) in cazul lui J₂;

-matricea de plati, sau matricea consecintelor jocului:

A=║a_ij║

unde a_ij reprezinta platile sau castigurile jucatorului maximizant (J₁), corespunzatoare cazului in care el aplica strategia sa S_i, iar minimizandu-l J₂ ii raspunde cu strategia sa s_j.

Jocurile de doua persoane cu suma nula, definite de elementele de mai sus, sunt considerate jocuri cu informatie completa: fiecare din partenerii de joc isi cunoaste strategiile sale si pe cele ale adversarului, precum si matricea de plati asociata. Sursa de cunoastere o formeaza datele statistice. Asadar, aceste jocuri sunt in cele mai numeroase cazuri repetitive.

In atingerea scopului lor, partenerii de joc folosesc criterii de decizie proprii.

Astfel, maximizantul J₁, foloseste criteriul "MAXIMIN". El pleaca de la ipoteza ca minimizantul este inteligent si informat asupra jocului. Ca atare, atunci cand matricea de plati A contine profituri, cota pe piata, cifra de afaceri sau alte "castiguri" ale lui J₁, va selecta pe fiecare linie valoarea minima (min a_ij) si va

j

adopta linia care-i va asigura valoarea (max min a_ij). Aceasta regula ii este

i j

impusa de minimizant care, asa cum rezulta si din dimensiunea atribuita, va incerca sa-l determine sa castige cat mai putin posibil, deci il preseaza spre valoarea min a_ij.

j

Asadar, el alege linia cu valoarea minima cea mai convenabila pentru sine, adica cel mai mare minim.

Minimizantul j₂ isi selecteaza decizia dupa criteriul "MINIMAX". Stie ca maximizantul vrea sa castige cat mai mult din competitie si atunci selecteaza pe fiecare coloana valoarea a_ij care este cea mai mare, (max a_ij), si va alege coloana cu cea mai mica valoare maxima, adica (min max a_ij).

j i

Utilizarea de catre jucatori a acestor doua criterii echilibreaza jocul intr-un punct, iar "departarea" vreunuia dintre competitori de acesta ii aduce numai prejudicii. Acest punct indica valoarea jocului.

Se cunosc doua tipuri de strategii care rezulta din rezolvarea jocurilor strategice astfel definite:

a)      strategii pure

b)      strategii mixte

Strategiile pure apar atunci cand, dupa ce jucatorii isi aplica propriile criterii de decizie, se verifica ecuatia:

max min a_ij= min max a_ij

i j j i

Rezultand pentru fiecare jucator cate o singura strategie optima, respectiv pentru J₁, strategia Si si pentru J₂ strategia s_j.

Valoarea a_ij care satisface relatia de mai sus este chiar valoarea jocului si se noteaza cu v. Daca v>0, castiga maximizantul. Daca v<0, castiga minimizantul. Daca v= o, rezultatul este de egalitate.

2. Jocuri strategice cu suma constanta

In jocurile strategice cu suma constanta se ofera o "miza" de joc care este adjudecata de catre parteneri proportional cu calitatea strategiilor utilizate.

In timp ce in jocurile cu suma nula se foloseste o singura matrice de plati cu castigurile jucatorului maximizant, in aceste jocuri se folosesc, de regula, doua matrici, si anume o matrice de forma:

A=║a_ij║

ale carei elemente a_ij reprezinta castigurile maximizantului si o matrice de forma:

B=║b_ij║

cu elementele b_ij reprezentand castigurile minimizantului.

Din acest motiv jocurile de acest fel se numesc bimatriceale. Jocurile cu suma constanta pot avea unul sau doua puncte de echilibru.

In jocurile cu un punct de echilibru, fiecare jucator rezolva problema identificand strategiile care ii maximizeaza rezultatul. Se vor inregistra doua valori ale jocului. Prima valoare v^* pentru maximizant:

v^*=X*AY*

Unde v* reprezinta speranta matematica a castigurilor sale cand foloseste strategiile optime X*=(x*₁, x*₂,., x*_m), iar minimizantul ii opune strategiile sale optime Y*= (y*₁,y*₂,..,y*_n). A doua este valoarea u* pentru minimizant:

u*=X*BY*

unde u* este speranta matematica a castigului minimizantului in conditiile folosirii de catre acesta a strategiilor Y*= (y*₁, y*₂, .y_n*), la care maximizantul raspunde cu

X*= (x*₁, x*₂.,x*_m).

Ca o remarca speciala se poate mentiona ca daca unul dintre jucatori nu-si cunoaste exact veniturile potentiale, sau daca doreste sa utilizeze un model de rezolvare mai simplu, atunci ambii jucatori pot apela la o singura matrice de plati, A sau B dupa caz. Vor rezulta aceleasi strategii optime X* si Y* ca acelea asociate sperantelor matematice.

Jocurile cu suma constanta pot fi dezvoltate sub forma de cooperari. In acest caz apar doua puncte de echilibru ale jocului. Un punct de echilibru identificat ca mai inainte, cand fiecare jucator optimizeaza strategiile sale urmarind exclusiv interesul propriu, rezultand cele doua valori ale jocului (v*, u*), si un al doilea punct de echilibru rezultat din cooperarea jucatorilor care va avea, la randul sau, alte doua valori ale jocului v pentru maximizant si u pentru minimizant. Cel de-al doilea punct de echilibru va fi consistent daca si numai daca se realizeaza conditia:

(v, u) >(v*, u*)

care constituie asa-numitul principiu al rationalitatii individuale. El se traduce prin sintagma: cooperezi cu altul daca castigi mai mult decat ai actiona independent.

Valorile jocului rezultate din cooperare pot fi redate sub forma sperantelor matematice:

Partenerilor nu le ramane decat sa stabileasca seturile optime de strategii in acest caz,

  si

Acestea se stabilesc prin intelegere. De exemplu, doua firme care concureaza pentru ocuparea unei pe piete care actioneaza si firme terte, pot sa isi exercite independent politicile lor de promovare, preturi, conditii de plata, dar pot sa coopereze in ceea ce priveste serviciile post comerciale acordate clientilor. Acestea pot conveni ambelor firme datorita economiilor ce se obtin pe baza efectului de scara a volumului de activitati ce pot fi realizate in comun. Cooperarile de acest fel maresc castigurile firmelor chiar daca in restul politicilor lor se comporta concurential.

3. Jocuri strategice de tip "Business Games"

Jocurile de tip "Business Games" sunt simulari ale desfasurarii unor procese economice in conditii concurentiale prin care proprietarii sau reprezentantii lor (managerii), individual sau in echipe, conduc afaceri, fiecare partener de acest fel urmarind sa realizeze cele mai bune rezultate in comparatie cu competitorii.

Jocurile economice pot fi macro si microeconomice. Cele mai raspandite sunt de nivel microeconomic care , la randul lor, pot fi generale si specializate, sau functionale. Jocurile de tip general se ocupa de dirijarea evolutiei firmelor in contextul social-economic in care functioneaza. Jocurile specializate reprezinta simulari ale rezolvarii unor probleme partiale din cadrul firmelor. Cele mai multe dintre acestea rezolva genuri de probleme care revin diferitelor functiuni ale firmelor. De aceea se mai numesc si jocuri functionale. Exemple de astfel de jocuri sunt cele care se ocupa de probleme de marketing, probleme de mentenanta, finantarea programelor etc.

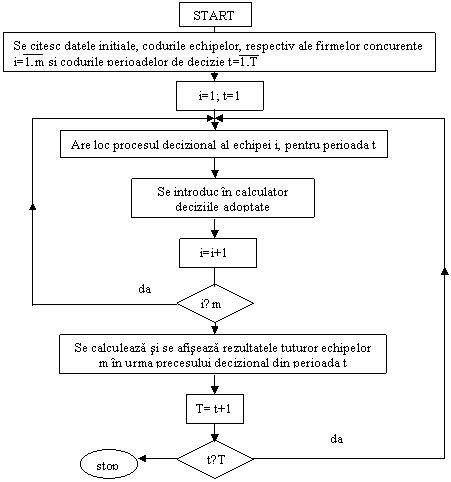
Pentru intelegerea structurii simularilor de tip business games se prezinta in continuare mecanismul desfasurarii unui joc de tip general referitor la o firma industriala.

nu

Fig.4.4 Schema bloc a unui joc de afaceri

nu