Analiza capabilitatii proceselor de fabricatie

Analiza capabilitatii proceselor de fabricatie

3. Determinarea capabilitatii in cazul proceselor de mare "productivitate" (MP)

3. Determinarea capabilitatii in cazul proceselor de mare "productivitate" (PM)

Stabilirea capabilitatii in cazul proceselor de mare "productivitate" se face prin intermediul esantioanelor, care se formeaza cu ajutorul "metodei probelor reduse", numita si metoda probelor curente. Aceasta metoda se aplica cand:

-procesul de productie nu permite luarea unui numar prea mare de produse in ordinea obtinerii lor, pentru ca l-ar stanjeni:

-procesul de productie are o "productivitate" foarte ridicata;

-determinarea valorilor caracteristicii este anevoioasa si costisitoare.

Formarea esantioanelor consta in culegereaa "r"probe din productia masinii, care contin un numar egal de exemplare "n". Extragerea se opreste in momentul cand numarul total al elementelor este N=r n. Probele succesive sunt situate in asa fel incat orice perturbare a omogenitatii sa fie identificata cu probabilitate suficienta.

In practica volumul probelor este cuprins intre 4-10, pentru caracteristicile masurabile si intre 20 si 60 pentru caracteristicile atributive, iar numarul probelor, aproximativ 25.

Pentru fiecare proba se calculeaza media , dispersia s², respectiv abaterea medie patratica s , amplitudinea imprastierii R, si alti parametrii statistici.

Abaterea medie patratica s se calculeaza cu relatia:

unde: a_n este media raportului dintre amplitudine si abaterea medie patratica, adica:

Valorile lui a_n sunt functie de n si se dau in tabele.

Parametrii statistici permit estimarea parametrilor populatiei generale. Pentru aceasta este insa necesar ca probei sa fie estimatii ale unuia si aceluiasi parametru teoretic. Astfel spus este necesar ca probele obtinute sa fie omogene, adica sa aiba aceleasi medii si dispersii. Deci trebuie testate ipotezele:

-pentru medii: H₀:m₁=m₂=.=m_n, cu alternativa H₁: cel putin doua medii diferite;

-pentru dispersii: H₀:s s s_n, cu alternativa H₁: cel putin doua dispersii diferite;

Ipoteza cu privire la omogenitatea probelor din punct de vedere al mediei se face cu ajutorul analizei dispersionale, testul t, testul Dixon, testul Duncan, testul lui Link si Wallancce, iar pentru dispersii cu ajutorul testului c , testul lui Cochran si altele.

3.1. Verificarea omogenitatii dispersiilor

Testul c . Pe baza datelor celor r probe , compuse din n₁, n₂, ., n_r unitati se calculeaza dispersiile s₁, s₂, ., s_r. Daca dispersiile sunt extrase din aceeasi populatie a carei dispersie generala este cunoscuta, se pot calcula r variabile c determinate cu relatiile:

care au o repartitie c cu n n n_r grade de libertate unde n_i=n_i-1. Valorile c se compara apoi cu valoarea c _{a ni)} corespunzatoare nivelului de semnificatie asi numarului gradelor de libertate n_i

Dispersia pentru care obtinem 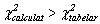se considera nefiind o estimatie a dispersiei generale si se elimina din calculul acesteia.

De multe ori in practica dispersia generala s nu se cunoaste si se inlocuieste cu estimatia sa s². In acest caz relatiile anterioare devin:

valori care urmeaza aproximativ repartitia c cu n n n_r grade de libertate.

Tot in acelasi scop, al omogenizarii dispersiilor, se poate utiliza testul Cochran, care are forma:

Daca valoarea calculata cu relatia lui g_i pentru dispersia esantionului "i" gi<g_v;k;a, se poate constata ca nu sunt motive sa presupunem ca dispersia respectiva, suspecta de a fi o abatere de la masa dispersiilor , nu estimeaza dispersia generala s . Valorile g_v;k;a se dau tabelar.

In situatia in care se elimina un numar prea mare de dispersii, justetea rezultatului final este pusa sub semnul intrebarii, caz in care este necesara efectuare unei temeinice analize tehnologice de specialitate, care sa dubleze interpretarea statistica a rezultatelor.

Aplicatie

Determinarile efectuate asupra unui numar de 250 epruvete de otel luate din 25 de sarje de otel au condus la obtinerea datelor din tabelul de mai jos, referitoare la caracteristica de calitate "rezistenta la rupere"

Se cere sa se stabileasca daca dispersiile calculate pe baza masuratorilor obtinute din verificarea lotului supus controlului, sunt omogene.

Se observa ca cea mai mare dispersie este cea corespunzatoare sarjei a 6-a, =2.2. Se calculeaza valoarea curelatia:

Pentru a=0.05 si u=9 obtinem din tabelele . Intrucat 13.56908<16.9 rezulta ca sarja a-6-a nu difera de a celorlalte sarjesi in consecinta nu se va elimina din calculul dispersiei generale. Rezulta ca dispersiile obtinute din rezultatele masuratorilor caracteristicii de calitate analizata sunt omogene.

3.2. Verificarea omogenitatii mediilor

se pune nu numai procesele MP ci si a celor de mare productivitate atunci cand graficul timp evidentiaza existenta mai multor distributii instantanee. Este necesar ca inainte de calcularea mediei generale ca estimator al mediei procesului, cu relatia sa se tr3steze egalitatea (omogenitatea) sirului de medii partiale. Testarea omogenitatii sirului de medii partiale se poate face cu ajutorul analizei dispersionale, testul Dixon, testul Link si Wallance.

Analiza dispersionala. Fie un eveniment care furnizeaza valorile x₁, x₂, ., x_n ale unei variabile, valori care pot fi privite ca variabile aleatoare independente repartizate normal N(m_i, s). Se considera ca avem una si aceeasi dispersie s (necunoscuta), mediile m_i, pot varia in functie de anumiti factori care intra in experiment. Scopul experimentului este de a cerceta variabilitatea mediilor si ca aceasta variabilitate poate fi testata pe baza datelor de observatie.

Analiza dispersionala in functie de valorile de observatie se poate aplica in doua variante:

-modelul de analiza dispersionala unifactoriala;

-modelul de analiza dispersionala multifactoriala.

a. Modelul de analiza dispersionala unifactoriala. Presupune gruparea datelor observate in "r" grupe, fiecare grupafiind 1 £ i £ r si contine n_i variabile, fiecare urmand o lege normala N(m_i, s), unde s.este independenta de "i". Fie :grupul 1: x₁₁, x₁₂, ., x_1n, x_1jIN(m_i, s £j£n₁;

grupul 2: x₂₁, x₂₂, ., x_2n, x_2jIN(m_i, s £j£n₂;

grupul i: x_i1, x_i2, ., x_in, x_inIN(m_i, s £j£n_i;

grupul r: x_r1, x_r2, ., x_rn, x_rnIN(m_r, s £j£n_r.

Notand cu x_ij unde 1£i£r, 1£j£n_i, cea de-a j-a valoare din cel de-al i-lea grup, atunci se poate pune in evidenta media aritmetica a celei de-al i-lea grup,

si media aritmetica a tuturor valorilor x_ij:

unde:

Suma patratelor abaterilor de la media aritmetica x este: , care mai poate fi scrisa si sub forma :

Deoarece suma dublului produs este nula, se poate scrie identitatea . Cum sunt forme patratice in variabile xij, se cunoaste ca Q² poate fi transformata ortogonal intr-o suma de patrate si deci are rangul n-1.

este suma patratelor a r forme liniare care satisfac identitatea:

si prin urmare rangul formei patratice este cel mult egal cu r-1. Analog este suma a n forme liniare L_ij=x_ij-x_i , care satisfac r relatii independente, cu rangul n-r.

Rangul lui Q² este egal cu suma rangurilor lui si , respectiv n-1=(r-1)+n-r, cea ce ne da posibilitatea sa afirmam ca formele si sunt independente.

Pe baza datelor de observatie se verifica ipoteza nula:

H₀:m₁=m₂=.=m_r=m.

Transformata ortogonala mentionata ne permite sa scriem ca: sunt variabile aleatoare c cu n-1, r-1 si respectiv n-r grade de libertate:

In continuare se poate alcatui variabila F a testului F cu relatia:

unde: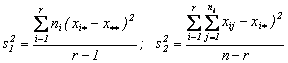

Daca se fixeaza un nivel de incredere 0<a<<1 (in practica se ia 0<a<0.05), atunci putem determina F_a:r-1:n-r astfel incat:

P(F_r-1:n-r>F_a:r-1:n-r a

Aplicarea testului F se face astfel:

-se calculeaza R_r-1,n-r dupa formula de mai sus;

-se fixeaza nivelul de semnificatie a

-se cauta in tabel valoarea lui F_a:n-1;n-r

-se compara cu valoarea calculata F_n-1;n-r;

-daca valoarea calculata depaseste valoarea tabelara, atunci nu sunt motive sa se accepte ipoteza H₀:m_i=m, 1£i£r si deci se va respinge. In caz contrar se accepta ipoteza H₀.

Pentru modelul de analiza dispersionala unifactoriala se alcatuieste schema de calcul din tabelul nr. 1. pe baza testului F.

Tabelul nr. 1

QBS. 1. In cazul cand r=2 verificarea egalitatii mediilor revine la aplicarea testului t.

2. cand se aplica testul F trebuie sa se tina seama de raportul pentru obtinerea valorii lui F deoarece se gasesc tabele pentru valorile lui F>1 si deci trebuie sa se puna la numarator dispersia cu valoare mai mare.

Se observa ca ori de cate ori valoarea lui F calculata este mai mica decat unitatea, ipoteza se accepta asa ca practic nu se mai procedeaza la verificare prin cautarea in tabele.

Se observa ca exista identitatea:

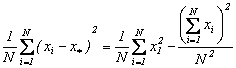
Pe baza acestei identitati putem scrie schema de calcul sub forma din tabelul nr. 2.

Tabelul nr. 2

Aplicatie

Un producator de bunuri de consum produce baterii. Pe baza unor exprimente s-a constatat ca durata de descarcare a acestora urmeaza o repartitie normala. Producatorul produce acelasi tip de baterie prin trei procese tehnolgice de fabricatie diferite. Pe baza unui numar de masuratori efectuate din fiecare tip de proces tehnologic se cere sa se verifice ipoteza ca durata medie de descarcare pentru fiecare tip de baterie este aceeasi.

Rezultatul masuratorilor este trecut in tabelul urmator

In baza datelor de observatie inregistrate in tabelul de mai sus se obtin mediile aritmetice: x₁=553.3333;; x2=535; x₃=563.5; x_1,2,3=552.3077

In conformitate cu schema de calcul a modelului de analiza dispersionala unifactoriala se obtin datele din tabelul de mai jos.

Pe baza datelor se calculeaza testul F:

La nivelul de semnificatie a=0.05, se obtine din tabelele pentru variabila F valoarea F_0,05;2;23=3.42. Comparand valorile obtinute : F3;22=1.64<3.42=F_0.05;3;22 ceea ce permite a se trage concluzia ca nu avem motive sa respingem ipoteza asupra egalitatii duratelor medii de descarcare

b. Modelul de analiza dispersionala multifactoriala

Consideratiile facute pentru modelul de analiza dispersionala unifactoriala se generalizeaza la cazul cand valorile de observatii se pot clasifica intr-un sistem mai complicat de grupuri si subgrupuri de diferite ordine. In general, variabilele vor fi indicate prin doi sau mai multi indici.Ca in cazul mentionat vom presupune ca valorile x_i ale variabilei sunt independente si ca sunt repartizate normal N(m_i;s) cu s independent de i.

Pentru orice sistem de grupare utilizat intr-o problema particulara putem considera sume patrate de abateri mai mult sau mai putin analoge cu sumele patrate si de la modelul unifactorial. Asadar, este posibil sa obtinem o relatie de forma:

unde Q_i(1£j£k) sunt sume de patrate de forme liniare in xi astfel incat intre rangurile formelor patratice , , ., exista relatia: n-1=r₁+r₂+.+r_k, cu r_j rangul formei patratice, 1£j£k).

Rationand ca in cazul analizei dispersionale unifactorile rezulta ca in ipoteza H₀:m₁=m₂=.=m_k variabilele sunt variabile cu r₁, r₂, .,r_k grade de libertate respectiv si putem pune in evidenta diferite variabile aleatoare F.

Testul Dixon

Pentru fiecare proba se calculeaza media acestuia care se ordoneaza apoi crescator. Notam cu m₁, m₂, m₃ mediile cu valorile cele mai mici, iar cu M₁, M₂, M₃ mediile cvalorile cele mai mari, obtinand:

m₁<m₂<m₃<.<M₃<M₂<M₁.

In continuare, atat pentru cea mai mica medie, caty si pentru cea mai mare medie se calculeza rapoartele r_ij, care se compara cu cele care rezulta din tabelul anexa determinate pentru nuvelul de semnificatie 1%. Daca valoarea calculata depaseste valoarea tabelara, esantionul se respinge ca necorespunzator. Dupa eliminare se repeta procedeul pentru eliminarea esantionului urmator daca este cazul.

Testul Link-Wallance. Este un test rapid pentru analiza dispersionala si comparatii multiple ale valorilor medii, mult mai sever decat testu lui Dixon. Acest test presupune ca repartitiile sa fie aproximativ normale, dispersiile egale si esantioanele de aceeasi marime n.

Ipoteza nula m₁=m₂==m_i=m_r se acepta daca:

unde este amplitudinea de imprastiere a valorilor medii;

R_i -amplitudinea esantioanelor (grupelor).

Valoarea critica k se poate extrage din tabele in functie de n si r dati si pentru a=0,05 respectiv a

Comparatiile multiple ale valorilor medii cu diferenta intre valorile medii sunt semnificative daca: