Universitatea "Ovidius" Constanta

Facultatea de Matematica si Informatica

Specializarea MCTIM I

RECONSTRUCTIA IMAGINILOR IN TOMOGRAFIA COMPUTERIZATA

PROIECT

Pornind de la o matrice si de la un vector ce reprezinta imaginea exacta, dorim sa reconstruim aceasta imagine dupa modelul reconstructiilor din tomografia computerizata, utilizand mai multi algoritmi.

Se da matricea , definita pe cu si are trei valori: . De asemenea avem vectorul care reprezinta imaginea exacta.

Pentru inceput desenam imaginea exacta descompusa in pixeli () la fel ca in figura urmatoare. Acolo unde este desenat vom completa matricea cu 1 iar unde este gol cu 0. Vom citi matricea de la stanga la dreapta pe linii si vom obtine vectorul cu 144 de elemente.

2 3 4 5 6 7 8 9 10 11 12

Imaginea exacta data de vectorul in Matlab este urmatoarea:

Construim termenul liber astfel: . Apoi aflam vectorul

Imaginea obtinuta cu vectorul este:

Pentru

Pentru

Pentru

Partea I: Metode iterative: Jacobi

Generam sistemul consistent utilizand metoda Jacobi.

Teorema Elfving(2000)

Pentru oricare termenul generat cu metoda Jacobi converge

solutia .

Fie , reprezinta linia din matricea si

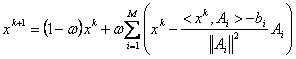, unde se numeste parametru de relaxare si ( reprezinta numarul de linii ale matricei

Pentru aceasta metoda avem trei matrice de diferite marimi

Pentru matricea , imaginea obtinuta prin metoda Jacobi pentru la de iteratii este:

Pentru matricea imaginea obtinuta prin metoda Jacobi pentru la de iteratii este:

Pentru matricea imaginea obtinuta prin metoda Jacobi pentru la de iteratii este:

Pentru matricea imaginea obtinuta prin metoda Jacobi pentru la de iteratii este:

Pentru matricea imaginea obtinuta prin metoda Jacobi pentru la de iteratii este:

Pentru matricea imaginea obtinuta prin metoda Jacobi pentru la de iteratii este:

Partea II: Metode mixte- Kerp

a)      Perturbarea

- generarea vectorului perturbator

Membrul drept al expresiei (unde este imaginea exacta) se perturba ca mai jos:

, cu

Unde pert este un vector generat aleator (care apoi este acelasi pentru toate experimantele) normalizat astfel: norm(pert)=1

norma Euclidiana a vectorului z

- construirea termenului liber perturbat

Pentru o imagine exacta vom construe un system consistent cu:

, apoi va fi astfel perturbat:

, , unde rand va fi un vector aleator generat cu norma unu.

b)Metoda Kerp

Fie , reprezinta linia din matricea si reprezinta coloana din matricea

Fie si

Teorema (C.Popa,1998)

Pentru exista

Pentru matricea A:36*144 imaginea obtinuta prin metoda Kerp pentru omega=1, alfa=1, epsilon=5 si numarul de iteratii 1000:

Pentru matricea A:144*144 imaginea obtinuta prin metoda Kerp pentru omega=1, alfa=1, epsilon=5 si numarul de iteratii 1000:

Pentru matricea A:576*144 imaginea obtinuta prin metoda Kerp pentru omega=1, alfa=1, epsilon=5 si numarul de iteratii 1000:

Partea III: Algoritm cu proiectii oblice- CAV

Fie: si

, , unde

, unde .

Adica reprzinta numarul de elemente nenule de pe coloana j din A.

Idee: intr-un numar mic de iteratii(30, 40, 50) imaginea care se obtine este buna.

Pentru matricea A:36*144 imaginea obtinuta prin metoda CAV pentru numarul de iteratii 50:

Pentru matricea A:144*144 imaginea obtinuta prin metoda CAV pentru numarul de iteratii 50:

Pentru matricea A:144*144 imaginea obtinuta prin metoda CAV pentru numarul de iteratii 1000:

Pentru matricea A:576*144 imaginea obtinuta prin metoda CAV pentru numarul de iteratii 1000:

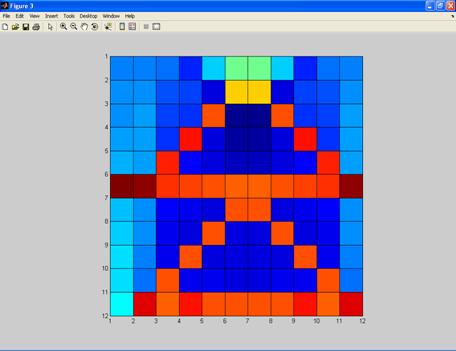
Pentru matricea A:576*144 imaginea obtinuta prin metoda CAV pentru numarul de iteratii 50:

Partea IV: CONCLUZII

Pentru fiecare algoritm folosit s-au calculate si afisat errorile si rezidurile dupa formulele:

Daca acestea descresc de la o iteratie la alta inseamna ca implementarea algoritmului a fost corecta.

Criterii de oprire cunoscute:

Cu un numar de iteratii prestabilit (acesta a fost folosit in implementarea algoritmilor)

Rezidual

Altele

Se observa ca folosirea algoritmului lui CAV este cea mai indicata pentru reconstructia de imagini, deoarece la un numar mai mic de iteratii obtinem o imagine mai apropiata de cea reala.

De asemenea se observa pentru toti algoritmii folositi ca claritatea imaginii reconstruite depinde si de dimensiunea matricii A, adica cu cat dimensiunea ei este mai mare cu atat imaginea este apropiata de cea reala.