| CATEGORII DOCUMENTE |
| Agricultura | Asigurari | Comert | Confectii | Contabilitate | Contracte | Economie |
| Transporturi | Turism | Zootehnie |
MODELELE PREVIZIUNII
Este necesar deci, ca pornind de la o serie cronologica cunoscuta care descrie comportarea sistemului pana in prezent sa se determine functia y=f(t) care aproximeaza cel mai bine (cu o anumita eroare) comportarea reala a sistemului in viitor. Timpul 0 (originea) se alege arbitrar ca fiind timpul pentru prima valoare din seria cronologica.
Evolutia viitoare a unui sistem economic este o suma :
y=T(t)+C(t)+S(t)+U(t)
unde:
T(t) - este tendinta principala de evolutie ;
C(t) - este componenta ciclica care descrie periodicitati mai mari de un an ;
S(t) - este componenta sezoniera , periodicitati mai mici de un an ;
U(t) - este componenta aleatoare .

O alta notiune importanta este termenul de prognoza definit ca marimea intervalului de timp care separa momentul din viitor fata de prezent.
Daca notam : T - este momentul viitor vizat de prognoza ;
t - este momentul prezent cunoscut ;
atunci orientativ se numeste prognoza pe termen :
- scurt daca (T-t) < t/3 (1-3 ani) cu eroare
- mediu daca t/3 < (T-t) < t (5-7 ani) cu eroare
- lung daca (T-t) > t (peste 10 ani) cu eroare
Relatiile sunt valabile numia daca timpul primei valori din serie este egala cu zero .

Din pacate nu exista o metoda prin
care sa se determine prin calcul in mod obiectiv tipul curbei care aproximeaza
cel mai bine seria dinamica de care se dispune si alegerea trebuie facuta din
patru tipuri fundamentale :




Pentru aplicarea modelului sezonier (fenomene ciclice) se folosesc dezvoltari FOURIER , analiza armonica .
Alegerea tipului functiei care descrie cel mai fidel norul de puncte se face dupa aspectul curbei obtinute prin reprezentarea grafica a valorilor luand pe abscisa timpul.
Odata aleasa forma functiei , se pot calcula coeficientii ei prin metoda celor mai mici patrate denumita si metoda regresiei.
![]()
Presupunem ca relatia aleasa este in
general de forma :
![]()
![]()
![]() Parametrii ai
functiei nu se pot determina exact deoarece valorile observate , (valorile din seria dinamica) contin
inerent erori aleatoare. Admitem deci ca intre valorile observate si valorile de pe curba aleasa sunt
diferente. Insumam aceste diferente si pentru ca acestea sa nu se compenseze
vom insuma patratele lor .Curba teoretica aleasa descrie cel mai bine norul de
puncte atunci cand suma patratelor diferentelor dintre valorile observate si
cele teoretice calculate este minima . Dar suma amintita este minima cand prima
derivata este zero , astfel ca facand derivate partiale in raport cu fiecare
din parametrii necunoscuti se obtine un sistem de ecuatii din care se pot
calcula acesti parametri .
Parametrii ai
functiei nu se pot determina exact deoarece valorile observate , (valorile din seria dinamica) contin
inerent erori aleatoare. Admitem deci ca intre valorile observate si valorile de pe curba aleasa sunt
diferente. Insumam aceste diferente si pentru ca acestea sa nu se compenseze
vom insuma patratele lor .Curba teoretica aleasa descrie cel mai bine norul de
puncte atunci cand suma patratelor diferentelor dintre valorile observate si
cele teoretice calculate este minima . Dar suma amintita este minima cand prima
derivata este zero , astfel ca facand derivate partiale in raport cu fiecare
din parametrii necunoscuti se obtine un sistem de ecuatii din care se pot
calcula acesti parametri .
Riguros matematic dreptul de a folosi metoda celor mai mici patrate se demonstreaza prin principiul maximei verosimilitati din teoria probabilitatilor .
![]()
Pentru cazul general daca se noteaza
functia aleasa cu :
![]()
si suma patratelor diferentelor cu :
atunci parametri se calculeaza din sistemul de ecuatii :

Exemplu : Cazul distributiei liniare de forma y = a + bt

Suma patratelor diferentelor este :

Se anuleaza derivatele se desfac
parantezele si se obtin coeficientii a
si b :
Pentru masura obiectiva a legaturii dintre marimile yi si ti se calculeaza coeficientul de corelatie cu expresia:

Cand valoarea r , in modul , este apropiata de unitate , corelatia este stransa iar cand r este aproape de zero corelatia este slaba .
Deoarece valorile seriei dinamice sunt la intervale de timp egale calculele se simplifica daca originea timpului se alege astfel ca sa fie adevarata relatia:
![]()
Atunci pentru un numar de valori impar timpii vor fi :
.. -3 -2 -1 0 1 2 3 ..
Pentru numar de valori par timpii vor fi :
In acest caz pentru modelul liniar expresiile de calcul devin :

Aceleasi rationament se face si pentru cazul cand curba aleasa este o parabola de forma :
![]()
Pentru calculul parametrilor modelului se egaleaza cu zero derivatele partiale in raport cu a,b,c. Se obtine un sistem de 3 ecuatii liniare cu 3 necunoscute apoi cu metoda Kramer si Sarus se obtin expresiile de calcul pentru parametri. Daca originea timpului se alege ca sa existe relatiile
![]()
atunci expresiile de calcul pentru coeficientii ecuatiei parabolei sunt :


Pentru masurarea intensitatii
legaturii neliniare se calculeaza raportul de corelatie eta, (diferit de
coeficientul de corelatie) cu expresia :
unde : yi - reprezinta valorile observate ;
y* - reprezinta valorile calculate cu formula stabilita ;
![]()
y - reprezinta media valorilor observate.
Nu uitam ca valorile extrapolate reprezinta tendinta fenomenului care se abate intamplator de la valoarea adevarata. Este deci obligatoriu ca valorilor extrapolate sa li se asocieze un interval de incredere in sens statistic. Pentru aceasta se calculeaza dispersia valorilor seriei dinamice observate fata de valorile obtinute cu modelul teoretic cu expresiile:


Observam ca numarul de grade de libertate este redus cu 2 respectiv cu 3, deoarece parametrii a, b si c au fost estimati folosind valorile aceleiasi serii dinamice.
Folosind distributia Student se poate defini un interval de incredere pentru prognoza obtinuta si pentru un prag de semnificatie impus P. Astfel ca valoarea prognozata se va gasi (va fi cuprinsa) cu (siguranta) probabilitatea P in intervalul definit de:
![]()
Exemplu: Se cunoaste seria cronologica:
Se cere sa se calculeze parametrii modelelor liniar si parabolic si corelatia:

Pentru calcule se recomanda folosirea
unui tabel in care pe coloane se pun toate valorile care intervin in formule ca
sume.
Parametrii modelului liniar sunt:

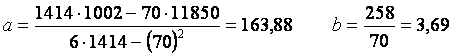
Parametrii modelului parabolic sunt:

Valorile urmatoare cele mai probabile prognozate precum dispersiile seriei cronologice fata de modele sunt:


Comparativ concluzionam ca modelul parabolic descrie mai bine seria cronologica decat modelul liniar deoarece "eta" este mai mare ca r luat in modul.
Un alt model folosit frecvent este modelul exponential de forma :
![]()
Prin logaritmare si substitutii convenabile devine un model liniar :
![]()
![]() Prin analogie cu modelul liniar pentru cazul cand originea
timpului s-a ales astfel ca coeficientii a si b se calculeaza cu expresiile :
Prin analogie cu modelul liniar pentru cazul cand originea
timpului s-a ales astfel ca coeficientii a si b se calculeaza cu expresiile :

Si pentru modelul exponential se calculeaza dispersia:

Exemplu : Se da seria dinamica in coloana din tabel. Se cere sa se calculeze parametrii modelului exponential care o descrie adecvat si urmatoarea valoare prognozata:

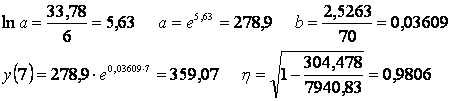
Modelele de prognoza prezentate, obtinute prin metoda celor mai mici patrate (principiul verosimilitatii maxime) garanteaza o buna adecvare la seria cronologica luata ca un tot, desi practic, nici o valoare a seriei nu se regaseste exact in model. Acest lucru este explicabil deoarece am admis ca orice valoare din seria dinamica este afectata inerent de erori aleatoare deci este diferita de valoarea teoretica adevarata.
Modele care se vor discuta in continuare se bazeaza pe ipoteza ca cel putin 2 -3 valori din seria dinamica sunt descrise exact de model.
![]()
Indicele de crestere descrestere este
definit ca raportul dintre doua valori consecutive a seriei cronologice.
Daca se cunoaste valoarea de baza a indicatorului prognozat P0 si indicii de crestere ri pentru perioadele imediat urmatoare de timp egale ca durata atunci exista relatia:
![]()

unde
Indicele mediu de crestere descrestere se mai poate scrie :

Cunoscand deci valorile extreme se poate determina din ultima relatie indicele mediu de crestere (descrestere).
Retinem ca n este numarul valorilor din seria cronologica minus una deoarece notarea valorilor observate incepe cu P si se termina cu Pn
Indicele mediu de crestere descrestere r se poate folosi pentru prognoza in relatiile:
![]()
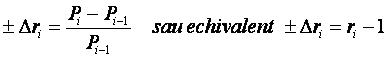
Asa cum a fost definit indicele de
crestere - descrestere acesta este un raport totdeauna pozitiv si nu trebuie
confundat cu cresterea sau descresterea relativa a valorilor prognozate
definite astfel:
Remarcam ca descresterea, spre eosebire de crestere, este negativa.
Exemplul 1: Cu 10 ani in urma realizarile unei statii cf. la tone expediate au fost P0 = 3080 mii tone iar in ultimul an incheiat P9 = 6750 mii tone . Se cere sa se calculeze care a fost cresterea medie anuala .

Valoarea urmatoare se poate calcula astfel:


Valorile (re)calculate
cu modelul obtinut sunt:
Exemplul 2 : Se cunosc cresterile procentuale anuale :
![]()
Se cere sa se calculeze cresterea
medie anuala in procente.
R=9,1%
Exemplul 3 : Se cunosc descresterile anuale in procente :
Xi

Se cere sa se calculeze descresterea
medie anuala in procente .
Exemplul 4 : Stiind ca traficul pe o sectie de circulatie creste in medie anual cu 7,6 % . Se cere sa se calculeze dupa cati ani se dubleaza traficul ?

Evident cu aceleasi metode se pot studia si descresterile.

INTERPOLARE EXTRAPOLARE LAGRANGE
Un alt model care poate fi folosit pentru extrapolarea unei tendinte este metoda Lagrange .
Fiind date punctele prin coordonatele lor :
![]()
Se demonstreaza ca se poate gasi un
polinom de grad n - 1 care sa treaca
(exact) prin cele n puncte .
Polinomul Lagrange este de forma

Deoarece pentru interpolare si extrapolare practic nu se folosesc polinoame de grad mai mare ca 2 vom particulariza expresiile de calcul pentru functiile de gradul I si II .

Dupa cum se observa pentru a gasi polinomul de interpolare Lagrange este suficient sa fie cunoscute numai coordonatele punctelor nu neaparat echidistante pe axa x . Cu ajutorul modelului se pot gasi si functia inversa adica:
y = f(x) sau x = g(y)
Exemplu : Cunoastem valorile unui indicator ca in tabel :

Si se cer valorile lui y(8) si y(13) ?


Un model folosit pentru prognoze este
si cel logistic denumit si curba PEARL REED .
Modelul se foloseste in studiul evolutiei populatiei , estimarea cererii de bunuri de folosinta indelungata , ecolologie si in general modeleaza fenomenele care reprezinta in timp o saturatie .

Se observa pe grafic ca functia logistica este totdeauna pozitiva si monoton crescatoare :
Parametrii a, b, c ai curbei logistice se calculeaza daca se cunosc 3 puncte din seria dinamica echidistante dupa regula ca in tabelul urmator :


Expresiile de calcul sunt atunci :
t - este numarul de valori din seria dinamica care separa doua valori consecutive alese drept yi.
Se recomanda ca valorile yi sa fie alese astfel:
y este ultima valoare din seria cronologica data;
y sa fie cat mai apropiata in timp de prima valoare a seriei.
Exemplu : Se cunosc consumurile anuale ale unui produs de folosinta indelungata ca in tabel: . Se cere: a) Sa se calculeze parametrii a, b si c ai modelului logistic; b) Sa se verifice modelul obtinut recalculand ultima valoare din seria dinamica data; c) Sa se calculeze urmatoarea valoare cea mai probabila; d) Sa se arate ca modelul obtinut tinde asimptotic catre a. Se aleg valorile yi si originea timpului ca in tabel: y =64; y y =116; t=3 adica:



Se observa ca de la timpul 30 la timpul 60 cresterea este nesemnificativa semn ca ne situam in zona de saturatie a cresterii (asimptota).
Spre deosebire de modelul cresterii exponentiale care creste la infinit, modelul logistic are o crestere finita .Aceasta curba este importanta pentru ca modeleaza cresterile din natura, acestea avand o limita finita de crestere.
Un alt model care se poate folosi si in prognoza este modelul functiilor de productie . Cel mai cunoscut este cel propus de C.W.Coob si P.H.Douglas (1928) de forma :
![]()
unde : a,a si b sunt parametrii modelului ;
Q - este volumul productiei ;
M - este volumul fortei de munca ;
F - este volumul fondurilor fixe ;
r - este reziduu de estimatie ca o medie a diferentelor dintre
valorile calculate si cele inregistrate .
Calculul parametrilor functiei se face logaritmand expresia si prin metoda celor mai mici patrate se obtin valorile cautate .

Modelele de evolutie care se bazeaza pe extrapolarea tendintei se pot folosi pentru prognoze pe termen scurt si mediu. De fiecare data este obligatoriu sa se estimeze eroarea probabila atasand prognozei un interval de incredere si un prag de semnificatie ca la orice demers statistic.
Prognozele pe termen lung se intocmesc in doua ipoteze :
cand se presupune ca nu intervin schimbari calitative in evolutia fenomenului studiat atunci se foloseste modelul logistic ;
cand se intrevad schimbari de structura a fenomenului atunci la intocmirea prognozei se folosesc :
a) Metoda Delphi care consta in chestionarea unor experti privind evolutia in timp a sistemului studiat si prelucrarea statistica a opiniilor Chestionarea se face repetat de 2 - 3 ori aducandu-se la cunostinta expertilor rezultatele prelucrarilor statistice intermediare. La fiecare etapa expertii pot sa-si modifice evaluarile anterioare:
b) Metoda scenariilor
c) Metode de simulare, Modele din Dinamica Industriala, modelul INPUT - OUTPUT, Modelul Gompertz etc.
Ciucu G, Craiu V, Introducere in teoria probabilitatilor si statistica matematica. Ed. Didactica si Pedagocica, Bucuresti, 1971.
Ciucu G, Craiu V, Stefanescu A, Statistica matematica si cercetari operationale. Ed. Didactica si Pedagogica. Bucuresti, 1974.
Dorn W.S, McCracken D.D, Metode numerice cu programe in Fortran, Ed. Tehnica, Bucuresti, 1976.
Isaic-Maniu Al., In cautarea optimului, Ed Albatros, 1985.
Moineagu C, Negura I, Urseanu V, Statistica, Editura stiintifica si enciclopedica, Bucuresti 1976.
Rosculet M. Manual de analiza matematica. Ed. Didactica si Pedagogica, Bucuresti, vol.1 si 2, 1967.
Rumsiski L.Z. Prelucrarea matematica a datelor experimentale. Editura tehnica. Bucuresti, 1974.
Sobol I. M., The Monte Carlo method, Mir
Publishers,
Tovissi L., Voda V. Metode statistice. Aplicatii in productie, Editura stiintifica si enciclopedica, Bucuresti 1982.
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 1565
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2026 . All rights reserved