| CATEGORII DOCUMENTE |
| Agricultura | Asigurari | Comert | Confectii | Contabilitate | Contracte | Economie |
| Transporturi | Turism | Zootehnie |
Productivitatea. Legea randamentelor marginale neproportionale
Prin productivitate in sens general intelegem eficienta utilizarii factorilor de productie, determinata ca un raport intre productia obtinuta si factorii de productie consumati. Din subcapitolul precedent cunoasteti deja doua forme ale productivitatii: productivitatea medie si productivitatea marginala si modul in care acestea se pot determina. Un exemplu simplu ne va ajuta sa intelegem mai bine cum se determina productivitatea si ce relatie exista intre productia totala, productivitatea medie si productivitatea marginala pe termen scurt. Sa consideram ca o firma de tricotaje dispune de 5 masini de tricotat si ca poate angaja muncitori in functie de cat de mult doreste sa produca. In functie de numarul muncitorilor angajati, productia totala, productivitatea medie si cea marginala se prezinta astfel:
Tab.6.1. Relatia dintre productia totala, productivitatea medie si
productivitatea marginala
|
Capital (K) |
Munca (L) |
Productie (Q) lunara (bucati) |
Productivitate medie a muncii |
Productivitate marginala a muncii |
Reprezentand grafic acest tabel vizualizam mai usor relatia dintre productivitatea totala, productivitatea medie si cea marginala:
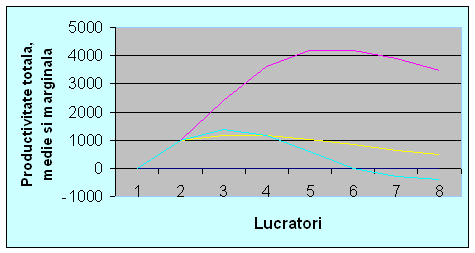
Graf. 6.10. Relatia productivitate totala, productivitate medie si
productivitate marginala
![]() Legenda:
productia
totala
Legenda:
productia
totala
![]() productivitatea
marginala
productivitatea
marginala
![]() productivitatea
medie
productivitatea
medie
Atat din tabel, cat si din grafic, puteti observa urmatoarele:
cand productivitatea marginala este mai mare decat productivitatea medie, productivitatea medie creste;
cand productivitatea marginala este egala cu productivitatea medie, productivitatea medie este maxima;
cand productivitatea marginala este mai mica decat cea medie, productivitatea medie scade;
cand productivitatea marginala este pozitiva, productia totala creste
cand productivitatea marginala este zero, productia este maxima;
cand productivitatea marginala este negativa, productia totala scade; de aceea nici un producator nu va opta pentru o productivitate marginala negativa.
Relatia dintre productivitatea medie si cea marginala formeaza continutul unei legi economice celebre: legea randamentelor marginale neproportionale. Legea randamentelor marginale neproportionale exprima faptul ca pe masura ce se asociaza unitati sucesive dintr-un factor de productie variabil la o cantitate data de factor de productie fix, productivitatea marginala incepe la un moment dat, inevitabil, sa scada. In exemplu anterior, pe masura ce cresteam numarul de muncitori ce reveneau la cele cinci masini de tricotat, la un moment dat, de la doi muncitori, productivitatea marginala a inceput sa scada.
Legea randamentelor marginale descrescatoare este validata de numeroase studii empirice, dar in acelasi timp este si logica. Imaginati-va, de exemplu, ca o firma ar dispune de un hectar de teren si de un numar infinit de muncitori. Daca aceasta lege nu ar actiona, inseamna ca s-ar putea produce infinit pe acel hectar, ceea ce este evident absurd. Tocmai aceasta lege explica de ce tarile cu populatie numeroasa, dar cu suprafata arabila redusa sufera de o lipsa acuta de alimente.
In graficul 6.10. se pot observa trei zone: prima este cea in care productivitatea medie creste, cea de-a doua este cea in care productivitatea medie si cea marginala scad, dar productivitatea marginala este pozitiva si cea de-a treia, in care productivitatea marginala este negativa. Rational, producatorii nu se vor opri cu productia in prima zona deoarece ar insemna ca nu isi exploateaza la maximum potentialul de crestere a productivitatii. De ce? Sa presupunem in exemplul din tabelul 6.1. ca fiecare salariat ocazioneaza firmei o cheltuiala de 900 u.m. si ca firma isi vinde produsele cu 1 u.m./buc.. Pentru primul salariat, firma castiga net 100u.m., pentru cel de-al doilea 300 u.m., pentru cel de-al treilea 300 u.m.; dar ea castiga si cu cel de-al patrulea 150u.m. si pierde abia atunci cand angajaza cinci muncitori (840-900=-60u.m.). In consecinta, firma va angaja patru muncitori mergand pe principiul eficientei economice maxime. Rezulta ca intotdeauna o firma va produce in zona descrescatoare si pozitiva a productivitatii medii a factorului de productie variabil. Veti intelege mai bine legea randamentelor marginale descrescatoare parcurgand subcapitolul urmator dedicat analizei costurilor firmei.
6.3. Costurile de productie
Aduceti-va aminte ca in cel de-al doilea capitol al lucrarii de fata, dedicat raritatii si alegerii, am invatat ca orice alocare a resurselor are un cost: costul de oportunitate. El includea cea mai buna alternativa de productie sacrificata in favoarea celei alese. Din aceasta perspectiva, spunem ca o firma se caracterizeaza prin doua categorii de costuri: costul implicit si costul explicit.
Costul implicit incude cea mai buna alternativa de alocare a resurselor proprii sacrificata de intreprinzator in favoarea obtinerii unei productii date. De exemplu, vom include in acest cost cea mai mare chirie pe care ar fi putut sa o obtina intreprinzatorul pentru cladirile proprii sau dobanda cea mai buna pe care ar fi obtinut-o la capitalul propriu. Observati ca acest cost este sinonim cu costul de oportunitate. In plus, costul implicit este de cele mai multe ori masura pentru profitul normal care este acel profit ce remunereaza contributia exclusiva a intreprinzatorului la activitatea economica.
Costul explicit reprezinta totalitatea cheltuielilor firmei cu factorii de productie cumparati din exterior. Cateva exemple sunt salariile platite angajatilor, cheltuielile cu materiile prime, cu dobanda bancara s.a..
Costul de productie total este suma celor doua costuri, implicit si explicit. Daca din incasarile firmei se scade acest cost se obtine profitul pur, numit si profit economic.
O alta clasificare a costurilor are in vedere criteriul timp; in functie de factorul timp, exista costuri de productie pe termen scurt si costuri pe termen lung.
a) Costurile firmei pe termen scurt
Cea mai importanta clasificare a costurilor pe termen scurt le imparte in costuri fixe si costuri variabile.
Costurile fixe sunt independente de productie, iar cele variabile se modifica o data cu modificarea productiei. De exemplu, dobanda bancara aferenta unui imprumut anual contractat de firma este cost fix, in timp ce cheltuielile cu materiile prime constituie cost variabil. Costul total este suma costurilor fixe si a celor variabile, adica vom scrie ca: CT=CF+CV, in care: CT este costul total, CF costul fix, iar CV costul variabil. Costul total ofera informatii cu privire la cheltuielile globale ale firmei, dar este un criteriu insuficient pentru a aprecia eficienta firmei. Dupa cum deja stiti, putem aprecia eficienta doar comparand cheltuielile cu rezultatele obtinute. De aceea, un indicator economic extrem de important pentru firme este costul mediu. Costul mediu exprima costul pe unitate de produs si se determina cu relatia: CTM=CT/Q, in care CTM este costul mediu, iar Q productia. Asemanator putem calcula costul variabil mediu (CVM) si costul fix mediu (CFM), prin relatiile:
CVM=CV/Q si CFM=CF/Q.
O alta categorie importanta de cost este costul marginal, care exprima costul suplimentar antrenat de ultima unitate de productie realizata. De exemplu, daca o firma producea 100 de perechi de pantofi cu 30 mil. de lei, iar acum produce 101 perechi cu 30,2 mil. de lei, costul marginal este de 0,2 mil. de lei. Relatia de determinare a costului marginal va fi:
CM=DCT/DQ, in care CM este costul marginal.
Pentru variatii infinit de mici ale productiei, putem scrie ca: CM=dCT/dQ, care reprezinta panta curbei costului total. Cu titlu de exemplu, daca functia costului total este de forma: CT=Q2+3Q+100 si dorim sa aflam costul marginal cand productia creste de la 9 la 10 bucati, vom scrie: CM=[CT(10)-CT(9)]/(10-9)=(230-208)/1=22. Daca insa dorim sa aflam costul marginal pentru o productie de 10 unitati, acesta este: CM=dCT/dQ=2Q+3=23.
Grafic, diferenta este si mai evidenta:

![]()

 CT
CT
![]() CF B
CF B
![]()
![]() A
A
![]() CF
CF
![]()
Q
 Relatia
dintre costul mediu si cel marginal releva, la fel ca si cea
dintre productivitatea medie si cea marginala, actiunea legii
randamentelor marginale descrescatoare. Grafic, relatia dintre
costurile medii si cele marginale se prezinta astfel:
Relatia
dintre costul mediu si cel marginal releva, la fel ca si cea
dintre productivitatea medie si cea marginala, actiunea legii
randamentelor marginale descrescatoare. Grafic, relatia dintre
costurile medii si cele marginale se prezinta astfel:



![]()


![]() CVM CM
CVM CM

CFM
Productie
Din graficul anterior puteti remarca urmatoarele:
cand costul marginal este mai mic decat costul mediu, costul total mediu creste pentru orice crestere a productiei; aceasta zona corespunde celei a randamentelor factorial crescatoare din graficul 6.10;
cand costul marginal este egal cu costul mediu, costul total mediu este minim, iar in graficul 6.10. productivitatea medie este maxima;
cand costul marginal este mai mare decat costul mediu, costul total mediu creste pentru orice crestere a productiei, iar in graficul 6.10. randamentele factoriale sunt descrescatoare.
Relatia dintre costul mediu si costul marginal se poate demonstra matematic cu usurinta, pornind de la formula CTM=CT/Q. Astfel, daca derivata de ordinul I este pozitiva, CTM creste, daca este 0 CTM este constant si daca este negativa CTM scade. Cunoastem ca:
dCTM/dQ = [(dCT/dQ)Q-CT]/Q2
Dar dCT/dQ = CM, asa ca:
dCTM/dQ = (CMQ-CT)/ Q2
Daca dam factor comun 1/Q, va rezulta ca:
dCTM/dQ = (CM-CTM):Q
In aceste conditii:
daca CM<CTM, diferenta (CM-CTM) este negativa si CTM scade;
daca CM>CTM, diferenta (CM-CTM) este pozitiva si CTM creste;
daca CM=CTM, diferenta (CM-CTM) este zero si CTM este constant.
Tabelul de mai jos va va ajuta sa intelegeti mai bine modul de determinare a costurilor si relatia dintre ele.
Tab.6.2. Costurile de productie si relatia dintre ele
|
Q |
CF |
CV |
CT |
CM |
CTM |
CFM |
CVM |
Grafic, costurile din tabelul anterior arata astfel:
 Graf.
6.13. Relatia costuri medii - costul marginal
Graf.
6.13. Relatia costuri medii - costul marginal
![]() Legenda: costul mediu
Legenda: costul mediu
![]() costul
variabil mediu
costul
variabil mediu
![]() costul
marginal
costul
marginal
![]() costul
fix mediu
costul
fix mediu
Asa cum puteti observa din tabel si din grafic, pana la un nivel al productiei de 5 bucati costul marginal este sub costul mediu, astfel ca acesta din urma scade. Cand productia atinge cinci unitati cele doua costuri se egalizeaza si CTM este minim, iar dincolo de acest nivel costul marginal depaseste costul mediu, iar costul mediu creste.
b) Costul productiei pe termen lung
B1) CTM pe termen lung - introducere
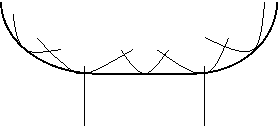
Dupa cum am vazut in prima parte a acestui capitol, pe termen lung se multiplica semnificativ posibilitatile de combinare a factorilor de productie in scopul maximizarii eficientei economice deoarece toti factorii de productie sunt variabili. Din acelasi motiv, distinctia intre costurile fixe si cele variabile dispare, toate costurile fiind acum variabile. Sa sintetizam in continuare tot ceea ce am invatat pana acum. In timp, dupa cum ne sugereaza optimul producatorului (vezi graf.6.7.), firma poate sa-si minimizeze consumurile pe unitate de produs pentru fiecare nivel al productiei pe care il realizeaza. Cu alte cuvinte, prin ajustari succesive si prin substituirea continua a factorilor de productie mai scumpi cu factori mai ieftini, firma reuseste sa atinga, pentru fiecare nivel de productie, minimul costului mediu pe termen scurt. De aceea, curba costului mediu pe termen lung apare ca o "invelitoare" a punctelor de minim ale costului mediu pe termen scurt, astfel:
CTMTL ![]()
![]()

![]()
Zona I Zona II Zona III
![]()
Q
In evolutia costului mediu pe termen lung apare legea randamentelor de scara descrescatoare care, asa cum cunoasteti deja, exprima legatura dintre ritmul de crestere a productiei si cel al cresterii consumului de factori de productie. In consecinta, graficul costului mediu pe termen lung evidentiaza existenta a trei etape in procesul de expansiune a firmei:
zona I este zona randamentelor de scara crescatoare, sau a economiilor de scara;
zona II este zona randamentelor de scara constante;
zona III este cea a randamentelor de scara descrescatoare sau a dezeconomiilor de scara;
Printre cele mai importante explicatii ale economiilor de scara se numara:
i) Costurile facute o singura data. Un exemplu il constituie cheltuielile cu cerecetarea pentru a scoate pe piata o noua generatie de calculatoare sau cele cu reclama pentru lansarea unui nou produs.
ii) Specializarea lucratorilor si utilajelor. Productia pe scara larga permite segmentarea muncii pe operatiuni foarte simple care pot fi executate automat; in plus va este deja cunoscut faptul ca specializarea lucratorilor conduce la cresterea eficientei lor.
iii) Geometria. De exemplu, stiati din scoala generala ca volumul creste mai repede decat suprafata, deci firma care fabrica apa grea reduce cheltuielile de depozitare extinzandu-si suprafata.
iv) Cauze financiare. Este evident ca accesul la sursele de finatare externe firmei este mai ieftin pentru marile corporatii comparativ cu micile firme.
Dezeconomiile de scara se explica in general prin aparitia problemelor de comunicare in cadrul firmei. Din cauza dimensiunilor mari, exista probleme in coordonarea eficienta a operatiunilor din cadrul firmei. Intr-o firma mica intreprinzatorul este strans legat de productie si el este cel care adopta atat deciziile strategice, cat si pe cele curente. In firmele mari apare o indepartare a managerilor de productie si o structura organizatorica ce ingreuneaza procesul decizional. Din cauza unei "birocratii" interne exista posibilitatea ca flexibilitatea firmei la cerintele pietei sa scada. La problemele de comunicare se adauga uneori si alienarea salariatilor, tendinta lor de a amana sau neglija indeplinirea obligatiilor ce le revin atunci cand se simt mai putin supravegehati. Toate aceste cauze conduc la cresterea costului mediu pe termen lung.
Desigur ca toate firmele urmaresc sa ajunga in timp in zona a doua, a randamentelor constante, deoarece costul mediu este minim, iar profitul maxim, sau in cel mai rau caz pierderile sunt minime. Forma costului mediu pe termen lung dintr-un anumit sector de activitate este hotaratoare pentru dimensiunea firmelor din acel sector si pentru concurenta de pe piata respectiva. In domeniile in care costul mediu pe termen lung incepe sa creasca la o productie relativ mica, firmele mari nu sunt competitive in raport cu intreprinderile mici. Daca, dimpotriva, costul incepe sa creasa la productii mari si firmele din acel domeniu vor avea mari dimensiuni. Evident, daca zona a doua este foarte extinsa, pe piata pot sa coexiste firme mici si firme mari, fara ca vreuna dintre ele sa aiba avantaje legate de cost.
B2) Costurile marginale si costurile medii pe termen lung
Pe termen lung firma are posibilitatea sa-si diminueze costurile prin modificarea tuturor factorilor de productie consumati. Cunoastem ca pentru un nivel dat al productiei, costul este minim atunci cand linia izocostului (care reflecta constrangerile bugetare) este tangenta la curba de izoproductie (care reflecta constrangerile tehnologice). Altfel spus, firma isi stabileste nivelul dorit de productie si apoi alege cea mai ieftina combinatie de factori de productie cu care sa-l poata realiza. Atunci cand costul este minim, are loc relatia: RmS=ΔK/ΔL=WmgL/WmgK=Pl/Pk. Sa presupunem ca firma porneste de la o situatie marcata de punctul A, de forma:
Graf. 1.:Optimul producatorului pe termen scurt si pe termen lung

Se poate oserva ca productia Q1 se obtine cu un pret mai mare in A decat in B, ceea ce inseamna ca actiunea legii randamentelor marginale neproportionale impune la un moment dat modificarea ambilor factori de productie (deplasarea in B).
Cantitatea de factori de productie aleasa de firma pentru minimizarea costului, dat fiind nivelul dorit al output-ului, depinde in principal de trei factori: pretul inputurilor si cantitatea de output. Prin urmare putem scrie ca: L=L(Pl, Pk, Q) si K=K(Pl, Pk, Q). Aceste functii poarta numele de cereri derivate de factori sau functii ale cererii conditionate de factori si exprima alegerea de factori de productie care minimizeaza costul pentru un nivel dat al productiei. Altfel spus, cele doua functii raspund la intrebarea: cat de mult ar trebui sa utilizeze firma din fiecare factor daca doreste sa produca otput-ul la cel mai mic cost. Functia costului pe termen lung, tinand cont de cererile derivate, poate fi scrisa ca: CT(Q)=PlL(Pl, Pk,Q)+PkK(Pl, Pk,Q), ecuatie care arata ca minimul costului este acel nivel al costului antrenat de alegerile de factori de productie minimizatoare de cost. Daca preturile factorilor de productie sunt fixe, putem scrie cererile derivate ca: L=L(Q) si K=K(Q). Cum functia costului pe termen scurt in aceste conditii este: CTs=PlLs(Q,K)+PkK si depinde doar de Q inseamna ca putem scrie costul pe termen lung ca: CT(Q)=CTs(Q,K(Q)), intrucat factorul capital devine variabil. Ultima ecuatie arata ca costul minim cand toti factorii sunt variabili este chiar costul minim cand factorul capital este fixat la acel nivel care minimizeaza costul pe termen lung. Cererea derivata de factor munca pe termen lung este acea cerere pe termen scurt pe care firma ar fi facut-o daca ar fi avut un nivel K* al capitalului care minimizeaza costul pe termen lung. Daca impartim ambii membrii ai ecuatiei la Q, obtinem o egalitate intre costurile medii pe termen scurt si pe termen lung. Ultima relatie este foarte importanta pentru ca ea conduce la concluzia ca exista un punct pe termen lung in care costul pe termen lung este egal cu cel pe termen scurt. Cum factorul capital care minimizeaza costul pe termen lung difera de la un nivel al productiei la altul, inseamna ca vom avea o multime de puncte in care costurile succesive pe termen scurt, corespunzatoare unui nivel dat al capitalului, sunt egale cu costul pe termen lung. Daca putem construi o infinitate de curbe de costuri pe termen scurt, costul mediu pe termen lung se va obtine unind alegerile minimizatoare de costuri pe termen scurt, ceea ce inseamna ca curba costului mediu pe termen lung este "infasuratoarea" curbelor costurilor medii pe termen scurt. La aceeasi concluzie putem ajunge mai usor grafic. Sa presupunem ca o firma poate produce Q1 atat in conditiile date de curba costului CTM1, cat si in cele descrise de CTM2. Se observa ca daca firma are la dispozitie doar 2 posibilitati de largire a capitalului, ea va alege CTM1, nu isi va mari dimensiunea, iar punctul A va fi in acest caz pe curba CTM pe termen lung. Daca insa ea mai are la dispozitie un plan CTM3, se observa ca punctul B corespunde unui cost mai mic, ceea ce inseamna ca firma se va extinde pe CTM3, iar B va fi pe curba CTM pe termen lung (gr.1). Observati ca pe curba CTM pe termen lung nu se afla neaparat punctele de minim ale costurilor pe termen scurt, intrucat ele nu mai reflecta maximul de eficienta, pentru ca tot timpul va exista o combinatie de factori pe termen lung la un cost mai mic decat minimul pe teremen scurt; explicatia acestui fapt este existenta randamentelor de scara.
Cunoscand acum conceptul de cost pe termen lung, putem masura economiile de scara cu ajutorul indicelui economiilor de scara (IES), determinat ca: IES=1-Ec, in care Ec este elasticitatea costurilor in raport de productie, determinata astfel: Ec=(ΔCT/CT)/( ΔQ/Q). Cand Ec>1, costurile cresc mai repede decat productia si vom avea randamente de scara descrescatoare si indice negativ (dezeconomii de scara), cand Ec<1, randamentele sunt crescatoare, indicele este pozitiv si semnifica economii de scala, iar cand Ec=1 avem randamente constante, iar indicele este zero.
Cum arata insa costul marginal pe
termen lung? Intuitiv, curba costului marginal pe termen lung va uni punctele
care reprezinta costul marginal pe termen scurt. Aceasta deoarece
fiecarei productii pe termen scurt aleasa ii va corespunde atat
un CTM, cat si un cost marginal, implicit acelor productii pentru
care costul pe termen scurt este egal cu cel pe termen lung. De exemplu,
daca o firma ar avea la dispozitie numai trei
posibilitati de extindere carora le corespunde CTM1, CTM2
si CTM3, costul marginal ar fi: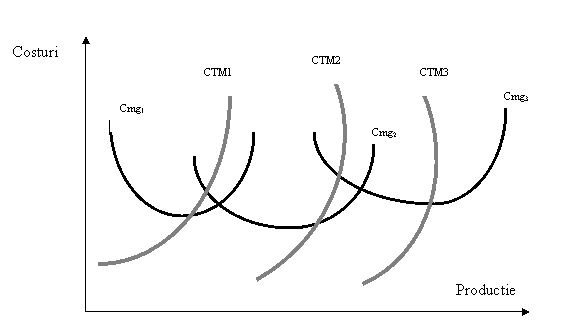
Graf. 2. Extinderea firmei pe termen lung
Daca firma are o infinitate de posibilitati de a se
extinde, atunci costul marginal va arata astfel: 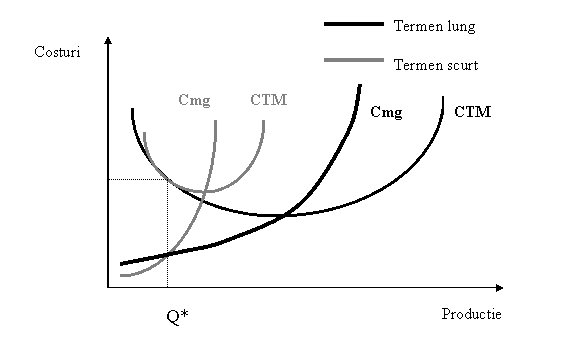
Graf. 3. Relatia dintre costurile pe termen scurt si costurile pe termen lung
Pentru un nivel de productie Q*, costul marginal pe termen lung trebuie sa fie egal cu costul marginal pe termen scurt.
3. 4. Curba de experienta si randamentele de scara
Din discutia de pana in acest punct ar putea sa reiasa ca numai firmele mari se bucura de economii de scara, concluzie care ar veni sa contrazica realitatea ca in multe domenii coexista firme de toate dimensiunile. Cele mici nu ar putea rezista daca ar avea costuri semnificativ mai mari decat firmele mari, pentru aceleasi tipuri de produse, ceea ce conduce la ideea ca si aceste firme experimenteaza cheltuieli mai mici pe termen lung. Explicatia acestora nu se afla insa in economile de scara, ci in capacitatea salariatilor si managerilor de a castiga experienta si a asimila noile informatii si tehnologii.
Curba de experienta, numita si curba de invatare sau functia progresului, descrie relatia dintre cantitatea de input consumata pe unitate de produs si productia cumulativa realizata de firma. Productia cumulativa se refera la cantitatea produsa in timp, nu la nivelul curent al productiei. De exemplu, o firma a produs de-a lungul a patru ani 500, 500, 1000 si respectiv 2000 de piese, ceea ce inseamna ca productia cumulativa este 4000, pe cand cea curenta este 2000. Daca initial aceasta firma consuma 4 ore pentru o unitate de produs, apoi 3,2 ore, iar pentru ultimele 2000 consuma doar 2,2 ore, curba de experienta ar arata astfel:
Timp de munca

Graf. 5. Curba de experienta
Teoria efectului de experienta, mentionata pentru prima data de T.P. Wright in 1936, arata ca pentru orice dublare cumulativa a productiei intr-o anumita ramura, costul total mediu, masurat in unitati monetare constante, scade cu un procent constant. Acest procent a fost evaluat empiric la 3 - 30%, in functie de domeniul de activitate. De exemplu, pentru industria aeronautica el este de cca. 15%.
Cele mai importante explicatii ale efectului de experienta sunt:
efectul de invatare, conform caruia repetarea unei sarcini conduce la scurtarea perioadei de timp necesare pentru realizarea sa, deci la reducerea costului; el este valabil la fel de bine pentru muncitori si pentru manageri; managerii, in plus, invata sa organizeze mai bine fluxul productiei, scurtand perioadele de timp necesare unei operatii sau/si dintre diferitele operatii;
inovatia si substituirea muncii cu capitalul; acumularea de experienta permite imbunatatirea produsului, incepand cu designul si terminand cu inlocuirea unor componente cu altele mai ieftine sau chiar a tehnologiei. Inginerii invata si ei pe parcursul realizarii unui produs si inventeaza noi componente sau noi instrumente de munca, care permit substituirea mai usoara a muncii cu capitalul; De exemplu, la inceputul anilor *70, un televizor color avea peste 5000 de componente, pe cand in prezent el are cca. 500 de componente;
ofertantii de materii prime, furnizorii, "invata" la randul lor necesarul mediu de materii prime al firmei, motiv pentru care firma poate beneficia de reduceri din partea acestora.
Procesul de invatare determina deplasarea in jos a curbei CTM pe termen lung; grafic diferenta dintre randamentele de scara si efectul de invatare este mai evident, astfel:
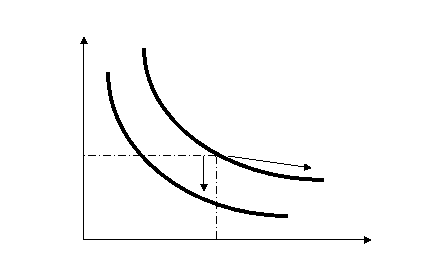
Graf. 6. Curba de experienta si randamentele de scara
Daca economia face distinctie intre randamentele de scara si curba de invatare, adesea in management cel doua sunt incluse sub denumirea larga de curba de experienta, care nu se mai restrange doar la procesul de invatare. Existenta curbei de experienta a condus in practica la fundamentarea strategiilor concurentiale numite strategiile costurilor sau strategii de volum, ale caror obiectiv este minimizarea costurilor.
III. Profitul si incasarile intreprinderii
Conform definitiei,profitul total poate fi scris astfel :
![]()
unde : ![]() =profitul,VT=venitul
total si CT=costul total.
=profitul,VT=venitul
total si CT=costul total.
Venitul total sau cifra de afaceri, depinde de cantitatea vanduta,astfel avem :
![]() ;Q=cantitatea produsa .Venitul total se obtine
prin inmultirea pretului de vanzare al bunului final (P) cu
cantitatea vanduta :
;Q=cantitatea produsa .Venitul total se obtine
prin inmultirea pretului de vanzare al bunului final (P) cu
cantitatea vanduta :![]()
Deoarece atat costul de productie, cat
si incasarile firmei depind de cantitatea vanduta, este normal
ca si profitul sa depinda la randul sau de cantitatea
vanduta, ![]() .
.
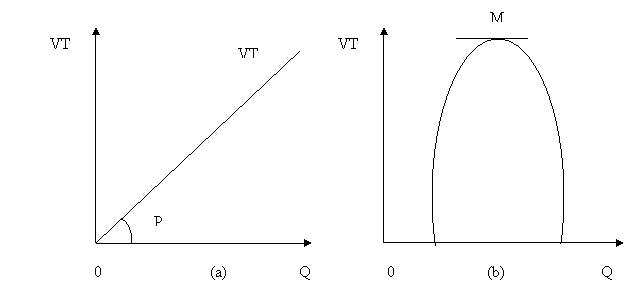
Venitul total este reprezentat in graficul de mai jos. In partea stanga (a), presupunem ca pretul este constant, adica el nu depinde de cantitatea vanduta. In acest caz , panta dreptei venitului total este egala cu pretul de vanzare. In schimb in partea stanga (b), pretul variaza in functie de cantitatea ceruta.
Graficul nr.8.1 Venitul total
Pentru a intelege mai bine, putem lua
ca exemplu urmatoarea functie a cererii :![]() . Ĭn acest caz venitul total poate fi scris
astfel :
. Ĭn acest caz venitul total poate fi scris
astfel :
![]() ;
;
![]() .
.
Ĭn analiza microeconomica, asa cum stim intalnim doua tipuri de incasari : medii (unitare) si marginale. Pe cele medii, le obtinem impartinad venitul total la productie, astfel :
![]()
![]()
![]() ;
; ![]() ;
; ![]() .Din relatia de mai sus observam, ca venitul
mediu este egal cu pretul de vanzare. Intr-adevar venitul
obtinut pentru fiecare unitate vanduta, reprezinta exact
pretul sau de vanzare.
Daca functia cererii firmei , asa cum am spus si mai sus
este de forma
.Din relatia de mai sus observam, ca venitul
mediu este egal cu pretul de vanzare. Intr-adevar venitul
obtinut pentru fiecare unitate vanduta, reprezinta exact
pretul sau de vanzare.
Daca functia cererii firmei , asa cum am spus si mai sus
este de forma ![]() ,venitul mediu este :
,venitul mediu este :![]() .
.
Venitul mediu ,sau mai exact functia
venitului mediu este identica cu functia cereri firmei, pentru
ca, asa cum stim cererea ne arata ca intre cantitatea
ceruta si pret, exista o relatie invers
proportionala. In tabelul de mai jos, putem
observa ca venitul mediu este egal cu pretul, iar functia
cererii are urmatoarea forma :![]()
Tabelul 8.1. Pretul, incasarea medie si incasarea marginala
|
Cantitatea ceruta |
Pretul |
Venitul total |
Venitul mediu |
Venitul marginal |
Ĭncasarea marginala sau venitul
marginal reprezinta un concept cheie in teoria microeconomica, care
trebuie sa fie foarte bine inteles. Venitul marginal ne arata
variatia venitului total ca urmare a cresterii productiei sau a
cantitatii vandute cu o unitate, astfel :![]() .Daca, productia se modifica foarte
putin, venitul marginal poate fi scris ,ca fiind derivata venitului total
in raport cu productia, astfel:
.Daca, productia se modifica foarte
putin, venitul marginal poate fi scris ,ca fiind derivata venitului total
in raport cu productia, astfel:![]() . In tabelul de mai sus, observam ca la o crestere
a cantitatii cerute de la 3 la 2, venitul marginal este :
. In tabelul de mai sus, observam ca la o crestere
a cantitatii cerute de la 3 la 2, venitul marginal este : ![]() .Grafic venitul marginal poate fi reprezentat astfel :
.Grafic venitul marginal poate fi reprezentat astfel :
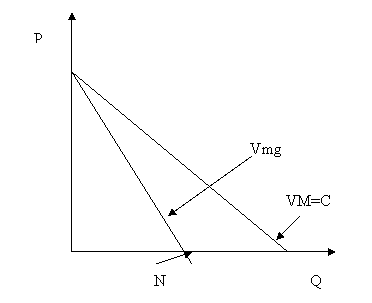
Graficul nr.8.2. Curba cererii si venitul marginal
Expresia VM=C (cererea), ne arata ca, venitul mediu este identic cu cererea. Venitul marginal prezinta urmatoarele caracteristici:
Curba venitului mediu si a venitului marginal, inregistreaza aceeasi valoare in origine : a.
Pentru a verifica acest lucru putem sa plecam , de la datele din tabelul de mai sus :
![]() (functia cererii);
(functia cererii);
![]() ;
;
pentru Q=0, VM=Vmg=24.
Pentru o anumita cantitate vanduta venitul marginal se anuleaza (in exemplul nostru pentru Q=6unitati), apoi devine negativ. Cand cantitatea vanduta trece de la 5 unitati la 6, venitul total creste cu 2 unitati (72-70), iar venitul marginal este pozitiv , deoarece panta curbei venitului total este pozitiva. Daca vanzarile cresc de la 6 unitati la 7, venitul total scade, iar venitul marginal este negativ ; panta curbei venitului total este negativa, dupa punctul M, din graficul nr.1 (b). In acest punct (M), venitul total este maxim. Panta in punctul M, este nula si prin urmare venitul marginal este si el la fel. Punctul M din graficul nr.1(b) corespunde punctului N, din graficul de mai sus.
Putem defini functia venitului
marginal , plecand de la functia cererii , care poate fi scrisa
astfel :![]() .Aceasta relatie, ne arata ca, cantitatea
ceruta depinde de pret (asa cum am vazut in tabelul nr.1).
Inversul acestei functii este :
.Aceasta relatie, ne arata ca, cantitatea
ceruta depinde de pret (asa cum am vazut in tabelul nr.1).
Inversul acestei functii este :![]() cu
cu ![]() : pretul variaza in sens invers cu cantitatea
ceruta. Stim ca
: pretul variaza in sens invers cu cantitatea
ceruta. Stim ca ![]() ; tinand cont de inversul functiei cererii putem
sa scriem venitul total astfel :
; tinand cont de inversul functiei cererii putem
sa scriem venitul total astfel :![]() , iar venitul marginal (plecam de la ipoteza ca, productia variaza foarte
putin) :
, iar venitul marginal (plecam de la ipoteza ca, productia variaza foarte
putin) :
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
Pentru ca ![]() , atunci
, atunci ![]() .Deoarece pretul variaza in functie de
cantitatea ceruta, venitul marginal este mai mic decat pretul. Acest
rezultat are la baza doua
argumente.
.Deoarece pretul variaza in functie de
cantitatea ceruta, venitul marginal este mai mic decat pretul. Acest
rezultat are la baza doua
argumente.
Primul argument se refera la o observatie curenta : pentru a vinde mai mult , firma in cauza trebuie sa scada pretul. Al doilea argument este mult mai important : pentru a vinde o unitate suplimentara, firma va fi obligata sa vanda intreaga cantitate la acelasi pret, mai mic. Consideram datele urmatoare :
|
Q |
P |
VT |
Vmg |
Pentru a vinde doua unitati din
bunul X, o firma trebuie sa reduca pretul de la 100 um la
90 um. Ĭn acest caz ,firma va pierde 10 um pentru fiecare unitate
vanduta. Venitul marginal va fi egal cu : um, fiind mai mic decat pretul de vanzare (90 um).
um, fiind mai mic decat pretul de vanzare (90 um).
Corelatia dintre elasticitatea cererii si venitul firmei, a fost prezentat intr-un capitol anterior si din acest motiv nu o sa mai insistam in aceasta parte a lectiei ; urmand sa discutam acum despre ceea ce urmareste orice firma, maximizarea profitului sau.
8.2. Maximizarea profitului total
In analiza profitului vom porni de la urmatoarea ipoteza : firma actioneaza pe o piata concurentiala iar preturile factorilor de productie si output-urilor sunt considerate date (firma este primitoare de pret ).
Costul total al firmei poate fi scris
astfel :CT=![]() unde Pi
ne arata pretul unitar al factorului i. In cazul in firma dispune de
doi factori de productie(L,K), profitului sau este egal cu:
unde Pi
ne arata pretul unitar al factorului i. In cazul in firma dispune de
doi factori de productie(L,K), profitului sau este egal cu:![]() .
.
Vom analiza in cotinuare profitul atat pe termen scurt cat si pe termen lung. Insa trebuie sa ne amintim din lectiile anterioare, ca :
pe termen scurt : avem factori fixi (recuperabili sau nerecuperabili) + factori variabili.
pe termen lung : avem numai factori variabili.
8.2.1 Maximizarea profitului pe termen scurt
Notam factorii de productie cu Lsi K (K este considerat ca fiind un factor de productie fix).Profitul firmei devine in acest caz este:
![]()
Pe baza relatiei de mai sus,putem calcula dreapta izoprofitului :
![]()
panta izoprofitului este ![]() .
.
Izoprofitul
ne arata ansamblul combinatiilor de factori de productie pentru
care profitul rǎmane constant. De exemplu,daca o firma inregistreaza un Π0=1000
um, P=10 um, PL=PK=1, K=90 ;
atunci dreapta izoprofitului este :![]()
Grafic putem reprezenta aceasta dreapta astfel :
![]() Q
Q
109
![]()
0 L
|
Graficul nr. 8.3 .Dreapta izoprofitului |
Pentru a-si maximiza pofitul firma va cauta sa se plaseze pe cea mai inalta dreapta a izoprofitului posibila.
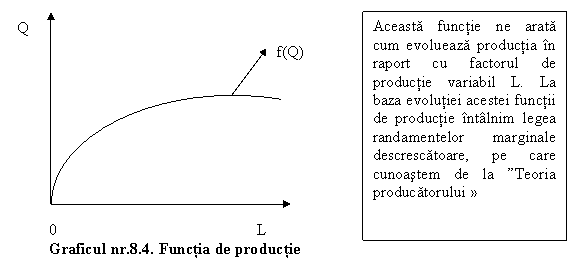
Venitul pe care o firma il poate obtine depinde atat de cantitatile de factori de productie folositi (L,K), cat si de tehnologia de productie,respectiv functia de productie f(L,K).
Grafic functia de productie poate fi reprezentata astfel :
In punctul M, din graficul de mai jos firma poate obtine profitul maxim, iar dreapta izoprofitului devine tangenta la functia de productie.
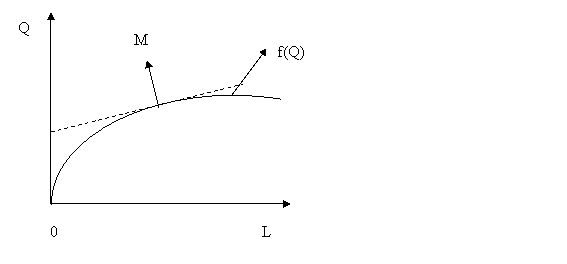
Grafic nr. 8.5. Maximizarea profitului
In acest punct panta functiei de productie (productivitatea marginala a muncii) este egala cu panta izoprofitului :
![]()
Conform relatiei de mai sus, pretul factorului variabil L,
este egal cu produsul dintre pretul de vanzare al bunului final si
productivitatea marginala in raport cu acest factor. Daca ![]() ,putem intalni urmatoarea situatie (daca
plecam de la modificarea absoluta a venitului total si a
costului):
,putem intalni urmatoarea situatie (daca
plecam de la modificarea absoluta a venitului total si a
costului):
![]() =
=![]() ;
;
![]() cu PL=constant
cu PL=constant
In aceasta situatie, ![]() ;
;
![]() .
.
Prin urmare avem :
Deci, in aceasta situatie profitul nu
poate fi maxim, el poate sa cresca sau sa scada. Π este max, atunci cand ![]()
![]()
![]()
 A'
A'
![]() M B'
M B'
B
![]() N
N
A
![]()
0 L'' L' L
Grafic nr. 8.6. Profitul maxim cand panta izoprofitului se modifica
8.2.2 Maximizarea profitului pe termen lung
Pe termen lung obiectivul firmei este maximizarea profitului ca si pe termen scurt, numai ca in acest caz vom pune urmatoarele conditii (toti factorii de productie sunt variabili):
![]()
![]()
![]()
Vom avea deci, doua ecuatii cu doua necunoscute. Rezolvand sistemul obtinem :L(P ;PL;PK) K(P ;PL;PK).
EXEMPLU: Functia
de productie a unei firme este de forma: f(Q)=L2+K2,
P=10 um, PL=1 um iar PK=2um. Care este profitul optim al firmei pe
termen lung ? Deoarece trebuie sa aflam profitul
firmei pe termen lung, vom pune urmatoarele conditii : Putem scrie urmatorul sistem : Rezolvand sistemul vom obtine: Ĭnlocuind pe L,K in functia de
productie, obtinem o productie optima de
![]() ;
; ![]() ;
;![]() ;
;![]() .
.![]() ;
; ![]()
![]() iar
iar ![]() ;
;![]() ;
;![]()
![]()
8.2.3 Maximizarea profitului si randamentele de scara
Natura randamentelor de scara
influenteaza foarte mult profitul unei firme care
actioneaza pe o piata concurentiala. Productia optima a unei firme care-i maximizeaza profitul este
data de urmatoarea functie :f(L,K)=Q ![]()
Daca presupunem ca functia de productie a acestei firme corespunde unor randamentele de scara constante pentru oricare ar fi Q ,avem:
![]() ;
;
![]()
In consecinta: daca randamentele de scara sunt constante, firma poate obtine un profit mai mare decat in situatia initiala. Deci in situatia initiala firma nu a obtinut un profit maxim asa cum am spus mai sus, prin urmare intalnim o CONTRADICTIE.
![]() Profitul initial poate fi optim,
numai daca
Profitul initial poate fi optim,
numai daca ![]()
![]()
Deci pe termen lung, profitul unei firme cu randamente de scara constante este nul
Am putea spune ca acest lucru este absurd. Dar sa ne gandim la ce se poate intampla in situatia in care, o firma mareste in mod continuu cantitatile de factori de productie utilizate, pentru a-si maximiza profitul :
apar randamente de scara descrescatore (firma in cauza ar deveni foarte mare si n-ar mai putea functiona in mod eficient) ;
eliminarea concurentei de pe piatǎ (datoritǎ cresterii dimensiunilor firmei, ea ar incepe sǎ domine piata, ceea ce ar determina formarea unui monopol);
scǎderea profitului (dacǎ o firma inregistreazǎ profit in conditiile unor randamente de scarǎ constante ;toate celelate firme care au acces la aceasta tehnologie vor fi profitabile. Daca una dintre firme isi mǎreste productia firmele concurente vor face acelasi lucru, ceea ce va duce in final la scǎderea pretului de vanzare datoritǎ cresterii ofertei.
3. Profitul economic fata in fata cu profitul contabil
Inainte de a defini profitul economic, respectiv cel contabil, trebuie sa ne aducem aminte semnificatia costului explicit, respectiv implicit, care v-a fost prezentat in capitolul 6. Asa cum stim pentru contabili, cea mai mare importanta o are costul explicit, care ne arata cheltuielile firmei cu achizitionarea sau inchirierea factorilor de care are nevoie. Contabilii evalueaza aceste cheltuieli la valoarea lor trecuta, pentru a calcula ce datoreaza firma diferitilor agenti economici. Pentru economisti, costul implicit are cea mai mare relevanta. Acesta ne arata valoarea factorilor de productie proprii, pe care intreprinderea ii foloseste in procesul de productie.
Economisti calculeaza profitul economic al unei intreprinderi ca diferenta intre incasarile totale si costul de oportunitate.
![]() Costul de oportunitate=costul explicit+costul implicit
Costul de oportunitate=costul explicit+costul implicit
cea mai buna alternativa de valorificare a banilor
Π economic=VT-costul de oportunitate
Atunci cand o firma decide, sa-si diversifice productia, trebuie sa ia in calcul nu numai costul efectiv, cat si veniturile pe care le-ar fi incasat, daca de exemplu nu-si diversifica productia, ci numai crestea volumul productiei sale. Ea va opta pentru diversificarea productiei, numai daca veniturile prognozate sunt mai mari decat cheltuielile aferente, si in plus aceste venituri sunt superioare oricarei alte alternative de valorificare a banilor.
Contabilii calculeaza profitul contabil al unei intreprinderi,ca diferenta intre incasarile totale si costurile explicite.
Π contabil=VT-costurile explicite
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 9374
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2025 . All rights reserved