| CATEGORII DOCUMENTE |
| Agricultura | Asigurari | Comert | Confectii | Contabilitate | Contracte | Economie |
| Transporturi | Turism | Zootehnie |
REGRESIA SIMPLA
Studiem, pentru inceput, cel mai simplu model econometric: o variabila endogena reprezinta evolutia fenomenului considerat si aceasta evolutie este explicata printr-o singura variabila exogena.
In cadrul capitolului este prezentata metoda de estimare a parametrilor care intervin intr-un model econometric, se vor examina proprietatile estimatorilor obtinuti si se vor generaliza rezultatele analizei pentru modele mai complexe. Intr-o prima parte se va trata obtinerea estimatorilor parametrilor modelului si proprietatilor lor, iar intr-o a doua parte se da o interpretarea geometrica a metodei utilizate, determinarea intervalelor de incredere referitoare la parametri si previziunea care poate fi facuta cu un astfel de model.
1. Modelul liniar al regresiei simple
Consideram modelul:
(1)
![]() , t=1, 2, ,T
, t=1, 2, ,T
in care: Y reprezinta o variabila endogena;
X o variabila exogena;
e o variabila aleatoare ale carei caracteristici vor fi precizate prin ipoteze.
Se dispune de T observatii asupra lui Y si X, adica T cupluri (xt, yt) care sunt realizari ale lui X si Y. a si b sunt parametri reali necunoscuti pe care dorim sa-i estimam cu ajutorul observatiilor (xt, yt) cunoscute.
Ipoteze fundamentale
Pentru a putea obtine rezultatele enuntate la inceput, vom simplifica lucrurile impunind o serie de ipoteze restrictive asupra modelului. Ulterior, in alte capitole, se vor relaxa aceste restrictii, discutind implicatiile abandonarii unora din aceste ipoteze asupra calitatii estimatorilor.
I1:
xt si yt sunt marimi numerice observate fara eroare;
X -variabila explicativa se considera data autonom in model;
Y -variabila endogena este o variabila aleatoare, prin intermediul lui e
I2:
a)- e urmeaza o lege de distributie independenta de timp, adica media si dispersia lui e nu depind de t:
![]()
![]() , cantitate finita,
, cantitate finita, ![]() .
.
Observatie:
S-au
folosit aici, pentru medie si dispersie, notatiile ![]() , respectiv
, respectiv
![]() , provenind
de la "speranta matematica" si "varianta" unei variabile aleatoare. Se
presupune ca studentii au cunostinte elementare despre teoria probabilitatilor
si statistica matematica. Altfel, ele trebuie revazute!
, provenind
de la "speranta matematica" si "varianta" unei variabile aleatoare. Se
presupune ca studentii au cunostinte elementare despre teoria probabilitatilor
si statistica matematica. Altfel, ele trebuie revazute!
b)- Realizarile lui e sunt independente de realizarile lui X in cursul timpului. Aceasta este ipoteza de homoscedasticitate. In caz contrar, exista heteroscedasticitate.
c)- Independenta erorilor (se va vedea pe parcurs ca variabila
aleatoare e reprezinta "erori" sau
"reziduuri"). Doua erori relative la doua observatii diferite t si t'
sunt independente intre ele, insemnind ca au covarianta nula: ![]() , ceea ce implica
, ceea ce implica ![]() .
.
Prin
definitie, cov(![]()
![]() si tinind
cont de a) rezulta implicatia.
si tinind
cont de a) rezulta implicatia.
d)- Presupunem ca e urmeaza o lege de
repartitie normala , cu media 0 si dispersia ![]() , ceea ce
poate fi scris astfel:
, ceea ce
poate fi scris astfel: ![]() .
.
I3:
Primele momente empirice ale variabilei X, pentru T foarte mare, sunt finite:
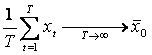 (media empirica).
(media empirica).
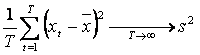 (varianta empirica).
(varianta empirica).
Aceasta ipoteza va fi folosita pentru a preciza proprietatile asimptotice ale estimatorilor parametrilor a si b.
Ipotezele I1, I2, I3 pot parea foarte restrictive. Vom vedea ulterior ce consecinte are abandonarea unora dintre ele asupra proprietatilor estimatorilor lui a si b.
Determinarea estimatorilor parametrilor
prin metoda celor mai mici patrate
Determinarea estimatorilor
parametrilor a si b (notati cu ![]() si
si ![]() ) prin
metoda celor mai mici patrate (MCMMP) se face punand conditia ca suma
patratelor erorilor sa fie minima, adica:
) prin
metoda celor mai mici patrate (MCMMP) se face punand conditia ca suma
patratelor erorilor sa fie minima, adica:
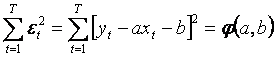
Pentru ca ![]() sa fie minimala, trebuie ca:
sa fie minimala, trebuie ca:
conditii necesare: ![]() ,
, ![]() .
.
conditii suficiente: ![]() ,
, 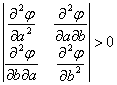 .
.
Calculam derivatele partiale
ale functiei ![]() .
.
![]()
![]()
![]()
![]()
![]()
Atunci, conditiile de ordinul I (necesare) conduc la sistemul de ecuatii:

iar conditiile suficiente (de ordinul II) sunt verificate. Ecuatiile conditii de ordinul I (numite ecuatii normale, cu o justificare geometrica eleganta in partea a II-a), le impartim la T, rezultand:

Din a doua ecuatie avem ![]() si inlocuind in prima ecuatie:
si inlocuind in prima ecuatie:

Am obtinut estimatorii ![]() si
si ![]() ai
parametrilor a si b dati de relatiile:
ai
parametrilor a si b dati de relatiile:
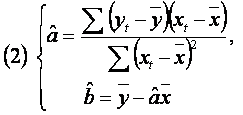
Observatie
![]() este o variabila aleatoare pentru ca e functie
de yt, iar
este o variabila aleatoare pentru ca e functie
de yt, iar ![]() este aleator pentru ca e functie de
este aleator pentru ca e functie de ![]() .
.
Proprietatile estimatorilor
Vom arata ca estimatorii ![]() si
si ![]() obtinuti
prin metoda celor mai mici patrate sunt nedeplasati
si convergenti. In demonstratie vom
tine cont de ipotezele I1, I2, I3. Pentru a
usura demonstrarea proprietatilor enuntate, transformam mai intai expresiile
(2) pentru a le exprima in functie de parametrii a si b. Vom considera
modelul (1)
obtinuti
prin metoda celor mai mici patrate sunt nedeplasati
si convergenti. In demonstratie vom
tine cont de ipotezele I1, I2, I3. Pentru a
usura demonstrarea proprietatilor enuntate, transformam mai intai expresiile
(2) pentru a le exprima in functie de parametrii a si b. Vom considera
modelul (1) ![]() , t=1, 2, ,T, insumam dupa toti t si impartim la T. Rezulta:
, t=1, 2, ,T, insumam dupa toti t si impartim la T. Rezulta:
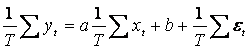 , adica
, adica
![]()
Scadem membru cu membru pe (2) din (1):
![]()
si inlocuim ![]() in expresia lui
in expresia lui ![]() :
:
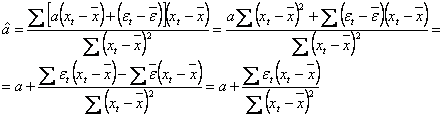
(deoarece ![]() ).
).
Din expresia lui ![]() , avem ca
, avem ca ![]() , adica
, adica ![]() , iar din (2)
, iar din (2)
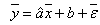 , astfel ca
prin scadere rezulta:
, astfel ca
prin scadere rezulta: ![]() sau
sau ![]() . Am
obtinut ca:
. Am
obtinut ca:
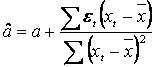
![]()
![]() si
si ![]() sunt estimatori nedeplasati pentru a si b.
Un estimator este nedeplasat daca media estimatorului este chiar parametrul
estimat. Vom aplica operatorul de medie E
in relatiile gasite mai sus.Pentru
comoditate, notam cu wt cantitatea:
sunt estimatori nedeplasati pentru a si b.
Un estimator este nedeplasat daca media estimatorului este chiar parametrul
estimat. Vom aplica operatorul de medie E
in relatiile gasite mai sus.Pentru
comoditate, notam cu wt cantitatea:
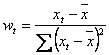 , astfel ca
, astfel ca
![]()
Rezulta:
![]() , pentru ca E(a)=a si E(et
, pentru ca E(a)=a si E(et
![]()
Avem
ca: E(b)=b,  si
si ![]() , deci
, deci ![]()
![]() si
si ![]() sunt estimatori convergenti pentru a si b.
Stiind ca
sunt estimatori convergenti pentru a si b.
Stiind ca ![]() si
si ![]() , este suficient sa aratam ca
, este suficient sa aratam ca ![]() si
si ![]() pentru ca
pentru ca ![]() si
si ![]() sa fie convergenti in probabilitate catre a si b. Calculam varianta
estimatorilor
sa fie convergenti in probabilitate catre a si b. Calculam varianta
estimatorilor ![]() si
si ![]()
Stim ca ![]() , adica
, adica ![]() .
.

Conform
ipotezelor fundamentale, ![]() si
si ![]() , pentru
, pentru ![]() , rezultand:
, rezultand:
![]()
dar  .
.
In final,
dispersia estimatorului ![]() este:
este:
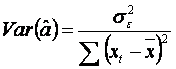 .
.
Conform ipotezei
I3, ![]() si avem ca
si avem ca 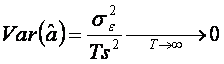 .
.
Am obtinut ca 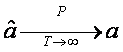 (
(![]() este
convergent in probabilitate catre a).
este
convergent in probabilitate catre a).
Determinam acum
dispersia estimatorului ![]() :
:
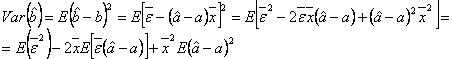
Evaluam, pe rind, fiecare termen:
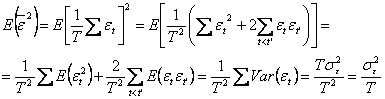
(deoarece ![]() ).
).

dar  ,
,
adica ![]() .
.
Folosind aceste rezultate partiale, se obtine:

Dispersia
estimatorului ![]() este:
este:
![]()

Cum insa ![]() si
si  rezulta ca
rezulta ca ![]() , adica
, adica ![]() (
(![]() converge
in probabilitate catre b) .
converge
in probabilitate catre b) .
Covarianta estimatorilor ![]() si
si ![]()
Calculam acum covarianta estimatorilor pornind de la definitie:
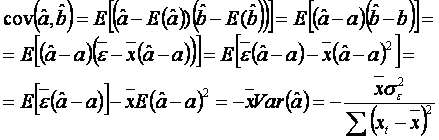
Matricea de varianta si
covarianta a lui ![]() si
si ![]() , notata
, notata ![]() este deci:
este deci:

Se remarca faptul ca ![]() contine pe
contine pe ![]() , adica
varianta lui
, adica
varianta lui ![]() care este necunoscuta. Se pune deci problema
de a obtine o estimatie pentru
care este necunoscuta. Se pune deci problema
de a obtine o estimatie pentru ![]() , adica o
estimatie pentru
, adica o
estimatie pentru ![]() . Notam
aceasta estimatie cu
. Notam
aceasta estimatie cu ![]() .
.
Determinarea unui estimator nedeplasat pentru varianta erorilor
Utilizand estimatorii ![]() si
si ![]() putem
calcula estimatia variabilei endogene yt,
notata
putem
calcula estimatia variabilei endogene yt,
notata ![]() (se mai
numesc si valori ajustate ale variabilei endogene):
(se mai
numesc si valori ajustate ale variabilei endogene): ![]() .
.
Atunci diferenta dintre yt si ![]() este un estimator pentru eroarea
este un estimator pentru eroarea ![]() . Notam
. Notam ![]() . Avem ca
. Avem ca ![]() . Remarca: deoarece
. Remarca: deoarece ![]() si
si ![]() converg in probabilitate catre a si b,
distributia lui
converg in probabilitate catre a si b,
distributia lui ![]() converge in probabilitate catre distributia
lui
converge in probabilitate catre distributia
lui ![]() (distributie normala, conform I2).
(distributie normala, conform I2).
Stim ca ![]() si inlocuind obtinem:
si inlocuind obtinem:
![]()
iar prin ridicare la patrat:
![]()
Insumam dupa t=1,2,,T si impartim la T:
![]()
Dar: 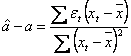 , si
, si
![]()
pentru ca  .
.
Inlocuind, rezulta:
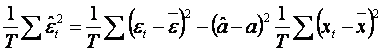
Notam cu ![]() dispersia erorilor fata de media lor si cum ea
este o variabila aleatoare, ii calculam media
dispersia erorilor fata de media lor si cum ea
este o variabila aleatoare, ii calculam media ![]() :
:
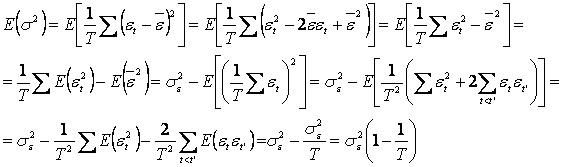
Aplicand acum operatorul de medie in relatia:
![]()
si tinind cont de expresia
variantei estimatorului ![]() , rezulta:
, rezulta:
![]()
Relatia gasita se poate
scrie si astfel: 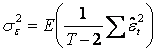 , asa ca,
notand
, asa ca,
notand ![]() , am
obtinut:
, am
obtinut: ![]() , adica
, adica ![]() este un estimator nedeplasat pentru
este un estimator nedeplasat pentru ![]() (varianta erorilor).
(varianta erorilor).
Este de remarcat ca modelul ![]() presupune estimarea a doi parametri (a si b),
iar numitorul lui
presupune estimarea a doi parametri (a si b),
iar numitorul lui ![]() este T-
(T-2) constituie "numarul gradelor de libertate". Vom
reveni ulterior asupra acestei probleme.
este T-
(T-2) constituie "numarul gradelor de libertate". Vom
reveni ulterior asupra acestei probleme.
In concluzie, pentru modelul liniar al regresiei simple, avem estimatorii:

![]()
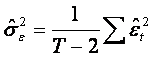
Estimatorul ![]() permite sa dam o estimatie a variantelor si
covariantei parametrilor din model, deci o estimatie a matricei
permite sa dam o estimatie a variantelor si
covariantei parametrilor din model, deci o estimatie a matricei ![]() , notata
, notata ![]() :
:
 , unde:
, unde:
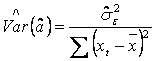 ,
,
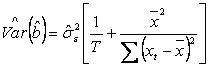 ,
,
![]() .
.
Interpretarea geometrica a metodei celor mai mici patrate
Am determinat estimatorii ![]() si
si ![]() ai parametrilor modelului utilizand conditia
necesara de existenta a minimului sumei patratelor erorilor
ai parametrilor modelului utilizand conditia
necesara de existenta a minimului sumei patratelor erorilor ![]() . Putem sa
dam o conditie necesara si suficienta pentru ca
. Putem sa
dam o conditie necesara si suficienta pentru ca ![]() sa fie minimala, cu ajutorul unei reprezentari
grafice. Aceasta conditie va consta in egalitatea cu zero a doua produse
scalare care redau ecuatiile normale.
sa fie minimala, cu ajutorul unei reprezentari
grafice. Aceasta conditie va consta in egalitatea cu zero a doua produse
scalare care redau ecuatiile normale.
Modelul ![]() se scrie sub forma matriceala astfel:
se scrie sub forma matriceala astfel: ![]() ,
,
unde:  ,
, 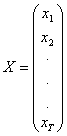 ,
,  ,
, 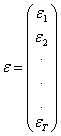 .
.
In spatiul ortonormat ![]() consideram vectorii Y, X, U si e
consideram vectorii Y, X, U si e
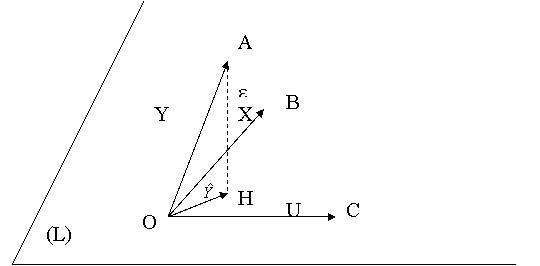

Vectorul 0H=aX+bU apartine planului (L)
determinat de vectorii X si U. Fie 0A=Y, 0B=X, 0C=U, HA=e. Cantitatea ![]() este minimala daca HA este ortogonal pe (L), adica pe X si U. Aceasta conditie
se traduce prin egalitatea cu zero a produsului scalar al vectorilor respectivi:
este minimala daca HA este ortogonal pe (L), adica pe X si U. Aceasta conditie
se traduce prin egalitatea cu zero a produsului scalar al vectorilor respectivi:
![]() , sau
, sau ![]() , adica
, adica 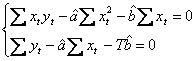 .
.
Am regasit, deci, sistemul de ecuatii normale.
Notam ![]() proiectia pe planul (L) a vectorului Y si cu
proiectia pe planul (L) a vectorului Y si cu ![]() vectorul HA ortogonal la planul (L).
vectorul HA ortogonal la planul (L).
A efectua o regresie a
variabilei Y asupra variabilei X in modelul ![]() revine, deci, la a proiecta vectorul Y pe planul (L) din
revine, deci, la a proiecta vectorul Y pe planul (L) din ![]() determinat de X
determinat de X
Observatie
Consideram
modelul ![]() . O
reprezentare analoga celei dinainte este:
. O
reprezentare analoga celei dinainte este:
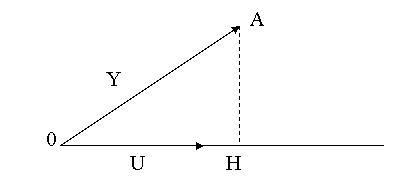

In
scriere matriciala, modelul este ![]() , iar
conform cu reprezentarea grafica, avem relatia OA=OH+HA.
, iar
conform cu reprezentarea grafica, avem relatia OA=OH+HA.
![]() este minimala daca
este minimala daca ![]() (HA
este perpendicular pe 0H), adica
(HA
este perpendicular pe 0H), adica ![]() sau
sau ![]() sau
sau ![]() ,
, ![]() si
si ![]() . Masura
algebrica a proiectiei vectorului Y
pe suportul vectorului U este
. Masura
algebrica a proiectiei vectorului Y
pe suportul vectorului U este ![]() . Vom
utiliza aceasta observatie pentru a exprima ecuatia variantei.
. Vom
utiliza aceasta observatie pentru a exprima ecuatia variantei.
Ecuatia variantei
Reluam reprezentarea geometrica precedenta si notam cu K proiectia lui A pe suportul vectorului U:
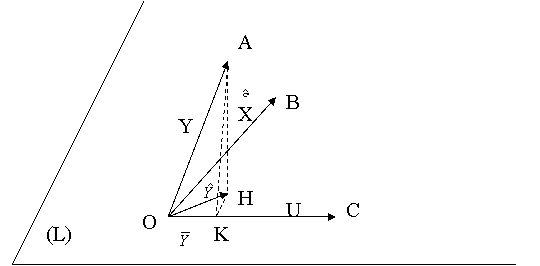

Evident, KH este perpendicular in K pe 0C. In triunghiul AKH, dreptunghic, avem:
![]()
Stim ca ![]() si
si 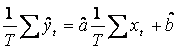 , adica:
, adica: ![]() . Dar si
. Dar si ![]() , rezultand
ca
, rezultand
ca ![]() .
.
Deoarece: AK=0A-0K
(![]() dreptunghic in K)
dreptunghic in K)
HK=0H-0K (![]() dreptunghic
in K),
dreptunghic
in K),
rezulta, folosind (1):
![]()
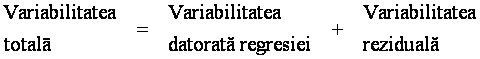
Aceasta este ecuatia variantei. Vom reveni asupra ei cand vom aborda regresia multipla.
3.4. Coeficientul de corelatie liniara
Coeficientul de corelatie liniara intre variabilele X si Y, notat r, se calculeaza cu relatia:

In general, ![]() , unde
, unde ![]() si
si ![]() sunt abaterile standard (radicalul dispersiei)
ale variabilelor X si Y.
sunt abaterile standard (radicalul dispersiei)
ale variabilelor X si Y.
Stim ca estimatorul
parametrului a are expresia 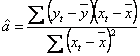 , astfel ca
putem scrie:
, astfel ca
putem scrie:
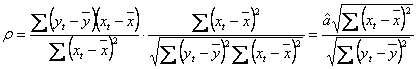 . Am obtinut o expresie a
coeficientului de corelatie in functie de estimator, iar prin ridicare la
patrat:
. Am obtinut o expresie a
coeficientului de corelatie in functie de estimator, iar prin ridicare la
patrat:  .
.
Un calcul imediat arata ca: ![]() .
.
In acelasi timp, ecuatia variantei conduce la: ![]() , de unde:
, de unde: 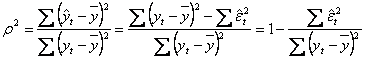 .
.
Pe de alta parte, utilizand
figura geometrica si notand cu α unghiul ![]() , avem
, avem ![]() ,
,  , adica
, adica 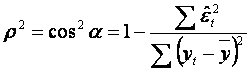 .
.
In mod necesar, ![]() si
si ![]() .
.
Cand ![]() , nu exista
o relatie de tip liniar
, nu exista
o relatie de tip liniar ![]() intre yt
si xt, adica a=0.
intre yt
si xt, adica a=0.
Cand ![]() , yt este legat de xt printr-o relatie de forma
, yt este legat de xt printr-o relatie de forma ![]() .
. ![]() implica a>0, iar
implica a>0, iar ![]() implica a<0.
implica a<0.
Cand relatia dintre yt
si xt nu este stricta,
adica ![]() , atunci r este apropiat de 1, semnul
lui r fiind cel al lui a.
, atunci r este apropiat de 1, semnul
lui r fiind cel al lui a.
3.5. Distributia de probabilitate a estimatorilor
Deoarece erorile et t=1,2,,T au o
distributie normala, de medie zero si dispersie ![]() ,
densitatea de probabilitate a lui et este:
,
densitatea de probabilitate a lui et este:

Cum et si et' sunt independente pentru ![]() ,
densitatea de probabilitate a vectorului aleator (e e eT) va fi egala cu produsul
densitatilor de probabilitate relative la fiecare et
,
densitatea de probabilitate a vectorului aleator (e e eT) va fi egala cu produsul
densitatilor de probabilitate relative la fiecare et
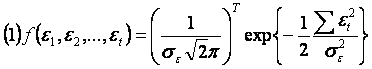
Dar, ![]() si
si
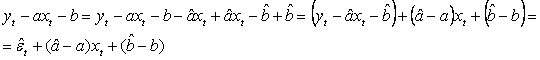 (deoarece
(deoarece ![]() ).
).
Evaluam suma patratelor erorilor:

( ![]() ,
, ![]() pentru ca asa cum arata reprezentarea grafica, vectorul
pentru ca asa cum arata reprezentarea grafica, vectorul ![]() este ortogonal la planul (L), prin urmare este perpendicular pe orice
vector din acel plan, deci si pe X si
U. Produsele scalare cu acesti
vectori vor fi nule, adica:
este ortogonal la planul (L), prin urmare este perpendicular pe orice
vector din acel plan, deci si pe X si
U. Produsele scalare cu acesti
vectori vor fi nule, adica: ![]() si
si ![]() ).
).
Intr-o scriere matriciala:
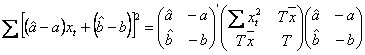
( lasam studentilor placerea de a verifica !).
Inlocuind in (1) fiecare et prin expresiile calculate mai sus, deducem densitatea de probabilitate a vectorului aleator
(y1,y2,,yT):

Tinand cont de matricea de
varianta si covarianta a estimatorilor, ![]() , se arata
usor ca:
, se arata
usor ca: 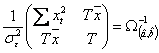 si
si 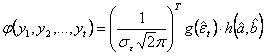 unde
unde ![]() este densitatea de probabilitate a lui
este densitatea de probabilitate a lui ![]() , iar
, iar ![]() cea a lui
cea a lui ![]() .
.
Cu aceste rezultate si facind apel la unele teoreme importante ale statisticii matematice, putem deduce urmatoarele distributii de probabilitate:
Deoarece ![]() , adica
, adica ![]() , variabila
aleatoare definita de raportul
, variabila
aleatoare definita de raportul 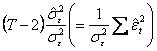 urmeaza o repartitie c2 (hi-patrat)
cu (T-2) grade de libertate.
(Vectorul
urmeaza o repartitie c2 (hi-patrat)
cu (T-2) grade de libertate.
(Vectorul ![]() admite T-2
componente independente nenule
distribuite dupa T-2 legi normale
independente, cu media zero si abatere standard
admite T-2
componente independente nenule
distribuite dupa T-2 legi normale
independente, cu media zero si abatere standard ![]() )
)
Folosind relatile de calcul stabilite anterior, rezulta
ca 
(am utilizat aici
notatiile ![]() si
si ![]() pentru
varianta estimatorului
pentru
varianta estimatorului ![]() , respectiv
pentru estimatia acesteia). Atunci variabila aleatoare definita de raportul
, respectiv
pentru estimatia acesteia). Atunci variabila aleatoare definita de raportul 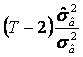 urmeaza tot o repartitie c2
cu (T-2) grade de libertate.
urmeaza tot o repartitie c2
cu (T-2) grade de libertate.
Cuplul ![]() urmeaza o repartitie normala bidimensionala,
astfel ca variabilele aleatoare definite mai jos au repartitiile urmatoare:
urmeaza o repartitie normala bidimensionala,
astfel ca variabilele aleatoare definite mai jos au repartitiile urmatoare:
v
 ;
;
v
 (repartitia Student cu (T-2)
grade de libertate);
(repartitia Student cu (T-2)
grade de libertate);
v
 ;
;
v
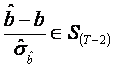 .
.
Expresia 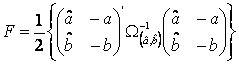 este variabila aleatoare repartizata Fisher-Snedecor,
cu 2 si (T-2) grade de libertate.
este variabila aleatoare repartizata Fisher-Snedecor,
cu 2 si (T-2) grade de libertate.
4. Teste si intervale de incredere
Pentru ca exista tabele cu valorile legilor de probabilitate anterioare, putem determina intervale de incredere pentru parametrii a si b la un nivel de semnificatie a fixat.

![]() este luat din tabela distributiei Student cu (T-2) grade de libertate. Un calcul
simplu conduce la intervalul de incredere pentru parametrul a, de forma:
este luat din tabela distributiei Student cu (T-2) grade de libertate. Un calcul
simplu conduce la intervalul de incredere pentru parametrul a, de forma:
![]()
ceea ce permite afirmatia ca
adevarata valoare a parametrului real a
, se gaseste in intervalul de valori ![]() cu probabilitatea 1-α.
cu probabilitatea 1-α.
Cand se doreste testarea unei valori a0 a parametrului a, este suficient, pentru a accepta aceasta valoare cu riscul a, sa ne asiguram ca:
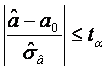
Altfel spus, este suficient
ca a0 sa apartina
intervalului de incredere stabilit: ![]() .
.
De asemenea, ![]() .
.
![]() este ecuatia unei elipse cu centrul in
este ecuatia unei elipse cu centrul in ![]() care defineste astfel o "regiune" de incredere
pentru cuplul
care defineste astfel o "regiune" de incredere
pentru cuplul ![]() la nivelul de semnificatie a
la nivelul de semnificatie a
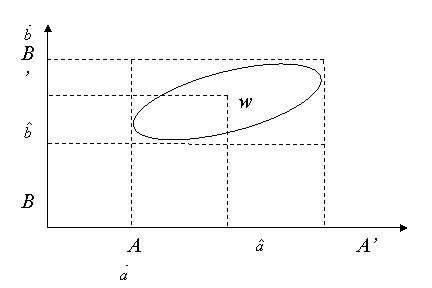

Proiectiile acestei elipse
pe axe determina, de asemenea, doua intervale de incredere pentru a si b,
centrate in ![]() si
si ![]() . Dar, este
important de remarcat ca, nivelul de semnificatie referitor la aceste intervale
nu mai este nivelul a asociat elipsei.
. Dar, este
important de remarcat ca, nivelul de semnificatie referitor la aceste intervale
nu mai este nivelul a asociat elipsei.
Daca se doreste testarea simultana a doua valori a0, b0 alese apriori, este suficient sa inlocuim a si b in expresia F prin a0 si b0.
Daca ![]() se accepta valorile, altfel ele vor fi
respinse. Altfel spus, pentru a accepta cuplul (a0, b0)
la nivelul de semnificatie a este suficient ca punctul M0(a0,b0)
sa apartina elipsei de incredere asociata cuplului (a, b).
se accepta valorile, altfel ele vor fi
respinse. Altfel spus, pentru a accepta cuplul (a0, b0)
la nivelul de semnificatie a este suficient ca punctul M0(a0,b0)
sa apartina elipsei de incredere asociata cuplului (a, b).
Observatii
Expresia ![]() se descompune in doi factori (g si h).
g se exprima doar in functie de
se descompune in doi factori (g si h).
g se exprima doar in functie de ![]() , adica in
functie de yt,
, adica in
functie de yt, ![]() ,
, ![]() ; h nu contine decat pe
; h nu contine decat pe ![]() ,
, ![]() , a si b.
Aceasta arata ca, odata cunoscuta o realizare a cuplului
, a si b.
Aceasta arata ca, odata cunoscuta o realizare a cuplului ![]() , legea de
probabilitate conditionata a lui yt
(data de factorul g) nu depinde decat
de valorile adevarate (dar necunoscute) ale parametrilor a si b. Se zice ca
, legea de
probabilitate conditionata a lui yt
(data de factorul g) nu depinde decat
de valorile adevarate (dar necunoscute) ale parametrilor a si b. Se zice ca ![]() sunt estimatori "exhaustivi" pentru a si b,
adica ei rezuma toata informatia pe care esantionul o poate aduce despre a si b.
sunt estimatori "exhaustivi" pentru a si b,
adica ei rezuma toata informatia pe care esantionul o poate aduce despre a si b.
Cand ipoteza de normalitate asupra erorilor ![]() este realizata, functia de verosimilitate
relativa la esantionul
este realizata, functia de verosimilitate
relativa la esantionul ![]() este chiar functia
este chiar functia ![]() . Pentru
obtinerea de estimatori ai lui a si b prin metoda verosimilitatii maxime,
este suficient sa maximizam expresia
. Pentru
obtinerea de estimatori ai lui a si b prin metoda verosimilitatii maxime,
este suficient sa maximizam expresia ![]() , adica sa
minimizam
, adica sa
minimizam ![]() .
Estimatorii
.
Estimatorii ![]() obtinuti cu metoda celor mai mici patrate
coincid, deci, cu cei obtinuti prin metoda verosimilitatii maxime.
obtinuti cu metoda celor mai mici patrate
coincid, deci, cu cei obtinuti prin metoda verosimilitatii maxime.
Atunci cand ipoteza de normalitate a erorilor nu se
realizeaza, se va arata ca estimatorii ![]() si
si ![]() obtinuti
prin metoda celor mai mici patrate au varianta minima printre toti estimatorii
liniari centrati in a si b (se va da o demonstratie pe cazul
general).
obtinuti
prin metoda celor mai mici patrate au varianta minima printre toti estimatorii
liniari centrati in a si b (se va da o demonstratie pe cazul
general).
5. Previziunea cu modelul liniar
Fie ![]() realizarea variabilei exogene la momentul q. Valoarea previzionata
pentru endogena Y va fi:
realizarea variabilei exogene la momentul q. Valoarea previzionata
pentru endogena Y va fi:
![]()
iar realizarea efectiva a lui Y este:
![]()
Eroarea de previziune se
poate exprima prin variabila aleatoare ![]() .
.
![]()
Se remarca imediat ca ![]() , iar
varianta erorii de previziune este:
, iar
varianta erorii de previziune este:
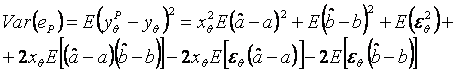
Ultimii doi termeni sunt
nuli (s-a demonstrat anterior!) (e si ![]() , ca si e si
, ca si e si ![]() sunt
necorelati).
sunt
necorelati).
Deci:
![]()
Notam varianta erorii de
previziune cu ![]() si folosind relatiile de calcul anterioare, rezulta:
si folosind relatiile de calcul anterioare, rezulta:

![]() este necunoscut, dar estimat prin
este necunoscut, dar estimat prin ![]() si varianta estimata a erorii de previziune
este:
si varianta estimata a erorii de previziune
este:

Aceasta varianta poate fi
redusa, pe de o parte prin cresterea numarului de observatii (T), iar pe de alta parte, prin alegerea
lui ![]() astfel incat
astfel incat ![]() sa nu fie prea mare (adica facand o previziune
pe termen scurt).
sa nu fie prea mare (adica facand o previziune
pe termen scurt).
Deoarece erorile sunt normal
distribuite, ![]() atunci si
atunci si ![]() si
si ![]() (urmeaza legi normale). Rezulta urmatoarele
distributii de probabilitate pentru variabilele:
(urmeaza legi normale). Rezulta urmatoarele
distributii de probabilitate pentru variabilele:

 urmeaza o lege Student cu T-2 grade de libertate pentru ca
urmeaza o lege Student cu T-2 grade de libertate pentru ca ![]() .
.
In planul (x,y) trasam dreapta de ajustare ![]() . Fie
. Fie ![]() punctul situat pe dreapta de ajustare. Putem
construi, avand P ca centru si
paralel cu axa 0y un interval de
incredere M1M2
la nivelul de semnificatie a
punctul situat pe dreapta de ajustare. Putem
construi, avand P ca centru si
paralel cu axa 0y un interval de
incredere M1M2
la nivelul de semnificatie a
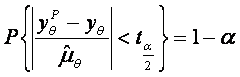
![]() fiind luat din tabela distributiei Student.
Pentru T dat,
fiind luat din tabela distributiei Student.
Pentru T dat, ![]() ca functie de
ca functie de ![]() este minim pentru
este minim pentru ![]() . Punctele M1 si M2 sunt deci situate, cand q variaza, pe doua arce de
curba (vezi figura), care determina astfel regiunea careia ii apartine
. Punctele M1 si M2 sunt deci situate, cand q variaza, pe doua arce de
curba (vezi figura), care determina astfel regiunea careia ii apartine ![]() pentru
pentru ![]() dat, cu o probabilitate egala cu (1-a
dat, cu o probabilitate egala cu (1-a
![]()


Observatii
1.
"O variabila aleatoare t este
distribuita dupa o lege Student cu T-2
grade de libertate daca expresia ![]() este raportul dintre o variabila aleatoare
distribuita
este raportul dintre o variabila aleatoare
distribuita ![]() cu 1 grad de libertate si o alta distribuita
cu 1 grad de libertate si o alta distribuita ![]() cu (T-2)
grade de libertate". Fie
cu (T-2)
grade de libertate". Fie ![]() . Atunci:
. Atunci: 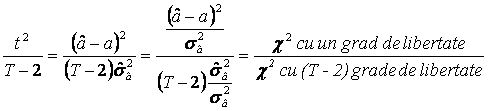 .
.
"O variabila aleatoare F este distribuita dupa o lege Fisher-Snedecor cu n1 si n2
grade de libertate daca expresia ![]() este raportul dintre o variabila aleatoare
distribuita
este raportul dintre o variabila aleatoare
distribuita ![]() cu n1
grade de libertate si o alta distribuita
cu n1
grade de libertate si o alta distribuita ![]() cu n2
grade de libertate".
cu n2
grade de libertate".
Fie  .
.
Atunci:

pentru ca ![]() urmeaza o lege normala bidimensionala.
urmeaza o lege normala bidimensionala.
3.
Jacobianul transformarii permite exprimarea densitatii de probailitate a
vectorului aleator ![]() pornind de la cea a lui
pornind de la cea a lui ![]() . Cand
. Cand ![]() este cunoscuta, pentru a obtine
este cunoscuta, pentru a obtine ![]() , procedam
astfel:
, procedam
astfel:
Inlocuim ![]() prin expresia ei in functie de
prin expresia ei in functie de ![]() ;
;
Inmultim expresia obtinuta cu valoarea absoluta a determinantului:

![]()
4.
Am vazut ca ![]() ,
, ![]() si
si ![]() fiind distribuite normal.
fiind distribuite normal. ![]() este o combinatie liniara de
este o combinatie liniara de ![]() . Deci:
. Deci:
![]()
![]() este distribuita c2 cu 1 grad de
libertate pentru ca este patratul unei variabile aleatoare N(0,1).
este distribuita c2 cu 1 grad de
libertate pentru ca este patratul unei variabile aleatoare N(0,1).
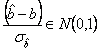
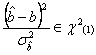
Deoarece
![]() , prin
impartirea la
, prin
impartirea la ![]() , obtinem:
, obtinem:

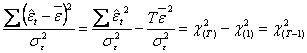
![]()
Rezulta ca:
 .
.
6. Experienta de calcul
Pentru a studia cum variaza cheltuielile de intretinere si reparatii ale unui utilaj agricol in functie de "varsta" utilajului, s-au cules urmatoarele date:
|
Varsta utilajului (xt) -in luni- | ||||||||
|
Cheltuieli anuale de intretinere si reparatii (yt) -in RON- | ||||||||
|
Varsta utilajului (xt) -in luni- | ||||||||
|
Cheltuieli anuale de intretinere si reparatii (yt) -in RON- |
Rezolvare:
Cautam sa estimam parametrii
unei regresii liniare inte variabilele X
si Y, de forma ![]() , presupunind ca sunt indeplinite ipotezele
fundamentale I1,I2,I3.
, presupunind ca sunt indeplinite ipotezele
fundamentale I1,I2,I3.
1. Pentru a calcula estimatorii, se folosesc relatiile de calcul stabilite anterior (in cadrul seminarului se vor prezenta facilitatile de calcul oferite de diferite pachete de programe dedicate). Elementele necesare calculului sunt date in tabelul ce urmeaza:

Pe baza elementelor din tabelul de calcul, se determina:
- 
![]()
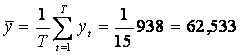
-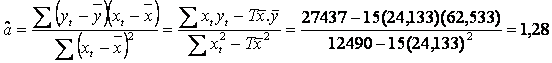 -
- ![]()
- coeficientul de corelatie liniara:
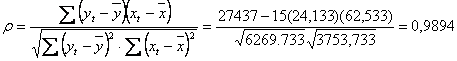
Valoarea apropiata de 1 a coeficientului de corelatie arata ca intre cele doua variabile studiate exista o corelatie liniara.
Observatie: Am vazut ca:

Patratul coeficientului de corelatie liniara este raportul dintre variabilitatea explicata prin model si variabilitatea totala.
- ecuatia de analiza a variantei:
variabilitatea totala = variabilitatea explicata + variabilitatea reziduala
![]()
= 6137,719 + 132,014
In spatiul observatiilor, Y este cu atat mai bine explicat prin modelul liniar, cu cat este mai aproape se planul (L) generat de vectorii X si U (vectorul unitar), deci cu cat variabilitatea reziduala este mai mica fata de variabilitatea empirica totala. Aceasta face ca raportul dintre variabilitatea explicata prin model si variabilitatea totala, adica ρ2, sa fie apropiat de 1.
- estimatiile variantelor reziduurilor si ale estimatorilor:

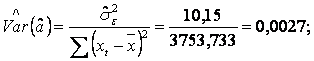
![]()
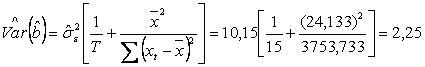
![]()
- calculul intervalelor de incredere pentru estimatori:
Variabilele aleatoare 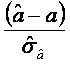 si
si  urmeaza fiecare o repartitie Student cu (T-2) grade de libertate. Alegand un nivel de semnificatie
α=0,05, putem extrage din tabelele repartitiei (astfel de tabele se gasesc
in majoritatea cartilor de econometrie, sau de statistica matematica) valoarea
ttab corespunzatoare numarului de grade de libertate si nivelului de
semnificatie ales. In cazul nostru, pentru T-2=13 grade de libertate si
α=5%, gasim ttab=2,16. Intervalele de incredere vor fi:
urmeaza fiecare o repartitie Student cu (T-2) grade de libertate. Alegand un nivel de semnificatie
α=0,05, putem extrage din tabelele repartitiei (astfel de tabele se gasesc
in majoritatea cartilor de econometrie, sau de statistica matematica) valoarea
ttab corespunzatoare numarului de grade de libertate si nivelului de
semnificatie ales. In cazul nostru, pentru T-2=13 grade de libertate si
α=5%, gasim ttab=2,16. Intervalele de incredere vor fi:
![]()
= [1,17 ; 1,39]
![]()
=[28,43 ; 34,91]
Prin urmare, putem afirma ca valorile parametrilor reali a si b se gasesc in aceste intervale cu o probabilitate de 95%.
Stabilim acum un interval de
incredere pentru estimatorul variantei erorilor. Am vazut ca variabila
aleatoare 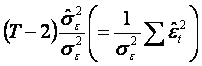 urmeaza o lege de repartitie hi-patrat cu (T-2) grade de
libertate. In tabelele legii hi-patrat vom gasi, pentru un nivel de
semnificatie α dat, doua valori: v1
avand probabilitatea (1-α/2) de a fi depasita, respectiv v2 avand probabilitatea
(α/2) de a fi depasita, astfel ca
urmeaza o lege de repartitie hi-patrat cu (T-2) grade de
libertate. In tabelele legii hi-patrat vom gasi, pentru un nivel de
semnificatie α dat, doua valori: v1
avand probabilitatea (1-α/2) de a fi depasita, respectiv v2 avand probabilitatea
(α/2) de a fi depasita, astfel ca
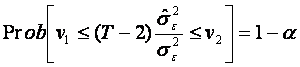
Se obtine astfel intervalul de incredere:
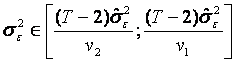
pentru =0,05 si 13 grade de libertate extragem din tabela v1=5,01 si v2=24,7 rezultand intervalul:
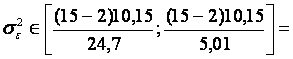
- testam daca parametrii a si b ai modelului sunt semnificativ diferiti de zero la pragul de semnificatie α=0,05.
Variabilele aleatoare ![]() si
si ![]() urmeaza legi de probabilitate Student cu (T-2)
grade de libertate. Aceste rapoarte se numesc si "raportul t" Student empiric
(tcalculat). Se accepta ipoteza H0: (a=0) daca tcalculat (luat
in modul) este mai mic decat ttabelat , altfel se
accepta ipoteza contrara H1:(a
urmeaza legi de probabilitate Student cu (T-2)
grade de libertate. Aceste rapoarte se numesc si "raportul t" Student empiric
(tcalculat). Se accepta ipoteza H0: (a=0) daca tcalculat (luat
in modul) este mai mic decat ttabelat , altfel se
accepta ipoteza contrara H1:(a![]() Acest
lucru se poate scrie:
Acest
lucru se poate scrie:
 . Este exact acelasi lucru cu a spune ca 0 sa apartina
intervalului de incredere determinat pentru a.
Cum
. Este exact acelasi lucru cu a spune ca 0 sa apartina
intervalului de incredere determinat pentru a.
Cum ![]() [1,17 ;
1,39], acceptam ipoteza H1:(a
[1,17 ;
1,39], acceptam ipoteza H1:(a![]() 0). La fel
stau lucrurile si pentru b. Prin
urmare, a si b sunt semnificativ diferiti de zero la pragul de semnificatie de
5%. Se spune ca variabila explicativa (exogena) X (varsta utilajului) este "contributiva".
0). La fel
stau lucrurile si pentru b. Prin
urmare, a si b sunt semnificativ diferiti de zero la pragul de semnificatie de
5%. Se spune ca variabila explicativa (exogena) X (varsta utilajului) este "contributiva".
- ne propunem acum sa
determinam o previziune a cheltuielilor de intretinere si reparatii pentru un utilaj de 4 ani (48 de luni).
Notam cu ![]() cheltuielile de intretinere si reparatii
pentru un utilaj cu "varsta"
cheltuielile de intretinere si reparatii
pentru un utilaj cu "varsta" ![]() . Avem ca
. Avem ca ![]()
Ce eroare corespunde unei astfel de previziuni? Stim ca:
![]() , este o variabila aleatoare distribuita
normal, cu media zero si varianta estimata a erorii de previziune:
, este o variabila aleatoare distribuita
normal, cu media zero si varianta estimata a erorii de previziune:
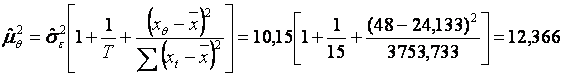
![]()
Deoarece variabila aleatoare
 este distribuita Student cu (T-2) grade de
libertate, putem determina un interval de incredere pentru valoarea
previzionata:
este distribuita Student cu (T-2) grade de
libertate, putem determina un interval de incredere pentru valoarea
previzionata:
 Cu o probabilitate de 95%,
valoarea adevarata a cheltuielilor de intretinere si reparatii pentru un utilaj
de 48 de luni se va afla in intervalul determinat.
Cu o probabilitate de 95%,
valoarea adevarata a cheltuielilor de intretinere si reparatii pentru un utilaj
de 48 de luni se va afla in intervalul determinat.
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 1910
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2026 . All rights reserved