| CATEGORII DOCUMENTE |
| Agricultura | Asigurari | Comert | Confectii | Contabilitate | Contracte | Economie |
| Transporturi | Turism | Zootehnie |
In anii '50 profesorul Harry Markovitz de la Universitatea din New York a gasit o abordare ingenioasa asupra investitiilor, care a devenit mai tarziu Teoria Moderna a Portofoliului (TMP). Spre deosebire de abordarea traditionala (bazata pe analiza tehnica si fundamentala) accentul cade pe analiza performantei intregului portofoliu (pe baza raportului randament/risc al componentelor sale). Pentru descoperirea sa revolutionara, Markowitz a primit Premiul Nobel pentru Economie in 1990. Teoria moderna a portofoliului este opusa ca filozofie de metoda traditionala de alegere a investitiilor. Este creatia economistilor, care incearca sa inteleaga piata ca intreg, spre deosebire de analistii financiari, care cercecteaza fiecare investitie in mod individual. Investitiile sunt modelate statistic, in termeni de profit asteptat si volatilitate. Volatilitatea este echivalenta cu riscul. Scopul este ca fiecare investitor sa-si identifice nivelul de risc acceptat si apoi sa gaseasca portofoliul cu cel mai mare randament pentru acel nivel de risc. Acest capitol acopera elementele esentiale ale Teoriei Moderne a Portofoliului, care incearca sa explice cum se masoara riscul si cum pot fi contracarate efectele sale.
1 Frontiera eficientei si diversificarea portofoliului
Intuitiv, beneficiile diversificarii sunt evidente. Imprastierea riscului pe mai multe industrii, pe mai multe tari sau pe mai multe companii, duce la reducerea semnificativa a riscului, mentinandu-se un profit ridicat. Analiza TMP a dovedit ca si un amestec aleator de titluri este mai putin riscant decat investirea intregii sume intr-o sigura companie.
Exista totusi un efect opus: daca ne limitam la portofolii cu un risc scazut, ne vom limita la investitii cu profitabilitate scazuta. Astfel, este indicata includerea in portofoliu si a unor investitii cu un grad de risc sporit (cu o rata profitului mare) si combinarea lor optima astfel incat o parte din fluctuatiile lor sa se anuleze. (se cauta un portofoliu cu o variatie standard mai mica decat a componentelor sale, luate separat). Luand in considerare datele pentru un numar mare de actiuni (un index, de exemplu S&P 500) se poate trasa un grafic cu variatia standard pe abscisa si rata profitului pe ordonata, a tuturor actiunilor componente si a portofoliilor care se pot obtine prin combinarea lor. Markowitz[1] a demonstrat ca se obtine o arie marginita superior de o curba crescatoare pe care a denumit-o frontiera eficientei (Grafic 1: Frontiera Eficientei). Este evident ca daca se alege o valoare fixa pentru σ, se doreste portofoliul care maximizeaza profitul (deci se alege un portofoliu de pe frontiera eficientei in locul unuia din interiorul ariei). In acelasi timp, frontiera eficientei este curbata, nu dreapta. Aceasta proprietate este esentiala in a demonstra ca diversificarea ajuta la imbunatatirea raportului profitabilitate/risc. Pentru a explica acest fenomen, se poate imagina o alocare egala intre doua investitii. Presupunand ca performantele anuale nu sunt perfect sincronizate, variatia standard a celor doua investitii luate impreuna va fi mai mica decat variatia standard a mediei lor cand sunt luate separat. In termeni statistici aceasta se datoreaza unui coeficient de corelatie mic (ρ). Cu cat ρ dintre cele doua investitii este mai mic, cu atat σ portofoliului este mai mic. In cel mai bun caz ρ poate fi -1 (investitii corelate perfect negativ).
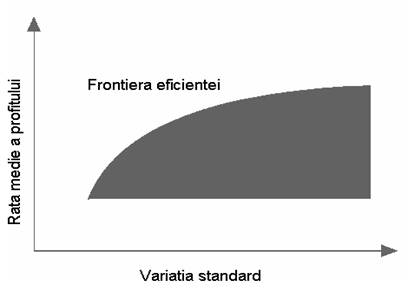
Grafic 1: Frontierea eficientei
2 Raportul Sharpe
In sectiunea precedenta s- a aratat care sunt portofoliile eficiente in raport cu riscul. Raportul Sharpe merge cu un pas inainte: ajuta la descoperirea proporitei in care trebuie luate investitiile, intr-un portofoliu care contine si active cu risc zero.
Raportul Sharpe este prin definitie:

unde:
. x este o investitie oarecare
![]() este rata medie
profitului anual al investitiei x
este rata medie
profitului anual al investitiei x
![]() este rata dobanzii la
depozite cu risc zero
este rata dobanzii la
depozite cu risc zero
![]() este variatia
standard a profitului investitiei x
este variatia
standard a profitului investitiei x
Raportul Sharpe este o masura a rentabilitatii raportata la risc. Pentru a explica modul in care este util in alegera portofoliului, se ia din nou in considerare frontiera eficientei la care se adauga si active cu risc zero.[2]

Grafic 3. Raportul Sharp
Sunt trei lucruri de notat in Grafic 3: Raportul Sharpe:
Daca se alege o combinatie intre investitia x si active fara risc, portofoliul ce va rezulta (Grafic 4: Portofoliul Optim), se va afla pe linia ce uneste activul fara risc cu investitia x (de data aceasta este o linie dreapta; punctul (0,Rf) avand variatia standard 0, anuleaza efectul de curbare la stanga).
Din moment ce se doreste un raport Sharpe cat mai mare, se va alege x astfel incat linia care trece prin el sa aiba panta cat mai mare.
Panta acestei linii este egala cu raportul sharpe al investitiei x.

Grafic 4: Portofoliul optim
Insumand cele de mai sus, o metoda de a alege portofoliul optim dintr-o multime de investitii date este: intai se alege portofoliul cu cel mai mare Raport Sharpe. Apoi se ia o combinatie liniara intre acesta si active cu grad de risc zero pana se ajunge la un σ corespunzator cu nivelul de risc tolerat. Va rezulta portofoliul cu cel ai mare randament posibil.[3]
Modelul de piata Sharp-Markowitz
Analistii bursieri si gestionarii de portofolii au constatat, din propria lor experienta, ca:
variatiile cursului oricarui titlu sunt mai mult sau mai putin legate de variatiile pietei in ansamblul sau; rare sunt titlurile care tind a se misca tot timpul invers decat piata in ansamblul sau ;
anumite titluri sunt mai volatile, mai sensibile decat altele la miscarile pietei. Volatilitatea unui titlu este descris prin sensibilitatea sa la miscarile pietei.
Aceasta relatie dintre rentabilitatea unui titlu si rentabilitatea pietei este formalizata prin intermediul modelului de piata. Cursul unui titlu poate varia sub influenta unor factori care afecteaza piata in ansamblul sau (factori macroeconomici, politici, legislativi, externi, etc.), caz in care vorbim despre riscul de piata. Dar cursul titlului poate varia si datorita unor factori strict legati de societate, caz in care vorbim despre riscul specific.
Modelul de piata a fost dezvoltat de Sharpe (1964) pornind de la
cercetarile lui Markowitz (1952) (1959). Este modelul[4]
cel mai cunoscut in descrierea rentabilitatii si riscului unei
investitii. Ideea modelului este ca variatia cursului unui
titlu, sau portofoliu de titluri, este determinata de piata, pe
de o parte si de alte cauze specifice, pe de alta. Relatia obtinuta,
considerata ca fiind liniara prin ipoteza (reprezentarea sa
grafica poarta denumirea de dreapta caracteristica)
poseda o panta ![]() si o
ordonata
si o
ordonata ![]()
Ecuatia dreptei care ajusteaza cel mai bine punctele date de
cuplurile ![]() va avea expresia :
va avea expresia :
![]()
unde :
![]() = rata de rentabilitate a actiunii
= rata de rentabilitate a actiunii ![]() , in perioada
, in perioada ![]()
![]() = rata de rentabilitate a pietei, in perioada
= rata de rentabilitate a pietei, in perioada ![]()
![]() = parametru propriu fiecarei actiuni, care
indica relatia care exista intre fluctuatiile actiunii
= parametru propriu fiecarei actiuni, care
indica relatia care exista intre fluctuatiile actiunii
![]() si
fluctuatiile pietei; se mai numeste coeficient de volatilitate
sau simplu beta ;
si
fluctuatiile pietei; se mai numeste coeficient de volatilitate
sau simplu beta ;
![]() = variabila specifica actiunii
= variabila specifica actiunii ![]() , care insumeaza
alti factori de influenta asupra titlului
, care insumeaza
alti factori de influenta asupra titlului ![]() , inafara de piata;
, inafara de piata;
![]() = parametru care arata locul de intersectie a
dreptei de regresie cu axa ordonatei, reprezentand rentabilitatea care ar putea
fi obtinuta de titlul
= parametru care arata locul de intersectie a
dreptei de regresie cu axa ordonatei, reprezentand rentabilitatea care ar putea
fi obtinuta de titlul ![]() , in conditiile in care rentabilitatea pietei este
0 .
, in conditiile in care rentabilitatea pietei este
0 .
![]() este egal cu
covarianta dintre rentabilitatea titlului
este egal cu
covarianta dintre rentabilitatea titlului ![]() si rentabilitatea
pietei, raportata la varianta ratei de rentabilitate a
pietei, dupa expresia:
si rentabilitatea
pietei, raportata la varianta ratei de rentabilitate a
pietei, dupa expresia:
![]()
Conform teoriei moderne a
portofoliilor, ![]() este elementul central
pentru ca el masoara riscul sistematic al acelui titlu sau
portofoliu. In functie de valoarea pe care o ia acesta, actiunile se
pot imparti in mai multe categorii :
este elementul central
pentru ca el masoara riscul sistematic al acelui titlu sau
portofoliu. In functie de valoarea pe care o ia acesta, actiunile se
pot imparti in mai multe categorii :
- actiuni cu volatilitate unitara: variaza in acelasi sens si in aceeasi proportie cu piata; achizitionarea unei astfel de actiuni presupune expunerea investitorului exact la riscul pietei ;
- actiuni cu volatilitate subunitara (nevolatile): variaza in acelasi sens dar intr-o proportie mai mica ca piata; expunerea la riscul pietei este mai mica, ele fiind actiunile "defensive";
- actiuni cu volatilitate supraunitara (volatile): variaza in acelasi sens dar intr-o proportie mai mare ca piata; sunt actiunile "ofensive" care amplifica variatia pietei si sunt atractive cand se anticipeaza o tendinta ascendenta a pietei .
Distinctia dintre risc sistematic si risc specific poate fi evidentiata pornind de la modelul de piata, prin aplicarea variantei, astfel:

adica : ![]()
Riscul sistematic este egal cu beta inmultit cu abaterea medie
patratica a pietei: ![]()
Riscul specific este egal cu abaterea medie patratica a
factorului rezidual : ![]() , aceasta fiind masura variabilitatii proprii
titlului.
, aceasta fiind masura variabilitatii proprii
titlului.
Riscul unui portofoliu depinde de trei factori:
riscul fiecarui titlu inclus in portofoliu;
covarianta dintre randamentele actiunilor din portofoliu;
numarul de titluri din portofoliu.[5]
Un portofoliu va fi cu atat mai riscant cu cat titlurile care-l contin
vor avea un ![]() mai mare. Gradul de
interdependenta a variatiilor de curs intre ele au o mare
importanta in reducerea
riscului portofoliului. In general,
doua actiuni nu vor varia de o maniera total independenta.
Covarianta lor este in general mai
mare de 0. In acest caz, reducerea riscului
nu este asa de mare ca si in cazul in care cele doua
actiuni vor varia independent. Componenta de piata a unui
portofoliu va varia de o maniera "sistematica" data de
incertitudinile pietei. Este imposibil de a elimina acest risc si
orice investitor si-l va asuma mai mult sau mai putin. Componenta
independenta a portofoliului data de factorii specifici
societatilor cotate poate fi eliminata usor prin diversificarea
portofoliului.
mai mare. Gradul de
interdependenta a variatiilor de curs intre ele au o mare
importanta in reducerea
riscului portofoliului. In general,
doua actiuni nu vor varia de o maniera total independenta.
Covarianta lor este in general mai
mare de 0. In acest caz, reducerea riscului
nu este asa de mare ca si in cazul in care cele doua
actiuni vor varia independent. Componenta de piata a unui
portofoliu va varia de o maniera "sistematica" data de
incertitudinile pietei. Este imposibil de a elimina acest risc si
orice investitor si-l va asuma mai mult sau mai putin. Componenta
independenta a portofoliului data de factorii specifici
societatilor cotate poate fi eliminata usor prin diversificarea
portofoliului.
Fie un portofoliu format din N
titluri, iar ![]() proportia in care s-a investit in titlul
proportia in care s-a investit in titlul ![]() , unde
, unde
![]() . Randamentul portofoliului va fi egal cu media
ponderata a randamentelor titlurilor care il compun, astfel:
. Randamentul portofoliului va fi egal cu media
ponderata a randamentelor titlurilor care il compun, astfel: ![]() . Daca in modelul
de piata in locul
randamentului titlului
. Daca in modelul
de piata in locul
randamentului titlului ![]() se va introduce
expresia de calcul a randamentului portofoliului, se va obtine expresia:
se va introduce
expresia de calcul a randamentului portofoliului, se va obtine expresia:
![]()
de unde se poate
observa ca ![]() si
si ![]() portofoliului sunt
egale cu mediile ponderate a lui
portofoliului sunt
egale cu mediile ponderate a lui ![]() si
si ![]() ale fiecarei
actiuni.
ale fiecarei
actiuni.
Efectul diversificarii se poate
observa, din relatia urmatoare, fara a pierde din
generalizare, presupunand ca toate titlurile individuale au acelasi
risc specific ![]() . Riscul unui portofoliu echiponderat, compus din N titluri,
va fi egal atunci cu:
. Riscul unui portofoliu echiponderat, compus din N titluri,
va fi egal atunci cu:
![]()
Cand ![]() , varianta portofoliului tinde spre
, varianta portofoliului tinde spre ![]() , iar riscul specific spre 0.
, iar riscul specific spre 0.
Relatia empirica care exista intre riscul unui portofoliu si numarul de titluri care il compun a fost studiata pentru prima data pe piata americana de Evans&Archer (1968), respectiv Wagner&Lau (1971) si de Solnik (1974) pentru principalele piete europene. Societatile din aceste portofolii au fost selectionate aleator. Rezultatele acestor studii arata ca un numar de 15 sau 20 de societati sunt suficiente pentru a face ca riscul specific sa tinda spre 0. Totodata este interesant de remarcat ca riscul de piata intr-un portofoliu foarte bine diversificat (peste 50 titluri) este situat intre 20% si 44% din riscul total al portofoliului.
Jaquillat&Solnik(1997) au identificat cinci posibilitati de aplicare practica a modelului de piata, astfel:
fixarea unui obiectiv de risc pentru portofolii;
utilizarea mai eficienta a previziunilor pietei;
orientarea analizei financiare;
masurarea performantelor portofoliilor gestionate;
completarea modelelor de evaluare a actiunilor.
Modelul de piata constituie un instrument puternic in intelegerea comportamentului pietelor financiare. El este in esenta foarte simplu, fiind fondat pe o metoda statistica elementara: regresia liniara simpla. Acest model constituie o prima formalizare cu caracter empiric a teoriei moderne a portofoliilor. Un al doilea model, cu un caracter accentuat normativ este Modelul de Echilibru a Activelor Financiare (MEAF). Conform acestuia pe o piata eficienta informational numai riscul de piata este remunerat. In aceste conditii estimarea acestui risc de piata si stabilitatea acestuia devine esentiala in teoria si practica moderna a portofoliilor.
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 3095
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2026 . All rights reserved