| CATEGORII DOCUMENTE |
| Astronomie | Biofizica | Biologie | Botanica | Carti | Chimie | Copii |
| Educatie civica | Fabule ghicitori | Fizica | Gramatica | Joc | Literatura romana | Logica |
| Matematica | Poezii | Psihologie psihiatrie | Sociologie |
SIRURI DE INTEGRALE
Cuprins
Notiuni teoretice
Aplicatii siruri de integrale
3) Calculul limitelor unor sume cu ajutorul integralelor
Bibliografie
Notiuni teoretice
Definitie:In analiza matematica, integrala unei functii este o generalizare a notiunilor de arie, masa, volum si suma. Procesul de determinare a unei integrale se numeste integrare.
Termenul 'integrala' se poate referi si la notiunea de primitiva o functie F a carei derivata este functia data f.
Exemple de integrale:
![]()
![]()
![]()

Definitie. Numim sir orice
functie ![]() ,
,
![]()
Notam ![]() . Sirul poate fi definit ca o infinitate de numere,distincte
sau nu,scrise unul dupa altul
. Sirul poate fi definit ca o infinitate de numere,distincte
sau nu,scrise unul dupa altul
Exemple de siruri:
2) 1, -1, 2, -2, ., n, -n, .
Aplicatii siruri de integrale
1) Fie ![]() .
.
a)
Sa se arate ca ![]() este monoton.
este monoton.
b)
Sa se gaseasca o relatie de recurenta intre ![]() si
si ![]()
c)
Sa se calculeze ![]()
Rezolvare:
![]()
![]() deoarece daca
deoarece daca ![]() .Cum
.Cum ![]() pentru
pentru ![]()
![]() si
si ![]() .Integrand prin parti se
obtine:
.Integrand prin parti se
obtine:
![]()
Se scrie relatia de recurenta: ![]() si se trece la limita 0.
si se trece la limita 0.
2) Fie ![]()
a) Sa se calculeze : ![]() si sa se stabileasca o relatie de recurenta
pentru
si sa se stabileasca o relatie de recurenta
pentru ![]()
Rezolvare:
![]()
![]() ;
;
![]()
![]()
3) Sa se stabileasca o relatie de recurenta pentru urmatoarele integrale:
a)![]()
b) ![]()
c) ![]()
Rezolvare:
a)![]()
b)![]()
c) ![]()
4) Fie sirul: ![]()
a) Sa se arate ca sirul ![]() este monoton si marginit.
este monoton si marginit.
b) Sa se gaseasca o relatie de recurenta intre ![]() si sa se calculeze
si sa se calculeze ![]()
Rezolvare:
a) Cum ![]() si deci
si deci ![]() ,iar de aici prin
integrarea
,iar de aici prin
integrarea ![]() .Deci
.Deci ![]() este marginit.De asemenea
este marginit.De asemenea![]() adica sirul
adica sirul ![]() este monoton descrescator.Conform teoriei lui
Weierstrass sirul
este monoton descrescator.Conform teoriei lui
Weierstrass sirul ![]() este convergent.
este convergent.
b) Integrand prin parti ![]() sau
sau ![]() .Trecand aici la limita
.Trecand aici la limita ![]()
5) Fie ![]() N
N
1. Sa se calculeze ![]()
2. Se cere ![]()
Rezolvare
1. ![]()
2. ![]() N
N
![]() N. Sirul
N. Sirul ![]() fiind descrescator si marginit inferior rezultand sir
convergent.
fiind descrescator si marginit inferior rezultand sir
convergent.
Din ![]() se deduce prin trecerea la limita
se deduce prin trecerea la limita ![]() .
.
Altfel, din ![]() se obtine
se obtine![]() .
.
6) Se considera ![]() N
N![]() .
.
a) Sa se calculeze ![]() ;
;
b) Sa se arate ca sirul
![]() este
monoton si marginit.
este
monoton si marginit.
Rezolvare:
a) ![]()
![]()
b) ![]() implica
implica ![]() pentru
pentru ![]() .
.
De aici ![]() si
si ![]() N
N![]() .
.
De asemenea ![]() pentru ca
pentru ca ![]() daca
daca
![]() si deci
si deci ![]()
![]() .
.
7) Se noteaza ![]() N.
N.
1. Sa se calculeze ![]() ;
;
2. Sa se arate ca ![]() .
.
Rezolvare:
1. ![]()
![]() ;
;
2. Se pune ![]() ,
deci
,
deci ![]() .
Avem
.
Avem ![]() .
De aici rezulta
.
De aici rezulta ![]() .
.
8) Fie sirul de functii ![]() R
R
![]() N si
N si
 .
.
Sa se calceleze ![]() .
.
Rezolvare
Avem ![]() ,
iar de aici prin integrare se obtine
,
iar de aici prin integrare se obtine ![]() .
.
Deci ![]() .
.
9) Fie ![]() R
R![]() R
R
![]() N
N![]() .
.
a) Pentru ![]() sa se calculeze
sa se calculeze ![]() ;
;
b) Fie ![]() R. Sa se stabileasca o relatie de
recurenta pentru
R. Sa se stabileasca o relatie de
recurenta pentru ![]() ;
;
c) Sa se arate ca ![]()
Rezolvare:
Avem ![]() .
.
Se spune ![]() ,
unde
,
unde ![]() .
.
Din ![]() se deduc relatiile de recurenta :
se deduc relatiile de recurenta : ![]() .
.
De aici ![]() ;
;
b) Integrand prin parti avem
: ![]() ;
;
c) Avem : ![]()
De aici rezulta ![]()
Dar ![]()
Deci ![]()
10) Fie sirul ![]() ,
, ![]()
![]()
![]()
a) Sa se arate ca ![]() ,
daca
,
daca ![]()
b) Sa se arate ca sirul ![]() este convergent
este convergent
c) Sa se calculeze ![]() .
.
Rezolvare :
a) Fie ![]() . Cum
. Cum ![]() daca
daca ![]() ,
atunci se deduce ca
,
atunci se deduce ca ![]() este descrescatoare pe
este descrescatoare pe ![]() . Deci din
. Deci din ![]() rezulta ca
rezulta ca ![]() .
.
b) Avem ![]() , daca
, daca ![]() si deci
si deci ![]() ,
care prin integrare da
,
care prin integrare da ![]()
![]() ; pe de alta parte
; pe de alta parte![]() , adica
, adica![]() este descrescator
.
este descrescator
.
c) Din punctul a) rezulta ca ![]()
11) Sa se arate ca ![]()
![]() .
.
Rezolvare:
Se integreaza prin parti si se obtine :

12) Se considera ![]() ,
, ![]() .
.
1) Sa se calculeze ![]()
2) Sa se calculeze ![]()
Rezolvare:
1) ![]()
2) 2, pentru ca ![]()
Calculul limitelor unor sume cu ajutorul integralelor

Unde: ![]()


![]()
![]()





![]()
![]()




![]()

![]()

![]()
![]()

![]()



![]()
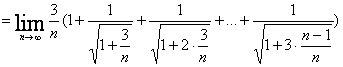

![]()
![]()
![]()







![]()
![]()


23). 
![]()
=![]()

![]() ,
,
![]()
![]()
25). 


![]()
![]()

![]()

![]()


![]()
![]()

=![]()
32) ![]() ,
, ![]() >0
>0
=![]() =
=![]() =
=![]()
![]() R ,
R , ![]()
![]()

33) 
![]()
![]() =
=
= =
=
=
 .
.
34) ![]()
![]() R ,
R , ![]()
![]() )
)
![]()
35) ![]()
![]() R ,
R , ![]()
![]() ; ...
; ...![]()
36) ![]() =
=![]()
=
![]() R ,
R , ![]()
![]()
![]() =
=![]()
37) ![]()


38) ![]()

39) 
=
40) 

41) 
![]()



|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 8487
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2026 . All rights reserved