| CATEGORII DOCUMENTE |
| Astronomie | Biofizica | Biologie | Botanica | Carti | Chimie | Copii |
| Educatie civica | Fabule ghicitori | Fizica | Gramatica | Joc | Literatura romana | Logica |
| Matematica | Poezii | Psihologie psihiatrie | Sociologie |
Problema de transport
Metoda transporturilor poartǎ aceastǎ denumire deoarece se foloseste pentru rezolvarea problemelor de programare liniarǎ ce au de a face cu deplasǎri de sarcini in retele de transport.
Prin extensie, metoda transporturilor se aplicǎ, in problemele de transbordǎri si asignare.
Aceasta problema apare frecvent in planificarea distribuirii bunurilor si a serviciilor de la cateva unitati de aprovizionare la anumite adrese.
De obicei cantitatea de bunuri aflate la fiecare unitate de aprovizionare (origine, furnizor, centru de productie, fabrici, oferta) este fixa sau limitata;
La fiecare unitate adresanta (sau destinatie, beneficiar, centru de distributie, cerere) se afla o cantitate de bunuri specificata prin comanda sau cerere.
Din cauza varietatii mari de rute de transport si a diferitelor costuri pentru aceste rute, obiectivul este de a stabili cate unitati de marfa pot fi transportate de la fiecare origine la fiecare destinatie in asa fel incat toate cererile sa fie satisfacute, iar costurile de transport sa fie micsorate.
Sa ilustram problema transportului
printr-un exemplu, sa zicem, al companiei Tofan Group care are de
transportat un produs de la 3 fabrici la 4 destinatii. Compania opereaza in Bucuresti,
Floresti si Brasov. Capacitatile de productie ale
acestor fabrici (cantitatile disponibile la furnizor ![]() in perioada urmatoare de 3 luni pentru un anume tip
de anvelope sunt:
in perioada urmatoare de 3 luni pentru un anume tip
de anvelope sunt:
1. Bucuresti 5000 unitati
2. Floresti 6000 unitati
3. Brasov 2500 unitati
Sa presupunem ca firma distribuie
anvelope prin 4 centre de distribuire regionale, localizate in Braila,
Cluj, Arad si Suceava, iar prognoza pe urmatoarele 3 luni de cerere
este (cantitati necesare la beneficiar![]()
1. Braila 6000 unitati
2. Cluj 4000 unitati
3. Arad 2000 unitati
4. Suceava 1500 unitati
Conducerea firmei ar dori sa stabileasca cat din productia sa trebuie transportata de la fiecare fabrica pana la fiecare destinatie de distribuire. Putem construi un grafic alcatuit din 2 grupuri de cercuri, numite noduri (fabrici si centre de distribuire) intre care se realizeaza 12 rute de distribuire, numite arce; graficul astfel obtinut se numeste retea. Se observa ca problema transportului poate fi reprezentata grafic sub forma unei retele, iar din acest motiv putem vorbi de problema fluxului in retea.
Observatie:Costurile de productie sunt identice la cele 3 fabrici, deci singurele costuri variabile implicate sunt cele de transport.
Astfel, problema devine una de determinare a
rutelor de transport care pot fi folosite si a cantitatii de
marfuri ce urmeaza a fi transportata pe fiecare ruta, in
asa fel incat toate cererile de distribuire sa fie onorate la un cost
minim de transport. Costul pentru fiecare unitate transportata pe
fiecare ruta este (matricea costurilor unitare de transport ![]()
|
Origine (Furnizori Fi) |
Destinatie( Beneficiari Bj) |
|||
|
Braila B1 |
Cluj B2 |
Arad B3 |
Suceava B4 |
|
|
Bucuresti F1 |
3 |
2 |
7 |
6 |
|
Floresti F2 |
7 |
5 |
2 |
3 |
|
Brasov F3 |
2 |
5 |
4 |
5 |
Pentru rezolvarea acestei probleme se poate folosi un model de programare liniara.
Vom folosi variabilele de decizie duble:
xij - numarul de unitati transportate de la origina i la destinatia j.
![]() matricea cantitatilor
transportate, planul de transport ce trebuie determinat si optimizat
matricea cantitatilor
transportate, planul de transport ce trebuie determinat si optimizat
cu notatiile:
i = indexul originii, i = 1,2,3
j = indexul destinatiei, j = 1,2,3,4
cij = costul per unitatea de transport de la originea i la destinatia j
ai = oferta sau capacitatea (disponibilul) exprimata in unitati la originea i
bj = cererea (necesarul) in unitati la destinatia j
De vreme ce obiectivul problemei transportului este de a minimaliza costurile de transport, putem folosi datele referitoare la cost din tabelul de mai sus pentru a elabora urmatoarele expresii ale costului:
Costuri de transport pentru unitati transportate
din Bucuresti = 3x11+2x12+7x13+6x14
din Floresti = 7x21+5x22+2x23+3x24
din Brasov = 2x31+5x32+4x33+5x34
Suma acestor expresii va furniza functia obiectiv care arata costurile totale de transport pentru firma Tofan Group.
Restrictiile problemei de programare liniara
- Cu 3 origini (sau fabrici) problema firmei Tofan Group va avea 3 formulari ale ofertei:
x11+x12+x13+x14 ≤ 5000 (oferta Bucuresti)
x21+x22+x23+x24 ≤ 6000 (oferta Floresti)
2x31+5x32+4x33+5x34 ≤ 2500 (oferta Brasov)
- Cu cele 4 centre de distribuire ca destinatii vom avea nevoie de urmatoarele 4 formule ale cererii:
x11+ x21+ x31 = 6000 (cerere Braila)
x12+ x22+ x32 = 4000 (cerere Cluj)
x13+ x23+ x33 = 2000 (cerere Arad)
x14+ x24+ x34 = 1500 (cerere Suceava)
Din combinarea functiei obiective cu formulele restranse intr-un singur model, reiese urmatoarea formulare de programare liniara cu 12 variabile si 7 restrictii in sistem:
(min) 3x11+2x12+7x13+6x14+7x21+5x22+2x23+3x24+2x31+5x32+4x33+5x34
|
x11 |
|
x12 |
|
x13 |
|
x14 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
≤ 5000 |
|
|
|
|
|
|
|
|
|
x21 |
|
x22 |
|
x23 |
|
x24 |
|
|
|
|
|
|
|
≤ 6000 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x31 |
|
x32 |
|
x33 |
|
x34 |
≤ 2500 |
|
x11 |
|
|
|
|
|
|
|
x21 |
|
|
|
|
|
|
x31 |
|
|
|
|
|
|
= 6000 |
|
|
|
x12 |
|
|
|
|
|
|
|
x22 |
|
|
|
|
|
|
x32 |
|
|
|
|
= 4000 |
|
|
|
|
|
x13 |
|
|
|
|
|
|
|
x23 |
|
|
|
|
|
|
x33 |
|
|
= 2000 |
|
|
|
|
|
|
|
x14 |
|
|
|
|
|
|
|
x24 |
|
|
|
|
|
|
x34 |
= 1500 |
Solutia data de computer pentru aceasta problema de programare liniara la care s-a redus problema de transport a firmei Tofan Group arata un cost minim de 39.500 unitati monetare. Valorile variabilelor arata cantitatile optime de marfa care se vor transporta pe fiecare ruta (x11=3500, x12=1500, x22=2500, x23=2000, x24=1500, x31=2500). Alte valori ale variabilelor de decizie arata cantitatile de marfa ramase de transportat si rutele.
Variatiile problemei de baza de transport pot include una sau mai multe din situatiile urmatoare:
Cu anumite modificari la modelul de programare liniara, aceste situatii pot fi luate in considerare atunci cand vrem sa obtinem solutia optima de transport.
Una din situatiile care apar frecvent este cea in care oferta totala nu este egala cu cererea totala (total disponibil difera de total necesar):
![]()
Diferenta dintre total disponibil si total necesar este absorbita de un beneficiar fictiv introdus in problema doar pentru a o echilibra si astfel a-i putea aplica algoritmul, costurile de transport asociate pe rutele care-l implica pe acest beneficiar fiind considerate nule.
![]()
modelul de programare liniara nu va avea o solutie practica deoarece conditiile cererii nu pot fi indeplinite; in acest caz este necesara o modificare in modelul de programare liniara pentru a ajunge la solutia dorita; mai precis, se foloseste o origine marioneta (furnizor fictiv) care sa absoarba diferenta pana la totalul cererii; se acorda un cost 0 pe unitatea transportata pe orice ruta pornind de la aceasta fabrica marioneta.
Intr-o solutie optima, destinatiile care arata transporturi primite de la furnizorul fictiv, vor fi destinatiile cu o cerere nesatisfacuta.
Observatii:
i) In unele modele poate fi mai convenabil sa luam in considerare mai degraba profitul sau beneficiile per unitate transportata decat costul per unitate. Folosind drept coeficienti profitul sau beneficiul in functia obiectiva vom rezolva un program liniar mai degraba maximizat decat minimizat.
ii) Formula problemei de transport poate fi mai departe modificata pentru a lua in calcul capacitatile de transport ale uneia sau ale mai multor rute. De exemplu, sa presupunem ca ruta Brasov Braila (originea 3 spre destinatia 1) are capacitatea de 1000 unitati din cauza spatiului limitat disponibil modului normal de transport. Aceasta capacitate limitata de transport a rutei poate fi luata in calcul prin adaugarea unei formule prescurtate care specifica o limita superioara pentru variabila de decizie corespunzatoare. Cu x31 aratand cantitatea de marfuri transportata din Brasov la Braila, formula prescurtata a capacitatii rutei va fi: x31 ≤ 1000
La fel cerintele minime ale rutei pot fi garantate; de exemplu: x22 ≥ 2000 va garanta ca o comanda emisa anterior pentru o livrare de la Floresti la Cluj de 2000 de unitati va fi mentinuta in solutia optima.
iii) Unele rute pot fi inacceptabile. Putem face fata acestei situatii acordand un cost arbitrar ridicat per unitate pentru oricare din rutele inacceptabile. Solutia costului minim de transport va evita ruta inacceptabila din cauza acestui cost.
Un mod alternativ de a lucra cu rute inacceptabile este pur si simplu indepartarea variabilei de decizie corespunzatoare din formularea programarii liniare; de exemplu, daca ruta Bucuresti Arad ar fi declarata inacceptabila, x13 ar putea fi scos din formula programarii liniare. Rezolvand modelul cu 11 variabile si 7 formule prescurtate am putea obtine solutia optima, garantand ca ruta Bucuresti Arad nu a fost folosita.
iv) - cij ), situatiile cij=- si cij=+ sunt rezervate pentru anumite probleme speciale: costul negativ are semnificatia de beneficiu pe unitatea de produs livrata.
Formularea economica a problemei de transport
Un produs se transporta de la m centre
furnizoare ![]() la n centre de
consum (beneficiari)
la n centre de
consum (beneficiari)![]()
Se cunosc:
matricea costurilor unitare de transport;
![]()
cantitatile disponibile la fiecare furnizor;
![]()
cantitatile necesare la fiecare beneficiar.
![]()
Se cere a se determina planul optim de transport, matricea cantitatilor transportate:
![]()
astfel incat costurile totale de transport sa fie minime.
Observatii:
Formularea matematicǎ a problemei de transport
![]()
![]() functia obiectiv (1)
functia obiectiv (1)
![]()
![]() restrictiile legate de surse (2)
restrictiile legate de surse (2)
![]() restrictiile legate de destinatii (3)
restrictiile legate de destinatii (3)
![]() ,
, ![]()
![]()
![]() conditiile de
conditiile de
nenegativitate ale variabilelor decizionale
(nu pot fi admise transporturi negative).
Conditia de echilibru: ![]()
T este cantitatea totala de marfa care se gaseste in depozite si care este ceruta de centrele de consum;
(2) reprezinta totalul cantitatilor transportate de de furnizorul Fi catre toti beneficiarii;
(3) reprezinta totalul cantitatilor transportate catre beneficiarul Bj plecand de la toti furnizorii;
numarul variabilelor este egal cu mn, iar al restrictiilor cu m+n;
matricea tehnologica are numai componente egale cu 0 sau 1;
restrictiile sunt egalitati;
Fiind deci o P.P.L., P.T. beneficiaza de algoritmul simplex pentru rezolvare. Una din metode este sa se treaca la forma duala a problemei si apoi sa se aplice algoritmul simplex. Totusi, forma ei speciala a permis introducerea altor metode de calcul, pornind cu determinarea solutiei initiale si sfarsind cu metoda de rezolvare. Pe acestea le vom prezenta in cele ce urmeaza.
Propozitie:
Orice problema de transport are o solutie admisibila.
Demonstratie:
Daca luam solutia ![]() atunci aceasta are in mod evident
componente pozitive si verifica sistemul de restrictii:
atunci aceasta are in mod evident
componente pozitive si verifica sistemul de restrictii:
![]()
![]()
Din aceasta propozitie rezulta ca orice problema de transport admite si o solutie optima.
Propozitie:
Rangul matricei A a restrictiilor unei probleme de transport echilibrate este egal cu m+n-1.
Demonstratie:
Matricea restrictiilor P.T. are forma:
|
|
|
1 |
1 |
|
1 |
0 |
0 |
|
0 |
|
0 |
0 |
|
0 |
|
|
|
|
|
0 |
0 |
|
0 |
1 |
1 |
|
1 |
|
0 |
0 |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m linii |
|
A= |
|
0 |
0 |
|
0 |
0 |
0 |
|
0 |
|
1 |
1 |
|
1 |
|
|
|
|
|
1 |
0 |
|
0 |
1 |
0 |
|
0 |
|
1 |
0 |
|
0 |
|
|
|
|
|
0 |
1 |
|
0 |
0 |
1 |
|
0 |
|
0 |
1 |
|
0 |
|
n linii |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
0 |
|
1 |
0 |
0 |
|
1 |
|
0 |
0 |
|
1 |
|
|
Adunand primele m restrictii se obtine:
![]()
![]() .
.
Se obtine in membrul stang suma tuturor variabilelor PT, iar in membrul drept suma T, adica restrictiile nu sunt independente. In loc de rangul m+n, A are rangul m+n-1.
Corolar:
O solutie de baza a PT are un numar de componente nenule egal cel mult cu m+n-1.
Ne intereseaza solutia de baza deoarece, solutia optima a problemei se afla printre solutiile realizabile de baza.
Determinarea unei solutii initiale de baza pentru P.T.
Exista mai multe metode speciale concepute in acest scop:
Vom ilustra aceste metode pe un exemplu.
Exemplu:
Un produs trebuie transportat de la 3 depozite D1, D2, D3 catre 4 centre de consum C1, C2, C3, C4. Costurile de transport, necesarul centrelor de consum si disponibilul depozitelor sunt date in tabelul de mai jos.
Sa se stabileasca ce cantitati trebuie transportate de la fiecare depozit la fiecare centru de consum, astfel incat costul total al transportului sa fie minim.
|
Depozite |
Centre de consum C1C2C3C4 |
|
Disponibil (t) |
|
D1 D2 D3 |
100 20 11 127 9 20 01416 18 |
|
15 25 5 |
|
Necesar (t) |
51515 10 |
45 |
45 |
Problema este echilibrata, variabilele de decizie sunt in numar de 12, deoarece aici numarul depozitelor este m=3, iar numarul centrelor de consum este n=4.
Aranjam variabilele in tabel, in fiecare casuta aparand si variabila respectiva xij si costul unitar de transport, asa cum este el dat in tabelul precedent (cele doua matrice C si X suprapuse in acelasi tabel)
|
10 |
0 |
20 |
11 |
|
x11 |
x12 |
x13 |
x14 |
|
12 |
7 |
9 |
20 |
|
x21 |
x22 |
x23 |
x24 |
|
0 |
14 |
16 |
18 |
|
x31 |
x32 |
x33 |
x34 |
Modelul primal este:
![]()
![]() [min]
[min]![]()
|
|
|
![]()
O solutie initiala de baza are exact m+n-1=3+4-1=6 componente nenule,daca este solutie nedegenerata de baza si un numar mai mic de 6 componente nenule daca este solutie degenerata de baza.
Metoda costului minim din tabel
Se alege minimul costurilor din tabel, in cazul exemplului nostru 0=c12
sau 0=c31 si se trimite pe ruta ![]() sau
sau ![]() cantitatea maxima posibil de
transportat, tinand seama de disponibil si de necesar. Prin urmare,
vom trimite:
cantitatea maxima posibil de
transportat, tinand seama de disponibil si de necesar. Prin urmare,
vom trimite:
x12=min=min=15t
pe ruta ![]() si in felul acesta, atat
disponibilul depozitului F1 cat si necesarul centrului B2
s-au epuizat. Rezulta ca x11=x13=x14=0
si ca x22=x32=0.
si in felul acesta, atat
disponibilul depozitului F1 cat si necesarul centrului B2
s-au epuizat. Rezulta ca x11=x13=x14=0
si ca x22=x32=0.
Apoi:
x31=min=min=5t,
deci x32=x33=x34=0 si x11=x21=0.
Acum mai raman de stabilit celelalte cantitati x23, x24. Alegem costul minim si constatam ca cel mai mic cost este 9=c23, deci x23=min=15, prin urmare x33=0 si urmeaza costul 20=c24, deci x24=min=10
Solutia initiala X0, determinata prin metoda minimului din tabel, este urmatoarea:
X0:
|
|
15 |
|
|
|
|
|
15 |
10 |
|
5 |
|
|
|
Ea are numai 4 componente nenule in loc de 6 , deci este o solutie degenerata de baza.
Valoarea functiei de
eficienta este ![]() unitati monetare.
unitati monetare.
Metoda minimului pe linie
Se porneste cu calculul variabilelor de pe prima linie si nu se paraseste aceasta linie pana cand nu au fost stabilite toate variabilele. Se alege costul minim de pe prima linie:
0=c12![]() x12=min=15t. Rezulta x11=x13=x14=0.
Disponibilul primei linii a fost epuizat.
x12=min=15t. Rezulta x11=x13=x14=0.
Disponibilul primei linii a fost epuizat.
Se trece la a doua linie. Costul minim de pe a doua linie este 7=c22,
dar x22=0 deoarece centrul B2 si-a satisfacut
necesarul prin alegerea x12=15. Urmeaza in ordinea marimii
c23=9![]() x23=min=15t.
x23=min=15t.
Raman de repartizat inca 10 t ale depozitului F2.
Costul urmator este c21=12![]() x21=min=5t, etc.
x21=min=5t, etc.
Prin metoda minimului pe linie s-a aflat solutia:
|
|
15 |
|
|
|
5 |
|
15 |
5 |
|
|
|
|
5 |
X1=
![]() unitati
monetare. Solutia este degenerata.
unitati
monetare. Solutia este degenerata.
Solutia initiala aflata prin metoda minimului pe coloana se afla la fel ca aceea determinata prin metoda minimului pe linie, numai ca repartizarea se face pe centre de consum, deci pe coloane.
Metoda coltului de Nord-Vest pentru alegerea unei solutii initiale de baza
Aceasta metoda nu are in vedere criteriul economic al costurilor, ci numai amplasarea formala a marfii dupa pozitia componentei in tabel. Au prioritate componentele aflate in coltul de N-V al tabelului.
Astfel,x11 este prima componenta din coltul de N-V al tabelului. O alegem automat si o luam egala cu 5t, deoarece:
x11= min=min=5t.
Taiem cu o linie coloana 1, deoarece necesarul lui B1 a fost satisfacut si catre el nu se vor mai face transporturi.
Urmatorul colt de N-V al tabelului a ramas dupa ce am eliminat coloana intai si este al variabilei x12, a carei marime urmeaza sa o stabilim astfel:
x12=min=10.
Taiem linia intai, deoarece F1 nu mai are disponibil, iar necesarul centrului B2 ramane egal cu 5.
In tabelul ramas, coltul de N-V este al casutei (2.2) deci
x22=min=5t.
Se trece la coloana a doua si ramane x23 in coltul de N-V. Luam x23=min=15t, deci coloana a treia urmeaza sa fie anulata, iar disponibilul lui F2 ramane egal cu 5. Coltul de N-V al tabelului ramas este (2,4), deci
x24=min=5t
In sfarsit, a ramas numai x34=5t si solutia X2 obtinuta prin metoda coltului de N-V este:
X2=
|
5 |
10 |
|
|
|
|
5 |
15 |
5 |
|
|
|
|
5 |
![]() unitati
monetare. Aceasta solutie nu este degenerata.
unitati
monetare. Aceasta solutie nu este degenerata.
Observatie: Dintre cele trei solutii determinate, cea mai buna, desigur, este solutia X0, deoarece functia de eficienta are valoarea cea mai mica.
Metoda potentialelor pentru determinarea unei solutii optime a P.T.
Este o metoda de testare si de optimizare a solutiei unei P.T. si are la baza rezultatele P.L. (simplexul aplicat formei duale a P.T.)
Pas 1. Se determina o solutie initiala de baza
Pas 2. (criteriul de optim) Se testeaza solutia obtinuta cu ajutorul unei conditii de optim. Daca solutia se gaseste optima, STOP. Daca nu, se trece la pasul 3.
Pas 3. (criteriul de intrare in baza) Se determina o variabila dintre cele nebazice care sa intre in baza, sa devina nenula deci si pentru care solutia se imbunatateste.
Pas 4. (criteriul de iesire din baza) Se determina o variabila care paraseste baza, utilizand conditia de admisibilitate. Se obtine astfel o alta solutie de baza care trebuie din nou verificata daca este optima, deci se reia algoritmul de la pasul 2.
Rezultatul teoretic care sta la baza acestei metode de optimizarea unei solutii primal admisibile pentru problema de transport este:
Teorema Dantzig (conditia de optimalitate)
Fiecarei variabile bazice xij a
unei solutii de baza ii corespunde un cuplu de numere reale ui,
vj astfel incat ![]() . Daca pentru variabilele bazice notam
. Daca pentru variabilele bazice notam ![]() , atunci solutia optima se obtine
daca toate diferentele
, atunci solutia optima se obtine
daca toate diferentele ![]() sunt negative (
sunt negative (![]()
Demonstratie: Se aplica algoritmul simplex de optimizare a solutiei initiale de baza pentru forma duala a unei probleme de transport echilibrate.
Vom considera , pentru simplificarea scrierii, cazul m=2, n=3; rezultatele obtinute vor fi valabile si in cazul general. Modelul (PL) corespunzator va fi:
![]() (min) f=c11x11+c12x12+c13x13+c21x21+c22x22+c23x23
(min) f=c11x11+c12x12+c13x13+c21x21+c22x22+c23x23
![]() x11+x12+x13 = a1 (variabila duala:u1)
x11+x12+x13 = a1 (variabila duala:u1)
x21+x22+x23 = a2 (variabila duala:u2)
x11+x21=b1 (variabila duala:v1)
x12+x22=b2 (variabila duala:v2)
x13+x23=b3 (variabila duala:v3)
xij 0; i=1,2; j=1,3
Modelul dual corespunzator are aspectul:
![]() (max)g=a1u1+a2u2+b1v1+b2v2+b3v3
(max)g=a1u1+a2u2+b1v1+b2v2+b3v3
![]() u1+v1 c11
u1+v1 c11
u1+v2 c12
u2+v1 c21
u1+v3 c13
u2+v2 c22
u2+v3 c23 ui+vj cij; i=1,2; j=1,3
ui,vj IR
Se stie ca pentru orice solutie X a modelului primal, si pentru orice solutie Y a modelului dual, avem: g(y) f(x)
max = min
y x
In general, modelul dual al P.T. este:
![]()
![]()

Daca in g inlocuim ai,bj cu expresiile date de sistemul primal, obtinem:
![]()
In final, din relatia: g(y) f(x) se deduce:
![]()
![]()
aceasta relatie permite organizarea rezolvarii.
Daca se alege o solutie posibila oarecare a modelului, ea este solutia de baza (adica are sanse sa fie solutie optima) daca are numaul de componente Xij*>0 cel mult egal cu m+n-1.
pentru indicii i,j pentru care xij*>0, se rezolva sistemul
ui+vj=cij
Observatie:
acest sistem este intotdeauna compatibil
nedeterminat, m+n-1 ecuatii liniare cu m+n necunoscute, avand una din necunoscute secundare pentru care se alege o valoare arbitrara.
pentru indicii i,j care participa la scrierea
sistemului, termenii ramasi sunt nuli din cauza faptului ca Xij* = 0;
Aparent, expresia ui+vj=cij are aspectul cerut de conditia de optim (sub rezerva ca e nevoie ca, pentru i,j care nu participa la scrierea sistemului, sa avem: ui+vj cij)
- daca conditia ui+vj cij ![]()
![]() nu este indeplinita,
atunci nu este solutie optima si
vom constitui o alta solutie
imbunatatita.
nu este indeplinita,
atunci nu este solutie optima si
vom constitui o alta solutie
imbunatatita.
1. Fie problema de transport:
|
|
B1 |
B2 |
B3 |
disponibil |
|
F1 |
5 |
1 |
7 |
50 |
|
F2 |
4 |
3 |
2 |
120 |
|
F3 |
2 |
9 |
10 |
80 |
|
necesar |
75 |
90 |
85 |
total: 250 |
Se cere solutia de cost total minim.
Solutie:
Folosim metoda potentialelor pentru verificarea optimalitatii solutiei initiale x0:
|
|
50 |
|
|
35 |
|
85 |
|
40 |
40 |
|
Rezolvam sistemul ui+vj=cij pentru acei indici aflati
in celulele ocupate ale solutiei X0, adica pentru indicii bazici.
|
vj ui |
3 |
10 |
1 |
|
-9 |
-6 |
1 |
-8 |
|
1 |
4 |
11 |
2 |
|
-1 |
2 |
9 |
0 |
Sistemul e simplu nedeterminat (6 ecuatii,5 necunoscute), deci se
pleaca de la o valoare arbitrara pentru una din variabilele duale;
solutia particulara determinata pentru acest sistem se trece
intr-un tabel, adica in matricea ![]()
- apoi se testeaza ![]()
![]() :
:
|
-11 |
0 |
-15 |
|
-3 |
[8] |
0 |
|
-3 |
-7 |
-10 |
Cum exista ![]() , atunci solutia nu este optima si se trece la
imbunatatirea ei.
, atunci solutia nu este optima si se trece la
imbunatatirea ei.
intra o valoare arbitrara q pe pozitia (2,2) din matricea
diferenta, unde s-a gasit cea mai mare dintre valorile pozitive ce nu satisfac criteriul de optim.
determinam un ciclu poligonal cu laturi verticale si
orizontale, avand numai varfuri in casute (celule) ocupate in matricea solutiei X0 , varfuri pe care le numerotam alternativ cu +q q q q,, etc;
q se alege minimul valorilor aflate in celulele cu semnul -; q=min=35;
- rezulta modificarile in matricea solutiei x0, care arata variabila ce paraseste baza.
|
|
50 |
|
|
|||
|
35-q |
q |
85 |
|
|||
|
40+q |
40-q |
|
|
|||
|
X1= |
|
50 |
|
|||
|
|
- |
35 |
85 |
|||
|
|
75 |
5 |
|
|||
|
vj ui |
-7 |
0 |
-1 |
|
|
|
|
|
1 |
-6 |
1 |
0 |
|
-11 |
0 |
-7 |
|
3 |
-4 |
3 |
2 |
|
-8 |
0 |
-1 |
|
9 |
2 |
9 |
8 |
|
0 |
0 |
-8 |
|
11 |
|
7 |
|
8 |
|
|
|
|
|
2 |
Pentru solutia nou gasita x1 s-a reluat
algoritmul, rezolvandu-se iar sistemul cu noile variabile duale, s-a construit
dinnou matricea costurilor reduse, ![]() si s-a verificat conditia de optim, care stabileste ca
x1 este optima.
si s-a verificat conditia de optim, care stabileste ca
x1 este optima.
Sa comparam functiile obiectiv pentru cele doua solutii:
![]()
![]()
![]() , iar
, iar ![]()
Observatii:
-
daca Dij![]() 0 ( )i,j si ( ) (i0,j0) pentru care Diojo
=0, atunci modelul admite inca o solutie optima de baza, cu
xiojo 0;
0 ( )i,j si ( ) (i0,j0) pentru care Diojo
=0, atunci modelul admite inca o solutie optima de baza, cu
xiojo 0;
daca modelul admite solutiile optime de baza
x1,x2,.,xk, atunci x=l1x1+l2x2+.+lkxk, unde l1 l2 lk=1, lj 0, j=1,k, este tot o solutie optima (care nu e de baza).
2 .Fie problema de transport:
|
furnizori |
|
beneficiari |
|
||
|
|
B1 |
B2 |
B3 |
disponibil |
|
|
F1 |
8 |
4 |
2 |
65 |
|
|
F2 |
6 |
3 |
1 |
130 |
|
|
F3 |
10 |
7 |
5 |
45 |
|
|
Necesar |
80 |
75 |
85 |
total:240 |
|
a)Se cere solutia optima a problemei.
b)Se cere solutia optima pentru care avem:
x23=maxim
x31+2x23 80
Solutie:
Vom aplica metoda potentialelor: drept solutie initiala, folosim
|
|
v1=7 |
v2=3 |
v3=1 |
|
u1=1 |
8 |
4 |
2 |
|
u2=0 |
7 |
3 |
1 |
|
u3=3 |
10 |
6 |
4 |
|
35 |
30 |
|
|
|
45 |
85 |
|
45 |
|
|
X0=
|
35-q |
30+q |
|
|
q |
45-q |
85 |
|
45 |
|
|
|
|
65 |
0 |
|
35 |
10 |
85 |
|
45 |
|
|
X1 :
|
|
v1=5 |
v2=2 |
v3=0 |
|
u1=2 |
7 |
4 |
2 |
|
u2=1 |
6 |
3 |
1 |
|
u3=5 |
10 |
7 |
5 |
|
35 |
30 |
|
|
|
45 |
85 |
|
45 |
|
|
Deci solutia
X2 =
X2 se gaseste optima.
Cum tabelul diferentei D contine trei valori zero problema data mai are inca alte trei solutii optime de baza, notate X3,X4,X5.
|
|
65-q |
q |
|
35 |
10+q |
85-q |
|
45 |
|
|
|
|
|
65 |
|
35 |
75 |
20 |
|
45 |
|
|
![]() => X3=
=> X3=
|
|
65 |
|
|
35+q |
10 |
85-q |
|
45-q |
|
|
|
|
65 |
|
|
70 |
10 |
50 |
|
10 |
|
35 |
![]() => X4 =
=> X4 =
|
|
65 |
|
|
45 |
|
85 |
|
35 |
10 |
|
|
|
65 |
|
|
35+q |
10-q |
85 |
|
45-q |
q |
|
![]() => X5 =
=> X5 =
Solutia optima generala XG este data de:
XG= l1x2+l2x3+l3x4+l4x5
Unde: l1 l2 l3 l4=1
l1,2,3,4 0
Avem:XG=
|
65l2+65l3 |
65l4 |
65l1 |
|
35l1+35l2+80l3+45l4 |
10l1+75l2+10l3 |
85l1+20l2+40l3+85l4 |
|
35l4 |
45l1+45l2+45l3+10l4 |
|
b) Din XG, gasim: x23=
=85l1+20l3+85l4=20(13l1+4l3+13l4)+5(l1 l2 l3 l4
=20+5(13l1+4l3+13l4
x31+2x22=6l1+195l2+20l3+35l4=20(l1 l2 l3 l4)+5(9l1+35l2 l4)=20(9l1+35l2 l4
Problema devine:
(maxim)f=133l1+4l3+13l4
13l1+4l3+13l4 12
l1 l2 l3 l4=1
l1,2,3,4 0
aceasta problema se rezolva folosind algoritmul simplex.
TESTE DE AUTOEVALUARE
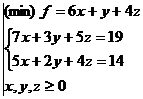 R: x=0,y=3,z=2; optim 11.
R: x=0,y=3,z=2; optim 11.1. Coordonatele unui vector intr-o baza. Modificarea coordonatelor unui vector la schimbarea bazei.
2. Demonstrati cu ajutorul algoritmului Simplex ca problema nu are solutii posibile:

3. Sa se aduca la expresia canonica
forma patratica: ![]() , utilizand metoda valorilor si vectorilor proprii.
Sa se determine si baza corespunzatoare.
, utilizand metoda valorilor si vectorilor proprii.
Sa se determine si baza corespunzatoare.
1. Subspatii liniare (Definitie, exemple, operatii cu subspatii).
2. Sa se costruiasca modelul matematic asociat problemei de mai jos si sa se determine solutia optima pentru problema de programare liniara rezultata, utilizand algoritmul simplex:
In cadrul unei livezi sunt destinate 8 ha de teren pentru a se cultiva doua feluri de plante A si B. Investitiile necesare pe hectar sunt respectiv de 2000 u.m. si 5000 u.m. iar castigul net pe ha este de 30000 u.m., respectiv 60000 u.m. Se investesc 25000 u.m. in cultura celor doua feluri de plante. Pe cate ha trebuie cultivate fiecare din aceste plante, pentru ca sa se obtina un beneficiu cat mai mare?
R: ![]() ; optim 330000.
; optim 330000.
3. Utilizand metoda Jacobi sa se aduca la o expresie canonica forma patratica:
1. Operatori liniari pe spatii vectoriale (Definitie, exemple, operatii; nucleul si imaginea unui operator liniar).
2. Sa se rezolve problema de programare liniara prin trecere la forma duala:
 R:
R: ![]() ; optim 12.
; optim 12.
3. Sa se studieze liniar
independenta vectorilor din ![]() :
:
![]() si sa se
descompuna vectorul
si sa se
descompuna vectorul ![]() in baza formata
de acestia.
in baza formata
de acestia.
1. Forme fundamentale ale PPL, solutii, clasificare (interpretare economica).
2. Sa se diagonalizeze matricea A=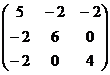 si sa se determine
si sa se determine ![]() . Sa se precizeze baza fata de care maricea A
admite forma diagonala.
. Sa se precizeze baza fata de care maricea A
admite forma diagonala.
3. Sa se determine costul minim de
transport daca se cunosc: matricea costurilor unitare de transport,
cantitatile disponibile la fiecare furnizor![]() si cele necesare fiecarui beneficiar
si cele necesare fiecarui beneficiar ![]() ca in tabloul:
ca in tabloul:
|
|
|
|
|
Disponibil |
|
|
1 |
2 |
8 |
37 |
|
|
1 |
11 |
1 |
45 |
|
|
14 |
7 |
3 |
18 |
|
Necesar |
26 |
63 |
11 |
|
R: 325
1. Algoritmul Simplex primal (enunt si interpretare economica).
2. O intreprindere comerciala dispune de
800 tone de fructe aflate in trei depozite ![]() , repartizate astfel: in
, repartizate astfel: in ![]() sunt 450 tone, in
sunt 450 tone, in ![]() sunt 150 iar 200 tone
in
sunt 150 iar 200 tone
in ![]() . Aceasta cantitate trebuie transportata la
doua fabrici
. Aceasta cantitate trebuie transportata la
doua fabrici ![]() astfel: la
astfel: la ![]() 550 tone, iar la
550 tone, iar la ![]() 250 tone. Matricea
costurilor unitare de transport este urmatoarea:
250 tone. Matricea
costurilor unitare de transport este urmatoarea: 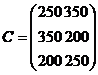 . Se cere planul optim de transport.
. Se cere planul optim de transport.
3. Sa se determine matricea operatorului
liniar 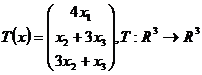 si sa se diagonalizeze, precizand baza
corespunzatoare.
si sa se diagonalizeze, precizand baza
corespunzatoare.
Nota asupra examinarii
Examinarea se face in scris, cu bilet individual ce contine o cerinta teoretica si doua aplicatii din tematica aferenta examenului respectiv.
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 555
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2026 . All rights reserved