| CATEGORII DOCUMENTE |
| Statistica |
Metode de analiza previzionala
economico - financiara
1. Metode cantitative de analiza previzionala
Gestiunea financiara a intreprinderii si mentinerea echilibrului financiar al acesteia au la baza anticiparea fluxurilor pozitive si negative, pe perioade scurte si medii, inainte de a imobiliza importante capitaluri.
Previziunea financiara are rolul ca, prin obiectivele activitatii viitoare, sa precizeze politica economica si financiara a firmei. Astfel se stabilesc proportiile in activitatea de exploatare, se concretizeaza strategia si politica financiara a intreprinderii, cu influente pozitive asupra desfasurarii procesului de productie si a fenomenelor economico-financiare.
Si in domeniul financiar, prognoza apare ca o activitate de evaluare probabilistica a evolutiei viitoare a unor fenomene.
Dintre metodele uzuale folosite in studiile de prognoza amintim metoda extrapolarii.
Metoda extrapolarii se bazeaza pe ipoteza ca evolutia unor conditii care au imprimat anumite tendinte in trecut, poate fi cunoscuta si transpusa si pentru o perioada viitoare. Aceasta este metoda cel mai des utilizata in prognoze cantitative si se bazeaza pe un ansamblu de functii de regresie si functii de trend. Astfel de functii au in vedere forma evolutiei fenomenelor, fie ea liniara, neliniara, uniforma, neuniforma.
Transpunerea practica a metodei extrapolarii se realizeaza pe baza:
- sporului mediu;
- ritmului mediu;
- metodei celor mai mici patrate.
Metode de prognoza bazate pe sporul mediu
Se aplica in cazul evolutiei uniforme, liniare a unui fenomen, pentru rezolvarea urmatoarelor probleme de prognoza:
- determinarea nivelului unui fenomen pentru un orizont de prognoza dat;
- determinarea orizontului prognozei in care un fenomen va atinge un nivel prestabilit;
- stabilirea orizontului prognozei necesar egalizarii unui indicator din doua firme sau zone diferite;
- egalizarea nivelului de dezvoltare a doua firme sau zone peste o perioada de timp prestabilita.
Orizontul prognozei este perioada de timp cuprinsa intre momentul prezent si un moment oarecare din viitor.
In ipoteza evolutiei dupa o progresie aritmetica, unor cresteri egale pentru variabila timp le corespund cresterii egale pentru variabila prognozata.
Functia de trend in conditiile metodei sporului mediu are forma:
![]() ,
,
![]() - nivelul prognozat al
indicatorului y;
- nivelul prognozat al
indicatorului y;
![]() - nivelul
indicatorului din perioada de baza, apropiat de media seriei;
- nivelul
indicatorului din perioada de baza, apropiat de media seriei;
n - diferenta dintre fiecare an si anul baza de calcul;
![]() - sporul mediu
- sporul mediu ![]() , unde:
, unde:
![]() - ultimul termen al
seriei;
- ultimul termen al
seriei;
![]() - primul termen al
seriei;
- primul termen al
seriei;
n - numarul termenilor seriei.
Daca si in perspectiva indicatorul y se va dezvolta tot in progresie aritmetica, cu aceeasi ratie, sporul mediu, valorile pe care le va atinge in anii viitori sunt:
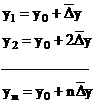
Metode de prognoza bazate pe ritmul mediu
In evolutia unor fenomene se intalneste si modelul unei progresii geometrice. Prognoza unor astfel de fenomene se realizeaza cu ajutorul unor metode bazate pe ritmul mediu de crestere.
Cunoscand
ca un indicator y a avut o dezvoltare trecuta cu un ritm mediu anual
de crestere ![]() , se doreste sa se stabileasca care va fi
nivelul indicatorului peste n ani, stiind ca in momentul
efectuarii prognozei nivelul indicatorului este y0.
, se doreste sa se stabileasca care va fi
nivelul indicatorului peste n ani, stiind ca in momentul
efectuarii prognozei nivelul indicatorului este y0.
Nivelul viitor al indicatorului va fi:
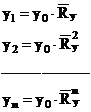
unde,
![]() - ritmul mediu anual
- ritmul mediu anual
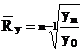 ,
,
iar
![]() - ultimul termen al
seriei;
- ultimul termen al
seriei;
![]() - primul termen al
seriei;
- primul termen al
seriei;
n - numarul termenilor seriei.
Metode de prognoza bazate pe metoda celor mai mici patrate
Metoda celor mai mici patrate consta in aproximarea valorilor reale ale seriei in asa fel incat functia ce se va obtine si care exprima tendinta fenomenului, sa se apropie in mare masura de datele reale ale acesteia.
Aceasta metoda se poate aplica pentru:
- functia liniara;
- parabola de gradul doi;
- hiperbola.
Functia liniara
Are forma: ![]() .
.
Parametrii a si b, in conditiile metodei celor mai mici patrate, se determina pe baza relatiilor
![]() , cu conditia ca
, cu conditia ca ![]() , unde:
, unde:
n - numarul termenilor seriei;
t - diferenta dintre fiecare an si anul situat in centrul sirului.
Determinarea indicatorului y pentru urmatorii n ani se face astfel:
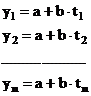
Parabola de gradul doi
Se utilizeaza cand fenomenul prognozat prezinta o tendinta crescatoare sau descrescatoare, cu un punct de maxim sau minim. Are forma:
![]() .
.
Aplicand metoda celor mai mici patrate obtinem sistemul de ecuatii normale:
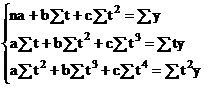
Facand
simplificarea ![]() = 0, sistemul devine:
= 0, sistemul devine:
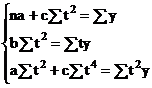
De aici se obtin parametrii a, b, c.
Nivelul indicatorului y pentru urmatorii n ani devine:

Hiperbola
Este
descrisa de functia: ![]()
Parametrii a si b, in conditiile metodei celor mai mici patrate se determina rezolvand sistemul de ecuatii normale:
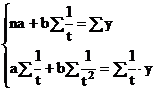
Daca ![]() = 0, atunci sistemul devine:
= 0, atunci sistemul devine:
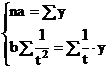
De aici se determina parametrii a si b, astfel:
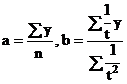
Nivelul indicatorului y pentru perioada viitoare:
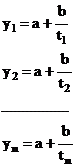
Toate aceste metode bazate pe trend au comun faptul ca timpul este o variabila de prognoza.
2. Proiectarea fluxurilor financiar - monetare la nivelul firmei
In functie de tendinta evidentiata se aplica una din metodele de prognoza prezentate (cea care se potriveste tendintei), pentru:
proiectarea fluxurilor de incasari si plati;
proiectarea fluxurilor de lichiditati.
Exemple - proiectia fluxurilor de incasari si plati.
Presupunem urmatoarea evolutie a incasarilor unei firme (mii RON).
|
Luna |
Incasari
|
|
Seria ajustata
|
|
|
|
||||
|
|
||||
|
|
||||
|
|
||||
|
|
||||
|
|
||||
|
|
||||
|
|
||||
|
|
||||
|
|
||||
|
|
||||
|
|
||||
|
Total | ||||
|
|
proiectii |
|||
|
|
||||
|
|
||||
|
|
||||
|
|
||||
|
|
||||
Sa se determine proiectia incasarilor pentru urmatoarele 6 luni, cu ajutorul metodei sporului mediu.
![]()
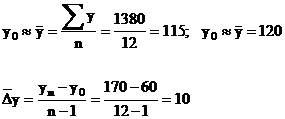
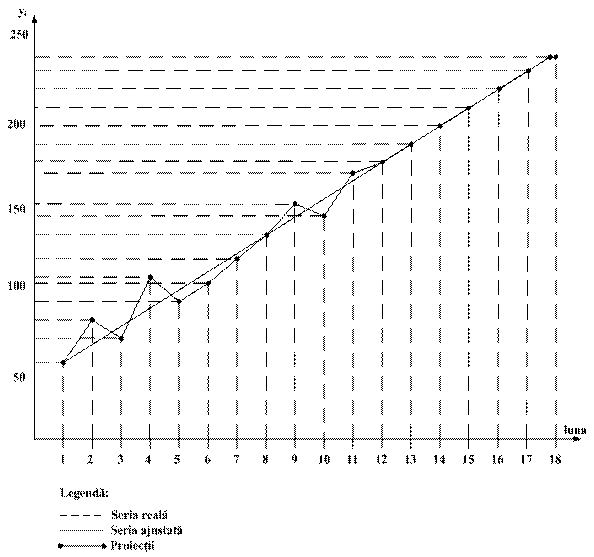
Presupunem urmatoarea evolutie a fluxului de plati a unei firme (mii RON).
|
Luna |
Plati
|
|
Seria ajustata
|
|
|
|
||||
|
|
||||
|
|
||||
|
|
||||
|
|
||||
|
|
||||
|
|
||||
|
|
||||
|
|
||||
|
|
||||
|
|
||||
|
|
||||
|
Total | ||||
|
|
proiectii |
|||
|
|
||||
|
|
||||
|
|
||||
|
|
||||
|
|
||||
Sa se stabileasca proiectia fluxului de plati cu ajutorul metodei ritmului mediu.
![]() ;
; ![]()
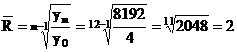 ;
; ![]()
Presupunem urmatoarea evolutie a incasarilor unei firme (mii RON).
|
Luna |
Incasari
|
|
|
|
Seria ajustata
|
|
|
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
|
Total | ||||||
|
|
proiectii |
|||||
|
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
|
|
||||||
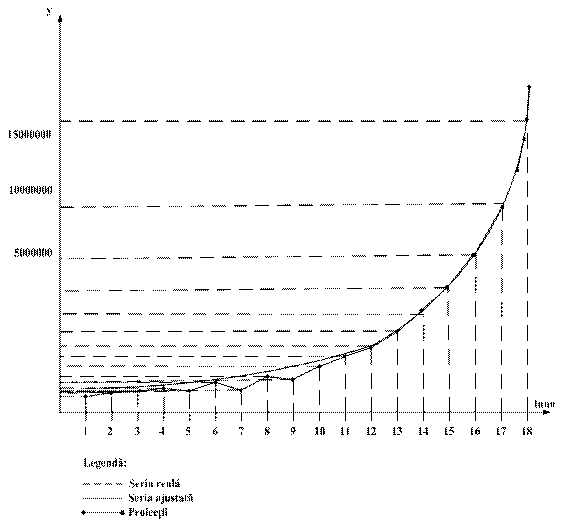
Sa se stabileasca proiectia incasarilor pentru urmatoarele 6 luni, cu ajutorul metodei celor mai mici patrate - dreapta.
![]() ;
; ![]() ;
; ![]()
Presupunem urmatoarea evolutie a fluxului de numerar (mii RON):
|
Luna |
Flux
numerar |
|
|
|
|
|
Seria ajustata
|
|
|
| ||||||||
|
Total | ||||||||
|
proiectii |
||||||||
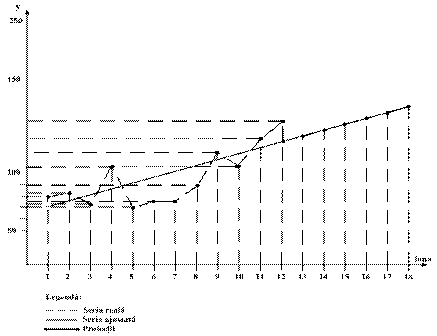
Sa se determine proiectia fluxului de numerar pentru urmatoarele 6 luni, prin metoda celor mai mici patrate - parabola.
![]()
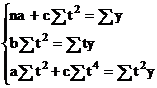
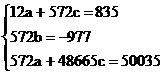
rezulta 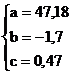

Presupunem urmatoarea evolutie a fluxului de numerar (mii RON) a unei firme:
|
Luna |
Flux numerar
|
|
|
|
|
|
Seria ajustata
|
||
|
Total | |||||||||
|
proiectii |
|||||||||
Sa se determine proiectia fluxului de numerar pentru urmatoarele 6 luni, cu ajutorul metodei celor mai mici patrate - hiperbola:
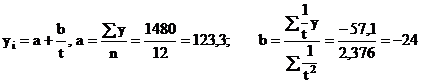 .
.
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 3298
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2025 . All rights reserved