| CATEGORII DOCUMENTE |
PIBefectiv/PIBnominal
PIB efectiv = rezultatul intersectiei CA-OATS
PIB potential = VAB ce se poate produce intr-o economie nationala in conditii de folosire dpeplina (optima) a factorilor de productial.
Consecinte:
La nivelul PIB potential avem rata naturala a somajului
Pe termen scurt PIB potential
Pe termen lung PIB potential descrie tendinta de crestere economica
Diferenta PIB potential - PIB efectiv = Decalaj de PIB (out-put gap)
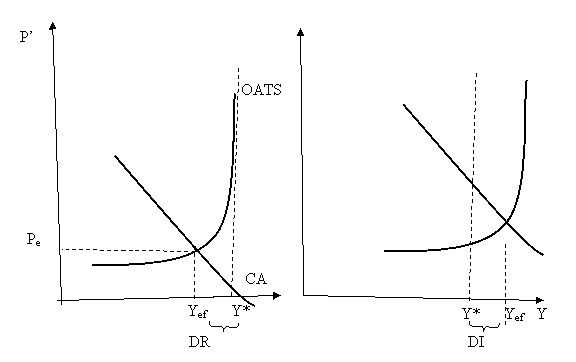
Fig. 1 Decalajele de rezultat macroeconomc (out-put gaps)
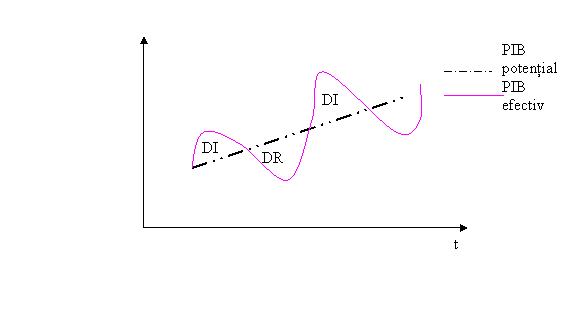
Fig. 2, Dinamica decalajelor macroeconomice
Variabille macroeconomice.
Y - aggregate out-put
Yef - effective out-put
Y* - potential out-put
Y* - potential out-put
Y = C + G + I + En
Y- (C+G) = I + En
YD = C + S
YD = Y + Tr - Ta => Y = YD - Tr + Ta
YD - Tr + Ta = C + G + I + En
C + S -Tr + Ta = C + G+ I + En
S- I = G + Tr - Ta + En

Fig. 3 CIRCUITUL MACROECONOMIC
S + (Ta -G -Tr) = I + En

CRESTEREA ECONOMICA
Motto:: Dun momentul in care cineva incepe sa se gandeasca la cresterea economica, ii va fi greu sa se mai gandeasca la altceva
Robert Lucas
Problema economica centrala: caracterizeaza performantele sistemului economic (national, mondial)
Corelare cu alte probleme macroeconomice majore:
Echilibrul
Ciclicitatea
Dezvoltarea economica
Definitie: Cresterea economica = evolutia ascendenta a rezultatului macroeconomic (PIB) potential.
Factori:
Resursele naturale
Stocul de capital
Inzestrarea tehnologica
Resursele umane → Capitalul uman
Cauzalitate si corelare factori Þ Modele de Crestere Economica
Modele Keynesiene:
Modelul lui Harrod. (1939)
Obiectiv: determinarea conditiile necesare pentru a se realiza o crestere echilibrata - cu deplina folosire a resurselor.
Studiaza consecintele pe termen lung ale modelului keynesian.
Roy Harrod arata ca disfunctionalitatile capitalismului semnalate de Keynes devin si mai mari intr-un orizont temporal cu mai multe perioade.
Chiar daca ar exista deplina folosinta la un moment dat, evolutia ulterioara a sistemului nu va mai mentine acest echilibru decat intamplator. Þ Necesitatea interventiei statului pentru asigurarea unei traiectorii de crestere echilibrate.
Considerand economisirea:
S = sY
Se presupune ca investitia este proportionala cu venitul:
I = vDY
Punand conditia de echilibru dintre investitie si economisire pentru fiecare perioada:
It = St Þ vDY = sYt Þ
DY/Yt = s/v
rata (ritm) de crestere, GW = s/v rata de crestere garantata (este data de doua marimi ce au tendinta sa se stabilizeze, constante; rata economisirii si inclinatia spre investire). In plus, aceasta rata garanteaza cresterea echilibrata (rezulta din conditiile de echilibru).
Egalitatea dintre investitia intentionata si investitia efectiva ca stare de echilibru presupune ca intreprinzatorii sunt multumiti si nu vor incerca modificarea conditiilor. Altfel spun atata timp cat economia creste cu o rata garantata investitorii isi vor pastra comportamentul (investitia intentionata = investitia realizata).
Presupunem acum ca economia nu creste cu o rata garantata. Þ Investitia efectiva ¹ investitia realizata, i. e. intreprinzatorii cresc productia mai rapid sau mai lent.
Caz I. G < GW Þ
Investitia intentionata < Economisire, Investitia efectiva
Deoarece investitia intentionata depinde de cresterea de venit. Þ o crestere neintentionata a obiectelor de inventar, i.e. o investitie neintentionata pozitiva:
Iinten < Ief Þ Ief = Iinten + dstoc-neint; d >
Dar, stocurile neintentionate implica neputinta intreprinzatorilor de a vinde intreaga productie. Astfel desi rata de crestere efectiva a output-ului < rata de crestere garantata, se pare ca intreprinzatorii au crescut productia prea rapid. Deoarece intreprinzatorii au impresia ca au crescut prea rapid productia Þ ca in perioada urmatoare ei vor incetini ritmul de crestere a productiei. Þ cresterea decalajului dintre ritmul efectiv si cel garantat in perioada urmatoare. s.a.m.d.
Caz II. G > GW Þ
Investitia intentionata > Economisire, Investitia efectiva
Aparenta pentru investitori ca nu au crescut suficient productia in raport cu cererea. Þ Vor creste aceasta productie si mai rapid s.a.m.d. Apar scurcircuite in utilizarea capacitatilor de productie.
Harrod crede ca odata ce s-a deviat de la ritmul garantat de crestere este dificil de stabilit echilibrul.
Incercand sa respecte ipoteza deplinei folosinte Harrod defineste
Gn ca rata (ritmul) naturala de crestere. Aceasta este ritmul de crestere maxim permis de cresterea in forta de munca, acumularea de capital si progresul tehnologic in concordanta cu deplina folosinta.
Din aceasta perspectiva cresterea echilibrata presupune tripla egalitate:
G = GW = Gn
Caci daca G = GW intreprinzatorii nu-si vor schimba comportamentul (nu se vor indeparta de echilibru), iar daca GW = Gn nu va exista somaj si inflatie.
Caci daca GW < Gn apare somaj.
Daca GW > Gn situatia nu poate dura din moment ce rata naturala este un prag maxim. Þ Se va reveni la rata naturala. Dar pentru aceasta rata efectiva trebuie sa scada Þ G < GW. Þ
Necesitatea adoptarii unor politici monetare si fiscale a.i. GW = Gn
Merite:
Introduce ideea de stabilizatori ai cresterii economice;
Coreleaza cresterea economica cu dinamica fortei de munca.
Critica
oFunctiile economisirii si investitiei sunt prea simple
Harrod zice ca se ajunge la acelasi rezultat si cu functii mai complicate.
Investitorii pot vedea decalajul dintre ritmul de crestere efectiv si cel garantat ca fiind temporar. (William Baumol). Ei isi pot mentine comportamentul Þ Decalajul devine mai mic, sau se resoarbe. Totusi daca decalajul se mentine mai multe perioade ei vor fi fortati sa modifice productia. Chiar si asa instabilitatea nu-i asa de grava.
Modelul nu ia in calcul substituibilitatea factorilor de productie (R. Solow). Daca preturile factorilor sunt flexibile si exista substituibilitate, deplina folosinta va preleva.
Modelul Domar (1946).
Obiectiv: dimensionarea fluxurilor de investitii necesare unei cresteri economice echilibrate.
Studiaza: problema deplinei folosinte pe termen lung (considerand un interval temporal cu mai multe perioade).
Punctul de plecare al modelului il reprezinta relatia multiplicatorului keynesian:
DY = DI/(1-c) (1)
Se considera ca economia se gaseste in situatia de deplina folosinta si cauta conditiile necesare ca aceasta stare sa se mentina si in perioadele urmatoare.
Cresterea potentiala este data si depinde de investitie si de o constanta s care exprima tehnicile existente.
Ipoteza deplinei folosinte presupune:
DI/(1-c) = Is (ecuatia fundamentala a lui Domar) (2) Þ
DI/I = s(1-c)
i.e. pentru a mentine deplina folosinta investitia trebuie sa creasca constant cu s(1-c) (cu ritmul s/s).
Domar sustine ca nu exista nici un motiv ca aceasta conditie sa fie verificata intr-o economie in care deciziile de investitii sunt luate descentralizat, de foarte multi intreprinzatori. Þ Echilibrul fara somaj nu poate fi atins decat in mod exceptional.
Concluzie: sistemul economiei de piata este departe de a conduce la echilibru deoarece cresterea necesara a capacitatilor de productie Is nu poate fi atinsa din moment ce deciziile de investitii sunt aleatorii si nu sunt corelate cu cresterea ofertei potentiale.
Chiar daca ar fi asa noile investitii se vor adauga la capacitatea de productie existenta, iar pentru mentinerea deplinei folosinte va fi nevoie de o crestere si mai accentuata si a investitiilor s.a.m.d.
Statul poate juca un rol esential in stimularea cererii chiar fara cresterea investitii. Aceasta deoarece in optica keynesiana ecuatia este valabila pentru cheltuiala autonoma, care nu influenteaza capacitatea de productie potentiala (oferta potentiala). Statul poate influenta inclinatia marginala spre consum in sensul cresterii modificand repartitia veniturilor si astfel sa franeze cresterea investitiilor necesara pentru mentinerea echilibrului deplinei folosinte (factorul (1-c)s scade).
Repartizarea veniturilor se poate face impozitand veniturile ridicate si subventionandu-le pe cele scazute.
Domar sustine ca sistemul economiei de piata tinde sa creeze capacitati de productie excedentare si ca doar interventia statului de a incuraja consumul poate tempera tendinta de spre suprainvestire.
Meritul principal: pericolul suprainvestitiilor. Economia Japoniei si Criza Asiatica (1996, 1997, 1998).
Critica. Modelul trateaza perioada interbelica, iar perioada de boom bazata pe cresterea cheltuielilor statului se refera mai ales la cheltuielile de razboi (efortul fiind oarecum o incordare disperata de forte). Modelul ar fi avut succes si dupa razboi cand cheltuielile statului erau directionate pentru refacerea economiei.
Modele ale Noilor Economisti Clasici:
Consideratii preliminare: Majoritatea modelelor de crestere economica lucreaza cu functii de productie care au ca variabile stocul agregat de capital si volumul agregat de munca. Diferentierea dupa forma acestei functii se face in functie de influenta progresului tehnologic:
Y = F(K,AL) - cu progres tehnologic crescator in munca, Harrod - neutral
Y = F(AK,L)
- progresul tehnologic
Y = AF(K,L)
- progresul tehnologic
MODELUL LUI SOLOW (1956)
Reprezinta punctul de plecare pentru aproape toate analizele privind cresterea economica. In plus alte abordari sunt mai usor de inteles daca se face referire la acest model.
Ipoteze:
1. Ipoteze privind functia de productie:
Functia de productie are randamente de scara constante, i.e. c > o , avem: F(cK, cAL) = cF(K,AL), caci:
economia este suficient de mare pentru ca posibilitatile de specializare sa fie aproape epuizate; economii mici pot exista posibilitati
alte intrari in afara de munca, capital si cunoastere sunt neimportante. (resursele naturale nu-s o problema pentru tarile dezvoltate).
Ø Timpul nu reprezinta intrare directa in functia de productie, ci numai prin K, L, si A. => Y schimbari numai daca in factorii de productie apar schimbari.
Se lucreaza cu o forma simplificata a functiei de productie, forma intensiva, considerand:
![]() =>
=> ![]() (1)
(1)
Se definesc:
![]() - volumul de capital pe unitatea de munca
efectiva,
- volumul de capital pe unitatea de munca
efectiva,
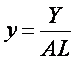 - outputul (rezultatul
macroeconomic) pe unitatea de munca efectiva
- outputul (rezultatul
macroeconomic) pe unitatea de munca efectiva
f(k) = F(k, 1) => din (1) y = f(k) (2).
Legatura dintre y si Y
Y = ALf(k).
Forma intensiva a functiei de productie, f(k), satisface urmatoarele proprietati (Inada):
f(0) = 0; f'(k) > 0; f''(k) < 0; f'(0) = f'(
2. Evolutia stocurilor de capital, munca si cunostinte
L'(t) = nL(t); A'(t) = gA(t) (3)
n, g - parametrii
exogeni, iar ![]()
N.B. Relatiile de mai sus pot fi exponentiale,
L(t) = L(0)ent, A(t) = A(0)egt.
Partea din venitul agregat (output) destinata investitiei este considerata exogena si constanta, s, iar rata uzurii capitalului este d. Astfel:
![]() (4)
(4)
Singura restrictie este ca parametrii, n+g+d > 0
Dinamicile modelului:
Dinamica lui k
Din moment ce functia de productie este crescatoare in k, rezulta necesitatea studierii variabilei k.
Prin transformari succesive a ecuatiei (4) se obtine o forma intensiva pentru dinamica lui k:
![]() (5)
(5)
- ecuatia principala a modelului lui Solow.
Ecuatia arata ca rata de modificare a stocului de capital/unitatea de munca efectiva este egala cu diferenta dintre: s*f(k) - investitia reala/unitatea de munca efectiva si
(n+g+d)k(t) - investitia punctului critic, i.e. volumul investitiei care trebuie facuta doar pentru a pastra pe k la nivelul existent.
Exista doua motive pentru care sunt necesare ceva investitii pentru a preveni caderea lui k:
uzura capitalului existent si cresterea cantitatii de munca efectiva.
Chiar daca investitia asigura pastrarea constanta a stocului de capital K, aceasta nu-i suficient pentru pastrarea lui k constant.
Cand investitia/unitatea de munca efectiva depaseste investitia pragul critic al k creste, de nu k scade (vezi figura nr.1).
Fie k* solutia ecuatiei k'(t) = 0, corespunzatoare maximului lui k. Se
poate observa ca exista o relatie intre k'(t) si k(t). ![]()
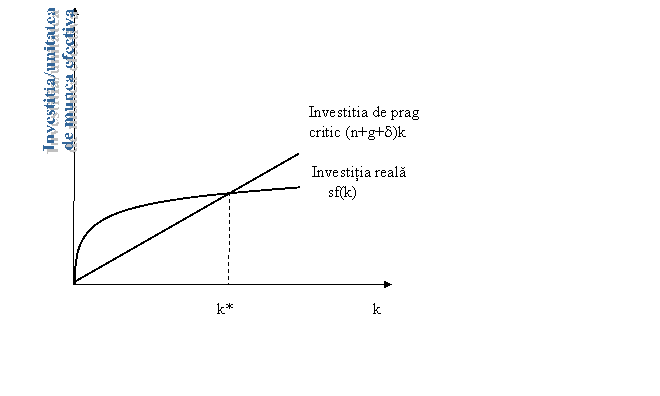 Fig. 1. Investitia reala
si de prag critic.
Fig. 1. Investitia reala
si de prag critic.
Realizand o translatie convenabila se poate obtine urmatoarea diagrama de faza pentru k (fig. 2)
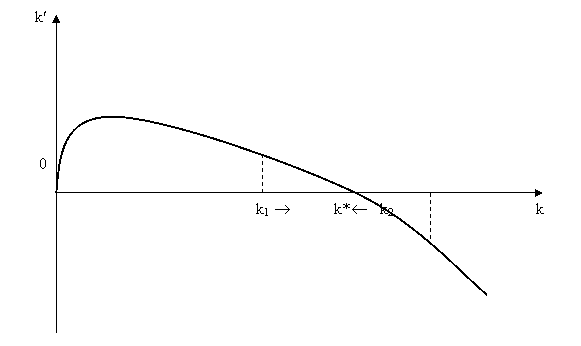
Fig. 2. Diagrama de faza a modelului Solow
Daca, initial k1 < k*, => investitia reala depaseste investitia de prag critic, => k' > 0, i.e. k creste.
Daca, k2 > k* => k¢ < 0.
Pt k = k* => k' = 0 (k nivel maxim).

Calea de crestere echilibrata
Din moment ce k tinde (converge) spre k* => intrebarea:
cum se comporta variabilele modelului pentru k = k*.
Prin definitie munca si cunoasterea cresc in ratele n si g (vezi ecuatiile de start). Stocul de capital K = ALk*; din moment ce k este constant (=k*), K va creste cu rata n+g (i.e. K'/K = n+g). Daca atat capitalul cat si munca efectiva cresc cu rata n+g, din conditia de randamente de scara constante => ca si Y creste cu aceiasi rata.
In final, capitalul/lucrator (inzestrarea tehnica a muncii), K/L, si productia pe lucrator, Y/L, cresc cu rata g.
Astfel, modelul lui Solow implica faptul ca indiferent de punctul de start, economia converge spre o cale de crestere echilibrata - o situatia unde fiecare variabila a modelului creste cu o rata constanta.
Pe o astfel de cale de crestere, rata de crestere a output/lucrator este determinata numai de rata progresului tehnic - g
In cele mai multe tari dezvoltate, se poate aproxima oarecum, ca ratele de crestere ale capitalului, muncii si productiei au fost oarecum constante.
Impactul modificarii ratei de economisire
Parametrul din modelul Solow care este cel mai succeptibil influentelor de politica economica este rata de economisire (s). Impartirea achizitiilor guvernamentale intre bunuri de consum si bunuri de investitii; a veniturilor intre taxe si imprumuturi si a modului in care sunt tratate economisirea si investitia, este foate posibil sa afecteze partea din venitul agregat care este investita.
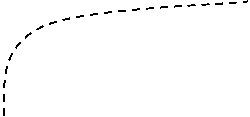
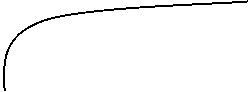
Cresterea lui s ridica curba investitiei reale, => k* creste. Dar, k nu sare imediat la noua valoare a lui k* (vezi fig. 3).
Initial k = vechea valoare a lui k*. La acest nivel, investitia reala depaseste acum investitia de prag critic - i.e. este alocat un volum de investitie peste cel necesar mentinerii constante a lui k - si astfel k' > 0. => k incepe sa creasca si va continua sa creasca pana ce va intanli noul prag k*, unde va ramine constant.

![]() (n+g++d)k
(n+g++d)k
![]()
![]()
![]()
![]()
![]() snf(k)
snf(k)
![]()
 svf(k)
svf(k)
![]() k*v k*n
k*v k*n
Fig. 3. Efectul unei cresteri a ratei economisirii asupra investitiei.
Cat priveste output/lucrator Y/L, atunci cand k este constant, aceasta creste in ritmul g (rata lui A). (Y/L = Af(k)).
Cand k creste, Y/L creste si datorita lui A si a lui k. Rata de crestere a lui k depaseste pe g. Dar cand k devine = k*, din nou cresterea lui Y/L este datorata doar lui g. =>
ca o crestere permanenta a ratei economisirii produce doar o crestere temporara a ratei de crestere a productiei pe lucrator (alminteri ea este constanta la nivelul g): k creste doar un timp, dar la un punct unde economisirea suplimentara este necesara in intregime pentru a mentine nivelul ridicat a lui k. (vezi figura 4)
![]()
![]()
![]() s
s
![]()
t0 t
![]() k
k
![]()
![]() t0 t
t0 t
Rata
![]()
![]() crest
crest
![]()
![]() Y/L
Y/L
![]()
![]() g
g

t0 t
lnY/L

![]() t0 t
t0 t
Fig. 4 Efectele unei cresteri in rata economisirii
t0 - momentul cresterii ratei de economisire.
Prin ipoteza s sare la momentul t0 si ramane constanta la acest nivel.
k creste gradual de la vechea valoare k* la noua valoare. Rata de crestere a productiei/lucrator, ce era initial g, va creste in momentul t0, si apoi va reveni gradual la vechiul nivel.
In concluzie, modificarea lui s are un efect de nivel, dar nu un efect de crestere: aceasta va modifica calea de crestere echilibrata a economiei, si astfel nivelul productiei/lucrator la orice moment de timp, dar nu va afecta rata de crestere a productiei/lucrator pe calea de crestere echilibrata.
In modelul lui Solow numai schimbarile in rata progresului tehnologic au efecte de crestere, celelalte au doar efecte de nivel.
Impactul asupra consumului
Aceasta presupune introducerea gospodariilor in model: bunastarea lor depinde de consum nu de productie, iar investitia este o problema de viitor.Initial consumul va descreste brusc apoi va creste pe masura cresterii lui k si a mentinerii lui s la noul nivel. (fig. 1.5).
![]() c
c
![]()
![]()
t0 t
Efectul asupra productiei agregate pe termen lung.
Efectul pe termen lung a unei cresteri a lui s asupra productiei agregate, este dat de
y*/ s = f'(k*) k*(s,n,g,d s (1.16)
y = f(k*) - nivelul productiei/unitatea de munca efectiva pe o cale de crestere echilibrata. Astfel pentru a gasi y*/ s, este necesar sa fie aflat k*/ s. Pentru aceasta se reaminteste ca k* este definit a.i. k' = 0, => k* satisface relatia:
sf(k*(s,n,g, d)) = (n+g+d k*(s,n,g, d (1.17)
Unde k*f'(k*)/f(k*) - elasticitatea productiei in raport cu capitalul k*, notata
ak(k*) =>
i.e. daca pietele sunt competitive si nu exista externalitati, capitalul atinge productivitatea sa marginala. In acest caz, volumul total primit de capital (/unit de munca efectiva)pe o cale de crestere echilibrata este k* f'(k*). Astfel daca acest capital atinge productivitatea sa marginala, partea din venitul agregat care revine capitalului este k* f'(k*)/f(k*) (sau ak(k*)).
In cele mai multe tari, partea de venit ce revine (este platita) capitalului este de circa o treime. Daca utilizam aceasta data in estimarea lui ak(k*) => ca elasticitatea productiei in raport cu rata economisirii pe termen lung este de circa 1/2. De exemplu, pt o crestere de 10% a ratei economisirii (de la 20% la 22%). produce o crestere a productiei pe lucrator de circa 5% in raport cu calea care ar trebui sa fie urmata. Chiar la o crestere de circa 50% in s, y* numai de 22% crestere. =>
modificari insemnate in rata econmisirii au doar un efect moderat asupra nivelului productiei pe o cale de crestere echilibrata
Viteza de convergenta
In practica, noi suntem interesati nu numai de eventualele efecte asupra modificarii unor parametri (cum ar fi s) ci si de rapiditatea cu care se petrec aceste efecte.
In mod normal n+g+d este de circa 6% (1-2% pt cresterea populatiei, 1-2% pentru cresterea output/lucrator, 3-4% pt uzura). Daca partea capitalului este de circa 1/3, (1- ak) (n+g+d) este de circa 4% . Prin urmare k si y se misca cu 4% anual si sunt necesari aproximativ 18 ani pentu a atinge calea de mijloc a valorilor caii de crestere echilibrata. De exemplu, la o crestere a lui s de 10%, output este 0.04(5%) = 0.2% peste calea prevazuta dupa un an; este de 0,5(5%) = 2.5% peste traiectorie, dupa 18 ani, va atinge 5% asimptotic. =>
Nu numai ca impactul modificarii lui s sunt modeste, dar si viteza de producere este slaba.
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 1435
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2025 . All rights reserved