VALOAREA IN TIMP A BANILOR

valoarea in timp a banilor

Multe decizii financiare se refera la situatii in care o persoana fizica sau juridica efectueaza anumite plati la un moment in timp si primeste fonduri la un alt moment. Banii care se platesc sau se incaseaza la momente diferite in timp au valori diferite, iar aceasta diferenta de valoare este recunoscuta si denumita analiza valorii in timp a banilor.

Un dolar disponibil in prezent este mai valoros decat acelasi dolar ce va fi primit candva in viitor, deoarece, daca dolarul este disponibil in prezent, el poate fi investit si astfel se poate castiga o suma mai mare decat un dolar in viitor. Procesul prin care se ajunge de la valorile prezente ("present values") la valorile viitoare ("future values") ale unei sume de bani se numeste compunere.

Vom defini in continuare cativa termeni pentru a putea explica acest proces:

VP = valoarea prezenta (disponibila in momentul actual);

k = rata dobanzii anuale de care se beneficiaza pentru suma depusa;

S = suma castigata din dobanda intr-un an, sau S = VP* k pentru primul an;

VV_n = valoarea viitoare, valoarea acumulata sau valoarea finala a sumei initiale peste "n" perioade de timp, de regula ani;

n numarul de perioade de timp.

La sfarsitul unei perioade sau an, vom obtine:

VV₁ = VP+S = VP+VP*k = VP(1+k),

iar daca rationamentul continua:

VV₂ = VV₁+S = VV₁+VV₁*k = VP(1+k)+VP(1+k)*k = VP(1+k)².

Atunci, la sfarsitul a "n" ani sau perioade, valoarea finala sau viitoare, VV_n, se calculeaza astfel: VV_n = VP(1 + k)ⁿ, adica este valoarea initiala (prezenta) multiplicata cu 1 plus rata dobanzii pe intreaga perioada considerata. Termenul (1 + k)ⁿ se numeste factor de compunere sau factor de fructificare.

Acum, sa presupunem ca in viitor, la sfarsitul a "n" perioade, valoarea finala a unei sume initiale va fi VV_n, iar rata dobanzii anuale este k.

Atunci, valoarea initiala, prezenta, VP, a fost de: VP=VV_n / (1+k)ⁿ. In acest caz, termenul 1/(1+k)ⁿ se numeste factor de actualizare, deoarece el permite cunoasterea valorii prezente, actualizate, sau a capitalului initial care s-a transformat, peste "n" perioade, in suma finala VV_n. Se observa ca factorul de actualizare este inversul factorului de fructificare.

In general, valoarea prezenta - VP ("present value") a unui flux de numerar, platibil dupa "n" ani in viitor, este reprezentata de suma care, daca ar fi disponibila in momentul prezent, va creste, astfel incat sa atinga valoarea respectiva in viitor.

Concluzionand, procedeul de compunere este procedeul de determinare a valorii viitoare a unui flux de numerar sau a unei serii de fluxuri de numerar, valoare viitoare care este egala cu suma initiala plus dobanda acumulata, iar gasirea valorii prezente a unui flux de numerar viitor - procedeu numit actualizare ("discounting") - este pur si simplu inversul operatiei de compunere.

Sa presupunem acum ca suma prezenta VP este plasata pe durata de timp

n=t₁+t₂+.+t_n si ca pe fiecare perioada t_i procentul anual de dobanda este k_i. Atunci, suma finala VV_n corespunzatoare acestui plasament este: VV_n = VP(1+k₁t₁)(1+k₂t₂)..(1+k_nt_n), unde t_i este exprimat in ani. In acest caz, factorul de fructificare este (1+k₁t₁ 1+k₂t₂)..(1+k_nt_n), iar inversul sau este factorul de actualizare. Daca perioadele t_i sunt egale cu 1 an, atunci VV_n=VP(1+k₁)(1+k₂).(1+k_n).

valoarea viitoare a unei serii de fluxuri de numerar

O serie de fluxuri de numerar ("cash-flow-uri") se poate caracteriza prin fie prin fluxuri constante de-a lungul perioadei considerate, fie prin fluxuri inegale. Cu toate ca exista numeroase decizii financiare care se materializeaza in fluxuri de numerar constante, unele decizii foarte importante, cum ar fi de exemplu investitiile in active fixe, nu genereaza, in mod normal, fluxuri constante de numerar. Pentru cash-flow-uri egale, se particularizeaza pur si simplu formula pentru calculul valorii viitoare a fluxurilor inegale.

Valoarea viitoare a unei serii de fluxuri de numerar inegale - valoare care se mai numeste uneori valoare terminala ("terminal value") - se determina prin procedeul de compunere al fiecarui cash-flow al seriei si prin insumarea ulterioara a acestor valori viitoare.

De exemplu, sa consideram o axa temporala, unde reprezentam timpul, cu momentul actual si cel final al perioadei considerate. De asemenea, vom inscrie si rata de compunere, k, si cash-flow-urile corespunzatoare fiecarei perioade, considerate la sfarsitul perioadei, CF_t: Atunici, valoarea viitoare pentru o serie de cash-flow-uri inegale este data de relatia:

VV_n =

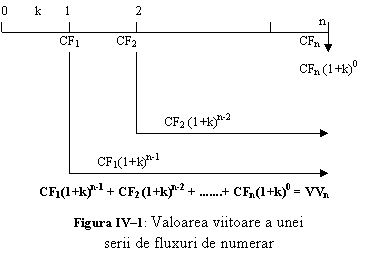
De obicei, intereseaza mai mult valoarea prezenta a unei serii de fluxuri de numerar produse de un activ decat cea viitoare, deoarece valoarea prezenta reprezinta valoarea din momentul actual, pe care o putem compara cu pretul activului.

valoarea prezenta a unei serii de fluxuri de numerar

Valoarea prezenta VP a unei serii de fluxuri de numerar inegale se determina ca suma a valorilor prezente ale diferitelor componente ale seriei. Valoarea prezenta poate fi gasita prin aplicarea ecuatiei generale a valorii prezente:

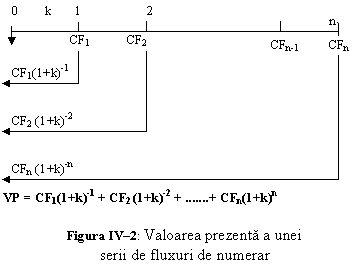
VP =