Cercetarea statistica prin sondaj (metoda de baza in studiul fenomenelor sociale si economice)

CERCETAREA STATISTICA PRIN SONDAJ (METODA DE BAZA IN STUDIUL FENOMENELOR SOCIALE SI ECONOMICE)

Pentru caracterizarea statistica a fenomenelor si proceselor social-economice de masa, cu scopul evidentierii legitatilor specifice acestora se folosesc date individuale obtinute prin metode de inregistrare totala sau partiala.

In conditiile economico-socialesocio-economice actuale, din nevoia de informatii rapide, complexe, metoda principala de obtinere a informatiilor statistice este aceea a sondajului statistic.

Procesul cuprinde doua etape:

etapa descriptiva in care se culeg date si se calculeaza indicatorii ce caracterizeaza subcolectivitatea analizata;

etapa inferentiala in care rezultatele obtinute pentru aceasta subcolectivitate, se extind, in termeni probabilistici, la colectivitatea generala.

Avantajele cercetarii prin sondaj:

reducerea costurilor materiale si de munca;

erorile de inregistrare sunt mai putin numeroase si mai usor de inlaturat in faza de verificare a datelor;

programul observarilor prin sondaj cuprinde un numar mai mare de caracteristici decat programul observarii totale, ceea ce permite caracterizarea mai aprofundata a fenomenelor studiate prin metode statistice;

sondajul poate fi utilizat cu bune rezultate la verificarea programului unei observari totale, cat si la verificarea unor ipoteze statistice

Definitie: Selectia statistica reprezinta operatia de extragere a unei parti dintr-o colectivitate statistica, a unei subcolectivitati numita si esantion, mostra, colectivitate partiala sau colectivitate de selectie.

Volumul esantionului este intotdeauna mai mic decat cel al colectivitatii generale.

Notam: volumul colectivitatii generale cu N si volumul colectivitatii de selectie cu n, atunci .

In cazul in care datele au fost sistematizate in r grupe, dupa variatia unei caracteristici de grupare, avem:

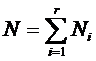
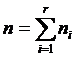
Atunci cand toate elementele unei colectivitati sunt masurate, orice indicator statistic ce caracterizeaza repartitia statistica se numeste parametru. Pentru datele provenite dintr-un esantion, indicatorul statistic calculat se numeste estimator.

Indicatorii tendintei centrale si cei ai variatiei vor avea notatii diferite, dupa cum ei sunt obtinuti dintr-o cercetare statistica totala sau partiala. Astfel, media aritmetica va fi notata cu μ in cazul unei colectivitati totale si cu in cazul in care este un indicator obtinut printr-o cercetare statistica prin sondaj.

Parametrul colectivitatii generale se calculeaza astfel:

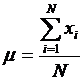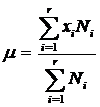sau unde

Estimatorul parametrului obtinut pentru esantion:

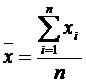sau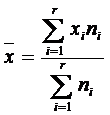

Dispersia se va nota cu σ² daca este parametru obtinut in colectivitatea generala si cu s² daca este estimatorul parametrului, obtinut pe un esantion.

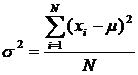sau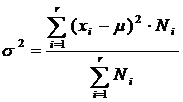

Dispersia esantionului:

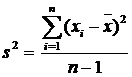sau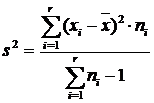

Observatie:

Rezolvarea problemelor cuprinse in planul de sondaj are drept scop asigurarea reprezentativitatii esantionului, de aceasta depinzand in totalitate valoarea rezultatelor obtinute in urma cercetarii.

1. PROCEDEE DE ESANTIONARE

Metoda selectiei aleatoare sta la baza oricarei esantionari, in vederea obtinerii unei inferente statistice. Procedeele de esantionare se aplica pentru a reduce erorile de selectie.

In selectia aleatoare se disting urmatoarele tipuri de sondaj:

sondaj simplu aleator;

sondaj tipic (stratificat);

sondaj pe serii (cuiburi);

sondaj pe mai multe trepte;

sondaj secvential.

Sondajele pot fi repetate sau nerepetate, dupa cum exista posibilitatea revenirii unei aceleiasi unitati in cadrul aceluiasi esantion, astfel, in esantionul repetat, sau, cu revenire, fiecare unitate statistica extrasa din colectivitatea generala este reintrodusa in baza de sondaj dupa ce a fost citita si caracteristicile au fost inregistrate. In varianta sondajului nerepetat (fara revenire) unitatile sunt extrase din colectivitatea generala, iar dupa inregistrarea lor ele nu mai sunt reintroduse in colectivitatea de baza; selectia se face dupa modelul urnei din care se fac extrageri succesive, fara a pune inapoi bila extrasa, iar o unitate nu poate sa apara decat o singura data.

Extragerea intamplatoare a unitatilor si alcatuirea esantioanelor aleatoare se poate realiza prin:

procedeul urnei cu bile (procedeul loteriei);

procedeul tabelului cu numere intamplatoare;

procedeul mecanic.

Procedeul urnei cu bile poate fi realizat in varianta cu revenire sau in varianta fara revenire. Colectivitatea generala este numerotata de la 1 la N. Numerele sunt notate pe bile (cartonase) si sunt amestecate atent. In varianta cu revenire bila (cartonasul) este reintrodusa in urna, se repeta amestecarea, extragerea se repeta pana la obtinerea esantionului de volum n. Probabilitatea ca o unitate sa fie extrasa este 1/N, iar dupa ultima extragere din urna raman (N-1) bile. Numarul esantioanelor distincte de volum n ce pot fi extrase in sondajul cu revenire este Nⁿ. In varianta fara revenire, dupa extragerea primei bile in urna raman (N-1) bile, dupa a doua extragere (N-2) bile, astfel incat, dupa ultima extragere, in urna raman (N-n) bile, unde n este volumul esantionului. Probabilitatea unei bile de a fi aleasa in esantion creste, astfel la extragerea cu numarul i, , probabilitatea unei unitati de a fi selectata este 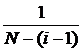. Numarul de esantioane distincte, de volum n, ce pot fi extrase este .

Procedeul tabelului cu numere intamplatoare consta in prelevarea din cadrul populatiei a unitatilor ale caror numere de ordine stabilite printr-o numaratoare prealabila au fost citite dupa un anumit criteriu din tabelul numerelor aleatoare. Tabelul este o lista de numere in care fiecare cifra, de la 0 la 9, apare cu o probabilitate de 1/10 independent una de alta.

Elementul colectivitatii generale se numeroteaza de la 1 la N, astfel incat sa nu ramana nici un element nenumerotat si sa nu se repete acelasi numar. Se selecteaza apoi un loc de unde incepe citirea numerelor din tabelul cu numere intamplatoare. Se organizeaza numerele citite in grupuri de cifre a caror marime este numarul de cifre continut de numarul N. Numerele astfel formate identifica unitatile statistice care sunt selectate in esantion daca sunt cuprinse intre 1 si N. Daca un numar este zero sau mai mare de N, el este eliminat, deoarece nu exista o unitate corespunzatoare in colectivitatea generala care sa fie selectata. Citirea continua pana cand se selecteaza n unitati statistice.

Exemplu:

Sa alegem un esantion aleator de n = 7 unitati dintr-o colectivitate de 38 unitati, incepand cu randul 10, coloana 2 din tabelul cu numere aleatoare. Numerele citite din tabel vor fi:

Cum N = 38 are doua cifre, se rearanjeaza secventa citita in grupuri de cate doua cifre astfel:

Se elimina numerele mai mari de 38:

Daca selectia este fara revenire se elimina numerele care reapar in lista:

1.1. Sondajul aleator simplu repetat

Pe baza valorilor observate x₁, x₂, ,x_n in esantionul aleator simplu de volum n, extras dintr-o colectivitate generala de volum N, media de sondaj:

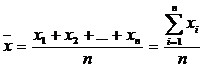
si este un estimator nedeplasat al mediei μ din colectivitatea generala.

Dispersia mediilor de selectie este de n ori mai mica decat dispersia colectivitatii generale si se estimeaza pe baza dispersiei esantionului

Eroarea medie de reprezentativitate (abaterea medie patratica a mediei de sondaj) se determina pe baza datelor din esantion ca

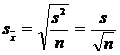
Deoarece am extras un esantion de volum n dintr-o colectivitate generala de N unitati putem constitui un interval de incredere, cu o probabilitate de 100(1-α) la suta de garantare a rezultatelor, pentru parametrul media colectivitatii generale (μ).

Observatie: Un esantion se considera de volum normal sau mare daca n>30 unitati statistice.

Pentru a construi acest interval de incredere, determinam eroarea limita maxima admisibila stiind ca media de sondaj este variabila aleatoare normal distribuita de medie, μ rezulta variabila normala normata corespunzatoare este .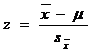

Pentru probabilitatea cu care se garanteaza rezultatele 100(1-α)%, eroarea limita (maxima) admisibila este:

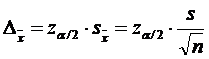
adica in 100(1-α)% din cazuri, media de sondaj se abate de la media colectivitatii generale μ cu mai putin sau cel mult z _{α / 2} ori eroarea medie de reprezentativitate .

Intervalul de incredere calculat pe baza erorii limita admisibila este:

, si va contine valoarea adevarata a mediei din colectivitatea generala μ in 100(1-α)%.

Observatie: Cea mai folosita probabilitate de garantare a rezultatelor este de 95% pentru care z _0,025 = 1,96, adica P (-1,96 < z < 1.96) = 0,95

Exemplu: Sa se determine intervalul de incredere, garantat cu o probabilitate de 95% pentru media si nivelul total al unei caracteristici numerice X, daca esantionul selectat aleator repetat este de 36 de unitati (adica, 5% din colectivitatea generala), de medie 800 si abatere medie patratica 60.

Cum n = 36 > 36 (esantion de volum normal sau mare) intervalul de incredere pentru media in colectivitatea generala este dat de ,

n = 36, = 800,

s = 60,

1 α = 0,95

z_0,025 = 1,96

eroarea medie de reprezentativitate este :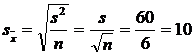

eroarea limita maxima admisibila:

Intervalul de incredere pentru parametrul colectivitatii generale este dat de:

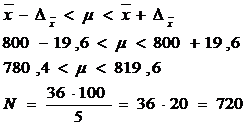
pentru nivelul total al caracteristicii studiate: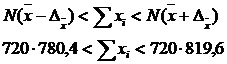

Aceste intervale sunt garantate cu o probabilitate de 95% ceea ce inseamna ca exista un risc de 5% ca media din colectivitatea generala sa aiba o valoare mai mica de 780,4 sau mai mare de 819,6, iar nivelul total al variabilei sa nu se incadreze in intervalul (561888, 590112).

1.1.1. Determinarea volumului esantionului

Pornind de la eroarea limita maxima admisibila, cu un nivel de incredere (1 - α), adica o probabilitate de garantare a rezultatelor 100 (1 α)%, volumul necesar al esantionului se determina rezolvand ecuatia:

ridicam la patrat

Solutia poate fi scrisa ca:

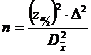
Exemplu: Sa se determine volumul esantionului necesar pentru a estima media unei colectivitati μ cu o eroare limita de 0,2 si o probabilitate de garantare a rezultatelor de 95%, stiind dintr-o cercetare anterioara ca dispersia Δ² este aproximativ egala cu 6,1 unitati statistice.

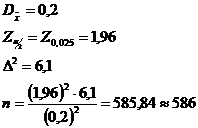
1.2. Sondajul aleatoriu simplu nerepetat

Daca N este volumul colectivitatii generale, atunci P(x₁=x₁)=, , cu alte cuvinte, probabilitatea evenimentului x₂=x₂ se schimba dupa cum evenimentul x₁=x₁ a avut sau nu loc.

Dispersia mediei de selectie este si estimata prin .

Abaterea medie patratica a mediei de selectie (eroarea mediei de reprezentativitate) este si estimata prin ; se numeste coeficient de corelatie finita in populatie iar raportul reprezinta fractia de sondaj.

Observatie: Pentru in calcule nu se ia in considerare.

Eroarea limita maxima admisibila in cazul sondajului fara revenire este: .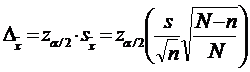

Intervalul de incredere pentru media μ din colectivitatea generala corespunzator probabilitatii 100(1-α)% de garantare a rezultatelor este: .

Exemplu: Un esantion aleator de 80 de observatii a fost selectat nerepetat dintr-o populatie normal distribuita de volum N = 800 de unitati. In urma calculelor =14,1 si abaterea medie patratica s = 2,6. Sa se determine intervalul de incredere, garantat cu o probabilitate de 95% pentru media colectivitatii generale μ.

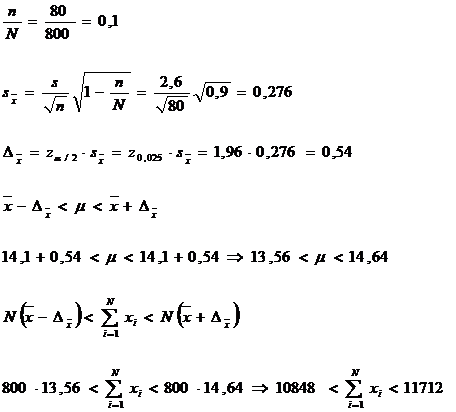
1.2.1. Determinarea volumului esantionului

In cazul sondajului aleatoriu simplu nerepetat, pentru determinarea volumului esantionului (n) pornim de la formula erorii limita maxima admisibila.

ridicam la patrat

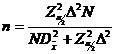
Exemplu. Un esantion aleatoriu a fost selectat nerepetat dintr-o populatie normal distribuita de volum N = 800 unitati. In urma calculelor a rezultat eroarea limita de 0,3 si abaterea medie patratica s = 2,6. Sa se determine volumul esantionului, garantat cu o probabilitate de 95%.

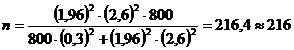unitati statistice

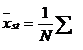
Dispersia mediei

Obtinem estimatorul dispersiei mediei de selectie

si eroarea medie de reprezentativitate (abaterea medie patratica)

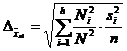
Daca fractia de sondaj este uniforma pentru toate straturile (selectie stratificata proportionala) atunci si expresia erorii medii de reprezentativitate devine:

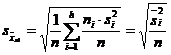
reprezinta media dispersiilor de grupa din esantion

Eroarea limita maxima admisibila

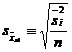
Intervalul de incredere pentru media colectivitatii generale este dat de:

Determinarea volumului esantionului se va efectua pornind de la formula erorii limita maxima admisibila.

2. Alegeti raspunsul corect

1. Intr-o cercetare prin sondaj, valoarea medie la nivelul unei populatii reprezinta:

a. un parametru;

b. o valoare tipica de sondaj;

c. un estimator;

d. o estimatie.

2. Formarea esantionului in cazul unui sondaj aleatoriu simplu presupune ca:

a. fiecarui individ din populatie sa i se asocieze o probabilitate egala sau inegala, de a intra in esantion;

b. esantionul sa se formeze prin extragerea unui numar de grupe;

c. esantionul sa se formeze prin extragerea aleatoare a unitatilor la nivelul fiecarei grupe.

3. In cazul sondajului stratificat (tipic) simplu, esantionul se formeaza extragand din fiecare grupa omogena a colectivitatii generale:

a. acelasi numar de unitati, indiferent de ponderea fiecarei grupe in colectivitate;

b. un numar de unitati proportional cu ponderea grupelor in colectivitatea generala;

c. un numar de unitati proportional cu ponderea grupelor in colectivitatea generala si gradul de dispersie din grupe.

4. Erorile de reprezentativitate reprezinta diferente intre:

a. valoarea estimata si valoarea adevarata a unui parametru;

b. valorile reale si valorile inregistrate;

c. populatia reala si esantionul observat.

5. Selectia statistica reprezinta:

a. extragerea unei colectivitati dintr-un esantion;

b. Extragerea unei parti dintr-o colectivitate generala;

c. compararea datelor a doua colectivitati.

6. Volumul unui esantion trebuie sa fie:

a. intotdeauna mai mic decat colectivitatea generala;

b. Intotdeauna mai mare decat colectivitatea generala;

c. egal cu colectivitatea generala.

	3. Probleme

1. Cunoastem urmatoarele date la nivelul unei populatii:

N = 200 persoane, .

Admitem o precizie si un risc , pentru care z = 1,96.

Se cere sa se calculeze volumul esantionului corepunzator unui sondaj aleator simplu repetat, interpretati rezultatul.

2. Dispunem de urmatoarele date la nivelul unei populatii:

N = 400 persoane, .

Admitem o precizie si u risc , pentru care z = 1,96.

Se cere sa se calculeze volumul esantionului corespunzator unui sondaj aleator simplu nerepetat. Interpretati rezultatul

3. Pentru un sondaj aleator simplu nerepetat, realizat asupra unui esantion de volum n= 100, extras dintr-o populatie de volum N = 1000, s-au obtinut = 40 ani, s= 22 ani. (s= dispersia esantionului).

Pentr un (nivel de semnificatie), valoare erorii medii de selectie este:

a)     2,2

b)     2,0856

c)     4,312

4. Se extrage un esantion aleatoriu simplu repetat de volum n= 900 persoane, s-au obtinut urmatoarele rezultate:

= 5 milionane lei.

s = 3 milioane lei.

Considerand un risc de 5 %, sa se afle limitele intervalului de incredere pentru media populatiei din care s-a extras esantionul:

a) (4,732; 5,653)

b) (4,653; 5,789)

c)  (4,904; 5196)

5. Pentru un sondaj aleator simplu repetat, realizat asupra unui esantion de volum

n= 100, valoarea mediei esantionului si valoarea abaterii medii patratice (s) sunt:

= 30 ani

s = 3 ani

Pentru un = 0,05, valoarea erorii limita de selectie este:

a)     0,3

b)     0,588

c)     30

6. Pentru un sondaj aleator simplu nerepetat, realizat asupra unui esantion de volum n=25, extras dintr-o populatie de volum N=1000, s-au obtinut:

= 40 ani; s=22 ani;

Pentru un =0,05, valoarea erorii medii de selectie este:

a.     2,2

b.     2,0856;

c.      4,312

	4. Raspunsuri corecte

2. Raspunsuri corecte.

1. a. un parametru;

2 a. fiecarui individ din populatie sa i se asocieze o probabilitate egala sau inegala, de a intra in esantion;

3. a. acelasi numar de unitati, indiferent de ponderea fiecarei grupe in colectivitate;

4. a. valoarea estimata si valoarea adevarata a unui parametru;

5. b. Extragerea unei parti dintr-o colectivitate generala;

6. a. Intotdeauna mai mic decat colectivitatea generala;

3. Raspunsuri corecte.

1. Raspuns. Volumul esantionului corespunzator unui sondaj aleator simplu repetat se calculeaza dupa relatia:

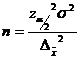
n=

Interpretare: numarul persoanelor care ar trebui extrase aleatoriu simplu repetat din populatia de volum N 0 200 este de 20,17 20 persoane.

2. Raspuns. Volumul esntionului corespunzator unui sondaj aleator simplu nerepetat, se calculeaza dupa relatia:

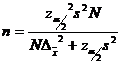
n=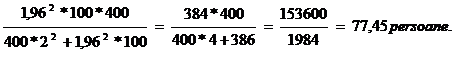

Interpretare: numarul persoanelor care ar trebui extrase aleatoriu simplu si nerepetat din populatia de volum N =400 este de 77,45 77 persoane.

1.     Raspuns. b) Eroarea medie de selectie (reprezentativitate) se calculeaza dupa formula:

2. Raspuns: c) Considerand un risc de 5%, limitele intervalului de incredere pentru media populatiei din care s-a extras esantionul sunt:

3. Raspuns: b) Pentru un sondaj aleator simplu repetat, valoarea erorii limita de selectie , pentru un nivel de semnificatie este:

6. Raspuns b) =