Testarea parametrilor variabilelor calitative

In capitolul anterior am tratat teste utilizate pentru verificarea ipotezelor privind mediile populatiilor. De foarte multe ori variabilele din planul de observare al cercetarilor din sfera economica nu pot fi masurate cardinala sau proportionala. Pentru variabilele calitative indicatorul sintetic utilizat se calculeaza ca o proportia in populatie (sau esantion) a celor care indeplinesc o caracteristica data. Procedurile de verificare a ipotezelor sunt asemanatoare celor utilizate pentru variabile calitative.

Alegerea testului potrivit se va face in functie de numarul esantioanelor, volumul acestora si modul in care au fost selectate.

Schema decizionala din figura nr. 4.1 are rolul de a intruma in alegerea testului corespunzator.

4.1 Testul "z" pentru compararea proportiei din esantion cu cea din populatie

In unele ocazii se pune problema testarii proportiei w obtinute pe baza datelor din esantion cu valoarea proportiei din populatie, reala sau cu o valoare teoretica p. De exemplu, in urma unui sondaj realizat intr-o companie multinationala cu privire la atitudinea salariatilor fata de mutarea sediului companiei, ponderea obtinuta a persoanelor de sex feminin in esantion a fost de 35,6%. Stiind din surse administrative ca in realitate salariatele detin o pondere de 32% se pune problema compararii celor doua proportii.

Distributia teoretica corespunzatoare repartizarii proportiilor este distributia binomiala. Totusi, se considera ca distributia normala este o buna aproximatie a acesteia atunci cand sunt indeplinite conditiile: si . Daca esantioanele nu sunt de volum redus aceste conditii in practica sunt de cele mai multe ori satisfacute.

Figura nr. 4.1 Schema decizionala pentru testarea variabilelor calitative

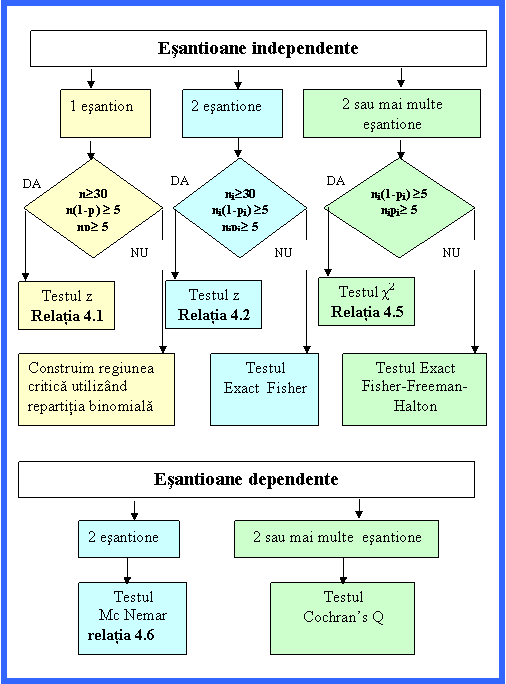
Cand utilizam distributia normala pentru a testa proportia din esantion, testul statistic este urmatorul:

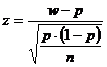(relatia 4.1)

unde w= proportia din esantion iar p = proportia din populatie.

a)      test bilateral

In aceasta forma a testului se determina doua limite si se utilizeaza in cazul in care caracteristica calitativa este dublu tolerata.

H₀: w= p si H₁:

Regiunea critica in cazul testului bilateral este:

W:

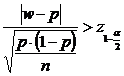
Daca valoarea calculata z_c luata in modul este inferioara valorii tabelate corespunzatoare nivelului de semnificatie putem considera ca nu exista diferente semnificative intre w si p si se accepta ipoteza nula.

b)     test unilateral stanga

H₀: w= p si H₁:

Regiunea critica pentru testul unilateral stanga este: W:

Daca valoarea calculata z_c este mai mica decat valoarea tabelata corespunzatoare nivelului de semnificatie se respinge ipoteza nula si se accepta ipoteza alternativa.

c)      test unilateral dreapta

H₀: w= p si H₁:

Regiunea critica este: W:

Daca valoarea calculata z_c este mai mare decat valoarea tabelata corespunzatoare nivelului de semnificatie se respinge ipoteza nula si se accepta ipoteza alternativa.

In cazul in care conditiile: si nu sunt indeplinite nu se va putea utiliza distributia normala, probabilitatile exacte trebuind preluate din tabela distributiei binomiale.

4.2. Compararea proportiilor provenite din doua esantioane independente

Compararea proportiilor obtinute pe baza prelucrarii datelor din doua esantioane independente este frecvent utilizata in prelucrarea si analiza statistica a rezultatelor sondajelor deoarece permit evidentierea existentei diferentelor semnificative intre regiuni de dezvoltare sau intre grupuri sociale. Totodata acestea permit si analiza variabilelor ce nu sunt masurate pe o scala parametrica.

Utilizarea acestui test presupune ca ambele esantioane sa fie de volum normal (n₁, n₂ ≥ 30). In plus n₁w₁, n₁(1-w₁), n₂w₂, n₂(1-w₂) trebuie sa fie ≥5. Aceste conditii sunt necesare pentru ca distributia normala utilizata sa fie o buna aproximatie a distributiei binomiale.

Pentru a intelege semnificatia acestor conditii consideram tabelul urmatorul tabel de contingenta:

Tabel nr. 4.1

Este necesar ca toate frecventele interioare ale tabelului de contingenta sa fie ≥5.

Deoarece ipoteza de egalitate a proportiilor implica si ipoteza egalitatii dispersiilor, testul statistic utilizat va fi similar celui pentru compararea a doua medii din doua esantioane independente cu s s₂ necunoscute.

Ipotezele testului bilateral sunt:

si

Statistica testului este: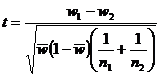 (relatia 4.2)

w₁= proportia observata in esantionul 1; n₁= volumul esantionului 1;

w₂= proportia observata in esantionul 2; n₂= volumul esantionului 2;

= variatia estimata pe baza proportiilor selectiilor dupa relatia: .

In functie de modul de definire a regiunii critice si acest test se poate efectua ca test bilateral, unilateral dreapta sau unilateral stanga. Valoarea calculata a testului se compara cu valoarea corespunzatoare nivelului de semnificatie ales si numarului de grade de libertate df=n₁+n₂-2.

In cazul in care conditiile privind marimea esantioanelor si a frecventelor interioare ale tabelului de contingenta nu sunt respectate rezultatele testului Student nu prezinta incredere.

In aceasta situatia vom substitui testul Student cu Testul Exact Fisher. A fost descris de Fisher in lucrarea sa "The Design of Experiments" in 1935.

Consideram un tabel de contingenta de forma celui prezentat in tabelul 4.1. Ne asumam frecventele marginale ca fiind fixe si distribuim frecventele interioare construid toate tabele posibile.

Tabel nr. 4.2

Astfel, pornid de la tabelul de contingenta 4.2, in conditiile pastraarii frecventelor marginale fixe toate tabelele posibile sunt:

Tabel nr. 4.3

Pentru fiecare tabel probabilitatea de aparitie este calculata pe baza relatiei:

(relatia 4.3)

Tabel nr. 4.4

Particularitatea testului este ca nu presupune calcularea unei statistici. Prin insumarea probabilitatilor ce corespunt tabelului de referinta (a=3) si a celor din extrema puternica (a=4 si a=5) se obtine nivelul de semnificatie al testului . Acesrta se compara cu a=0,05. Daca este mai mic se considera ca exista diferente semnificative intre proportiile celor care indeplinesc caracteristica. In cazul de fata p=0,634615385, mult mai mare decat a=0,05 ceea ce va duce la acceptarea diferentei nule intre proportii.

Dupa cum se poate observa aplicarea acestuia este greoaie. Deoarece testul exact este insa util in cazul esantioanelor de volum redus el poate fi efectuat sub toate softurile statistice moderne.

De exemplu in SPSS acesta se calculeaza automat pentru tabele de contingenta de forma 2X2 in cazul in care exista cel putin o frecventa interioara mai mica decat 5 sau daca marimea totata a esantionului este mai mica de 20 unitati observate.

4.3. Compararea proportiilor provenite din doua sau mai multe esantioane independente

Compararea proportiilor estimate pe baza a doua sau mai multe esentioane independente se realizeaza cu ajutorul testului χ² (Pearson's Chi-Squared test).

Acesta reprezinta practic o extensie a testului Student utilizat pentru compararea a doua proportii (relatia 4.2).

Prezentarea datelor se va face tot sub forma unui tabel de contingenta dar care de data asta poate avea mai multe coloane (pentru ca acem mai mult de 2 grupuri) si mai multe linii (caracteristica poate lua mai multe valori).

Tabel nr. 4.5

In tabelul 4.5 este prezentat un un tabel de contingenta de foema 2xk. Se pune problema sa comparam proportiile celor care indeplinesc caracteristica pentru toate cele k esantioane.

Notam cu 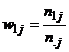proportia celor care indeplinesc caracteristica in esantionul (grupul) j. Aceasta reprezinta estimatorul proportiei celor care indeplinesc caracteristica in populatia j din care a fost selectat esantionul j notata cu .

Ipotezele testului sunt:

si .

Testul statistic χ² a fost construit pentru a patratul diferentelor dintre frecventele observate n_ij si cele asteptate e_ij . Frecventele asteptate se calculeaza plecand de la premiza: daca esantionul (grupul) nu are influenta asupra caracteristicii analizate atunci proportia celor care poseda caracteristica in grupul j este este aceeasi cu proportia celor care poseda caracteristica in total. Relatia de cacul a frecventelor asteptate este:

(relatia 4.4)

Unde i=1,..,l (numarul de linii - care in cazul de fata este 2) iar j=1,..,k (numarul de coloane - reprezinta numarul eesantioane (grupuri) pentru care se compara proportiile).

Statistica testului este:

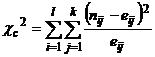(relatia 4.5)

Valoarea calculata se compara cu valoarea cu valoarea teoretica coresunzatoate nivelului de semnificatie ales si numarului de grade de lipertate calculat dupa relatia df=(l-1)*(k-1). In situatia in care se respinge ipoteza egalitatii proportilor.

Compararea proportiilor provenite din doua esantioane dependente

Principalul avantaj al utilizarii panelurilor il reprezinta posibilitatea analizei longitudinale. In cazul in care variabila este cantitativa, modificarile intervenite pot fi evidentiate prin testul Student pentru observatii perechi prezentat anterior. Pentru testarea diferentei procentelor se utilizeaza testul Mc Nemar.

"Am comite o grava eroare daca am aplica formulele esantioanelor independente. Aici trebuie cunoscut pentru fiecare individ statutul sau in cele doua anchete pe care il putem rezuma pe baza tabelului de contingenta 2x2 al efectivelor din cele doua anchete." Tabelul de contingenta are urmatoarea forma:

Tabel nr. 4.6

Aplicarea testului Testul Mc Nemar porneste de la ipotezele:

H₀= p_.1= p_1. si H₁= p_.1≠ p₁

Deoarece volumul esantioanelor din cele doua anchete este acelasi ipotezele se reduc la:

H₀= n_.1= n_1.    H₁= n_.1≠ n_1.

Cum n_.1= n₁₁+ n₂₁ iar n_1.= n₁₁+ n₁₂ H₀ se reduce la a testa n₁₂=n₂₁

Se va utiliza testul χ² frecventa teoretica fiind (n₁₂+n₂₁)/2.

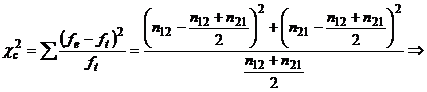
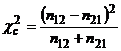(relatia 4.6)

Comparam rezultatul obtinut cu valoarea teoretica a lui χ² pentru un nivel de semnificatie dorit si numarul de grade de libertate corespunzator ((l-1)*(c-1)). Daca χ²_c>χ²_t se respinge ipoteza nula si se accepta ipoteza alternativa.

In situatia in care numarul esantioanelor dependente pentru care dorim sa verificam ipoteza egalitatii proportiilor este mai mare de 2 recurgem la testul Q al lui Cochran, considerat o extensie a testului Mc Nemar.

Teste statistice utilizate pentru verificarea ipotezelor privind proportiile sub SPSS

In situatia in care dorim sa comparam proportia in esantion a celor care poseda o caracteristica cu proportia in populatie cunoscuta din surse administrative alegem testul binomial urmand calea: Analyze/ Nonparametric Test/ Binomial. Dupa selectarea testului se deschide fereastra din figura nr. 4.2.

Baza de date utilizata este obtinuta in urma unui sondaj realizat in randul salariatilor unei companii din sectorul energetic.Pentru a testa reprezentativitatea esantionului vom compara proportia angajatilor de sex masculin din esantion cu cea calculata de cei de la departamentul de resurse umane.

Din lista variabileleor existente in baza de date se selecteaza variabila (sau variabilele) pentru care dorim sa efectuam testul.

In situatia in care variabila selectata este dihotomica (o variabila calitativa masurata pe scala nominala care are doar doua trepte) obtinerea grupurilor in vederea calcularii proportiei este realizata dupa modul de definire al variabilei in baza de date. In cazul in care variabila testata poate lua mai multe valori este necesar sa setam punctul care imparte esantionul formand doua grupuri.

Figura nr. 4.2 Fereastra de definire a testului binomial

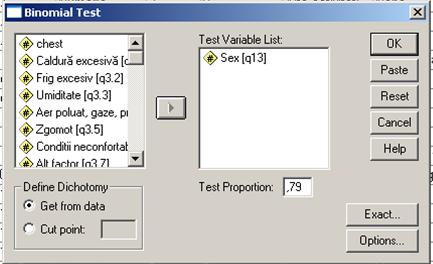
In campul Test Proportion introducem valoarea cunoscuta a proportiei din surse administative.

Odata definit testul se comanda efectuarea acestuia prin butonul OK. In urma procesarii se obtine outputul din tabelul nr. 4.6.

Pentru cele doua grupuri sunt afisate: numarul de observatii, proportia fiecarui grup in esantion si proportia teoretica (cea preluata din surse administrative).

Tabel nr. 4.6

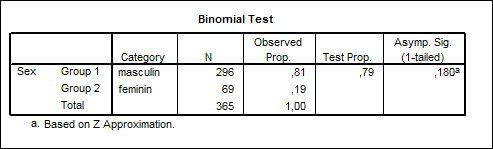
Daca valoarea afisata in coloana Asymp. Sig. este mai mica decat 0,05 se respinge ipoteza egalitatii proportiilor cu o probabilitate de (1-Asymp. Sig.).

In exemplul considerat putem spune ca nu exista diferente semnificative intre proportia din esantion si cea din populatie nu exista diferente semnificative statistic.

In SPSS nu avem posibilitatea sa procesam testul Student pentru testarea ipotezelor cu privire la doua proportii (calculate ca pondere a celor care detin o caracteristiica in doua esantionane independente). In acest caz vom apela la testul χ² (acesta poate fi utilizat pentru compararea proportiilor din doua sau mai multe esantioane independente). Pentru aceasta este necesar sa construin tabelul de contingenta urmand calea: Analyze/ Descriptive Statistics/ Crosstabs.

Figura nr. 4.3 Fereastra de definire a testului χ²

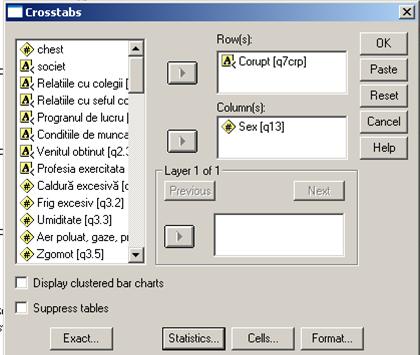
Din lista de variabile cuprinse in baza de date se selecteaza in fereastra Row(s) variabila pentru care dorim sa testam egalitatea proportiilor. In fereastra Column(s) vom trece variabila ce constituie criteriul de delimitare a grupurilor. Pe baza acestor informatii se va construi tabelul de contingenta de forma 2x2.

Am selectat variabila "Sex" drept criteriu de departajare a grupurilor. Dorim sa aflam daca exista diferente semnificative intre cele doua grupuri in ceea ce priveste proportia celor care considera seful direct ca fiind corupt.

Pentru ca statistica testului χ² sa fie procesata este necesar sa intram in submeniul Statistics de unde selectam aceasta optiune.

Daca dorim ca in outputul returnat sa avem pe langa frecventele observate (n_ij din tabelul teoretic 4.5) si alte informatii, deschidem mediul Cells iar fereastra care se deschide este prezentata in figura nr. 4.4.

Figura nr. 4.4 Selectarea optiunilor pentru tabelul de contingenta..

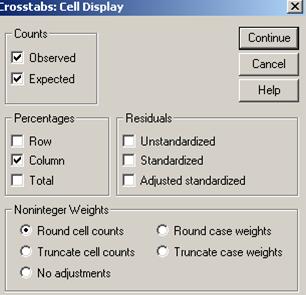
Deoarece dorim calcularea proportiilor celor care poseda caracteristica (au dat raspunsul da la intrebarea "Este seful direct corupt?") pentru fiecare grup am selectat optiunea Precentage Column.

Ca urmare a bifarii optiunii Counts Expected se vor afisa si frecventele asteprate (e_ij). Rezultatele procesarii testului sunt prezentate in tabelul 4.7 (tabelul de contingenta) si 4.8 (rezultatul aplicarii testului χ²).

Seful direct este apreciat ca fiind corupt de catre 14,5% dintre respondentii de sex masculin si de 15,9% in cazul sexului feminin.

Ipotezele testului bilateral sunt: si

Tabel nr. 4.7

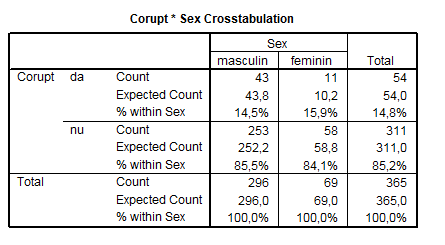
Valoarea calculata a testului =0,089. In cazul unui tabel de contingenta 2x2 numarul de grade de libertate calculat ca df=(l-1)*(k-1)=1. Valoarea teoretica ce corespunde acestor grade de libertate si unui nivel de semnificatie de a=0,05 este 3,84. Deoarece valoarea calculata este mai mica decat cea teoretica se accepta ipoteza diferentei nule.

In tabelul testului este afisata valoarea p=0,766 in cazul testului bilateral. Reprezinta valoarea riscului cu care am accepta ipoteza alternativa. Deoarece in general ne asumam un risc de doar 5% este necesar ca valoarea p sa fie mai mica de 0,05.

Tabel nr. 4.8

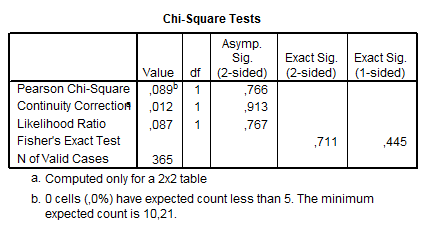
Deoarece testul χ² reprezinta o procedura adecvata pentru esantioane mari este necesar ca, in cazul esantioanelor de volum redus sa analizam cu mai multa atentie outputurile procesate.

Tabel nr. 4.9

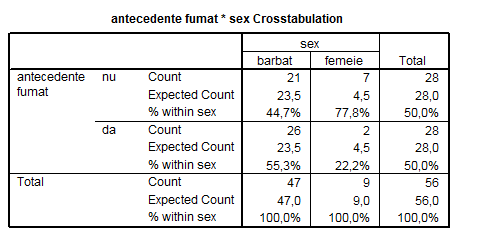
S-a realizat un studiu pe un grup de 56 de persoane inregistrate cu probleme cardio-vasculare. Pornind de la variabila "Sex" si variabila "Antecedente fumat" s-a obtinut tabelul de contingenta 4.9. Dintre pacientii de sex masculin au fumat 55,3% iar dintre pacientii de sex feminin 22,2%. Pentru a vedea daca exista diferente semnificative statistic intre cele doua proportii utilizam si de data aceasta testul χ². Rezultatele procesarii acestuia sunt prezentate in tabelul 4.10.

Tabel nr. 4.10

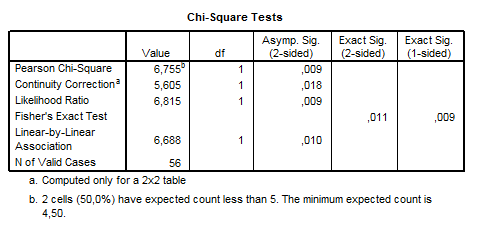
Deoarece exista frecvente asteptate mai mici de 5 (vezi tabelul 4.9) valoarea calculata a testului χ² nu mai are stabilitate. Din acest motiv in decizia de acceptare / respingere a ipotezelor este necesar sa analizam valorile p calculate pentru testul exact al lui Fisher. Testul efectuat este bilateral. In aceste conditi, pentru o valoare p=0,011 (mai mica decat 0,05) se respinge ipoteza diferentei nule si se accepta alternativa . Probabilitatea cu care putem afirma ca exista diferente semnificative in proportia de pacienti fumatori barbati respectiv femei este de 0,989 (calculata ca 1-0,011).

In cazul in care dorim sa comparam proportiile din mai mult de 2 esantioane vom utiliza tot testul χ². S-a realizat un sondaj in randul salariatilor unei societati comerciale. Pornind de la variabilele "Studii" si "In general apreciati pozitiv relatiile cu colegii?" s-a construit tabelul de contingenta 4.11. Cei cu studii primare apreaciaza pozitiv relatiile in proportie de 63,6%, cei cu studii medii 96,3% iar cei cu studii superioare 87,5%. Exista diferebte semnificative intre aceste proportii?

Tabel nr. 4.11

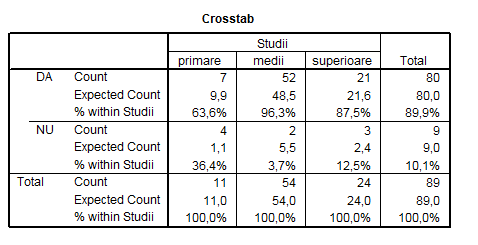
Ipotezele testului sunt:

si .

Rezultatele procesarii testului sunt prezebntate in tabelul 4.12. Deoarece exista 2 celule cu frecvente asteptate mai mici decat 5 este necesar ca din fereastra de definire a testului (vezi figura nr. 4.3) sa intram in submeniul Exact pentru a selecta efectuarea testului exaact al lui Fisher.

Valoarea p=0,005 (mai mica decat 0,005)duce la respingerea ipotezei nule i acceptarea alternativei. Garantam cu o probabilitate de 99,5% ca proportiile celor care apreciaza pozitiv relatiilew cu colegii difera pe sexe.

Tabel nr. 4.12

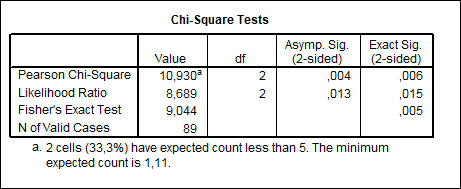
Pentru a arata modul in care putem utiliza procedurile SPSS-ului in verificarea ipotezelor statistice privind proportiile din esantioane dependente, am luat drept exemplu un studiu realizat pe un panel de 50 de pacienti inregistrati cu probleme cardio-vasculare. S-a urmarit variabila "prezenta simtomelor de agina pectorala". Pacienti au urmat tratament si dupa 6 luni au venit la control. Se pune problema sa verificam daca proportia celor care prezinta simptome de angina pectorala s-a modificat in urma tratamentului.

Fiind vorba de 2 esantioane dependente vom utiliza testul Mc Nemar. Obtinerea acestuia se poate face sub doua forme:

• Analyze/ Descriptive Statistics/ Crosstabs/ Statistics

Din submeniul Statistics se selecteaza testul Mc Nemar. In aceasta varianta putem obtine si un tabel de contingenta in care reprezentate frecventele observate in cifre obsolute si relative

• Analyze/ Nonparametric Tests / 2 Related Samples.

Alegand prima varianta am obtinut tabelul de contingenta 4.13. In primul val prezentau simptome de angina 62% din pacienti. In al doilea val procentul acestora s-a redus la 32%.

Ipotezele la care se reduce testul sunt:

H₀: n₁₂=n₂₁ H₁:_. n₁₂≠n₂₁

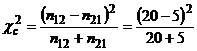=9

Tabel nr. 4.13

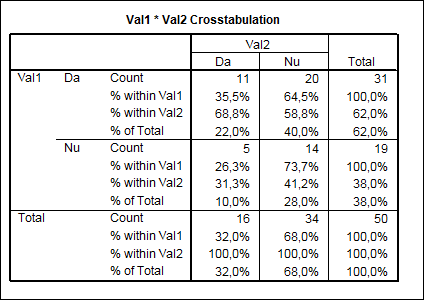
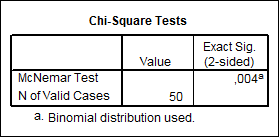
Valoarea p=0,004 (tabel nr. 4.14) este mai mica decat a=0,05. In aceste conditii se respinge ipoteza diferentei nule. Proportia celor care prezinta simptome de angina s-a ameliorat in urma aplicarii tratamentului.

Tabel nr. 4.14

Aplicatii ale testelor statistice utilizate pentru verificarea ipotezelor privind proportiile

Aplicatia 1

In randul agentilor economici din judetul Buzau s-a realizat un sondaj pe un esantion de 200 firme. 44% din firmele respondente sunt infiintate in ultimul an. Din surse administrative se stie ca acest procent este de 34%. Exista diferente semnificative statistic intre ponderea firmelor infiintate in ultimul an din populatie si estimatorul acesteia?

Rezolvare

N=200;     w=0,44; p=0,34

s

H₀: w= p si H₁:

Statistica testului este: 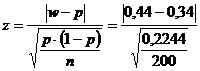=2,98

=1,96 pentru un nivel de semnificatie a=0,05 corespunzator unei probabilitati de garantare a rezultatelor de 95%.

Deoarece valoarea calculata este mai mare decat cea teoretica se respinge ipoteza diferentei nule

Aplicatia 2

In randul studentilor se realizeaza un studiu privind atitudinea tinerilor fata de fumat. Din cele 250 fete intervievate 32 % au declarat ca fumeaza iar din cei 190 baieti fumeaza 36%. Exista diferente semnificative statistic intre cele doua procente? Consideram nivelul de semnificatie a

Rezolvare

W₁= 0,32; n₁=250; w₂= 0,36; n₂=190

Ipotezele testului bilateral sunt: H₀: p₁=p₂ si p₁≠p₂

=0,337

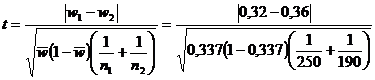=0,87

Valoarea teoretica a testului pentru un nivel de semnificatie a=0,05 si numarul de grade de libertate df=438 este 1,96. Valoarea calculata luata in valoare absoluta este mai mica, deci, se accepta ipoteza diferentei nule intre cele doua proportii

Aplicatia 3

In urma a doua anchete succesive realizate pe baza unui panel de 1600 persoane s-a constat ca 27% din cei intervievati in primul val au declarat ca traiesc mai bine decat anul trecut fata 30% care au optat pentru acest raspuns din valul al doilea. Sa se precizeze daca modificarea procentelor este semnificativa statistic pentru un nivel de semnificatie α=0,05. Tabelul de contingenta 4.15 este obtinut pe baza datelor din cele doua anchete.

Tabel nr. 4.15

Rezolvare

Se va utiliza testul χ² frecventa teoretica fiind (n₁₂+n₂₁)/2.

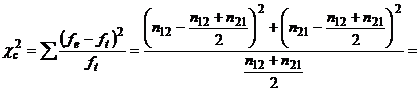
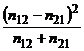
Comparam rezultatul obtinut cu valoarea teoretica a lui χ² pentru un nivel de semnificatie α=0,05 si numarul de grade de libertate df=1. . Deoarece χ²_c>χ²_t se respinge ipoteza nula si se accepta ipoteza alternativa, ceea ce denota ca s-a produs o modificare reala a gradului de multumire fata de nivelului de trai actual raportat la perioada precedenta.

Aplicatia 4

In randul studentilor unei universitati s-a realizat un sondaj stratificat pe ani de studiu. Ponderea studentilor care lucreaza este 26,67% pentru anul I, 41,67% din anul II si 54,55% din anul III. In urma prelucrarii datelor s-a obtinut tabelul de contingenta 4.16.

Tabel nr. 4.16

Sa se verifice daca exista diferente semnificative statistic pe ani de studiu intre proportiile celor care lucreaza.Rezultatele se vor gasranta cu o probabilitate de 95%.

Rezolvare

Pentru a compara proportiile celor care lucreaza din cele trei esantioane independente vom utiliza testul statistic χ2.

Ipotezele acestuia sunt:

si .

Statistica testului este: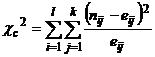

Calculam frecventele asteptate (prezentate in tabelul 4.17) conform relatiei: .

Unde i=1,..,l (numarul de linii - care in cazul de fata este 2) iar j=1,..,3 (numarul de coloane - reprezinta numarul esantioane pentru care se compara proportiile).

Tabel nr. 4.17

=20,998

Valoarea calculata se compara cu valoarea teoretica coresunzatoate nivelului de semnificatie a=0,05 si numarului de grade de lipertate calculat dupa relatia df=(l-1)*(k-1)=(2-1)*(3-1)=2. =5,9

Deoarece se respinge ipoteza egalitatii proportilor.