Sa se studieze giroorizontul cu corectie de tip proportional montat pe o platforma fixa fata de Pamant

Tema de proiect

Sa se studieze giroorizontul cu corectie de tip proportional montat pe o platforma fixa fata de Pamant,atingand urmatoarele puncte:

- trasarea caracteristicilor , , , cu si fara frecare,neglijand sau nu si ;

- se vor considera cazurile = si pentru fiecare din situatiile de mai sus

Valori numerice : , , , , , .

I. Chestiuni teoretice

Pentru determinarea vizuala a pozitiei aeronavei in raport cu planul orizontal local, se folosesc echipamente numite giroorizonturi, iar pentru formarea unor semnale electrice proportionale cu unghiurilr de ruliu si de tangaj, se utilizeaza giroverticalurile.

Echipamentele giroscopice de verticala au in componenta giroscoape astatic rapide in suspensie cardanica exterioara (GAR). Suspensia cardanica este formata din doua cadre de suspensie, axa de rotatie proprie (directia vectorului ) coincizand cu verticala locului.

Formarea indicatiilor cu privire la unghiurile de ruliu si de tangaj se realieaza cu ajutorul unei machete a aeronavei si a unei linii de referinta, numita linia orizontului.

Ecuatiile de miscare ale giroorizontului

Schema cinematica a echipamentului giroscopic este prezentata in figura 1. Sistemele de coordonate utilizate sunt - triedrul orizontal legat de traiectoria de zbor, avand axa - tangenta al traiectorie, - axa verticala, - axa perpendiculara pe cele doua anterioare; oxyz - triedrul RESAL legat de cadrul interior al suspensiei cardanice.

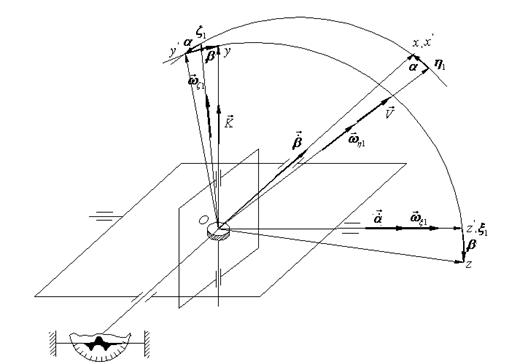
Fig. 1

Daca giroscopul este neperturbat (), triedrul oxyz se suprapune peste . Giroorizontul perturbat trece din pozitia in pozitia ox^'y^'z^' (rotatie cu unghiul in jurul lui ) si din pozitia ox^'y^'z^' in pozitia oxyz (rotatie cu unghiul in jurul axei cadrului interior ox); - vitezele unghiulare absolute in jurul axelor triedrului .

(1)

Utilizand forma vectoriala a ecuatiilor de precesie (; - momentul rezultant ce creeaza ), se obtin, pentru axele ox si, respectiv, oy, ecuatiile

(2)

Expresiile vitezelor unghiulare _x si _z vor fi urmatoarele

(3)

Neglijand momentele exterioare si de amortizare din axele celor doua cadre de suspensie, momentele M_x , M_z au expresiile

(4)

unde si sunt momentele de corectie din axele ox si oz, iar - momentele de frecare uscata din axele ox si oz (M_fx si M_fz - valorile acestor momente).

Inlocuind relatiile (3) si (4) in relatiile (2) scrise scalar (K _z=-M_x , K _x=M_z) si impartind ecuatiile la K se obtin

(5)

unde _fz=M_fx/K si _fx=M_fz/K sunt vitezele unghiulare "de frecare" (datorate momentelor de frecare uscata din axele cadrelor suspensiei cardanice).

Giroorizont montat pe o platforma fixa fata de Pamant

Platforma fiinf fixa fata de Pamant (V = = 0), rezulta a, si implicit, (verticala aparenta se suprapune peste verticala reala).

Ca urmare, neglijand termenii ecuatiile :

devin

clear all;close all;

omega=(4.167/1000)*(pi/180);omegafx=0.15*(pi/180);omegafz=0.2*(pi/180);

fi=40*(pi/180);psi=30*(pi/180);V=7000/36;g=9.81;R=64*(10^5);

omegacsi1=-omega*(cos(fi))*(sin(psi));

omegazita1=omega*(sin(fi))+V/(R*cos(fi));

omegaita1=omega*(cos(fi))*(cos(psi));

epsilon1=4.5/(0.5*60);epsilon2=3/(0.5*60);

hi1=0;hi2=0;

sim('schema2');

t=1:length(alfa);

h=figure;plot(t,alfa);title('alfa(t)');xlabel('timp[s]');ylabel('alfa[rad]');grid;

h=figure;plot(t,beta);title('beta[t]');xlabel('timp[s]');ylabel('beta(rad)');grid;

h=figure;plot(alfa,beta);title('alfa(beta)');xlabel('alfa[rad]');ylabel('beta[rad]');grid

Figura1

Figura2

Figura3

Figura4

Figura5

Figura6

Figura7

Figura8