APLICATII - JOCURI STRATEGICE SI OPTIMIZAREA DECIZIILOR

APLICATII - JOCURI STRATEGICE SI OPTIMIZAREA DECIZIILOR

Probleme rezolvate

Aplicatia 1. Sa se determine solutia Wald, Neumann si Harcwitz pentru o matrice a platilor date de egalitatea:

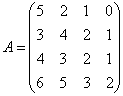
Rezolvare. a) Solutia Wald (pesimista) consta in determinarea acelei perechi i₀ si j₀ pentru care .

Vom fixa pe rand indicele "i" si vom calcula pentru fiecare caz , dupa care vom calcula indicele "i₀" care realizeaza maximul acestor minime.

Solutia se determina imediat daca se calculeaza pentru fiecare linie un numar si se selecteaza cel mai mare din aceste numere.

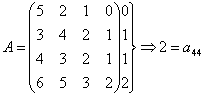
b) Solutia Neumann consta in determinarea acelei perechi (i₀,j₀) pentru care avem .

Fixam pe rand pe "j" si calculam maximele, dupa care vom determina cel mai mic dintre aceste maxime.

Se constata ca are loc egalitatea urmatoare:

a = 2 = a₄₄. Prin urmare perechea (i₀,j₀) = (4,4) este punct de echilibru.

c) Solutia optimista (Harcwitz)

Se presupune ca gradul de optimism cu privire la alegerea celei mai avantajoase solutii este p = 0,8. Vom determina perechea (i₀,j₀) pentru care are loc egalitatea:

.

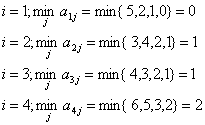
Aplicatia 2. Se da matricea de forma urmatoare:

a)      Sa se verifice daca exista punct de echilibru in strategii simple;

b)      Sa se gaseasca punctul de echilibru in strategii mixte.

Rezolvare. a) In strategii simple exista punct de echilibru daca are loc relatia urmatoare: V₁=V₂.

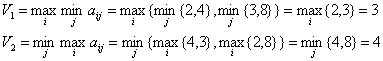
Se observa ca V₁<V₂ deci nu exista punct de echilibru.

b) In strategiile mixte trebuie determinata perechea pentru care au loc relatiile urmatoare:

cu respectiv cu .

.

Aplicatia 3. Doi fermieri supun unor jucatori o controversa relativa la o fasie de pamant lata de 6 m, care separa proprietatile lor.

Ambii revendica proprietatea intregii fasii.

Ei stiu ca jucatorul va cere fiecarei parti sa avanseze o propunere pentru a stinge controversa si apoi sa accepte propunerea. Daca ambii accepta propunerea in aceeasi masura sau nu accepta nimic, judecatorul va imparti fasia la jumatate.

Sa se determine cele mai bune propuneri ale fermierilor, limitand propunerile la cantitati intregi.

Rezolvare. Cei doi fermieri pot face fiecare urmatoarele propuneri (in cantitati intregi): - fiecare primeste intreaga fasie si - nu primeste nimic. Atunci matricea castigurilor din punct de vedere al primului jucator va fi:

Cum ==1/2, jocul este cu punct sa, strategiile optime ale celor doi fermieri fiind , respectiv , caz in care fiecare va primi jumatate din fasie.

Aplicatia 4. Un angrosist de instalatii de aer conditionat se obliga ca pana la 1 aprilie sa achizitioneze un numar de instalatii pentru a le revinde si instala in timpul stagiunii estivale. Bazandu-se pe cererea anului precedent, el estimeaza ca, cu probabilitatea 0,1, va vinde numai 5 unitati, cu probabilitatea 0,3 va vinde 10 unitati, cu probabilitatea 0,4 va vinde 15 unitati si cu probabilitatea 0,2 va vinde 20 unitati. Unitatile de aer conditionat pot fi comandate numai in grupe de cinci, costul unitar fiind 1000 dolari si pretul de revindere 1300 dolari (cu cheltuielile de instalare). Toate unitatile nevandute pana la sfarsitul sezonului se restituie constructorului in schimbul a 800 dolari, incluzand cheltuielile de transport.

Sa se stabileasca numarul optim de instalatii pe care sa le achizitioneze angrosistul.

Rezolvare. In tabelul 1 este data matricea jocului ( a platilor). Astfel, se calculeaza din enuntul problemei, ca se castiga 300 dolari pentru fiecare unitate vanduta si se pierd 200 dolari pentru fiecare unitate nevanduta. De exemplu, daca se comanda 15 unitati si nu se vand decat 10, atunci se castiga 3 000 dolari pentru 10 unitati vandute, din care se scad 1 000 dolari pentru cele 5 unitati ramase in stoc, obtinandu-se 2 000 dolari castig, care reprezinta elementul din linia , coloana . Deci avem:

Tabelul 1

Daca in stabilirea deciziei optime a angrosistului se tine seama numai de consecintele economice, atunci se pot aplica criteriile maximin, maximax si minimax.

a) Prin criteriul maximinim se stabileste cea mai mare valoare minima din toate actele de decizie. Utilizarea acestui criteriu conduce la o strategie foarte prevenitoare (precauta) pentru ca se va avea in vedere tot ce este mai rau posibil sa se intample.

Din punct de vedere al calculului, se alege minimul fiecarei coloane si dintre acestea se gaseste maximul :

Conform acestui criteriu, cea mai buna decizie pe care trebuie sa o ia angrosistul este , ea conducandu-l la cea mai mica pierdere pe care ar putea-o suporta.

b) Criteriul maximax este cel conform caruia cel mai bun act posibil este cel cu valoarea maxima cea mai mare din toate actele de decizie (varianta a criteriului lui Hurwicz). El se bazeaza pe un principiu fundamental opus criteriului maximin si anume pe principiul optimist al celui mai bun lucru care se poate intampla.

Se calculeaza maximul fiecarei coloane si dintre aceste elemente se alege maximul:

Deci, decizia optima a angrosistului din punctul de vedere cel mai optim este , adica sa comande 20 unitati de aer conditionat.

c) Analiza efectuata prin intermediul criteriul minmax se bazeaza pe prudenta.

Se alege, astfel, din maximul fiecarei coloane, cel mai mic element

Cea mai prudenta decizie a angrosistului este deci .

d) Acelasi criteriu minimax poate fi utilizat pe o alta matrice a jocului, ale carei elemente se numesc pierderi conditionate ale oportunitatii (regrete) si reprezinta pentru fiecare strategie diferenta dintre castigul economic al acelei strategii si castigul economic cel mai bun in cazul in care se verifiva un anumit eveniment, sau, in cazul in care natura este intr-o stare data (criteriul lui Savage).

De exemplu, sa presupunem ca are loc evenimentul , atunci strategia cea mai buna a angrosistului este , castigul sau economic fiind 1 500 dolari (maximul elementelor din prima linie). Deci pierderile conditionate de acest eveniment se obtin scazand din castigul cel mai bun fiecare castig corespunzator fiecarei strategii a angrosistului.

Matricea pierderilor conditionate ale oportunitatii va fi asadar:

Tabelul 2

Pierderea maxima a oportunitatii determinata de fiecare decizie se gaseste in ultima linie a tabelului 2. Minimul lor este 2 000 dolari, care va stabili ca este strategia optima a angrosistului dupa criteriul minimax aplicat matricei regretelor.

Aplicatia 4. Jocul investitiilor

Consideram a fi o corporatie cu doua sucursale si un sediu central. Fiecare sucursala raporteaza centralei veniturile estimate a fi obtinute in urma implementarii unui proiect comun (b₁). Costurile asociate realizarii proiectului sunt de 100 de unitati monetare. Proiectul va fi acceptat daca veniturile pe care le va aduce depasesc costurile, respectiv daca b₁ + b₂≥ 100. Daca proiectul este acceptat, atunci fiecare sucursala va trebui sa trimita centralei veniturile estimate initial si va primi de la centrala o suma fixa A_i precum si costurile aferente. Daca proiectul nu este acceptat, atunci castigurile sucursalelor vor fi nule. Stiind ca. A₁ este de cel putin 20 de unitati monetare, se cere:

a)      scrieti functia de castig pentru sucursala 1 in raport cu b₁ si b₂.

b)      determinati strategiile dominate pentru sucursala I. Exista strategii dominante pentru aceasta sucursala?

Rezolvare:

a)  Functia de castig

Pentru sucursala 1 avem:

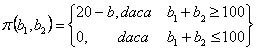
b)  Strategii dominate

Evident, b₁ < 20 domina b₁≤ 20. Fiecare valoare b₁ este cea mai buna pentru sucursala 1, daca proiectul este acceptat.

Strategiile nedominate ale diviziunii 1 sunt . Prima sucursala nu are o strategie dominanta, cea mai buna alegere a lui b₁depinzand de alegerea lui b₂.

Aplicatia 6. Jocul controlului

Aceasta situatie se poate aplica in diverse situatii, cum ar fi: inspectia armelor (pentru ca soldatii sa pastreze armele curate), prevenirea crimelor, controalele financiare sau in supravegherea muncitorilor si motivarea lor la o anumita activitate.

Vom descrie jocul astfel: un muncitor (jucatorul 1) lucreaza pentru un patron (jucatorul 2). Muncitorul poate fie sa munceasca (M) fie sa chiuleasca (C), acestea fiind, singurele strategii avute la dispozitie. Patronul poate fie sa vina in inspectie (I) fie sa nu vina (NI). In cazul in care vine in inspectie, poate avea o mai buna evidenta a modului in care muncitorii sai lucreaza, dar acest lucru ar fi costisitor, adica l-ar costa h.

Patronul va plati un salariu w muncitorului, mai putin in cazul in care il va prinde chiulind, cand ii va taia ziua de munca si muncitorul va primi atunci 0. (Nu il va putea obliga sa plateasca amenda, dar il poate sanctiona neplatindu-i ziua de munca). Pentru muncitor, "costul' unei zile de munca este c, iar, in cazul in care munceste, produce pentru patron valoarea v. Pentru simplificare, sa presupunem ca c > h > 0 si ca w > c (altfel nu ar mai avea sens sa munceasca).

Se cere:

a)      sa se descrie jocul sub forma normala prin intermediul matricei castigurilor;

b)      sa se determine echilibrul jocului si sa se comenteze rezultatul;

c)      sa se determine contractul optimal oferit de patron.

Rezolvare:

a) Forma normala

Jocul sub forma normala este prezentat in figura 1:

P

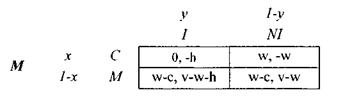
Figura 1.

b) Determinarea echilibrului

Observam usor ca acest joc nu are un echilibru in strategii pure (daca patronul nu va face inspectie, atunci muncitorul va prefera sa chiuleasca; daca patronul decide sa inspecteze, iar muncitorul afla acest lucrul, atunci ar fi mai bine sa munceasca. Patronul, in schimb, stiind ca muncitorul ar prefera sa munceasca, este mai castigat daca nu face inspectia). In acest caz, patronul trebuie sa aleaga o strategie mixta.

Fie x probabilitatea ca muncitorul sa chiuleasca si y probabilitatea ca patronul sa inspecteze. In figura 1. a fost reprezentata situatia. Muncitorului ii este indiferent daca munceste sau chiuleste, in cazul in care:

y*0 + (1-y)*w = y*(w-c) + (1-y)*(w-c) adica y*w = c (*)

Ii este indiferent daca alege intre a chiuli si a munci, atat timp cat valoarea castigului din a chiuli (c) este egala cu pierderea de venit y * w.

Patronului ii este indiferent daca alege intre a inspecta si a nu inspecta, atat timp cat:

x * (-h) + (l - x)(v - w - h) = x * (- w) + (l - x) * (v - w) adica

h x*w = h => (**)

Pentru patron, fiindu-i indiferent daca inspecteaza sau a nu, costul inspectiei h trebuie sa fie egal cu salariul economisit la plata muncitorului x * w.

Deci, singurul echilibru al jocului considerat ar fi un echilibru in strategii mixte descris prin relatia: .

d)      Contractul optimal

Plecand de la acest rezultat, se poate calcula si contractul optimal ce este oferit de patron, adica salariul w ce va maximiza castigul atasat al patronului:

(l - x)v - (l - xy)w - hy.

Din rezolvarea acestei probleme rezulta simplu ca Pentru un w dat (w > c), patronul poate alege , cu arbitrar de mic si, in acest caz, muncitorul va munci cu probabilitatea 1, iar castigul (aproximativ) pentru patron va fi:.

Aplicatia7. Jocul falimentului

In cadrul acestui joc vom presupune ca jucatorii sunt un bancher si efectiv un grup de lucratori. Bancherul poate acorda un credit lucratorilor sau poate refuza acordarea acelui credit. Daca bancherul crediteaza si lucratorii muncesc, intreprinderea poate produce un venit care depinde de starea naturii. Exista trei stari ale naturii: cea mai prielnica este cea "normala' (1), cu o probabilitate de 0,9, iar celelalte doua stari sunt "rea' (2) si foarte "rea' (3), respectiv falimentul si inchiderea - cu probabilitate de 0,05 fiecare. Probabilitatile productiei sunt prezentate in figura 2.:

Figura 2.

Costul de oportunitate al capitalului este de 0,01 si creditorul, fiind orientat spre profit, ofera un imprumut de 1000 pentru a permite desfasurarea productiei. Rata dobanzii este de 10%, deci trebuie returnat 1100 la sfarsitul perioadei.

Presupunem, de asemenea, ca lucratorii mai pot avea o alternativa de a castiga din alta afacere 1500. Daca imprumutul este facut, starea naturii este cunoscuta si participantii isi reconsidera strategia conform noilor informatii.

Se cere:

a)             analizati derularea jocului si stabiliti daca banca acorda imprumutul prin inductie recursiva;

b)            care este nivelul imprumutului care poate fi acordat de banca pentru a
nu pierde si lucratorii sa accepte creditul?

Rezolvare:

Ce se poate intampla in starea 3? Membrii cooperativei demisioneaza, in sensul ca se a considera cele mai bune oportunitati alternative, 1500 > 1000 deci cooperativa la care sunt lucratorii inceteaza sa mai existe si creditorul nu mai primeste nimic.

Dar in starea I? Veniturile intreprinderii sunt suficiente ca sa poata fi platita datoria de 1100 si salariile de 1900, salarii care sunt mai mari decat cele mai bune alternative, deci salariatii vor ramane si vor produce, iar ambii jucatori, banca si cooperativa lucratorilor, au cele mai bune rezultate.

In starea 2, venitul este suficient de mare ca datoriile sa fie platite, dar lucratorii primesc doar 900, numar care este mai mic decat 1500. In acest caz, membrii lucratori ai cooperativei vor demisiona si cooperativa se va dizolva din lipsa de membri, iar banca nu va primi nimic. Pe de alta parte, daca banca va renegocia plata partiala a 500 sau mai putin, atunci lucratorii vor primi 1500 si afacerea continua.

Deci, in aceasta stare, banca renegociaza si castiga 500. Valoarea asteptata de banca este: 0,9 (1100) + 0,05 (500) + 0,05 (0) = 1015 > 1010.

Deci banca castiga mai mult decat cea mai buna alternativa si accepta contractul. Pentru lucratorii din cooperativa se obtine urmatoarea valoare asteptata:

0,9 (1900)+ 0,05 (1500)+ 0,05 (1500)= 1860 > 1500

Si ei, de asemenea, accepta contractul. Astfel imprumutul este facut, in ciuda unei probabilitati de faliment de 0,05.

In multe jocuri de acest fel, unul sau altul dintre jucatori poate obtine un rezultat mai bun daca el insusi se implica credibil din start intr-o strategie care poate parea mai putin avantajoasa, imediat ce starea naturii este cunoscuta si ceilalti au luat deja deciziile. Va avea banca un rezultat mai bun daca se angajeaza ea insasi sa negocieze? Raspunsul este ca nu.

Castigul ei va fi: 0,9 (1100) + 0,05 (0) + 0,05 (0) = 990 < 1010.

Creditorul va avea rezultate mai slabe daca, de exemplu legislatia interzice renegocierea sau ei pot refuza sa mai faca imprumutul.

Vom analiza alte doua situatii distincte ce privesc situatia muncitorilor. Prima dintre acestea este starea de "sclavie', respectiv situatia in care muncitorii nu pot parasi firma (dintr-un motiv sau altul, cum ar fi lipsa altor locuri de munca sau contracte dificile). In acest caz, ar fi dorinta muncitorilor ca intreprinderea sa fie abandonata daca datoria este platita in starea 2. Dar daca ei ar fi legati in vreun fel de firma? "Sclavia' ofera o posibilitate. Intr-un sistem care permite "sclavia', "antreprenorul' cumpara sclavi in loc sa inchirieze lucratori liberi. In starea naturala 3 antreprenorul inchiriaza sclavi ca forta de munca pentru 1500, platind datoria de 1100 si incasand profit (asigurand costul hranei necesare pentru a mentine sclavii productivi mai putin de 400). In starea 2 antreprenorul va solicita sclavi care sa lucreze pentru firma, produce 2000, plateste datoria si castiga 900 unitati monetare, mai putin hrana sclavilor. Banca isi va primi datoria in oricare stare si va prefera poate sa-l crediteze (sa-1 imprumute) mai curand pe stapanul sclavilor decat pe acea cooperativa a lucratorilor.

Al treilea caz il reprezinta cel al "inchirierii' muncitorilor pe baza unei alegeri mutuale, dar, in acest caz, patronul se asteapta ca lucratorii sa-i plece oricand altcineva le va oferi mai mult.

In acest exemplu, imprumutul este facut asociatiei cooperatiste de lucratori. Daca ar fi fost facuta indivizilor, ei ar fi fost mai putin responsabili fata de imprumut dupa ce s-ar fi mutat la slujbe mai bine platite. Dar obligatia de a plati imprumutul a fost asumata de grupul de lucratori, luati ca grup, si grupul nu poate exista decat atata vreme cat este in interesul lucratorilor sa existe. Aceasta nu reflecta constituirea firmei, ci constituirea liberala a societatii care sustine ca nici o agentie, chiar si cea constituita de lucratori, nu poate cere unei persoane sa lucreze fara a-i oferi un salariu cu care acesta sa fi fost de acord initial.

Proprietarii sau corporatia investitoare este mai mult decat un mijlocitor intre grupul de lucratori si banca, in ceea ce priveste falimentul.

In concluzie, esenta falimentului consta in renegocierea contractului de imprumut intre un creditor si un grup de lucratori, dar si in legile care scutesc creditorul de suma datorata in unele conditii. Aceste legi protejeaza creditorii si nu debitorii.

Aplicatia 8.Jocul intrarii pe piata

Se considera un joc in care jucatorii sunt doua firme, din care una este deja pe piata, iar a doua doreste sa intre. Prima firma poate sa se extinda construind o noua fabrica, cea de-a doua nu cunoaste costul acestei noi constructii, stie doar ca poate fi de 4 unitati sau 1 unitate.

Castigurile sunt descrise in figura 3.1 a) si b), prima varianta:

Castigurile jocului pot fi, de asemenea, urmatoarele (varianta a doua):

Se cere:

a)           sa se determine echilibrul jocului in informatie incompleta pentru situatia descrisa in figura 3.1;

b)          determinati echilibrul pentru jocul in informatie incompleta descris in figura 3.2;

c)           analizati echilibrul prin abordarea Harsanyi.

Rezolvare:

a) Cazul 3.1

Castigurile celui de-al doilea depinde doar de faptul ca primul a construit (sau inca nu) o noua fabrica, nefiind influentat de costul acestei investitii si ar fi preferabil sa intre pe piata doar daca jucatorul 1 n-ar construi fabrica.

Pentru jucatorul 1, in schimb, vedem ca strategia de a construi este dominanta doar daca ar avea un cost mic.

Notam cu p₁ probabilitatea cu care jucatorul 2 crede ca jucatorul 1 suporta un cost mare. Cum 1 construieste doar daca ar avea un cost mic, atunci 2 va intra pe piata pentru probabilitatea p₁ > 1/2 si nu va intra cu probabilitatea p₁ < 1/2.

b) Cazul 3.2

Notam cu y probabilitatea ca jucatorul 2 sa intre pe piata (deci (1 - y) este probabilitatea ca 2 sa nu intre pe piata).

In acest caz, strategia de a nu construi fabrica ramane dominanta, daca jucatorul 1 suporta un cost mare.

Daca este vorba de un cost mic, atunci strategia optima a lui 1 depinde de probabilitate ca 2 sa intre pe piata.

A construi este mai bine decat a nu construi daca:

1,5y +- 3,5 (1 -y) > 2y + 3 (1 -y). Rezulta y < 1/2 .

Astfel, 1 poate incerca sa prezica comportamentul lui 2 pentru a-si alege propria strategie.

Aplicatia 9.Negocierea salariului

Vom considera o firma ce doreste angajarea unei persoane intr-o anumita profesie. Presupunem ca firma cunoaste productivitatea marginala a persoanei care doreste sa se angajeze, in timp ce solicitantul locului de munca stie salariul sau de oportunitate.

Notam:

p_a - pretul cerut de cel ce doreste sa se angajeze;

p₁ - pretul oferit de firma;

v_a - valoarea fortei de munca in conceptia celui ce doreste sa se angajeze;

v_f - valoarea aceleiasi forte de munca in conceptia firmei ce doreste sa se angajeze.

Negocierea are loc dupa relatia:

- daca p_f ≥ p_a atunci are loc angajarea, salariul de angajare fiind:

- daca p_f < p_a cel ce doreste sa fie angajat este refuzat.

Consideram ca v_a si v_f sunt variabile aleatoare independente, uniform distribuite in intervalul [0,1] si reprezinta informatia privata pentru fiecare dintre cele doua parti participante la negociere.

Definim functiile de castig la nivelul fiecarui jucator astfel:

persoana care isi ofera serviciile:

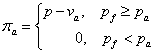
pentru firma:

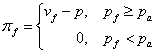
Vom nota:

- strategie la nivelul persoanei ce doreste sa se angajeze (pretul cerut de ele pentru fiecare v_a);

- o strategie la nivelul firmei (pretul oferit de firma pentru fiecare valoare).

Se cere sa se determine echilibrul Bayesian al jocului.

Rezolvare:

Perechea de strategii (,) este un echilibru Bayesian (EB) daca sunt indeplinite urmatoarele conditii:

Oricare ar fi [0,1], rezolva problema de optim:

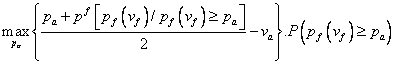(1)

unde: reprezinta pretul anticipat de firma, conditionat de pretul cerut de cel ce isi ofera serviciile, probabilitatea corespunzatoare.

Oricare ar fi [0,1], rezolva problema de optim:

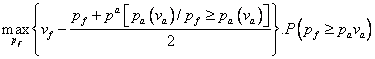(2)

unde: reprezinta pretul anticipat de cel ce isi ofera serviciile, conditionat de pretul oferit de firma.

Vom descrie in continuare unul dintre echilibrele existente pentru acest joc:

presupunem ca = , de unde se deduce ca pretul p_a este uniform distribuit in intervalul ;

presupunem ca =, deci p_f este uniform distribuit in intervalul .

Ca urmare, relatiile (1) si (2) devin:

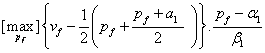
Conditiile necesare de optim conduc la:

de unde: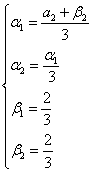

si corespunzator:

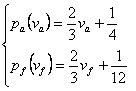
Graficul corespunzator este redat in figura 4:

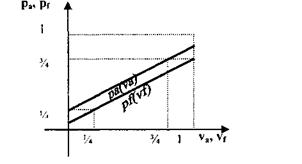
Figura 4.

Consideram variabila aleatoare v, cu v [0,l] respectand strategia firmei de a oferi pretul v atunci cand valoarea fortei de munca (celui ce doreste sa se angajeze) in viziunea firmei este mai mare sau egala cu v si 0 in rest.

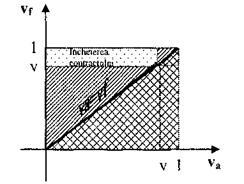
Reprezentarea grafica este ilustrata in figura 5.

Deci firma va accepta sa-1 angajeze pe cel ce isi ofera serviciile numai atat timp cat v_fv.

Multimea strategiilor pentru firma este:

in timp ce, pentru cel care doreste un loc de munca, ar fi:

Discutie:

daca accepta salariul v, atunci contractul intre cele doua parti se incheie, putandu-se considera cel mai bun raspuns al celui ce doreste sa se angajeze si, in consecinta, un echilibru Bayesian.

daca salariul v este refuzat, atunci negocierile pot continua, orice valoare

v < fiind o solutie pentru firma si, odata acceptata, reprezinta cel mai bun raspuns pentru cel ce-si ofera serviciile.

In figura precedenta zona punctata este aceea a perechilor pentru care contractul se incheie si reprezinta puncte de echilibru Bayesian.

Probleme propuse

1. Se da un joc J pentru care se cunoaste matricea platilor

Sa se verifice daca exista punct echilibru in strategii multiple.

2. Intr-un magazin se pot vinde 2,3,4, sau 5 televizoare in timp de 3 luni, cu probabilitatile 0,3; 0,4; 0,2 si 0,1, respectiv. Bazandu-se pe aceste probabilitati, cate televizoare sunt necesare in stoc, presupunand ca nu se pot face alte comenzi in timpul celor 3 luni?

3. Un comerciant achizitioneaza un anumit produs platind 3 dolari bucata si il revinde cu 5 dolari bucata, produsul fiind perisabil si de nefolosit dupa 5 zile. Pe baza experientei anterioare comerciantul stie ca cererea produsului este un numar intre 9 si 12 bucati inclusiv.

Sa se determine matricea castigurilor si sa se stabileasca actiunea cea mai buna a comerciantului prin:

a)      criteriul maxim;

b)      criteriul maximax;

c)      criteriul Savage.

In conditiile problemei precedente, comerciantul estimeaza ca probabilitatile de bucati cuprinse intre 9 si 12 sunt respectiv 0,3; 0,4; 0,2 si 0,1. Care este actiunea sa cea mai buna prin criteriul Bayes?