Controlul de receptie al produselor

Controlul de receptie al produselor

I. Nivelul de calitate acceptabil (AQL) si planurile de control statistic de receptie

I.1 Controlul prin esantionare si riscurile furnizor/beneficiar

-Concepte si definitii

-Stabilirea riscului producatorului.

-Stabilirea riscului beneficiarului

-Stabilirea simultana a riscurilor a furnizorului si beneficiarului

I.2. Caracteristica operativa a planurilor de control statistic

I. 3. Volumul produselor controlate in procesul receptiei loturilor

I. 4. Nivelul de calitate acceptabil

I1. Controlul prin esantionare si riscurile furnizor/beneficiar

I.1.1Concepte si definitii

Pentru ca o economie sa functioneze este necesar ca intre partenerii economici sa se realizeze un schimb de resurse de: materii prime, materiale, energetice, produse, servicii si lucrari. Schimburile intre diversii parteneri economici, cel mai adesea se fac sub forma de loturi, lotul fiind constituit pe principiul omogenitatii unitatilor constituente, metodele de receptie fiind adaptate acestui gen de livrari.

Verificarea calitatii produselor din lot se poate efectua printr-un control 100% (integral) si partial.

Controlul calitatii loturilor poate fi efectuat printr-o gama variata de metode adaptate la specificul productiei controlate, tipului caracteristicilor de calitate, importantei si implicatiilor erorilor de decizie.

Astfel deosebim dupa natura caracteristicilor controlate:

-controlul atributiv, care are ca scop sa stabileasca daca caracteristicile se incadreaza sau nu la nivelul prescriptiilor, produsele fiind apreciate in functie de acest criteriu in "corespunzatoare" sau "necorespunzatoare";

-controlul prin masurare, are ca obiectiv stabilirea valorii numerice a caracteristicilor calitative produselor, incadrarea lor in limitele de toleranta prevazute.

Dupa volumul produselor controlate deosebim:

-control 100%;

-control prin esantionare.

Fiecare dintre grupele de metode enumerate prezinta avantaje si deficiente.

Pentru controlul loturilor de produse cu volum mare se utilizeaza controlul prin esantionare.

Sinteza elementelor necesare efectuarii esantionarii pentru receptia loturilor se regaseste sub forma planului de control, care contine: riscurile asumate de partenerii controlului (furnizor, beneficiar), nivelul calitatii productiei si criteriile de decizie.

Pentru conditiile cele mai generale se recomanda sa se utilizeze prevederile din standarde, iar pentru cazurile care nu se incadreaza in prevederile din standarde se pot construi planuri adecvate.

Clauzele referitoare la calitatea productiei, la planul de control utilizat, se inscriu in contractele economice, unde se prevad si alternative pentru respingerea loturilor controlate.

Controlul prin esantionare reprezinta o forma particulara a testarii ipotezelor statistice. Prin aplicarea unui plan de control statistic trebuie sa se decida daca lotul de produse poate fi sau nu acceptat.

Pornind de la ipoteza ca orice lot contine o anumita portie de produse necorespunzatoare, denumita fractiune defectiva a lotului P₁ care teoretic poate lua valori intre 01. Scopul controlului de receptie este de a stabili daca aceasta fractiune defectiva depaseste sau nu un anumit nivel critic P₀, stabilit in functie de considerente de ordin economic. In acest caz se intalnesc doua situatii:

-H₁:P£P₀ -lot acceptabil si

-H₂:P>P₀ -lot respins.

Esenta controlului statistic de receptie consta in aceea ca aprecierea calitatii lotului de marime N se face pe baza unui esantion de marime n (n<<N), extras intamplator din lot, sau mai precis pe baza unui parametru de esantionare (media, abaterea medie patratica, frecventa defectiva). Se stie ca parametrii esantionului nu coincid cu cei ai intregului lot, ci se abat intamplator de la acestia. Din cauza acestor abateri, parametrii lotului se estimeaza numai cu o anumita probabilitate. In consecinta, orice decizie cu privire la lot (acceptarea sau respingere) comporta un anumit risc de a fi eronata.

Controlul statistic de receptie poate conduce la doua feluri de decizii eronate:

-respingerea unui lot care contine o fractiune defectiva P mai mica decat fractiunea defectiva admisa P₀ si care ar trebui deci acceptat, sau altfel spus respingerea ipotezei H₁:P£P₀, care in realitate este adevarata. Eroarea comisa in asemenea cazuri se numeste eroare de genul I. Probabilitatea comiterii erorii de genul I poarta numele de risc al furnizorului si se noteaza cu a

-acceptarea unui lot care contine o fractiune defectiva P mai mare decat nivelul fixa P₀. Eroarea astfel comisa se numeste eroare de genul II. Probabilitatea comiterii erorii de genul II este tocmai riscul beneficiarului de a accepta un lot care in realitate trebuie respins, si se noteaza cu b

Nici furnizorul si nici beneficiarul nu pot accepta riscuri prea mari, de aceea pentru reducerea acestor riscuri in primul caz se gaseste o valoare P₁ pentru care calificarea drept necorespunzatoare a lotului (respingerea) determina pierderi economice maxime, iar pentru situatia numarul doi se gaseste un P₂ pentru care decizia de acceptare a lotului determina pierderi economice maxime.

Valorile P₁ si P₂ impart intervalul de variatie a fractiunii defective P in trei domenii, (fig. 8.1):

-primul domeniu 0£P£P₁ -domeniul de acceptare;

-al doilea domeniu P₁ £P£P₂ -domeniul de indiferenta;

-al treilea domeniu P₂ £P£1 -domeniul de respingere.

Fractiunea defectiva P₁ pentru care probabilitatea de acceptare este foarte mare, cel putin 1-a, se numeste fractiunea defectiva acceptata, sau nivel de calitate acceptabil (AQL), deoarece loturile in acest caz se considera corespunzatoare calitativ.

Fractiunea defectiva P₂ se numeste fractiunea defectiva tolerata (LQ), deoarece in acest caz loturile se considera necorespunzatoare calitativ si beneficiarul le accepta cu o probabilitate foarte mica, cel mult b

Fractiunea P₀, corespunzatoare probabilitatii de acceptare P_a(P₀)=0,5, se numeste fractiunea defectiva probabila.

Marimile P1, P2, a si b in care se materializeaza cerintele care se pun controlului prin esantionare se stabilesc de catre furnizor si beneficiar de comun acord, tinand seama de considerente de ordin economic si de siguranta cu care se doreste sa se ia decizia. In consecinta, aceste marimi se stabilesc in mod diferentiat de la un produs la altul. Intre aceste marimi, in practica, exista urmatoarele relatii:

I.1.2. Stabilirea riscului producatorului

Pentru stabilirea riscului producatorului se face apel la repartitia hipergeometrica.

Fie un lot ce are un volum N de produse, ce se supune controlului, produsele controlate nu se reintroduc in lot, volumul esantionului este n, iar fractiunea defectiva a esantionului este P

Pentru stabilirea elementelor planurilor de control (riscuri, numar de acceptare si respingere) se va lua in considerare atat volumul intregului lot, cat si al esantionului ce se controleaza.

Notatii:

-Numarul produselor N (in lot) si n (in esantion);

-Numarul rebuturilor D (in lot) si d (in esantion);

-Numarul produselor corespunzatoare G (in lot) si g (in esantion);

-Fractiunea defectiva P (in lot) si p (in esantion);

-Proportia produselor necorespunzatoare Q (in lot) si q (in esantion).

Intre acesti indicatori exista urmatoarele relatii:

n=d+g; 1=p+q; =np; ; ;

N=D+G; 1=P+Q; ;; ;

Probabilitatea ca esantionul extras sa contina d rebuturi si g produse corespunzatoare se stabileste astfel:

Se stie ca   si

Rezulta ca :

Riscul furnizorului este determinat cu relatia:

a SP_(d)

unde

Aplicaie.

Avem de de verificat calitatea unui lot de produse finite, de volum N=100 unitati, controlul si decizia fiind luata pe baza verificarii unui esantion n=25 produse. Prevederile contractuale stabilesc ca lotul este corespunzator daca nivelul procentului de rebuturi este de cel mult 2%, deci sunt corespunzatoare loturile care contin D₁=NP₁=2 produse rebuturi.

Partile contractante au convenit asupra nivelului riscului a=0.05 de a respinge un lot corespunzator, astfel incat se poate stabili numarul admisibil de rebuturi in esantionul de volum n. Conditiile stabilite se incadreaza cel mai bine ipotezelor modelului hipergeometric, pe baza caruia vor fi efectuate si calculele.

In continuare se calculeaza probabilitatile cumulate ale repartitiei hipergeometricepana cand P(d£A)=0,95.Inlocuind datele problemei obtinem:

n=25; 1=p+q; =np; g=25-d,

N=100 ;

a SP_(d)=1-0,56+0,37+0,06=0,01

Rezulta ca a_calculat=0,01<a_stabilit

Pentru un asemenea esantion numarul produselor necorespunzatoare acceptabil este A=2, de unde numarul de respingeri este R=A+1=3. Daca In urma controlului numarul rebuturilor identificate este inferior sau cel mult egal cu 2, lotul se accepta, iar daca este egal sau superior lui 3, lotul se respinge

I.1.3. Stabilirea riscului beneficiarului

Se stabileste cu relatia:

b=P(d£A)

unde P(d£A)=P(d=0)+P(d=1)+.+P(d=A)

Aplicatie

Consideram ca avem de receptionat un lot de produse care sunt apreciate necorespunzator atunci cand procentul de produse necorespunzatoare este P₂=7%, restul conditiilor de receptie fiindN=100, n=20, A=2

b=P(d£2)=P(d=0)+P(d=1)+.+P(d=A)=0,198+0,375+0,285=0,858

b=P(d£2)=0,858, valoare foarte mare pentru beneficiar, comparativ cu cerintele initial formulate de catre acesta. Interesele beneficiarului sunt insuficient aparate printr-un asemenea plan de control care conduce la 85,8% acceptari de loturi cu P₂=7%. Plan de control neavantajos pentru furnizor, caci daca loturile au P₂=7%, beneficiarul va returna loturile necurespunzatoare acceptate initial. Aceste loturi vor fi integral controlate, produsele necorespunzatoare fiind inlocuite cu produse bune.

O asemenea situatie repetata frecvent este nefavorabila furnizorului. Calitatea productiei livrate de producator in conditiile prezentate este 0,07x0,858=0,06 sau 6% produse defecte

I.1.4. Stabilirea simultana a riscurilor a furnizorului si beneficiarului

Aplicatie

Fie urmatorul plan de control caracterizat prin: volumul lotului de control N=100 produse; esantionul n=20 unitati; P₁=0,04; numarul produselor necorespunzatoare acceptabil in volumul esantionului A=2. In aceste conditii se pune problema sa stabilim valorile riscurilor a si b

Avand in vedere restrictiile enumerate, se va utiliza modelul hipergeometric, rezultatele fiind prezentate in tabelul nr. 1. Deci un plan de control de tipul N=100, n=20, A=2, R=3 asigura nu mai mult de respingeri de loturi cu o calitate de cel mult  . Alegerea unui asemenea plan de receptie nu tine seama de eroarea de genul II, deci riscul beneficiarului (ciar daca implicit, riscul de genul II este prezent prin interdependenta dintre cele doua riscuri)

Tabelul nr. 1

Efectuanf calcule, in baza acelorasi ipoteze, rezulta o valoare acceptabila, cand N=100, n=20, A=2, R=3, P₂=.15%..(vezi tabelul 2

Tabelul nr. 2

I.2. Caracteristica operativa a planurilor de control statistic

Caracteristica operativa, reprezinta una din trasaturile definitorii, specifice, care deosebesc diferite planuri de control din punct de vedere al eficacitatii lor in separarea loturilor corespunzatoare de cele necorespunzatoare. Caracteristica operativa exprima intr-o forma matematica, specifica diferitelor planuri de control, probabilitatea acceptarii loturilor, in functie de marimea fractiunii defective.

Poate fi descrisa prin functia P_a=f(p), care exprima probabilitatea de acceptare a lotului ce contine o fractiune defectiva . Expresia grafica a caracteristicii operative o constituie curba caracteristicii operative (CO) ce are urmatoarea forma (fig. 8.2)

Curba caracteristica (fig. 8.2) ilustreaza faptul ca loturi de calitate acceptabila (P£P₀) pot fi totusi respinse, iar loturi necorespunzatoare (P>P₀) vor fi totusi acceptate.

Logic, in jurul valorii P₀ exista o zona de interferenta in care deciziile sunt echivalente, insa pe masura ce ne departam din P₀ spre zero, sau din P₀ spre 1, eroarea respingerii unui lot corespunzator si respectiv eroarea comisa prin acceptarea unui lot necorespunzator scade. Limitele acestei zone de interferenta se stabilesc in functie de considerente ecobnomice, de implicatiile luarii unor decizii false. Daca notam limitele cu P₁ fractiunea defectiva acceptata si P₂ fractiunea defectiva tolerata, putem stabili legatura dintre fractiunea defectiva si valorile riscurilor deciziei.

In fig. 8.3. se prezinta o curba operativa specifica controlului statistic si care permite evidentierea tuturor marimilor care definesc un plan de control prin sondaj. Se poate constata ca loturile corespunzatoare (P£P₁) sunt acceptate cu o probabilitate ridicata, apropiata de unitate, egala cu P=1-a, insa datorita erorilor de esantionare vor fi loturi respinse nejustificat intr-o proportie redusa, cu o probabilitate a. De asemenea loturi necorespunzatoare (P³P₂) sunt respinse cu o probabilitate ridicata P=1-b, dar sunt totusi acceptate, intr-o proportie redusa ssi cu o mica probabilitate egala cu riscul beneficiarului b. Cand calitatea lotului se afla intre P₁ si P₂ loturile sunt respinse cu o probabilitate 1-b a, probabilitate care descreste puternic pe masura ce ne indepartam din P₁   catre P₂ deci pe masura imbunatatirii calitatii.

I. 3. Volumul produselor controlate in procesul de receptie a loturilor.

Esantionul supus controlului este constituit din doua categorii de produse:

-produse care se incadreaza in valorile parametrilor de calitate stabiliti;

-produse care nu se incadreaza in valorile parametrilor de calitate stabiliti.

Numarul mediu de produse controlate la un lot, cand fractiunea defectiva este , se compune din:

-marimea esantionului n;

-numarul produselor controlate din cadrul loturilor respinse, acest numar este egal cu (N-n) inmultit cu P(d>A) al probei la care numarul

rebuturilor a fost mai mare ca A. Deci:

Factorul cu care se inmulteste (N-n) nu este a, probabilitatea respingerii loturilor cu fractiunea P₁, ci se stabileste prin repartitia binomiala sau Poisson. In cazul binomial P(d>A), cand P=P₁, rezulta din expresia:

I.3.1. Minimizarea volumului esantionului

Pentru intocmirea unui plan de control sunt utilizate tabelele din standardele de control, standarde alcatuite prin inventarierea celor mai uzuale conditii de receptie si calculul parametrilor planurilor de control prin efectuarea a diferitelor combinatii intre nivelurile marimilor de intrare. Deci cele mai cunoscute tabele enumerate sunt :

-standardele Dodge-Roming (1967) -DR, sunt intocmite numai pentru valori ale riscului beneficiarului, calitatea loturilor fiind apreciata in functie de fractiunea defectiva, nu sunt utilizate pentru receptia prin metode distructive;

-standardele americane din grupa MIL STD, cel mai utilizat fiind 105D pentru controlul prin atribute si 414 pentru controlul prin variabile (masurare). Aceste ultime standarde au cunoscut cea mai larga arie de raspandire, majoritatea standardelor nationale ale diferitelor tari fiind aliniate dupa prevederile acestora;

-in Romania sunt : STAS 3160-62; STAS 6658-62; STAS 6659-62; STAS 3160-72; STAS 8820-72; STAS 3160/1,2,3 din 1984, standarde prezentate in volumul II (Calitate si fiabilitate). Aceste standarde realizeaza o aliniere la standardele internationale si la recomandarile ISO.

I.3.2. Calitatea medie livrata

Existenta unei fractiuni de produse necorespunzatoare in fiecare lot si existenta posibilitatii luarii unei decizii false cu privire la calitatea productiei livrate, in continuare se va discuta despre urmatorii indicatori ce caracterizeaza aceste aspecte:

1. Calitatea medie dupa control (AOQ) -constituie un indicator al eficientei unui anumit plan de control si reprezinta calitatea medie a productiei livrate dupa controlul unui anumit numar de loturi.

In succesiunea operatiilor de control, alaturi de loturile acceptate vor fi loturi respinse, care se vor controla integral, iar produsele necorespunzatoare se vor substitui cu produse bune.

Daca esantionul, in cazul lotului acceptat, s-a reintrodus in lotul acceptat fara ca produsele necorespunzatoare sa fie substituite cu alte produse corespunzatoare, calitatea medie dupa control va fi:

AOQ=P P_a+O(1-P_a)=P P_a

Daca insa, esantionul este "filtrat" de produsele necorespunzatoare inainte de returnarea sa in lot dupa operatiunea de control, atunci indicatorul se stabileste cu relatia:

Atat beneficiarul cat si furnizorul au interesul de a cunoaste indicatorul AOQ, primul are interesul sa achizitioneze loturi cu o calitate medie dupa control, corespunzatoare fluxului sa de productie, al doilea are interesul sa aiba o calitate medie dupa control apropiata de calitatea loturilor prezentate de el la receptie.

2. Limita calitatii medii dupa control

Reprezinta valoarea maxima a indicatorului AOQ, fiind cel mai scazut nivel al calitatii medii acceptate, adica:

sau

Din relatia de calcul a calitatii medii dupa control, se poate realiza o aplicatie cu utilizari in analiza si interpretarea planurilor de receptie. Daca AOQL sunt cunoscute, atunci prin fixarea probabilitatilor de acceptare P_a(P₁)=1-a si P_a(P₂)=b se pot determina valorile P₁ si P₂ cu relatiile:

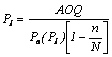si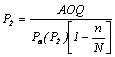

I.4. Nivelul de calitate acceptabil (AQL)

Reprezinta procentul maxim de produse defecte sau numarul maxim de defecte la suta de unitati de produs (Def./100up) pentru care lotul se considera acceptabil din punct de vedere al calitatii medii a productiei.

Valoarea AQL este fundamentala in aplicarea standardelor de control statistic al calitatii, furnizand in ultima instanta baza reala pentru acceptarea unui numar cat mai mare de loturi corespunzatoare si respingerea unui numar cat mai mare de loturi necorespunzatoare din punct de vedere calitativ.

Lucrarile de specialitate ca si standardele de control recomanda ca fixarea marimii AQL sa se faca la nivelul stabilit prin contractul incheiat intre parteneri.

In practica se observa ca beneficiarul, in mod nejustificat impune o anumita valoare AQL "universal valabila" pentru toate caracteristicile de calitate indiferent de gradul lor de importanta in aprecierea globala a calitatii produsului.

Furnizorul doreste pentru caracteristicile produselor care le livreaza un AQL cat mai mic, pentru a avea o protectie cat mai buna fata de calitatea produselor necorespunzatoare ce intra in firma sa.

In cazul cand produsele pot prezenta defecte de gravitati diferite, nivelul AQL se stabileste diferentiat pentru fiecare tip de defecte. O clasificare a defectelor le imparte in urmatoarele clase:

-defecte majore A -pun in pericol viata utilizatorilor;

-defecte majore B -cele care fac produsele nevandabile;

-defecte minore -cele referitoare la aspecte, care ar putea crea probleme de acceptare de catre beneficiar.

Dupa importanta caracteristicilor calitative se pot grupa in:

-critice; principale; secundare si minore, sau

-critice; majore; minore, sau

-critice 1; -critice 2; -majore 1; majore 2; minore 1; minore 2.

In aceste conditii in contractul de livrare se prevad atat valorile AQL diferentiate pe clase de defecte, cat si valori de acceptare diferite pentru fiecare fiecare tip de defecte.

In cazul cand exista un numar mare de caracteristici care se controleaza si pentru fiecare din ele se stabileste un AQL distinct (AQL₁, AQL₂, ., AQL_n) respectiv de defecte admisibile (A_1, A₂, ., A_n,) atunci nivelul global AQL_g se determina cu relatia:

, respectiv:

AQL reprezinta si in standardele pentru controlul calitatii unul din elementele invariante de identificare a unui plan de control. In situatia utilizarii STAS 3160/2-84, elementele planurilor de verificare sunt:

-nivelul de verificare obisnuit Nv=II si severitate normala (existand pentru situatii deosebite si niveluri speciale cu severitate ridicata) si niveluri speciale cu severitate ridicata;

-valorile AQL.

Clasele de gravitate corespund importantei relative a diferitelor defecte posibile ale produselor, grupare fiind efectuata astfel: critice, majore, iar caracteristicile speciale impun niveluri speciale de control simbolizate S₁-S₄.

Subclasele unui defect determina o verificare mai putin severa decat s-ar impune, iar supraclasarea conduce la alcatuirea unor scheme de control mai severe decat necesare.