Proiect la S.E.M

Universitatea Politehnica Timisoara

Facultatea de Management in Productie si Transporturi

Cuprins

Cap1. Prezentarea teoretica a sistemelor Fuzzy

1.1 Logica Fuzzy

1.2 Trasaturi specifice ale logicii Fuzzy

1.3 Variabile lingvistice

1.4 Sisteme Expert Fuzzy

1.5 Reprezentarea cunoasterii prin logica Fuzzy

Cap2. Aplicatie a inferentei Fuzzy

2.1 Fuzificarea valorii ferme

2.2 Analiza regulilor activate

3.3 Aplicarea inferentei Fuzzy

4.4 Defuzificarea

Cap3. Concluzii

1. Prezentarea teoretica a sistemelor Fuzzy

1.1 Logica Fuzzy

Logica fuzzy, introdusa de Dr. Lotfi Zadeh este un subset al logicii conventionale boolene, logica care a fost extinsa pentru a cuprinde conceptul adevarului partial valori ale adevarului cuprinse intre complet adevarat si complet fals .

Sistemele inteligente bazate pe logica bivalenta considera ca un obiect apartine unei multimi. Sistemele inteligente bazate pe logica fuzzy considera ca acel obiect poate apartine unei multimi, in grade diferite, generandu-se o flexibilitate a interpretarii situatilor.

Exista o stransa corelare intre logica fuzzy si conceptul de subset, in literatura de specialitate intalnindu-se cel mai des termenii de subset si set, care au aceeasi semnificatie in context cu cei de submultime respectiv multime.

Un subset U al setului S poate fi definit ca un set de perechi ordonate, cu cate un element apartinand setului S iar celalalt element inclus in setul , cu cate o pereche ordonata pentru fiecare element al lui S.

Aceasta regula stabileste corespondenta intre elementele setului S si setul . Valoarea 0 este utilizata pentru a reprezenta neapartenenta, iar valoarea 1 pentru a reprezenta apartenenta. Pentru a stabili daca propozitia x este in U este adevarata sau falsa, se cauta in perechile ordonate, astfel incat primul element al perechii sa fie x. Propozitia este adevarata daca cel de-al doilea element al perechii este 1, respectiv falsa daca acesta este 0.

In mod similar un subset fuzzy F al setului S poate fi definit ca un set de perechi ordonate, care au fiecare cate un prim element apartinand lui S, iar cel de-al doilea element este o valoare in intervalul [0,1]. Exista cate o pereche pentru fiecare element al lui S. Valoarea 0 este utilizata pentru a reprezenta neapartenenta, iar valoarea 1 pentru a reprezenta apartenenta totala, iar valorile intermediare sunt utilizate pentru a reprezenta grade de apartenente intermediare. In mod frecvent, apartenenta este descrisa de o functie functia de apartenenta a lui F. Gradul de adevar in propozitia x este in F se determina prin gasirea celui de-al doilea element al perechii ordonate al carui prim element este X.

1.2 Trasaturi specifice ale logicii Fuzzy

• In logica Fuzzy rationamentul exact este privit ca un caz limita al rationamentului aproximativ.

• In logica Fuzzy orice situatie este experimentata gradual.

• Orice sistem logic poate fi reprezentat in logica Fuzzy (fuzzyficare).

• In logica Fuzzy cunoasterea este interpretata ca o colectie de restrictii fuzzy elastice sau de echivalenta pe o colectie de variabile.

• Deductia este privita ca un proces de propagare al restrictiilor elastice.

• Multimea fuzzy are asociata o functie caracteristica care ia valori in intervalul [0,1], valorile acesteia descriind gradul de apartenenta al unui element la acea multime.

1.3 Variabile lingvistice

In logica Fuzzy domeniile corespund conceptelor de variabile lingvistice. Unei variabile lingvistice, iicorespunde un domeniu de valori posibile, care sunt definite pe un interval numit univers de discurs pentru variabila lingvistica respectiva. O problema care utilizeaza variabile lingvistice implica stabilirea multimii termenilor lingvistici asociati fiecarei variabile.

O variabila lingvistica este definita de un quintuplu format din: x, T(x), σ, U, M, unde:

• x este denumirea variabilei lingvistice;

• T(x) este multimea nevaga a denumirilor pentru valorile diferite ale variabilei lingvistice, adica un termen al variabilei lingvistice A;

• σ este operatorul sau cuantificatorul, care se aplica conform regulilor sinctactice si care genereaza termenii variabilei lingvistice;

• U este universul de discurs al aplicatiei;

• M este operator semantic, fiind utilizat pentru fiecare atasare a unei submultimi vagi din Universul de discurs, fiecarui termen T al variabilelor lingvistice.

1.4 Sisteme Expert Fuzzy

Sistemele expert fuzzy sunt SE care utilizeaza logica fuzzy in locul logicii traditionale (bivalente). Cu alte cuvinte, un SE fuzzy reprezinta o colectie de functii de apartenenta si reguli de rationament. Spre deosebire de SE traditionale, care sunt masini de rationament simbolic, SE fuzzy sunt orientate mai degraba spre procesare numerica. Regulile intr-un SE fuzzy sunt reprezentate intr-o forma asemanatoare cu:

DACA x este mai mic SI y este mai mare ATUNCI z=mediu

unde x si y variabile de intrare; z este variabila de iesire; mic - este o functie de apartenenta (subset fuzzy) definit pentru x; mare - este o functie de apartenenta definita pentru y, iar mediu - este o functie de apartenenta definita pentru z.

Partea din dreapta a lui ATUNCI se numeste concluzie sau consecinta. Majoritatea aplicatiilor care lucreaza cu logica fuzzy permit insa formularea mai multor concluzii pentru fiecare regula. Totalitatea regulilor este cunoscuta ca baza de reguli sau baza de cunostiinte.

Mecanismul prin care regulile si functiile de apartenenta sunt aplicate datelor de intrare si sunt calculate valorile de iesire, se numeste inferenta.

Sistemele expert fuzzy constau la randul lor in combinarea a patru subprocese: fuzificare, inferenta, compozitie, defuzificare.

• In procesul de fuzificare se aplica functiilor de apartenenta variabile de intrare, determinandu-se astfel gradul de adevar al fiecarei premise componente a regulilor. Un grad de adevar diferit de 0 va avea ca efect luarea in considerare a premiselor, deci regula va fi aplicata.

• In procesul de inferenta sunt calculate valorile de adevar ale premiselor, in functie de care vor fi activate regulile corespunzatoare acestora din baza de cunostinte. Concluziile regulilor activate le corespunde cate un subset fuzzy atasat iesirilor sistemului.

• Compozitia reprezinta procesul in care toate subseturile fuzzy corespunzatoare cate unei iesiri sunt combinate intre ele, rezultand un singur subset fuzzy pentru iesire.

• Procesul de defuzificare nu apare intotdeauna in aplicatii. El consta in transpunerea unui subset fuzzy intr-o singura valoare corespunzatoare unei iesiri.

1.5 Reprezentarea cunoasterii prin logica Fuzzy

Incercarile conventionale de reprezentare a cunoasterii prin retele semantice, cadre, calculul predicatelor si PROLOG se bazeaza pe logica bivalenta. Un impediment serios al acestor tehnici este inabilitatea de a reprezenta incertitudinea si imprecizia. Reprezentarea conventionala nu ofera un model adecvat pentru metodele de rationament, care sunt mai degraba aproximative decat exacte. Majoritatea metodelor rationamentului uman si toate metodele rationamentului comun se inscriu in aceasta categorie.

Logica Fuzzy, care poate fi privita ca o extensie a sistemelor logice clasice, ofera un cadru conceptual, care abordeaza problema reprezentarii cunoasterii, intr-un mediu al incertitudinii si impreciziei.

Esenta reprezentarii in logica Fuzzy se bazeaza pe semanticile test-scor, in cadrul carora o propozitie este interpretata ca un sistem de restrictii elastice,iar rationamentul este privit ca o propagare a restrictiilor elastice.

Cap2. Aplicatie a inferentei Fuzzy

Luarea deciziei de cumparare a aspiratorului este influentata decisiv de caracteristicile de baza ale acestui produs.

Finalitatea deciziei de cumparare implica un raport calitate-pret care sa satisfaca nevoile si dorintele clientilor.

Nivelul de acceptabilitate al aspiratorului tinand cont de acest raport este indicat luand in considerare urmatoarele variabile:

● consum

● fiabilitate

Universul de discurs , in acest caz, este urmatorul: dezvoltarea unui sistem expert suport pentru stabilirea pretului piesei de cunoastere.

2.1 Fuzificarea valorii ferme

Pentru indeplinirea acestui scop se folosesc urmatoarele elemente:

► de intrare: - consum

- fiabilitate

► de iesire: - pret

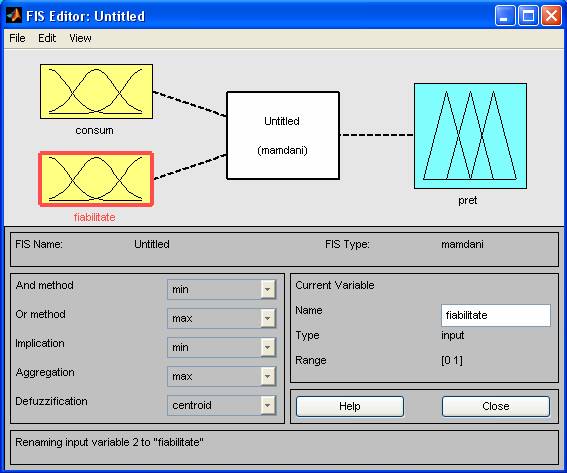
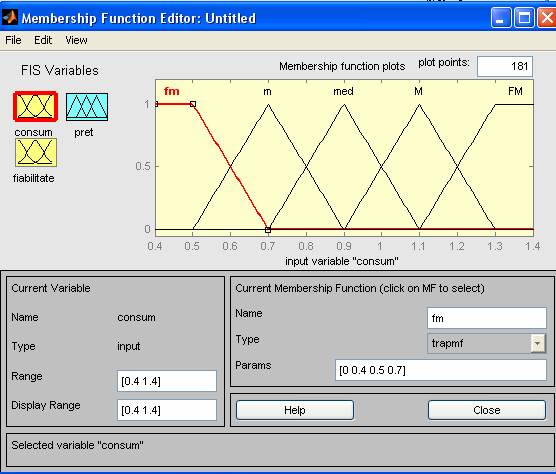
Pentru variabila de intrare consumul universul de discurs este cuprins in intervalul [0.4 1.4] (exprimat in kwh) si avand functiile de apartenenta :

fmic [0 0.4 0.5 0.7)

mic [0.5 0.7 0.9)

mediu [0.7 0.9 1.1 )

mare [0.9 1.1 1.3)

fmare [1.1 1.3 1.4 1.4]

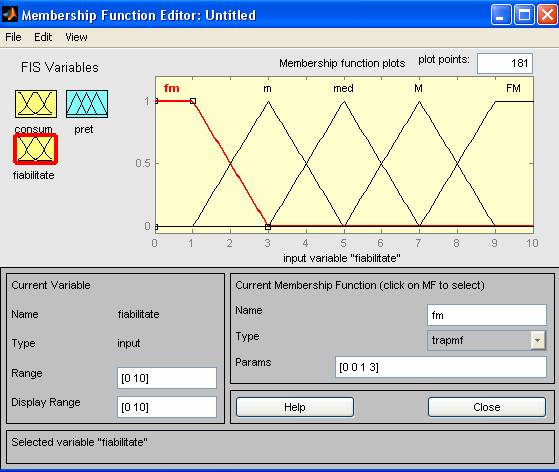
Pentru variabila de intrare fiabilitatea universul de discurs este cuprins in intervalul [0 10] si avand functiile de apartenenta :

fmic [0 0 1 3)

mic [1 3 5 )

mediu [3 5 7 )

mare [5 7 9)

fmare [7 9 10 10)

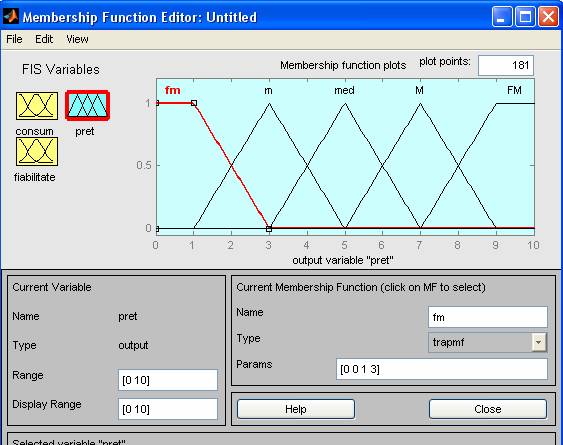
Pentru variabila de iesire pretul universul de discurs este cuprins in intervalul [o 10] si avand functiile de apartenenta:

fmic [0 0 1 3)

mic [1 3 5 )

mediu [3 5 7 )

mare [5 7 9)

fmare [7 9 10 10)

`2.2 Analiza regulilor activate

Plecand de la numarul de multimi fuzzy asociate fiecarei variabile de intrare va rezulta un numar de 55=25 reguli.

Acestea pot fi observate in captura de mai jos:

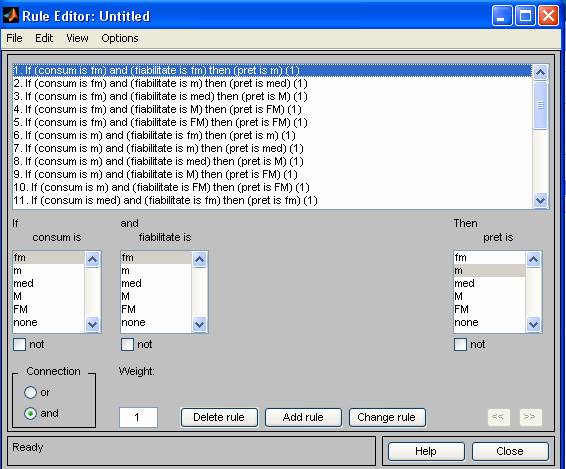
2.3 Aplicarea inferentei fuzzy

Pentru fiecare din regulile fuzzy stabilite in paragraful 2.2 se stabileste gradul de apartenenta al variabilei de iesire pret la multimea fuzzy respectiva, folosind operatorii combinati MAX(MIN).

2.4 Defuzificarea

Aceasta operatie consta in extragerea unei valori scalare, deterministe din informatia fuzzy, asociata variabilei de iesire sub forma multimii fuzzy.

Vizulaizarea regulilor reprezenatate sub forma grafica si a suprafetelor:

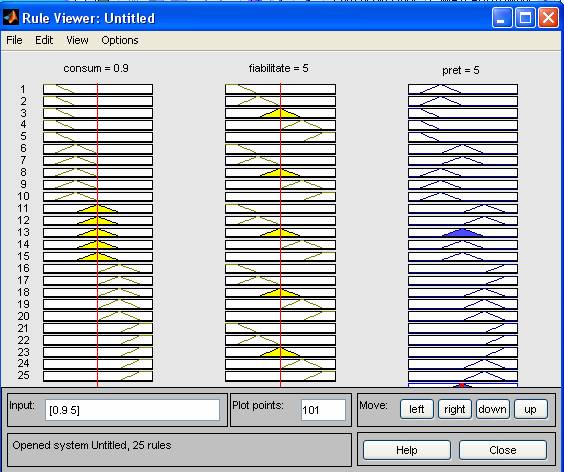
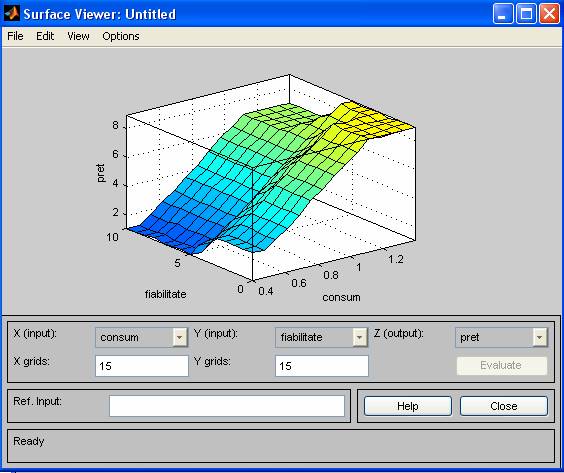
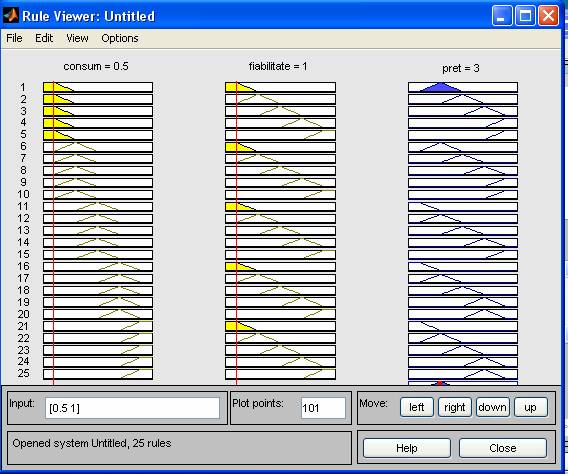
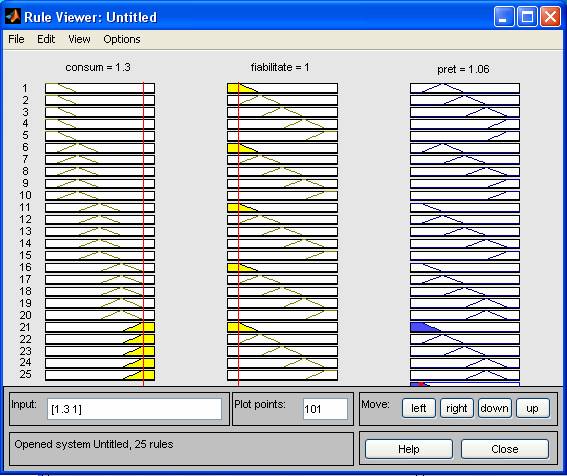
Exemplu 1:

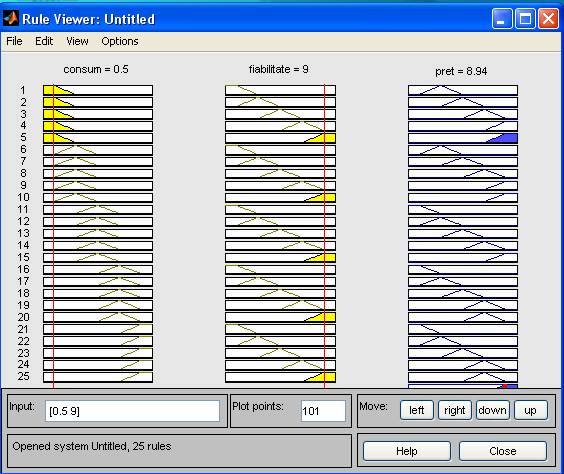
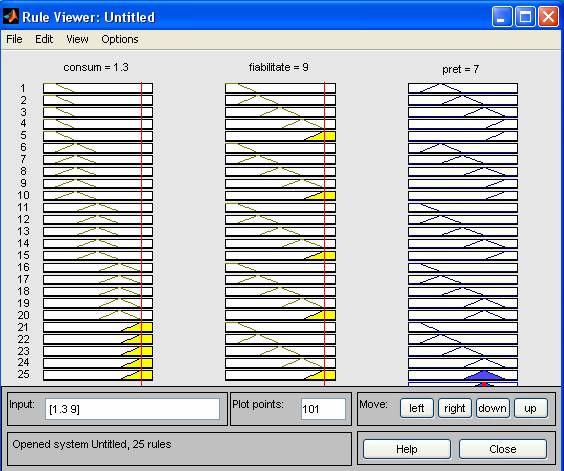
Exemplu 2:

Cap3. Concluzii

Se observa ca in exemplul 1 la un consum de 0.5 kwh si o fiabilitate notata cu 1(la o scara de la 0 la 10),pretul aspiratorului este de 3 (mil ROL),iar la aceeasi fiabilitate de 1 si la un consum mai mare -1.3kwh ,conduc la scaderea pretului aspiratorului-1.06.

Se observa ca in exemplu 2 la un consum de 0.5 kwh si la o fiabilitate notata cu 9,pretul este de 8.94(mil ROL).La aceeasi fiabilitate dar la un consum mai mare de energie -1.3,pretul aspiratorului este mai mic-7(mil ROL).

Din aceste 2 exemple rezulta ca pretul aspiratorului creste atunci cand are o fiabilitate mare si un consum mic de energie.