Scrigroup - Documente si articole

     

 
HomeDocumenteUploadResurseAlte limbi doc
 
AstronomieBiofizicaBiologieBotanicaCartiChimieCopii
Educatie civicaFabule ghicitoriFizicaGramaticaJocLiteratura romanaLogica
MatematicaPoeziiPsihologie psihiatrieSociologie


FUNCTIA MODUL

Matematica



+ Font mai mare | - Font mai mic



FUNCTIA MODUL.




PROPRIETATI.


FUNCTIA PARTE INTREAGA SI PARTE FRACTIONARA.


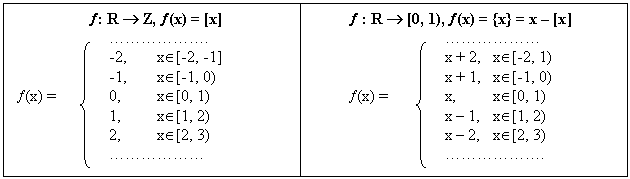
FUNCTIA EXPONENTIALA.

DEFINITIE. Fie a > 0, a Functia : R (x) = ax, se numeste functia exponentiala de baza a.
 


OBSERVATII. !. Baza a este diferita de 1 pentru ca in caz contrar (x) = 1x = 1 este considerata constanta si nu este considerata ca o functie exponentiala.

A nu se confunda functia exponentiala (x) = ax, a>0, a 1 cu functia g(x) = xa, xIR. Pentru prima functie a este baza puterii ax care este constanta, in timp ce pentru a doua functie a este exponentul puterii axa care este constant.

GRAFICUL FUNCTIEI EXPONENTIALE.

Graficul functiei exopnentiale se traseaza in doua cazuri:

Baza a I (0, 1) (spunem ca baza este subunitara). In acest caz graficul functiei este situat deasupra axei Ox si intersecteaza axa Oy in (0, 1). Graficul functiei exponentiale cu baza subunitara este din ce in ce mai apropiat de axele coordonate, cu cat baza este mai mica.

Baza a > 1 (spunem ca baza este supraunitara). In acest caz graficul functiei este situat deasupra axei Ox si intersecteaza axa Oy in (0, 1). Graficul functiei exponentiale cu baza subunitara este din ce in ce mai apropiat de axele coordonate, cu cat baza este mai mare.

PROPRIETATI ALE FUNCTIEI EXPONENTIALE.

1) Functia exponentiala face sa-I corespunda sumei a doua numere reale produsul valorilor corespunzatoare ale functiei, adica: (x1+x2) = (x1) (x2), x1, x2 IR.
 


OBSERVATII. (x1 - x2) = (x1) / (x2);    (cx1) = ( (x1))c

2) Functia exponentiala este bijectiva si deci inversabila.
 

MONOTONIA FUNCTIEI EXPONENTIALE.

Daca a > 0, atunci (x) = ax este strict crescatoare;

0 < a < 1, atunci (x) = ax este strict descrescatoare.

 


OBSERVATIE. Pentru a > 1, ax1 < ax2 x1 < x2; Pentru 0 < a < 1, ax1 < ax2 x1 > x2.

SEMNUL FUNCTIEI EXPONENTIALE.

aI ) / , atunci (x) = ax > 0;

aI (0, 1) si    xI , 0), atunci (x) = ax I

xI ), atunci (x) = ax I

a > 1 si xI , 0), atunci (x) = ax    I

xI ), atunci (x) = ax I

 



Politica de confidentialitate | Termeni si conditii de utilizare



DISTRIBUIE DOCUMENTUL

Comentarii


Vizualizari: 7647
Importanta: rank

Comenteaza documentul:

Te rugam sa te autentifici sau sa iti faci cont pentru a putea comenta

Creaza cont nou

Termeni si conditii de utilizare | Contact
© SCRIGROUP 2024 . All rights reserved