Indicatorii tendintei centrale

1. Tipuri de medii

Media valorilor individuale ale unei variabile (caracteristici) statistice este expresia sintetizarii intr-un singur numar reprezentativ a tot ceea ce este esential, tipic si obiectiv in aparitia, manifestarea si dezvoltarea acestuia[1].

Deci, media este o valoare reprezentativa pentru un grup de date. Se pot defini mai multe tipuri de medie, dar cel mai frecvent utilizate sunt: media aritmetica, media armonica, media patratica si media geometrica. Diversitatea larga a fenomenelor social-economic, precum si complexitatea variabilitatii acestora, ne obliga sa alegem cu grija tipul de medie potrivit.

Media aritmetica, () se foloseste in general, cand fenomenul prezinta modificari aproximativ constante apropiate de forma unei progresii aritmetice.

Se calculeaza ca medie aritmetica simpla atunci cand numarul variantelor caracteristicii studiate este egal cu numarul unitatilor sau cand se cunoaste nivelul totalizat al caracteristicii si numarul unitatilor.

Daca notam cu X o caracteristica si cu x₁, x₂, .. , x_n variantele acesteia, atunci suma tuturor variantelor ne da nivelul totalizat al caracteristicii:

Substituim fiecare valoare x_i cu marimea medie a variantelor . Aceasta proprietate determinanta a mediei o vom utiliza la toate tipurile de medii care urmeaza sa le abordam.

Deci, facand substituirea tuturor nivelurilor individuale cu media lor, obtinem: 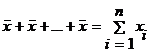, deci 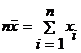, de unde:

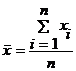(5.1)

Pentru seriile de distributie, cand variantele caracteristicii se inregistreaza de mai multe ori, deci apar frecventele se calculeaza ca medie aritmetica ponderata.

In aceasta situatia fiecarei variante a caracteristicii ii corespunde o anumita frecventa de aparitie, deci, suma variantelor se va face astfel:

Substituind nivelurile individuale cu media, obtinem:

de unde:

deci:

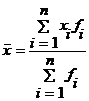(5.2)

Media aritmetica ponderata este deci influentata atat de nivelurile caracteristicii cat si de nivelul frecventelor.

Media aritmetica este marcata de o serie de proprietati dintre care o parte ajuta la verificarea exactitatii calculului iar altele determina modalitati de calcul simplificat al acesteia.

a)    Proprietatile de verificare a exactitatii mediei

a1) Media trebuie sa fie mai mare decat varianta minima si mai mica decat varianta maxima, adica:

(3.18)

a2) Suma abaterilor variantelor de la media lor este egala cu zero, adica:

- pentru media aritmetica simpla;

- pentru media aritmetica ponderata

b)      Proprietati de calcul simplificat:

- Media calculata din variantele caracteristicii micsorate in prealabil cu o constanta a este mai mica decat media reala cu constanta a, adica:

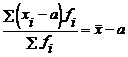, deci 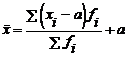(5.3)

- Media calculata din variantele caracteristicii micsorate in prealabil prin impartire la o constanta k, este mai mica decat media reala de k ori, adica:

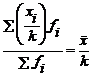, deci 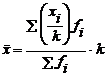(5.4)

Combinand cele doua proprietati (3.19) si (3.20) se obtine relatia de calcul simplificat al mediei aritmetice:

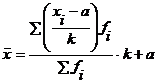(5.5)

Constantele a si k pot avea orice valoare, totusi se prefera ca acestea sa se aleaga pe baza seriei de distributie si anume:

a - varianta caracteristicii cu freventa cea mai mare;

k - marimea intervalului de variatie.

Rezulta din aceasta faptul ca relatia de calcul simplificat al mediei aritmetice se foloseste in cazul distributiilor cu intervale de variatie egale.

Simplificarea calculului consta in faptul ca odata stabilite valorile pentru a si k in cadrul seriei, pentru rapoartele se obtin valorile: 0 in dreptul lui a, -1,-2,etc deasupra si +1,+2 etc sub zero.

Exemplu: Sa se determine media aritmetica ponderata pentru urmatoarea serie de distributie aplicand cele doua metode de calcul:

Rezolvare:

Se construieste urmatorul tabel:

- metoda obisnuita:

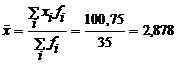
- calculul simplificat

Pentru aplicarea formulei de calcul simplificat se stabilesc:

a=2,75 - varianta corespunzatoare celei mai mari frecvente;

k=0,5 - lungimea intervalului de variatie.

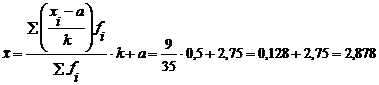
Se observa ca se obtine aceeasi valoare indiferent de metoda aplicata.

De retinut!

Principalul dezavantaj al folosirii mediei aritmetice consta in faptul ca ea depinde si de valori extreme ale seriei. Cand termenii seriei sunt imprastiati, ea devine nereprezentativa.

Semnificatia mediei aritmetice se pierde si in cazul in care in interiorul colectivitatii statistice, se observa manifestari distincte din punct de vedere calitativ. In astfel de situatii se recomanda gruparea colectivitatii pe clase de valori tipice, si calculul unor medii partiale pentru fiecare grupa in parte, dupa care se calculeaza o medie generala.

Media armonica, (), se foloseste atunci cand nu se cunosc frecventele f₁, f₂ ,,f_n si nici . Se deosebesc doua tipuri de medie armonica:

a)      Medie armonica propriu-zisa simpla sau ponderata;

b)     Medie armonica derivata din media aritmetica ponderata cunoscuta sub numele de medie armonica transformata a mediei aritmetice.

Media armonica propriu-zisa se calculeaza din valorile inverse ale termenilor seriei ca medie simpla sau ponderata.

Nivelul totalizator care intra in calculul mediei se obtine insumand valorile inverse ale variabilei X cu variantele astfel:

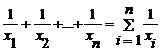
Substituind valorile individuale cu media lor armonica, se obtine:

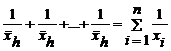, deci: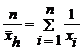

de unde:

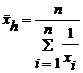- pentru serii simple de date. (5.6)

In cazul in care, fiecarei variante a caracteristicii si corespunde o anumita frecventa de aparitie, insumarea valorilor inverse se va face astfel:

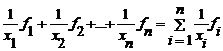
Inlocuind valorile individuale cu media lor armonica, obtinem:

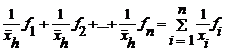
deci:

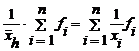
de unde:

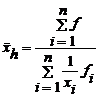- media armonica ponderata. (5.7)

Forma transformata a mediei aritmetice se foloseste atunci cand nu se cunosc frecventele f_i, dar se cunosc variantele si produsele f_ix_i.

In aceste conditii am putea determina frecventele astfel:

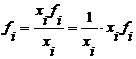
Daca in relatia de calcul a mediei aritmetice ponderate se inlocuiesc astfel frecventele f_i, se obtine media armonica. Se intalnesc totusi doua situatii:

1) Cand f₁x₁= f₂x₂== f_nx_n, caz in care se poate folosi direct media armonica simpla deoarece:

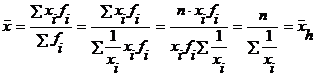(5.8)

2) Cand f₁x₁ f₂x₂ f_nx_n, caz in care se foloseste numai media armonica ponderata, adica:

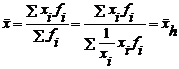(5.9)

Forma transformata a mediei aritmetice se foloseste la calculul nivelului mediu al unei caracteristici derivate cu caracter de marime medie partiala, sau marime relativa partiala.

De retinut!

O larga aplicabilitate o are pentru calculul pretului mediu si al indicelui mediu al preturilor. Media armonica ponderata propriu-zisa se foloseste ca model de calcul al indicelui mediu armonic.

Daca se compara cele doua medii (aritmetica si armonica), sesizam unele relatii utile in teoria si practica statistica, astfel:

daca termenii seriei sunt pozitivi ;

cand intre doua variabile interdependente exista un raport de inversa proportionalitate, el se pastreaza si in cazul mediilor calculate, deci nivelul mediu al uneia se calculeaza ca medie aritmetica, iar a celeilalte ca o medie armonica.

Exemplu: Sa se calculeze media armonica ponderata pentru urmatoarea distributie:

Rezolvare:

Se construieste urmatorul tabel:

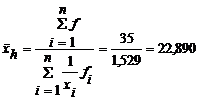
Exemplu: Sa se calculeze media armonica pentru urmatoarea distributie pentru care se cunosc produsele x_i f_i diferite intre ele.

Rezolvare:

Se construieste urmatorul tabel:

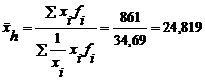
Media patratica , se foloseste in cazurile in care fenomenele inregistreaza cresteri aproximativ in progresie exponentiala, adica atunci cand cresterea este mai lenta la inceput si din ce in ce mai pronuntata spre sfarsit.

Ca medie se utilizeaza foarte rar, dar este folosita ca model de calcul al abaterii medii patratice, unul dintre indicatorii sintetici ai variatiei cu o larga utilizare. Se calculeaza din patratul valorilor unei variabile X.

In aceste conditii nivelul totalizator ce se ia in calculul mediei patratice, se prezinta astfel:

Inlocuind variabilele individuale cu media lor patratica, obtinem:

deci:

de unde:

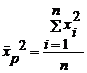
deci:

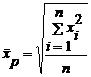- pentru serii simple. (5.10)

Daca fiecarei variante a caracteristicii si corespunde o frecventa atunci:

,

si inlocuind cu mediile avem:

deci:

de unde:

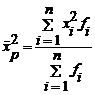sau: 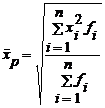(5.11)

- pentru serii cu frecvente (media patratica ponderata).

Exemplu: Sa se determine media patratica ponderata pentru urmatoarea serie:

Rezolvare:

Se construieste urmatorul tabel:

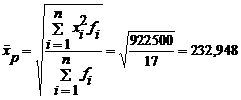
De retinut!

Media patratica se foloseste in statistica in situatii speciale si anume cand se da o importanta mai mare termenilor mari ai seriei (in cazul in care acestia predomina, seria fiind simetrica catre valori mari) sau in cazul in care termenii seriei au valori pozitive sau negative.

Media patratica este intotdeauna mai mare decat cea aritmetica. .

Media geometrica , Se foloseste in cazurile in care modificarile fenomenului se manifesta in progresie geometrica, adica atunci cand modificarile sunt mai mari la inceputul seriei si din ce in ce mai mici catre sfarsitul acesteia.

Ca model este utilizata in calculul indicelui mediu de crestere - indicator al seriilor cronologice deosebit de utilizat in analiza acestora.

Se bazeaza pe o relatie de produs intre valorile x₁, x₂, .. , x_n, ale unei caracteristici X, astfel:

Facand aceeasi substituire cu mediile obtinem:

,

deci:

,

de unde:

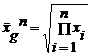- pentru seriile simple. (5.12)

Pentru seriile de frecvente:

dar substituind avem,

,

deci:

de unde:

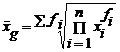- pentru seria cu frecventa. (5.13)

Pentru rezolvarea mediei geometrice, se utilizeaza logaritmii. Astfel ca formula de calcul a mediei geometrice ponderate devine:

sau (5.14)

Prin logaritmare se reduce variatia dintre termeni astfel incat valorile mai mici vor mai bine reprezentate in valoarea mediei.

Exemplu

Calculati media geometrica ponderata pentru urmatoarea serie de distributie:

Rezolvare:

Se construieste urmatorul tabel:

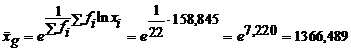
De retinut!

Media geometrica nu poate fi folosita daca in cadrul seriei, exista cel putin un termen negativ. Se foloseste pentru a calcula ritmul mediu de crestere (scadere) a unui fenomen in evolutia lui in timp. Media geometrica este mai mica decat media aritmetica calculata pentru aceeasi serie de date, .

2. Mediana si Modul

Mediana ( Me ) este acea valoare a caracteristicii care ocupa locul central al seriei statistice ordonate crescator sau descrescator.

Deci, mediana este acea valoare care imparte seria in doua parti egale.

a) In cazul seriilor simple se deosebesc doua situatii:

Seria are un numar impar de termeni, situatie in care mediana este acea varianta a caracteristicii cu rangul , n fiind numarul termenilor seriei, dupa ce in prealabil seria a fost ordonata;

Exemplul 6: Se da seria simpla cu 5 termeni (numar impar): 5, 6, 9, 2, 10.

Pentru determinarea medianei    se ordoneaza seria crescator: 2, 5, 6, 9, 10.

Se calculeaza rangul medianei==3. Mediana este egala cu varianta de pe pozitia 3 adica este Me=6.

Seria are un numar par de termeni, situatie in care mediana este data de semisuma termenilor centrali, dupa ce in prealabil seria a fost ordonata.

Exemplul 7: Se da seria simpla: 7, 9, 3, 12, 5, 8.

Se ordoneaza seria crescator:3, 5, 7, 8, 9, 12. Termenii centrali sunt 7 si respectiv 8. Mediana va fi: Me==7,5

b) In cazul seriilor de repartitie unidimensionale se dispune de doua modalitati de determinare a medianei:

Calculul algebric:

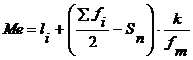(5.15)

unde:

l_i - limita inferioara a intervalului median;

- jumatate din colectivitatea statistica;

S_n - suma frecventelor ce preced intervalul median;

k - marimea intervalului de variatie;

f_m    - frecventa intervalului median.

Intervalul median este acel interval care cuprinde varianta centrala a sirului ordonat al variantelor seriei.

Exemplu: Se da seria de repartitie:

Mediana este valoarea ce imparte sirul ordonat al seriei in doua parti egale. Cum seria are 80 de termeni, rezulta ca mediana se gaseste practic intre varianta de pe pozitia 40 si cea de pe pozitia 41, deoarece semisuma frecventelor este =40

Deci, [2,4; 2,6] va fi intervalul median, deoarece acestui interval ii corespunde frecventa cumulata 48 ceea ce implica faptul ca variantele 40 si 41 din sirul ordonat se gasesc si ele in acest interval si implicit si mediana.

Mediana va avea valoarea:

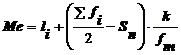= 2,4 + (40 - 16) . = 2,4 + 0,14 = 2,5 mil.lei

Se constata ca aceasta valoate se plaseaza in intervalul specificat, respectiv

Determinarea grafica:

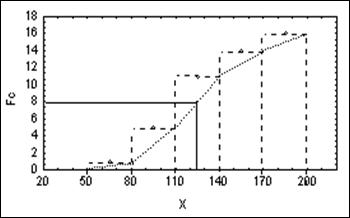
Se construieste poligonul frecventelor cumulate. De pe ordonata din dreptul lui se duce paralela la abscisa pana intersecteaza ogiva. Din aceasta intersectie se coboara perpendiculara pe abscisa, puncul gasit corespunzand valorii medianei.

Fig.5.1. Determinarea grafica a medianei

De retinut!

Mediana este una dintre variantele seriei statistice. Ea se bazeaza pe toate variantele seriei, dar numai sub aspectul numarului si pozitiei acestora;

Mediana poate fi folosita in locul mediei; Are utilizari largi in calculul unor indicatori ai asimetriei si mai ales este folosita pentru aprecierea semnificatiei mediei;

Cu cat diferenta este mai mica cu atat media este mai reprezentativa.

Modul este nivelul caracteristicii care are frecventa cea mai mare. Este cunoscut si sub numele de dominanta si se calculeaza numai pentru seriile de distributie.

In cazul seriilor de distributie unidimensionale se dispune, ca si in cazul medianei, de doua modalitati de calcul:

Calculul algebric

Se determina modul conform relatiei:

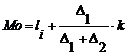(5.16)

unde:

l_i    - limita inferioara a intervalului modal;

D - diferenta dintre frecventa intervalului modal si frecventa precedenta;

D - diferenta dintre frecventa modala si frecventa urmatoare;

k    - marimea intervalului de variatie.

Intervalul modal este intervalul caruia ii corespunde frecventa cea mai mare.

Exemplu: Se da seria:

Intervalul modal este[2, 4; 2, 6]. (Intervalul corespunzator celei mai mari frecvente)

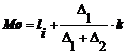= 2,4 + = 2,4 + 0,12 = 2,5

Determinarea grafica:

Are la baza histograma prin dreptunghiuri. Pentru determinarea modului se unesc punctele de incidenta a coloanelor adiacente cu varfurile superioare opuse coloanei modale si din intersectia celor doua segmente se coboara perpendiculara pe abscisa. Valoarea corespunzatoare punctului gasit prin intersectia perpendicularei cu abscisa este chiar modul.

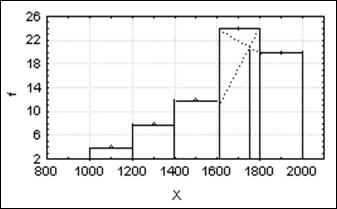
Fig.4.8. Determinarea grafica a modului

Modul este utilizat ca si mediana in calculul unor indicatori ai asimetriei.

De retinut!

In cazul distributiilor unimodale, ordinea intre cei trei indicatori ai tendintei centrale este de cele mai multe ori urmatoare: modul, mediana si media. Mediana inregistreaza chiar o apropiere de medie, comparativ cu pozitia sa fata de mod si numai in anumite cazuri mediana se situeaza mai aproape de mod decat de medie.

In cazul repartitiilor moderat asimetrice intre cei trei indicatori se stabileste urmatoarea relatie:

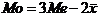(5.17)