Analiza capabilitatii proceselor de fabricatie

1. Concepte si definitii

2. Determinarea capabilitatii in cazul proceselor de "productivitate" medie (PM)

3. Determinarea capabilitatii in cazul proceselor de mare "productivitate" (MP)

Analiza capabilitatii proceselor de fabricatie

1. Concepte si definitii

Punerea in evidenta a abaterilor de la valorile normale ale parametrilor de calitate se face prin intermediul metodelor statistice ce au la baza o riguroasa fundamentare stiintifica. Sesizarea la timp a abaterilor de la valorile prevazute in specificatii (standarde de stat, de ramura sau de firma) cu ajutorul metodelor statistice permite depistarea si inlaturarea cauzelor perturbatoare din procesul de productie.

Este stiut ca variatia caracteristicilor de calitate intr-un proces de productie este rezultatul cauzelor de productie intamplatoare si sistematice.

Cauzele de productie sistematice ce actioneaza intr-o directie oarecare asupra parametrilor de calitate pot fii atribuite urmatoarelor surse:

-materia prima si materiale;

-utilajele prelucratoare (inclusiv SDV-urile);

-forta de munca;

-mediul ambiant.

Inlaturarea efectelor negative avute asupra parametrilor de calitate a produselor de cauzele de mai sus se poate face prin masuri organizatorice a productiei si muncii, respectarea tehnologiei de lucru.

Cauzele intamplatoare, sunt acele cauze care raman dupa eliminarea cauzelor sistematice, sunt greu de identificat, individualizat si masurat, pot actiona in toate sensurile, directiile de actionare supunandu-se intamplarii. Originea acestor cauze poate fi orice agregat, utilaj, variatia intrarilor din mediul inconjurator in sistemul de productie, etc.

Referitor la stabilitatea unui proces de fabricatie se poate afirma ca este:

-"static stabil" cand valorile caracteristici cercetate se distribuie static dupa o lege teoretica cunoscuta;

-"instabil" cand asupra procesului de fabricatie actioneaza una sau mai multe cauze de productie sistematice care influenteaza variatia caracteristicilor calitative;

-"dinamic stabil" cand valorile caracteristicii cercetate prezinta acelasi centru de grupare si aceiasi parametrii de imprastiere.

Variatia caracteristicilor calitative sub influenta fluctuatiilor procesului de productie formeaza "campul de imprastiere" (fig. 1). Acesta poate fi limitat inferior de valoarea l_i si superior de valoarea l_s, iar marimea acestuia reprezinta probabilitatea ca valorile caracteristicii sa fie cuprinse intre cele doua limite P(l_i<X<l_s). Evaluarea acestei probabilitati facandu-se cu legea distributiei normale sub forma normata:

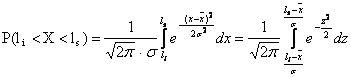
sau

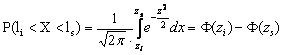
unde:

Daca distributia este centrata, limitele l_i si l_s sunt asezate la distante egale fata de medie, iar probabilitatea se poate scrie:

deoarece:

Limitele in interiorul carora este permisa variatia valorilor caracteristicii constituie limitele de toleranta care pot fii: TS -limita de toleranta superioara; TI -limita de toleranta inferioara.

Zona dintre aceste doua limite, in interiorul careia caracteristica poate varia fara ca prin aceasta calitatea produsului sa fie influentata se numeste "camp de toleranta" -TC.

Notiuni de baza referitoare la controlul statistic al procesului de fabricatie

1. Reglarea masinii, este caracterizata prin pozitia campului de imprastiere a valorii caracteristicii de calitate exprimata prin centru de grupare al distributiei. Reglarea este corespunzatoare cand centrul de imprastiere coincide (sau se afla in aceiasi zona) cu centrul campului de toleranta. Se utilizeaza pentru caracterizarea reglarii parametrii de pozitie: media , mediana x_me, valoarea maxima x_max, sau minima x_min, modulul x_mo, valoarea centrala a sirului de date x_c, etc.

2. Precizia masinii, reprezinta marimea campului de imprastiere a valorii caracteristicii Este considerata corespunzatoare cand marimea campului de imprastiere nu depaseste intervalul campului de toleranta (T=TS-TI). Ca parametrii ce caracterizeaza precizia masinii se considera: abaterea mediei patratice s, amplitudinea valorii caracteristicii R, abaterea medie absoluta a valorii A_m, coeficientul de variatie C_v, coeficientul de asimetrie b

Un proces tehnologic fata de reglare si precizie poate sa se gaseasca in urmatoarele situatii:

-stabil ca reglaj, atunci cand valoarea parametrului de grupare (, x_me, x_min, x_max) pentru caracteristica de calitate cercetata are valoarea neschimbata in timp;

-stabil ca precizie, cand procesul la care valoarea parametrului de imprastiere (s, R, A_m, C_v) ramane practic neschimbat in decursul unei perioade de timp;

-instabil ca precizie, este procesul in care actioneaza una sau mai multe cauze sistematice, care determina variatia unilaterala ca sens a valorilor caracteristicii. Instabilitatea dinamica a procesului consta ca nici una din valorile tipice ce caracterizeaza centrul de greutate sau imprastiere nu sunt constante.

Productia necorespunzatoare calitativ (rebutata) poate rezulta dintr-un proces necorespunzator ca reglare, ca precizie sau prin conjugarea ambelor cauze. Situatia productiei obtinuta dintr-un proces de productie se poate situa in una din urmatoarele pozitii reprezentate grafic in fig. 2.

Operatia de determinare a performantelor utilajelor de a realiza o incadrare a campului de imprastiere in campul de toleranta, in ipoteza reducerii la limita a influentelor sistmatice este cunoscut ca si studiul compatibilitatii (posibilit tehnique).

Studiile de compatibilitate sunt utilizate in practica in repartizarea sarcinilor pe masini si operatii, astfel incat pe agregatele cu posibilitati reduse de realizare a unui camp de imprastiere mic sa nu fie programate prelucrari care necesita o clasa de precizie ridicata si invers.

Ca masura statistica a capabilitatii este marimea intervalului de imprastiere a caracteristicii calitative. Deci masura capabilitatii indica intervalul previzibil al variatiei care poate va fi depasit, doar cu o mica probabilitate. Astfel in intervalul s sunt cuprinse 99,8% din valorile inregistrate intr-o observatie, in intervalul s, 95%, iar in intervalul s numai 68% din valori.

Intr-o exprimare sintetica, valoarea capabilitatii este data de relatia:

Valoarea sa se considera optima cand este situata intre 0,6.0,8.

In practica, pentru exprimarea capabilitatii se poate utiliza comparatia directa a marimii campului de imprastiere cu limitele specificate, astfel:

T=2z_ps

unde:

2. Determinarea capabilitatii in cazul proceselor de "productivitate" medie (PM)

In cadrul proceselor de "productivitate" medie (PM) formarea esantionului de studiu impune pentru asigurarea reprezentativitatii, prelevarea:

-individuala a probelor elementare (unitatilor de produs);

-in ordinea fabricatiei;

-fara intrerupere, pana la realizarea volumului de date propus pentru cercetare.

Aceasta metoda de efectuare a observarii este cunoscuta si sub denumirea de "metoda probelor mari".

O data esantionul prelevat se trece la masurarea caracteristicii urmarite, iar rezultatele sunt trecute in fisa de observatii

Din procesul tehnologic de productie se recolteaza un numar suficient de mare de exemplare (dupa uni autori n=40 60, dupa altii de minim 100 si maxim 300 unitati elementare, iar dupa altii n se calculeaza astfel ca abaterea medie de selectie fata de media generala a populatiei sa nu fie mai mare decat o valoare fixata a erorii limita exprimate in unitati ale abaterii medii patratice D s).Datele selectate se transpun intr-un sistem de axe obtinandu-se graficul de timp care permite evidentierea grupelor de valori distincte cu acelasi centru de grupare si aceeasi imprastiere.

Daca in perioada recoltarii probelor, reglarea si precizia masinii raman constante rezulta o singura grupa distincta, atunci valorile caracteristicii au o anumita repartitie denumita "repartitie instantanee".

In cazul cand graficul timpului semnalizeaza mai multe grupe de valori ale caracteristicii analizate in timp se pune problema determinarii repartitiei experimentale a fiecarei grupe, se calculeaza de asemenea parametrii de centrare si de imprastiere.

Obs. Impartirea valorilor caracteristicii in grupe distincte, pe baza graficului de timp, contine o doza destul de mare de subiectivitate in sensul ca pot fi atribuite unei grupe de valori care de fapt apartin altei grupe, caracterizata printr-un alt centru de grupare si o alta imprastiere. Pentru solutionarea acestei probleme este necesara mai intai verificarea omogenitatii datelor prelevate si, daca este cazul, omogenizarea lor prin excluderea valorilor care se abat semnificativ de masa tuturor valorilor.

2.1. Verificarea omogenitatii datelor observate

Din numeroasele teste folosite in acest scop (testul van de Waerden, criteriul semnelor, criteriul Wallis-Moore, metoda iteratiilor, testele Wilcoxon, Smirnov si altele) in continuare se va trata metoda iteratiilor, care consta in gruparea valorilor prelevate in valori mai mici si mai mari decat unul din parametrii de grupare (mediana)

Valorile succesive care au aceiasi proprietate, adica sunt fie mai mari fie mai mici decat mediana, formeaza o iteratie. Numarul valorilor care compun o iteratie constituie lungimea iteratiei. Daca in timpul efectuarii operatiei de prelevare a datelor au actionat numai cauze intamplatoare de productie, deci datele sunt omogene, vom avea un numar mare de iteratii de lungime mica. Cu ajutorul iteratiilor se pot construi teste, pe baza numarului total al iteratiilor, fie pe baza lungimii lor.

In continuare se va utiliza "criteriul numarului total al iteratiilor"

Conform acestui criteriu, daca volumul esantionului este suficient de mare, numarul iteratiilor R se distribuie dupa o lege normala cu parametrii: Media , dispersia , in cazul cand n₁=n₂=n/2, (unde n₁ reprezinta valorile mai mici decat media si n₂ mai mari decat media sirului prelevat).

In cazul cand productia este sub influenta cauzelor intamplatoare, rezulta ca numarul R va depasi o anumita valoare teoretica R_a teoretic sa fie mica: P(R<R_a a

Daca in momentul prelevarii produselor, procesul tehnologic se afla sub influenta cauzelor de productie intamplatoare, deci repartitia valorilor este aleatoare, atunci numarul de iteratii R va depasi o anumita valoare teoretica R_a, determinata astfel incat probabilitatea ca R calculata sa nu depaseasca R_a teoretic sa fie mica:

P(R< R_a a£

Daca numarul de iteratii se distribuie aproximativ normal rezulta:

P(R<R_a)=P(z<z_a)=1/2

Variabila z este definita ca:

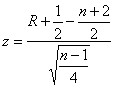
Rezulta in final:

Aceiasi problema se poate rezolva si cu ajutorul "criteriului lungimii iteratiilor". Si lungimea iteratiei este o variabila aleatoare care, pentru un volum suficient de mare al esantionului, se repartizeaza dupa legea Poisson, tinzand catre legea normala pe masura cresterii lui n.

Daca datele obtinute prin controlarea produselor prelevate sunt independente, deci in proces au actionat numai cauze de productie intamplatoare, atunci lungimea iteratiei nu poate depasi o valoare calculata k_a, determinata in asa fel incat P(k-k_a

Utilizand legea de repartitie Poisson, in care media este:   se obtine valoarea limita a lungimii iteratiei, egala cu:

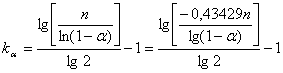
Daca ce mai mare iteratie a problemei are o lungime inferioara valorii k_a, se poate concluziona ca materialul statistic cules este omogen, ca procesul de productie s-a aflat in timpul cercetarii numai sub influenta cauzelor de productie intamplatoare.

Un alt test pentru verificarea omogenitatii datelor observate, cu certe avantaje fata de cel al iteratiilor, este testul "Wallis-Moore". Avantajul acestui test consta in faptul ca nu necesita mai intai calcularea unui parametru statistic si apoi compararea tuturor valorilor observate cu acest parametru, ci comparatiile se efectueaza intre valorile succesiv observate.

Aplicarea testului presupune mai intai reprezentarea pe un grafic timp a datelor. Se identifica in continuare "punctele critice" incadrate cu doua valori inferioare sau superioare, apoi se determina lungimea "fazelor" (faza reprezinta distanta intre cele doua puncte critice alaturate). Testul consta in a verifica daca numarul de puncte critice si distributia lungimii fazelor sunt compatibile cu ipoteza caracterului intamplator al repartitiei.

Pentru criteriul punctelor critice, daca rezultatele obtinute in cercetare reprezinta probe independente, numarul h al punctelor critice urmeaza o lege de repartitie de tip normal. Pentru valoarea parametrului h se poate construi si un interval de incredere ale carui limite sunt:

M(h) si s(h) reprezintamedia si respectiv abaterea medie patratica a numarului punctelor critice h, care se calculeaza astfel:

unde: n -volumul esantionului cercetat

z_a -valoarea tabelara a functiei Laplace pentru un nivel de semnificatie a stabilit

2.2. Omogenizarea datelor

Pentru rezolvarea acestei probleme, denumita frecvent "eliminarea valorilor aberante", exista o clasa de teste dintre care cel mai cunoscut este testul Grubbs-Smirnov.

Testul permite identificarea si apoi eliminarea valorilor suspecte ca "aberante" sau "intruse" si care de fapt, dintr-un motiv sau altul, nu apartin populatiei de baza din care provine masa celorlalte valori.

Fie un sir de observatie: x₍₁₎, x₍₂₎, ., x_(n), unde x₍₁₎ si x_(n) reprezinta ce mai mica, respectiv cea mai mare valoare observata.

Functia de repartitie a valorii maxime x_(n) este

P(x_(n)£x)=[P_(x)]ⁿ=P

unde: P(x)=P(X£x)=P₁ reprezinta functia de repartitie a caracteristicii X

Daca se fixeaza o probabilitate P, atunci exista o valoare maxima x_(n)p care nu nu poate fi depasita decat cu o probabilitate mai mica (de exemplu a£

Daca caracteristica X se raporteaza normal (M[X]=m, Dd[X]=s ), se poate defini o variabila:

pentru o anumita valoare P rezulta valoarea maxima teoretica a unui sir de observatii:

unde P₁=0,5+F(z_p1), iar valoarea minima va fi

Daca valoarea maxima a sirului de observatii x_(n) este mai mica decat valoarea teoretica x_(n)p, se considera ca valoarea ei mare este datorita intamplarii, iar daca x_(n)>x_(n)p, valoarea ser exclude din calculele viitoare, ca fiind o abatere grosolana de la sirul celorlalte valori.

Asemanator, se poate detremina un criteriu pentru excluderea valorilor minime dintr-un sir de observatii. Tinand seama de simetria repartitiei normale, rezulta ca valoarea z_(n)P1 este egala si de semn contrar cu valoarea z_(n)P, deci limita teoretica minima este:

Daca cea mai mica valoare din sirul de observatii x₁ este mai mica decat x_(1)p se va elimina, ea reprezentand o abatere puternica de la sirul valorilor observate, daca este mai mare sirul este acceptabil.

In cazul cand pentru m si s nu sunt cunoscute valorile, este necesara estimarea lor pe baza unui esantion, valorile critice (maxime si minime) se determina cu relatiile:

si

unde :

Daca tpate observatiile x₍₁₎, x₍₂₎, ., x_(n) sunt extrase din aceeasi populatie, normal repartizata, atunci repartitia variabilei v_p nu depinde de m si s ai populatiei, ci de marimea probei n

In practica se pot intalni si alte situatii in legatura cu cunoasterea sau nu a unor parametri, acestea sunt prezentate in tabelul urmator

Calculul limitelor pentru eliminarea valorilor aberante

Exemplu

Fie valorile masurate ale diametrului, (mm), unui ax prezentate in tabelul nr. 1

Tabelul nr. 1

Se cere sa se arate ca datele din tabel sunt omogene

Valorile urmatorilor parametrii statistici sunt: Media m=49,9421, mediana Me=49,93; s

Avand datele din tabelul 1 se detemina: media =49,9421, s

Cunoscand valorile celor doi parametri se trece la rezolvarea problemei referitoare la omogenizarea materialului statistic. Cea mai mare valoare din sir este x_max=50,2, cea mai mica valoare este x_min=49,62, iar marimea probei n=100

Limita superioara a variatiei va fi:

Pentru n=100 si P=0.99 din tabele citim =4,26

Intrucat x_max=50,2<x₍₁₀₀)_P=50,437282, vom decide ca sirul valorilor observate este omogen din punct de vedere al valorii maxime)

Limita inferioara a variatiei va fi:

Deoarece valoarea minima observata x_min=49,62 depaseste valoarea minima calculata   se concluzioneaza ca datele prelevate formeaza o populatie omogena

2.3. Constructia repartitiei experimentale

Consta din urmatoarele etape:

1. ordonarea sirului;

2. stabilirea marimii intervalului de grupare cu relatia lui Sturges

3. stabilirea limitelor inferioara si superioara a fiecarei grupe sau clase;

4. reprezentarea grafica a datelor grupate in histograme sau poligonul frecventelor;

5. analiza reprezentarii grafice in vederea stabilirii legii de repartitie, odata stabilita legea se verifica cu ajutorul unui test analitic

2.4. Determinarea fractiunii defective probabile

Analiza desfasurarii procesului tehnologic are drept scop cunoasterea posibilitatilor utilajelor din punct de vedere al centrului de reglare si al preciziei.

Precizia utilajelor tehnice trebuie caracterizata in stransa legatura cu marimea campului de toleranta. In legatura cu tolerantele se poate afirma ca este fractiunea defectiva probabila, parametru cunoscut si sub denumirea de indicatorul sau parametrul preciziei.

Parametrul preciziei reprezinta probabilitatea ca valorile caracteristicii X sa se plaseze in afara campului de toleranta fig. 3

Fractiunea defectiva p se obtine cu relatia:

p=P(X<TI; X>TS)

sau

p=1-P(TI£X£TS)

Daca folosim functia de repartitie rezulta:

p=1-[P(X£TS)-P(X³TI)]=1-[F(TS)-F(TI)]

Utilizand frecventa f(x) se obtine:

Cand caracteristica este normal repartizata, fractiunea defectiva probabila se determina cu relatia (fig. 4):

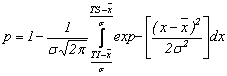sau cu ajutorul functiei Laplace:

p=1-[F(z_p)-F(z_i)]

iin care:

Tinand seama ca limitele de toleranta TI si TS sunt simetrice fata de centrul campului, iar centrul campului de toleranta coincide cu centrul campului de imprastiere, z_s=|z_i|=z sau z_i=-z si z_s=z caz in care fractiunea defectiva probabila va fi:

p=1-2F(z)

unde:

In functie de valoarea acestui parametru se apreciaza capabilitatea procesului, starea procesului, raportul dintre tolerantele impuse prin specificatii si probabilitatea procesului de incadrare in limitele impuse, concluzionandu-se daca procesul tehnologic analizat poate fi dirijat prin metodele statistico-matematice, si ce anume metoda de dirijare pot fi utilizate.

Standardele in vigoare recomanda un proces ca fiind controlabil static, cand 0,001£p£0,02. Cand p<0.001 precizia este necorespunzatoare, procesul fiind in acest caz necontrolabil.

In tabelul nr. 1 caracteristica urmarita este 49,95 deci T=0.60, abaterea medie patratica s=0,116424. Rezulta z. Din tabelul Laplace aflam F(2,5808671)=.. Deci p=1-(2 )= sau p=