| CATEGORII DOCUMENTE |
| Comunicare | Marketing | Protectia muncii | Resurse umane |
CONDUCEREA SI CONTROLUL STOCURILOR
In orice problema de stocuri intervin :
- o cerere de consum articole din stoc care este in general aleatoare functie de timp ,dar care poate fi determinata ;
- un stoc necesar pentru satisfacerea cererilor si care periodic este reaprovizionat ;
- costuri de depozitare (deprecieri , manipulare , asigurari , demodare , furturi ) de aprovizionare ( forta munca , formulare , telefoane , transport , deplasari ) si de penurie .
Presupunem ca intervalul de timp dintre darea comenzii de reaprovizionare si receptia materialului este nul . Se disting doua metode principale de gospodarire a stocurilor :
a)
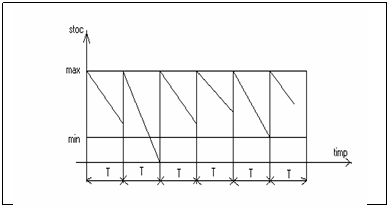
metoda periodica ,
adica la intervale egale ;
Metoda este usor de aplicat , dar exista riscul epuizarii stocului .
b) metoda de relaxare sau comenzi in cantitati constante .
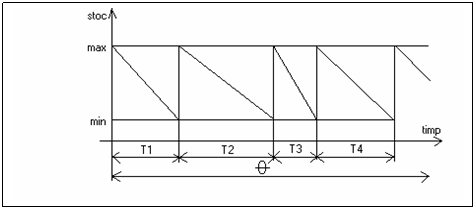
Metoda evita riscul epuizarii stocului , dar este mai greu de realizat , stocul trebuie supravegheat permanent .
Definitie : Intervalul de timp intre emiterea comenzii de reaprovizionare si primirea materialelor se numeste timp de reaprovizionare notat cu τ si presupus constant .
In prima metoda
momentul lansarii comenzii este
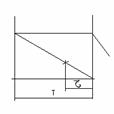
cunoscut , dar trebuie estimata cantitatea de aprovizionat
deoarece nu este cunoscut consumul care va fi inregistrat
de la lansarea comenzii pana la sosirea materialelor . In a
doua cunoastem cantitatea de reaprovizionat , dar nu este
cunoscut momentul lansarii comenzii.
Reaprovizionarea se face pe loturi de marime n , costul unei reaprovizionari Cr fiind independent de marimea lotului .Costul stocarii unei unitati de stoc pe unitatea de timp este Cs . Cererea totala in intervalul θ este N .
Se cere marimea lui n astfel ca totalul costurilor sa fie minim .
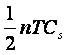
Nivelul mediu al stocului in
intervalul T este este n/2 , costul stocarii in intervalul T este :
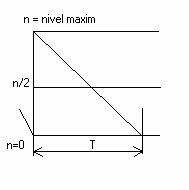
Numarul de reaprovizionari in intervalul θ
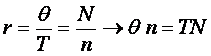 este
:
este
:

Expresia F(n) se poate reprezenta grafic in functie de n punand in evidenta cele doua componente: costul de reaprovizionare si costul de stocare
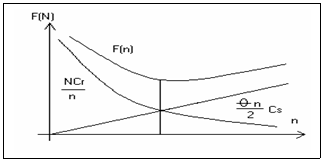
Minimumul lui F(n) se obtine din egalarea derivatei a I-a cu zero .

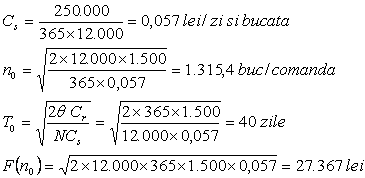
Exemplu : Un atelier
confectioneaza rame pentru CED si BLA . Cantitatea de relee folosite anual este
de N = 12.000 buc.Cheltuielile cu depozitarea sunt de 250.000 lei/an .
Cheltuielile pentru o comanda sunt de Cr = 1.500 lei . Nu se admite ruptura de stoc .
B. Lotul economic cand se admite epuizarea stocului
In acest caz stabilim un cost de penurie Cp , care poate fi paguba suferita , sau daca este vorba de lansarea in fabricatie penalizarea platita .
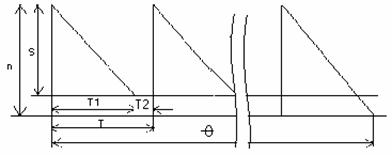
notam: S - nivelul maxim al stocului ;
T - intervalul cind se consuma din stocul existent ;
T - intervalul lipsa stoc , consumul se satisface din lotul urmator .
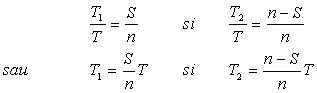
Din desen se observa
ca prin asemanare de triunghiuri exista relatiile :
![]()
Atunci : - costul stocarii unui lot este ;
![]() - costul
reaprovizionarii(sau livrarii) Cr
- costul
reaprovizionarii(sau livrarii) Cr
- costul de penurie unde :
Cp - costul de penurie pe unitatea de stoc si unitatea de timp .
![]()
Costul total este :
![]()
r - numarul loturi lansate sau de
reaprovizionari .
![]()
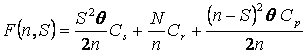
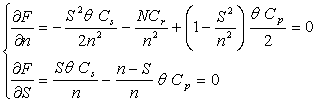
Se afla valorile lui n si S pentru care F(n, S) este minim egaland derivatele partiale cu
zero .
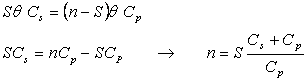
Din ultima relatie rezulta n functie
de S

Din prima relatie rezulta :

Inlocuim pe n , efectuam si obtinem valoarea optima
pentru S:
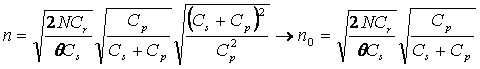
Calculam valoarea optima al lui n stiind pe S:

Costul total optim se obtine
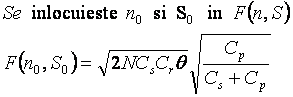
![]() Se noteaza cu numit indice de lipsa.
Se noteaza cu numit indice de lipsa.
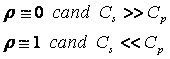
Acesta variaza
intre: 0 ≤ ρ ≤ 1 .
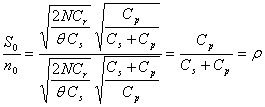
Cand Cp → ∞ admitem apriori ca stocul nu trebuie
sa se epuizeze . Se remarca ca
daca se face raportul :
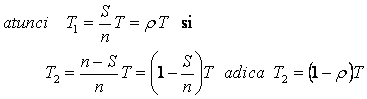
Ultima expresie arata ca in intervalul T exista posibilitatea sa se produca epuizarea stocului de (1-ρ) ori la % . Altfel exprimat (1-ρ) este probabilitatea ruperii stocului .

![]() Comparand formulele de calcul in cele
doua ipoteze cu si fara epuizarea stocului , se remarca ca primele se
corecteaza cu , adica :
Comparand formulele de calcul in cele
doua ipoteze cu si fara epuizarea stocului , se remarca ca primele se
corecteaza cu , adica :

Reluam exemplul anterior in ipoteza costului
de penurie (penalizarea) in valoare de:
Practic este anevoios a se tine aceasta evidenta pentru tot nomenclatorul de produse si se aleg numai cele care au pondere valorica mare mai ales ca si in domeniul gestiunii stocurilor este aplicabil principiul lui Pareto. Adica intre ponderile procentuale a numarului de repere sau sortotipodimensiuni din stocurile unei intreprinderi si ponderea procentuala valorica a acestora exista relatia:
% nr. repere % valoare
15
5 40
20 70
60 95
Pe baza acestei constatari se intocmeste diagrama ABC .
Se
disting cele 3 regiuni:
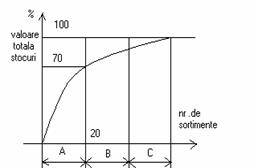
A: numar mic de sortimente cu
pondere valorica ;
C: numar mare de sortimente cu
Pondere valorica mica .
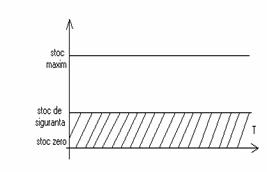
In practica se mai utilizeaza metoda de conducere a stocurilor cu stoc de siguranta , sau denumita si metoda celor "doua magazii" .
In momentul cand s-a epuizat stocul din prima magazie se face comanda de reaprovizionare si se consuma din cea de a doua .
Dat fiind numarul mare de fise de stoc la o regionala de cale ferata de cca. 120.000 din care cca. 30.000 diferite si numarul mare de intrari iesiri din stoc (miscari) de cca.60.000 lunar , evidenta gestiunii stocurilor este tinuta pe calculator.
Acelasi model matematic se poate folosi si in cazul deciziei asupra lotului economic de productie. Sa presupunem ca un fabricant produce mai multe produse pe aceiasi linie de fabricatie. Schimbarea produsului fabricat necesita intreruperea productiei pentru schimbarea, inlocuirea SDV - urilor (scule dispozitive verificatoare) pentru noul produs, difuzarea noilor fise tehnologice, reglarea masinilor etc. Toate acestea reprezinta costuri suplimentare. Pentru evitarea lor o strategie ar fi sa se schimbe produsul cat mai rar si sa se creieze stocuri astfel ca livrarile sa fie facute din stoc. Dar si productia pe stoc aduce costuri suplimentare de depozitare, conservare, imobilizarea fonduri, riscuri de depreciere etc. Astfel ca se pune problema sa se gaseasca lotul economic produs care face ca pe total costurile sa fie minime. Modelul matematic care raspunde acestei cerinte este exact cel prezentat pentru gestiunea stocurilor.
Ackoff & Sasieni, Bazele cercetarii operationale, Ed. Tehnica, Bucuresti 1975.
Isaic-Maniu Al., In cautarea optimului, Ed albatros, 1985.
Kaufmann A., Metode si modele ale cercetarii operationale Vol 1 si 2, Ed. Stiintifica, Bucuresti, 1967.
Malita M, Zidaroiu C. Matematica organizarii. Editura tehnica. Bucuresti 1975.
Maynard, H.B, Manual de inginerie industriala. , Ed. Tehnica, Bucuresti 1975.
Starr M.K., Conducerea productiei. Sisteme si sinteze, Ed. tehnica, Bucuresti, 1970
Vaduva I, Dinescu C, Savulescu B, Modele matematice de organizare si conducerea productiei, vol.1 si 2, Ed. Didactica si Pedagogica Bucuresti. 1974
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 3798
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2025 . All rights reserved