Masurarea riscului in afaceri

Masurarea riscului in afaceri

Pentru ca riscul sa poata fi masurat trebuie sa i se atribuie o valoare, adica sa i se asocieze o masura a distributiei de probabilitate. O Astfel de masura este deviatia standard. Cu cat este mai restransa distributia de probabilitate cu atat este mai mica deviatia standard, iar riscul afacerii (proiectului) este mai mic. In acest context riscul poate fi definit prin probabilitatea ca rentabilitatea sa fie mai mica decat cea asteptata (estimata) si nu prin intreaga distributie de probabilitate. Pentru determinarea deviatiei standard trebuie parcurse urmatoarele etape:

a) Calcularea ratei estimate a rentabilitatii (R_er):

In exemplul luat pentru proiectul "X" al firmei Alfa s-a determinat o rata estimata a rentabilitatii de 29%;

b) Obtinerea unui set de deviatii (∆_i) a ratei estimate a rentabilitatii prin scaderea ratei estimative a rentabilitatii din fiecare varianta a ratei de rentabilitate asteptate potrivit relatiei de calcul:

unde,

∆_i - deviatia variantei i;

r_i - rata de rentabilitate asteptata a variantei i;

R_er - rata estimata a rentabilitatii;

i - varianta scenariului alternativ.

c) Determinarea variantei distributiei de probabilitate prin insumarea produselor obtinute intre probabilitatea variantei si un alt termen  reprezentand deviatia standard ridicata la patrat;

Relatia de calcul a variantei distributiei de probabilitate este:

unde,

ds² - variatia distributiei de probabilitate;

∆_i - deviatia variantei i;

p_i - probabilitatea asociata variantei i;

i - varianta scenariului alternativ;

n - numarul de variante.

d) Stabilirea deviatiei standard, prin relatia de calcul:

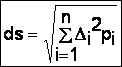unde,

ds - deviatia standard;

∆_i - deviatia variantei i;

p_i - probabilitatea asociata variantei i;

i - varianta scenariului alternativ;

n - numarul de variante.

Continuand exemplul dat, calculul deviatiei standard a proiectului "X" al firmei Alfa va fi:

respectiv 15,23%.

Prin urmare deviatia standard este o probabilitate, adica media ponderata a deviatiei de la valoarea asteptata, indicandu-se cu cat este mai mica sau mai mare valoarea reala a riscului fata de valoarea asteptata. In exemplul luat, deviatia standard a proiectului "X" al firmei Alfa este 15,23%.

In ipoteza in care distributia de probabilitate este continua se pot uni ratele rentabilitatii asteptate trasate grafic pentru proiectele "X" si "Y" a firmei Alfa, rezultand urmatoarea reprezentare grafica:

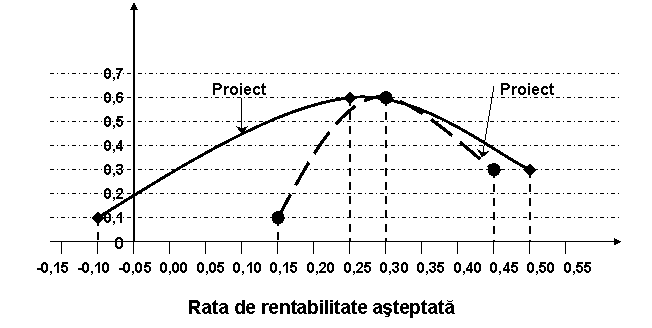
Analizand cele doua reprezentari grafice rezulta ca proiectul "Y" desemneaza o investitie mai favorabila, intrucat distributia de probabilitate este mai redusa, dispersia este mai mica, reflectand un risc mai mic.

Pentru o masurare mai buna a riscului se utilizeaza coeficientul de variatie

(K _v) a proiectului dat de relatia de calcul:

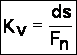unde,

K _v - coeficientul de variatie a proiectului;

ds - deviatia standard a proiectului;

F_n - fluxul de numerar preconizat pentru proiectul in cauza.

Exemplu Consideram ca:

pentru  proiectul "X" se preconizeaza un profit asteptat de 20000 mii EURO in conditiile unei deviatii standard exprimata in EURO de 11 000 mii EURO.

pentru proiectul "Y" se preconizeaza un profit asteptat de 80 000 mii EURO si o deviatie standard exprimata in EURO, egala cu cea a proiectului "X", anume de 11 000 mii EURO.

Potrivit situatiei date, coeficientii de variatie a celor doua proiecte sunt:

la proiectul "X":;

la proiectul "Y":;

In baza celor prezentate mai sus, proiectul "X" este mai riscant decat proiectul "Y", avand un coeficient de variatie mai mare. Cu alte cuvinte, pentru fiecare EURO din profit, proiectul "X" prezinta un risc mai mare decat proiectul "Y", desi deviatiile standard sunt la fel.

De regula, coeficientul de variatie se utilizeaza cand se face apel la evaluarea profitului in valori absolute (in exemplul luat in EURO), situatie in care se impune o corectie a deviatiei standard cu marimea fluxului de numerar. Daca se face apel la rata de rentabilitate nu este necesara utilizarea coeficientului  de variatie, intrucat rata de rentabilitate nefiind exprimata in valori absolute (EURO) este independenta de marimea fluxului de numerar.