Metode si tehnici de fundamentare a deciziilor

Metode si tehnici de fundamentare a deciziilor

1 Optimizarea deciziilor in conditii de certitudine

Deciziile in conditii de certitudine pot fi optimizate dupa un singur criteriu sau folosind mai multe criterii. In situatia folosirii unui singur criteriu se impune utilizarea criteriului cel mai important pentru situatia decizionala respectiva. Alegerea criteriului cel mai important presupune o ierarhizare a acestora, folosindu-se in acest scop o matrice de selectie a criteriilor, dupa modelul prezentat in tabelul 4.2.

Tabelul 4.2

Matricea de selectie a criteriilor

Matricea de selectie a criteriilor se intocmeste respectand urmatoarele reguli:

criteriile se compara unul cate unul;

daca, de exempu, un criteriu A este mai important decat un alt criteriu, de exemplu B, atunci pe coloana corespunzatoare criteriului A, la intersectia cu linia corespunzatoare criteriului B, se trece cifra 1, iar pe coloana lui B, la intersectia cu linia A, se trece cifra 0;

pe diagonala matricei se trece cifra 1;

nivelul total de importanta al fiecarui criteriu se obtine prin insumarea cifrelor trecute pe coloane.

Criteriul cu nivelul de importanta cel mai mare va fi folosit in alegerea variantei optime.

Fundamentarea complexa a deciziilor firmelor impune folosirea mai multor criterii decizionale. In conditiile mai multor criterii decizionale, deci a unor consecinte care pot fi exprimate prin unitati de masura diferite, poate fi folosita utilitatea ca masura a gradului in care o varianta este preferabila alteia. Se impune deci, problema transformarii tuturor consecintelor in utilitati care sa ierarhizeze corect variantele decizionale.

In sensul dat de J. von Newmann si O. Morgenstern, utilitatea ia valori in intervalul [0,1] astfel: u(V_i) = 1 daca varianta V_i este cea mai avantajoasa pentru decident potrivit unui anumit criteriu si u(V_j) = 0, daca varianta V_j este cea mai dezavantajoasa pentru decident, potrivit criteriului respectiv. De asemenea, pot exista si relatiile:

u(V_i) > u(V_j), cand varianta V_i este preferata variantei V_j;

u(V_i) = u(V_j), cand cele doua variante sunt echivalente.

Stabilirea utilitatilor prin metoda interpolarii liniare intre 0 si 1, in cadrul unui proces decizional se poate face astfel:

Notam cu:

V₁ - varianta cu utilitate maxima (u=1);

V₀ - varianta cu utilitate minima (u=0);

V_i - varianta i;

C_j - criteriul j;

a_j¹ - consecinta cea mai favorabila in criteriul C_j;

a_j⁰ _- consecinta cea mai nefavorabila in criteriul C_j;

a_ij - consecinta variantei v_i in criteriul c_j;

u_ij - utilitatea variantei V_i in criteriul C_j.

Pentru orice criteriu C_j, determinarea utilitatilor se face pornind de la ecuatia dreptei:

Y = AX + B

in care: Y - utilitatea;

X - consecintele

A si B - constante.

Relatia se foloseste pentru urmatoarele criterii:

a)      pentru criteriile de maxim, care au valori cu atat mai bune cu cat sunt mai mari.

- pentru varianta V₁ : 1 = Aa_j¹ + B

- pentru varianta V₀ : 0 = Aa_j⁰ + B

Din sistemul format din cele doua ecuatii rezulta A si B astfel:

A =  

B =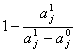  

Cunoscand pe A si B, se poate determina in continuare utilitatea oricarei variante in cadrul aceluiasi criteriu, astfel:

U_ij= Aa_ij+ B

U_ij =

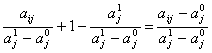
Deci:

U_ij =

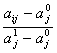
Relatia mai poate fi scrisa astfel:

U_ij =

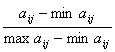
b)      pentru criteriile de minim, care au valori cu atat mai bune cu cat sunt mai mici

- pentru varianta V₁: 1 = Aa_j⁰ + B

- pentru varianta V_0: 0 = Aa_j¹ + B

Ca si in cazul precedent, constantele A si B rezulta din rezolvarea sistemului format din cele doua ecuatii:

A =

B =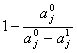  

Utilitatea oricarei variante U_ij va fi data de relatia:

U_ij = Aa_ij + B

U_ij =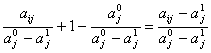

Deci:

U_ij =  

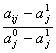
Relatia poate fi scrisa si astfel:

U_ij =  

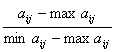
Alegerea variantei optime dupa mai multe criterii impune ierarhizarea acestora prin stabilirea importantei fiecarui criteriu pentru firma intr-o anumita etapa de dezvoltare a acesteia. Criteriile se pot ierarhiza prin acordarea de catre decident a unor coeficienti de importanta (K_j) incadrati intr-un anumit interval, de exemplu [0,1].

1.1 Metoda utilitatii globale

Forma generala a consecintelor unei decizii optimizate dupa mai multe criterii este prezentata in tabelul 4.3.

Tabelul 4.3

Consecintele deciziei optimizate dupa mai multe criterii

Coeficientii de importanta ai criteriilor pot fi identici sau diferentiati.

In conditiile unor coeficienti de importanta ai criteriilor identici (care au valori egale), potrivit acestei metode, varianta optima corespunde aceleia pentru care suma utilitatilor este maxima, adica:

V_opt =

unde: U_ij reprezinta utilitatea variantei i dupa criteriul j.

Daca valoarea coeficientilor de importanta este diferita pentru criteriile decizionale, varianta optima este aceea pentru care suma produselor dintre utilitati si coeficienti de importanta este maxima, adica:

V_opt =

1.2 Metoda ELECTRE

Metoda ELECTRE ( Elimination et Choix Traduisant la Realit), care in traducere inseamna " Metoda de clasament si alegere in prezenta unor puncte de vedere multiple", a fost conceputa de Bertrand Roy in anul 1967. In aceasta metoda varianta optima este aceea care surclaseaza celelalte variante.

Metoda comporta urmatoarele etape:

a) Calculul utilitatii variantelor pentru fiecare criteriu de optimizare a deciziei si atribuirea coeficientilor de importanta pentru criteriile folosite in optimizarea deciziei se face ca in metoda utilitatii globale.

b)Calculul coeficientilor de concordanta si discordanta ai alternativelor decizionale si completarea matricelor acestor coeficienti.

Coeficientii de concordanta se calculeaza dupa relatia:

C( V_g, V_h) =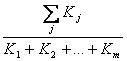  

in care:

- - suma coeficientilor de importanta ai criteriilor pentru care se respecta restrictia U(V_g)U(V_h);

- K_i(I=1,m) - coeficienti de importanta ai criteriilor considerate;

- C(V_g,V_h) - coeficientul de concordanta intre varianta g si varianta h.

Coeficientii de concordanta au valori cuprinse intre 0 si 1 si arata cu cat o varianta V_g depaseste o alta varianta V_h.

Coeficientii de discordanta se calculeaza dupa relatia:

0, daca U(V_g)U(V_h)

D(V_g, V_h) =

|U(V_g) - U(V_h)|, pentru U(V_g)<U(V_h)

Unde: D(V_g,V_h) - coeficientul de discordanta intre varianta g si varianta h.

U(V_g), U(V_h) - utilitatea variantei g, respectiv a variantei h

E - ecartul maxim intre utilitatea minima si cea maxima (E=1)

Coeficientii de discordanta au valori cuprinse intre 0 si 1 si arata cu cat o alternativa V_h depaseste o alternativa V_g.

c)      Alegerea variantei optime pe baza relatiilor de surclasare a variantelor cu ajutorul coeficientilor de concordanta si discordanta se introduce o relatie de surclasare, dupa care varianta V_g surclaseaza varianta V_h daca se satisfac in acelasi timp relatiile:

C(V_g,V_h)

D(V_g,,V_h) ,

unde p si q sunt valori limita alese de decident, cu nivelul intre 0 si 1. Initial se atribuie lui p valoarea 1 si lui q valoarea 0, iar in continuare se diminueaza p si se majoreaza q pana cand o varianta surclaseaza pe toate celelalte. In cazul in care se satisfac cele doua relatii (5.32), varianta g surclaseaza varianta h. Din relatiile de surclasare rezulta o serie de grafuri G(p,q), asociate acestora, din care se deduce varianta optima. Varianta optima este aceea care surclaseaza toate celelalte variante, surclasarea fiind cu atat mai puternica cu cat p are o valoare mai apropiata de 1,iar q o valoare mai apropiata de 0.

La inceputul procesului de departajare a variantelor comparate, discriminarea este hotarata de concordanta dintre variantele V_g si V_h definite prin relatia (VgPVh). Metoda arata ca daca in decursul procesului de departajare, concordanta nu reuseste sa clarifice raporturile de prioritate dintre variante, se apeleaza la contributia in aceasta directie a discordantei, majorand q pana spre valoarea q=1, cand discordanta, definita prin relatia (VgPVh), hotaraste ierarhizarea variantelor.

1.3 Metoda Onicescu

Metoda permite rationalizarea deciziilor multi criteriale in conditii de certitudine. Ea este conceputa de O. Onicescu, in doua versiuni:

a)      in versiunea 1, criteriile de alegere a variantei optime au aceeasi importanta. In acest caz, metoda comporta urmatoarele etape:

a.1) stabilirea matricei consecintelor alternativelor decizionale, notata cu A;

a.2) ordonarea variantelor pentru fiecare criteriu, in ordinea descrescatoare a consecintelor, obtinandu-se o noua matrice, notata cu B;

a.3) determinarea unei matrici c, in care se indica de cate ori o varianta i ocupa locul j. Aceasta matrice are urmatoarea forma:

Formula:

1 2 m

v₁ a₁₁ a₁₂ . . . a_1m

C= v₂ a₂₁ a₂₂ . . . a_2m

.

.

v_m a_m1 a_m2 . . .a_mm

In care _ij arata de cate ori varianta i ocupa locul j _ij Є 0,1,2,..,m;

a.4) ierarhizarea variantelor dupa o functie de agregare de forma:

f : V  R₊

definita prin formula:

Ierarhia variantelor decizionale se face pe baza valorilor descrescatoare ale acestei functii:

b)      in versiunea a II-a coeficientii de importanta atribuiti criteriilor sunt diferiti.

In acest caz, metoda comporta urmatoarele etape:

b.1) stabilirea matricelor A si B, intr-un mod identic cu cel din prima versiune;

b.2) atribuirea coeficientilor de importanta a criteriilor, dupa relatia:

in care: k =1 pentru criteriul cel mai important;

k =2 pentru criteriul considerat al doilea ca nivel de importanta, etc.

b.3) ierarhizarea variantelor dupa o functie de agregare de forma:

f : V  R₊

definita prin formula:

In care:  p = coeficientul de importanta al criteriului j

loc( V_I,C_J) = locul variantei i dupa criteriul j

Ierarhia variantelor decizionale se va face pe baza valorilor descrescatoare ale acestei functii.

. Metoda Topsis

In cazul metodei Topsis se cunosc preferintele cardinale asupra criteriilor.

Pas 1 se determina matricea consecintelor normalizate printr-o metoda de normalizare vectoriala,

Pas 2 se construieste matricea normalizata ponderata

  cu

Pas 3 se determina solutia ideala T*= ( t*₁, t*₂..t*_n) si solutia ideala negativa T^- = ( t₁^-, t₂^-..t_n^-), unde:

max t_ij , daca criteriul j este de maxim

^{1<i < m}

t^*_j=

min t_ij , daca criteriul j este de minim

^{1<i < m}

min t_ij , daca criteriul j este de maxim

^{1<i < m}

t ^-_j=

max t_ij , daca criteriul j este de minim

^{1<i < m}

Pas 4 se calculeaza distanta intre solutii (de obicei se considera distanta euclidiana)

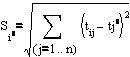si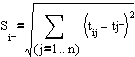

Pas 5 se calculeaza apropierea fata de solutia ideala

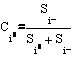
Pas 6 clasamentul optim este dat de valorile descrescatoare ale lui C_i^*

2 Optimizarea deciziilor in conditii de incertitudine

Incertitudinea reprezinta acea stare de cunoastere in care una sau mai multe alternative decurg dintr-o multime de rezultate posibile ale caror aparitii nu sunt cunoscute de catre decident. Acest lucru se intampla, de regula, atunci cand nu exista informatii disponibile din care sa poata fi calculate probabilitati obiective a posteriori si nici nu exista un mijloc pentru a determina probabilitati a priori. Prin urmare, intotdeauna, incertitudinea este subiectiva, ea fiind dependenta de perceptia decidentului.

Intrucat asteptarile decidentilor relative la mediul decizional sunt subiective, vor exista grade de incertitudine percepute diferit de catre acestia.

Procedura de luare a deciziei depinde de gradul de incertitudine perceput de decident. Doua sunt metodele principale utilizate in luarea deciziei in conditii de incertitudine:

Decidentul poate utiliza cea mai buna informatie disponibila si propria experienta si judecata pentru a identifica si asocia probabilitati subiective starilor posibile ale naturii si pentru a estima consecintele rezultate pentru fiecare strategie disponibila in fiecare stare data. Aceasta face, de fapt, conditia de incertitudine similara unei conditii de risc si procedurile de adoptare a deciziei prezentate in cazul conditiilor de risc sunt urmate si in cazul prezentei incertitudinii.

Daca gradul de incertitudine este atat de mare incat decidentul prefera sa nu faca ipoteze asupra probabilitatilor diferitelor stari ale naturii, el poate fie sa neglijeze probabilitatile, fie sa le considere ca fiind egale. Cand aceasta a doua metoda este aleasa, urmatoarele tehnici decizionale sunt disponibile pentru a evalua stategiile propuse:

a.       tehnica pesimista (Criteriul de decizie al lui Wald);

b.       tehnica optimista ( Criteriul maximax);

c.       tehnica proportionalitatii ( Criteriul Bayes-Laplace);

d.       tehnica minimizarii regretelor ( Criteriul decizional al lui Savage);

e.       tehnica de optimalitate (Criteriul Hurwicz).

2.1 Tehnica pesimista

Aceasta tehnica pleaca de la ideea ca varianta optima este acea varianta care presupune avantaje maxime in situatia in care conditiile obiective se prezinta cel mai nefavorabil.

Criteriul de decizie al lui Wald sau criteriul maximin, asa cum mai este cunoscuta in literatura de specialitate aceasta tehnica, este un criteriu conservator si o incercare de a maximiza nivelul de securitate al decidentului. El priveste natura ca actionand contrar intereselor sale. Altfel spus, criteriul recomanda sa se determine cel mai rau rezultat posibil al fiecarei variante decizionale si apoi sa se aleaga acea varianta care produce cel mai bun dintre aceste cele mai proaste rezultate.

Consideram o matrice decizionala ca in tabelul de mai jos:

Tabelul 4.4

unde: V_i = varianta decizionala

C_j = starea obiectiva

R_ij= consecinta decizionala aferenta variantei i si starii obiective j.

Decidentul va alege varianta decizionala optima, cu urmatoarea structura formalizata, care conduce la rezultatul:

V_optima=

V_optima reprezinta cea mai conservatoare strategie: ea include cel mai mic risc, dar si un rezultat asteptat mic. Deoarece criteriul este conservator si din punct de vedere financiar, el este preferat de catre firmele mici a caror supravietuire depinde de pierderile inregistrate.

2.2 Tehnica optimista

Aceasta tehnica are in vedere alegerea variantei optime in situatia in care conditiile obiective se prezinta cel mai favorabil. In acest caz decidentul este optimist in cel mai inalt grad si, ca urmare, alege rezultatul maxim al fiecariei variante. Ca atare:

V_optima=

Desigur ca o asemenea alegere este nerealista. Ea a fost inclusa pentru a arata faptul ca cele doua criterii, maximax si maximin reprezinta extremele criteriului alfa al lui Hurwicz, prezentat in continuare.

2.3 Tehnica de optimalitate

Bazata pe introducerea unui coeficient de optimism, utilizarea acestei tehnici necesita parcurgerea mai multor iteratii pentru obtinerea variantei optime, astfel:

● adoptarea coeficientului de optimism (0<α<1);

● determinarea elementelor H_i, dupa formula:

H_i = αA_i + (1-α) a_i

unde: A_i - elementul cel mai favorabil al liniei i ( variantei i)= max R_ij;

a_i - elementul cel mai nefavorabil al liniei i (variantei i)= min R_ij.

● alegerea variantei optime care corespunde variantei cu cel mai mare Hi.

V_optima = max H_i

Se observa ca coeficientul de optimism α ia valori intre 0 si 1, depinzand de atitudinea decidentului fata de risc. Daca decidentul este in totalitate pesimist, atunci α = 0. Rezultatul va fi atunci acelasi cu cel din cazul criteriului maxim. Daca decidentul este un optimist incurabil, atunci α = 1 si rezultatul va coincide cu cel dat de criteriul maximax.

De fapt, criteriul lui Hurwicz permite decidentului sa analizeze atat cel mai bun cat si cel mai slab rezultat al fiecarei variante decizionale si sa asocieze atat cel mai bun cat si cel mai slab rezultat al fiecarei variante decizionale si sa asocieze acestora o probabilitate subiectiva de aparitie. Evident ca, in acest caz, decizia adoptata depinde de valoarea lui α care la randul ei, depinde de atitudinea decidentului fata de risc. De regula, un astfel de criteriu se recomanda a fi utilizat in cadrul firmelor mijlocii cu mentiunea ca, daca gradul de optimism al decidentului este prea mare, sunt posibile pierderi insemnate de venit din partea firmei.

2.4 Tehnica proportionalitatii

Tehnica pleaca de la premisa ca fiecare stare a conditiilor obiective are aceeasi probabilitate de aparitie (starile conditiilor obiective sunt echiprobabile), iar varianta optima este aceea pentru care media aritmetica a rezultatelor corespunzatoare starilor luate in considerare este cea mai favorabila.

Matematic, formula de determinare a variantei optime este:

V_optima = * 1/n

unde: n - numarul starilor conditiilor obiective.

2.5 Tehnica minimizarii regretelor

Potrivit acestei tehnici, varianta optima este aceea pentru care regretul este minim. Regretul este masurat ca diferenta intre rezultatul unei variante decizionale date si rezultatul celei mai bune variante obtinut pentru aceeasi stare a naturii.

Motivatia utilizarii unei astfel de masuri a regretului este destul de simpla. Daca se produce oricare dintre starile naturii in viitor si noi am ales strategia care aduce castigul maxim pentru acea stare a naturii, atunci regretul este nul. Dar, daca alegem o alta strategie, regretul va fi dat de diferenta intre ceea ce am obtinut efectiv si ceea ce am fi putut castiga daca se adopta varianta decizionala optima in acea stare a naturii.

Iteratiile ce se parcurg in operationalizarea acestei tehnici au in vedere:

determinarea matricii regretelor, in care fiecare element se obtine scazand din valoarea sa initiala elementul maxim de pe coloana (matricea regretelor se obtine pe baza matricei decizionale):

r_ij = R_ij -  

determinarea valorilor maxime ale regretelor astfel obtinute, iar dintre acestea a valorii minime de pe fiecare linie (varianta):

V_optima =  

De observat ca decidentul care utilizeaza aceasta tehnica abandoneaza in mod explicit intentia de a maximiza rezultatul in favoarea unei variante prin care se obtine o valoare satisfacatoare a rezultatului cu un risc redus. De aceea, acest criteriu este utilizat mai ales in evaluarea unor proiecte investitionale cu o durata mare de desfasurare in timp.

Din prezentarea acestor tehnici de optimizare a deciziilor in conditii de incertitudine se sugereaza obtinerea unor variante optimale diferite. Se recomanda ca utilizarea uneia sau alteia din aceste tehnici sa aiba in vedere atat obisnuinta decidentului de a opera cu o anumita tehnica, psihologia managerului, cat mai ales situatia economico-financiara a firmei respective. Cu cat firma are o situatie economico-financiara mai buna, cu atat e posibila asumarea unor riscuri mai mari, deci viziuni mai optimiste asupra probabilitatilor de obtinere a unor rezultate superioare, pentru care exista resurse de compensare in caz de esec.

2.6 Metoda gradelor de apartenenta la varianta optima

In afara tehnicilor prezentate, pentru fundamentarea deciziilor in conditii de incertitudine se poate folosi si metoda gradelor de apartenenta la varianta optima. Aceasta metoda se poate folosi in conditiile impreciziei informatiilor necesare fundamentarii, sau a unei informari incomplete. Imprecizia poate fi determinata de caracterul probabilistic ale unor factori care influenteaza procesul decizional.

Metoda gradelor de apartenenta la varianta optima se bazeaza pe teoria multimilor vagi si necesita urmatoarele etape:

a)      formularea variantelor decizionale, a consecintelor acestora si alegerea criteriilor de optimizare. Consecintele variantelor, datorita informarii incomplete a decidentilor sau a impreciziei informatiilor se prezinta in termeni vagi (ex. Varianta 1 aduce un profit de cca. 10 milioane). Consecintele variantelor, dupa fiecare criteriu se prezinta intr-o matrice de forma:

a= a_ij

b)      pentru fiecare consecinta se efectueaza o transformare de variabila, dupa relatia:

₊

in care: a_ij -valoarea consecintei variantei, dupa criteriul j;

a⁺_j-valoarea consecintei optime dupa criteriul j.

c)      Stabilirea gradelor de apartenenta a fiecarei variante la varianta optima, pentru fiecare criteriu de decizie, dupa o functie exponentiala de forma:

in care:

k -coeficient de apartenenta, acesta luand valori in functie de importanta criteriilor de optimizare. Astfel, pentru criteriile mai putin importante, k ia valori mici, iar pentru criteriile mai importante k ia valori mai mari. Literatura de specialitate recomanda pentru k valori cuprinse intre 3 si 6. Valorile _ij se inscriu intr-o matrice ale carei elemente evidentiaza gradul de apartenenta a fiecarei variante decizionale la varianta optima, pentru fiecare criteriu de optimizare.

d)      alegerea variantei optime, prin agregarea elementelor matricei gradelor de apartenenta la varianta optima, dupa una dintre regulile de optimizare a deciziilor in conditii de incertitudine, prezentate anterior. Spre exemplu, folosind regula Laplace, valoarea medie a unei variante se poate calcula cu relatia:

Se considera varianta optima cea pentru care valoarea medie este cea mai mare.

3 Optimizarea deciziilor in conditii de risc

In natura si in viata au loc diferite evenimente, unele dorite sau favorabile, altele nefavorabile. In teoria statistica si economica, evenimentele sunt adesea numite stari ale naturii si aceasta deoarece ele nu sunt controlabile de catre om. In activitatea sa, omul insa le poate evita; poate alege cai cu evenimente ce minimizeaza pericolele. Astfel, el minimizeaza riscul la care se poate expune, fara a le elimina complet, daca fenomenele raman aleatoare. Oamenii au capacitati de risc diferite, functie de caracteristicile lor biologice si de puterea lor economica.

Omul nu poate elimina complet riscul in cazul cand au loc fenomene aleatoare. Sta insa in puterea lui reducerea riscului pana la un nivel minim care sa-l faca acceptabil. Pentru aceasta se procedeaza la o analiza probabilistica de evaluare si selectie decizionala.

Metodele cantitative cel mai des intrebuintate in acest sens sunt speranta matematica a rezultatelor si arborii de decizie.

Metoda sperantei matematice

Speranta matematica a rezultatelor unor actiuni economice este marimea medie ponderata a rezultatelor activitatii, ponderile fiind egale cu probabilitatile evenimentelor sau starilor naturii.

Astfel, daca in cazul unei variante V_i de rezolvare a unei probleme, caracterizate de fenomene aleatoare, reprezentate prin x_j, probabilitatile producerii lor p(x_j) si rezultatele ce se obtin r_ij, atunci speranta matematica a rezultatelor in varianta V_i, notata cu E(V_i), va fi data de relatia :

___

E (V_i) = r_ij p(x_j); i = 1,m; 0 < p(x_j) < 1; p(x_j) = 1

Daca rezultatele r_ij sunt exprimate prin efecte economice cum sunt profitul, incasarile din vanzari , dividendele, productivitatea, s.a., atunci varianta optima, sau decizia optima de rezolvare a problemei, va fi cea care satisface conditia:

max E(V_i) => V_i^*

i

iar daca rezultatele r_ij exprima eforturi ca, de exemplu, investitii, costuri de exploatare, consumuri specifice, s.a., varianta optima va fi obtinuta din conditia minimizarii riscului:

min E(V_i) => V_i^*

i

Metoda arborelui decizional

In conditiile unei situatii decizionale complexe, in care momentele de

decizie alterneaza cu momentele aleatoare, decidentul poate utiliza, ca instrument practic de rationalizare a deciziilor in conditii de risc, arborele decizional.

Esentialmente, numele de arbore decizional vine de la asemanarea reprezentarii sale grafice cu un arbore stilizat (fig. 4.2), desenat orizontal. Este o metoda de analiza a rezultatelor potentiale ale unei decizii complexe, utilizata in procesul decizional strategic din cadrul firmelor.

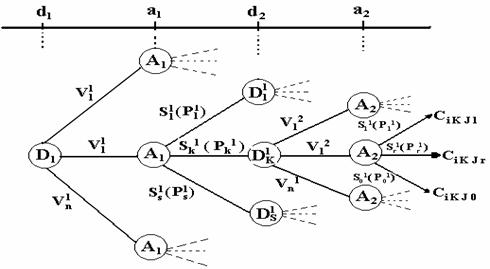
Arborele decizional poate fi utilizat pentru situatii decizionale strategice complexe, din cadrul societatii comerciale sau regiei autonome,

Fig. 4.2. Arborele decizional

comportand o serie de decizii, probabilitatea de producere si dimensiunile fiecarei dintre ele fiind determinate de decizia luata in faza precedenta.Fiecare decizie depinde de rezultatul unui eveniment aleatoriu, care insa nu poate fi determinat in momentul luarii ei, dar a carui probabilitate poate fi anticipata in urma investigatiilor facute.

In figura de mai sus , s-au utilizat urmatoarele simboluri:

D- noduri decizionale

d - momente decizionale

a - momente aleatoare

A- noduri aleatoare

C- consecinte

Spre exemplu, C_ik_jr reprezinta consecinta variantei (i) din momentul decizional (d₁), in starea conditiilor obiective (k) din momentul aleator (a₁), a variantei(j) din momentul decizional (d₂) in starea conditiilor obiective(r) de momentul aleator (a₂).

Solutionarea problemei decizionale se va face pornind de la cerintele fiecarei variante, potrivit conceptului "roll back", prin calculul sperantei matematice.Astfel, pentru modului decizional, D¹_K :

(C_ikj1 x P¹₁) + (C_ikjr x P¹_r) + (C_ikj0 x P¹₀) = Spj

unde : Spj - speranta matematica a variantei j din momentul decizional d₂

In acest fel se va proceda pentru toate variantele, alegandu-se cea pentru care speranta matematica este maxima. In continuare se va proceda la fel si in celelalte noduri decizionale din momentul decizional d₂. In final , se vor obtine sperante matematice maxime din fiecare nod decizional din momentul d₂, cu care se va continua pentru stabilirea variantei optime in nodul decizional D₁, din momentul decizional d₁, dupa aceeasi procedura. Varianta optima in nodul decizional D₁ va fi cea pentru care speranta matematica este maxima.

Aplicarea metodei arborelui decizional la situatiile decizionale complexe presupune parcurgerea mai multor etape, intre care:

- stabilirea momentelor aleatoare si a celor de decizie, precum si a alternantei lor ;

- culegerea informatiilor referitoare la alternativele posibile;

- reprezentarea arborelui decizional si stabilirea probabilitatilor de manifestare a starilor conditiilor obiective;

- calculul sperantei matematice, incepand cu ultimele noduri decizionale si continuand pana la nodul decizional initial.

Arborele decizional s-a dovedit un instrument deosebit de util in solutionarea unor probleme decizionale cu complexitate mare din cadrul firmelor.

4 Optimizarea deciziilor de grup

4.1 Algoritmul Deutch-Martin

Potrivit acestui algoritm se considera o ordine oarecare a variantelor:

Tabelul 4.5

Etapele metodei sunt:

Determinarea momentelor linie dupa relatia:

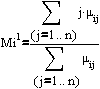
In care: M_i¹reprezinta momentul linie (I);

U_ij utilitatea variantei (I) dupa decidentul (j);

n-numarul decidentilor;

j-numarul de ordine al decidentului.

Se ordoneaza liniile in ordinea crescatoare a momentelor linie.

Determinarea momentelor coloana dupa relatia:

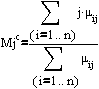
In care: M^c_j-momentul coloana;

I este numarul de ordine al variantei (I);

Se ordoneaza coloanele in ordinea crescatoare a momentelor coloana.

Se repeta calculele momentelor linie si momentelor coloana pana cand nu mai sunt posibile ordonari. In acest caz, ordinea stabilita este cea optima.

4.2 Metoda Electre Tridimensionala

Aceasta metoda se foloseste pentru optimizarea deciziilor multicriteriale de grup, in care decidentii au preferinte diferite asupra utilitatii variantelor.

Etape:

a)      stabilirea de catre fiecare decident, a utilitatii fiecarei variante, pentru fiecare criteriu. Utilitatea variantelor se stabileste ca in metoda utilitatii globale.

b)      determinarea indicatorilor de concordanta ai variantelor se face dupa formula:

unde :

se face pentru acei j pentru care toti decidentii apreciaza ca u_gj≥u_hj

c)      determinarea indicatorilor de discordanta ai variantelor:

pentru acei j pentru care toti decidentii apreciaza ca u_gj≤u_hj

d)      alegerea variantei optime pe baza relatiei de surclasare a variantelor. Pentru alegerea variantei optime se procedeaza ca in metoda Electre clasica.

4.3. Calculul majoritatii ca o compunere de utilitati individuale

Unii specialisti abordeaza deciziile de grup ca o compunere de utilitati individuale. Diferentele intre decidenti prin prisma utilitatilor apar ca urmare a aprecierii diferite din partea acestora a importantei criteriilor decizionale folosite in fundamentarea deciziei de grup. Evident ca aceste utlitati individuale (apreciate de catre fiecare component al grupului decident) pot fi aceleasi sau pot fi diferite. Variantele decizionale se vor ierarhiza prin prisma acestor utilitati.

Pentru exemplificare consideram o situatie decizionala in care (n) decidenti trebuie sa aleaga dintre (m) variante una care sa reprezinte optiunea reprezentativa pentru grup, situatie ce poate fi sintetizata in tabelul 4.6

Tabelul nr.4.6

Utilitatea fiecarei variante se calculeaza dupa metoda utilitatii globale, asa cum se poate observa din ultima coloana a tabelului 4.6. Utilitatea globala maxima va desemna varianta optima.