PROGRAMAREA ACTIVITATILOR. GRAFICE GANTT.

1. Grafice Gantt

In acest subcapitol se exemplifica modul de reprezentare a proiectelor prin modele intuitive, grafice, bazate mai ales pe teoria grafurilor. In literatura de specialitate exemplele sunt numeroase ([1]). Modelarea matematica a proiectelor permite managerului de proiect luarea unor decizii importante, mai ales in domeniul optimizarilor de resurse (cost/durata).

Diagramele sau graficele Gantt - numite astfel dupa autorul lor - sunt reprezentari ale activitatilor proiectului prin "bare" de-a lungul axei timpului. Lungimea fiecarei bare este proportionala cu durata activitatii reprezentate. Diagramele Gantt se mai numesc si diagrame cu bare ("bar-chart").

Desi diagramele Gantt au fost utilizate cu mult timp inaintea aparitiei metodelor de modelare a proiectelor cu ajutorul grafurilor, calitatile lor complementare fac sa fie utilizate impreuna cu acestea in mod absolut firesc.

Sunt insa numeroase si situatiile/aplicatiile in care diagramele Gantt se folosesc in mod independent.

2. Modelul determinist CPM

Deoarece un proiect este, in esenta, un set de activitati, cu momente determinate de incepere si de finalizare, intre care exista relatii de interdependenta bine precizate, multimea activitatilor proiectului poate fi reprezentata de un graf.

Graful este o multime de arce si noduri, astfel incat reprezentarea unui proiect se poate face in doua moduri, in functie de conventia de reprezentare:

"activitate = arc";

"activitate = nod".

Metoda CPM (Critical Path Method = Metoda "drumului critic") porneste tocmai de la o astfel de conventie de reprezentare. "Drumul critic" este submultimea de arce si noduri ale grafului (numite, si ele, "critice") care unesc momentele initial si final ale proiectului, astfel incat lungimea drumului critic (suma duratelor activitatilor critice) reprezinta durata minima de realizare a intregului proiect.

Exemplu de aplicare a Metodei CPM pe baza conventiei de reprezentare "activitate = arc"

In tabelul 1 se prezinta, cu titlu de exemplu, un model de proiect - evident simplificat - precum si etapele de calcul in aplicarea metodei CPM. Am evitat prezentarea formulelor si calculelor pentru ca aceasta ar consuma relativ mult spatiu in economia lucrarii dar si pentru motivul ca exista suficient de multe materiale pe aceasta tema.

Pe de alta parte, exista programe, aplicatii informatice de firma (Microsoft, Primavera) care rezolva aplicatiile practice de mari dimensiuni.

Tabelul 1

Activitatile proiectului si duratele asociate

3. Modelul probabilist PERT

Metoda PERT (Programme Evaluation and Review Technique = Evaluarea programelor si tehnica revizuirii lor) se refera atat la programe cat si la proiecte. Metoda se deosebeste de CPM prin faptul ca proiectele modelate sunt de natura probabilista si, ca urmare, nu au durate certe. In aceste conditii, pentru fiecare activitate (i, j) se pot estima, de catre experti, trei durate:

durata optimista (cea mai scurta) - fie ea a_ij;

durata pesimista (cea mai lunga) - fie ea b_ij;

durata cea mai probabila - fie ea m_ij.

Se calculeaza, pentru fiecare activitate, durata medie:

si dispersia (abaterea medie patratica):

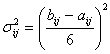
Se determina drumul critic la fel ca in CPM, locul duratei deterministe d_ij fiind insa luat de durata medie d_ij.

In plus, este necesar si posibil sa se estimeze probabilitatea de realizare a proiectului la termenul impus (T_P). Cunoscand valoarea drumului critic (T_C) si dispersia intregului proiect (s, calculata ca suma a dispersiilor activitatilor critice) se determina parametrul z:

In tabelul 2 se gaseste corespondenta cautata P (T_C < T_P) = j (z). De exemplu, pentru z = 0 se gaseste j .

Tabelul 2

Valorile functiei φ (z)