Concepte si erori in testarea ipotezelor statistice

1. Revizuirea termenilor elementari

Obtinerea datelor necesare analizei statistice si construirii modelelor econometrice se realizeaza prin urmatoarele forme de observare:

- observare exhaustiva: cand inregistrarea caracteristicilor urmarite prin programul de cercetare se realizeaza pentru toate unitatile populatiei;

- observare partiala cand inregistrarea caracteristicilor urmarite prin programul de cercetare se realizeaza numai pentru o parte a unitatilor populatiei.

Sondajul statistic este cercetarea partiala in urma careia, pe baza rezultatelor obtinute prin prelucrarea datelor din esantion se estimeaza, folosind principiile teoriei probabilitatilor, parametrii corespunzatori ai populatiei totale.

In aceasta definitie intalnim doua concepte fundamentale: populatie si esantion.

Populatia reprezinta totalitatea unitatilor simple sau complexe care formeaza obiectul cercetarii prin sondaj. Orice cercetare trebuie sa inceapa cu delimitarea in timp si spatiu a populatiei. Notiunea de populatie trebuie privita avand in vedere intelesul statistic al notiunii si anume multimea unitatilor pe care le are in vedere cercetarea.

Studierea unei populatii presupune inregistrarea mai multor valori pentru fiecare unitate individuala. De exemplu daca populatia este formata din totalitatea angajatilor unei companii vom putea inregistra valori cu privire la: venit, varsta, scorul obtinut la un test de aptitudine, sex sau nivelul studiilor. Fiecare set de valori se concretizeaza intr-o variabila aleatoare.

Esantionul este format din unitatile simple sau complexe pentru care se inregistreaza caracteristicile in conformitate cu obiectivele propuse.

Scopul urmarit prin extragerea unui esantion dintr-o populatie este ca valorile obtinute in urma prelucrarii datelor din esantion sa poata fi generalizate asupra intregii populatii. Sondajul presupune deci doua faze distincte:

Faza I: Observare si descriere statistica. Aceasta consta in extragerea esantionului si calcularea valorilor ce definesc caracteristicile studiate: medii, dispersii, coeficienti de variatie, asimetrie, etc.;

Faza II: Inferenta statistica. Aceasta consta in extinderea indicatorilor esantionului asupra populatiei. Aceasta operatie poarta denumirea de estimare.

Pe parcursul celor doua faze vom intalnii indicatori ai esantionului si indicatori ai populatiei totale. Primii sunt valori de sondaj si se numesc estimatori iar ceilalti parametrii.

Exista mai multe sisteme de notatii pentru cele doua seturi de indicatori. In acest curs vom folosi urmatoarele notatii:

Modul in care vom calcula parametrii si estimatorii depinde de natura variabilei aleatoare. Acestea pot fi cantitative (venit, varsta sau scorul obtinut la testul de aptitudini) sau calitative (sex sau nivelul studiilor).

Variabilele cantitative pot fi discrete sau continue. Variabilele numarabile, ca de exemplu numarul de copii sau numarul de accidente de munca, sunt in mod uzual discrete. Continue sunt acele variabile care pot lua orice valoare reala (inclusiv valori fractionle) intr-un interval dat.

O alta diferentiere a variabilelor cantitative si calitative este realizata cu ajutorul scalei pe care acestea sunt masurate.

In domeniul stiintelor economico-sociale se intalnesc urmatoarele tipuri de scale:nominala, ordinala, de interval si proportionala.

Scala nominala Aceasta este cea mai rudimentara. Fiecare termen are aceeasi importanta, aceeasi greutate. O asemenea scala nu constituie decat o enumerare de posibilitati. Este un tip de scala neparametrica care permite clasificarea unitatilor studiate in doua sau mai multe grupe ai caror membrii difera dupa proprietatea ce a fost scalata, fara sa duca si la realizarea unei ordonari

Scala ordinala. Aceasta permite o oarecare clasificare a opiniilor. Ofera posibilitatea nu numai de a marca deosebiri ci si de a stabili pozitii inferioare si superioare.   

Scala de intervale (cardinala). In aceasta scala nu numai ca se situeaza pe diferite trepte pozitiile celor chestionati dar se si poate calcula distanta dintre diferitele trepte . Exemplu: numerotarea cronologica.

Scala proportionala. Are toate caracteristicile scalei de interval si in plus punctul zero al scalei este dat in mod natural fapt ce permite efectuarea tuturor calculelor cerute de logica analizei. Este folosita pentru masurarea valorilor variabilelor: inaltime, greutate, distanta, pret, viteza, etc.

In practica aplicarii stiintelor sociale intalnim cel mai des scale nominale si ordinale apeland rareori la scalele de ordin superior (doar pentru variabile numerice).

Tabel nr. 1

Manipularea datelor sub SPSS (versiunea 13)

Revolutia tehnica si tehnologica aduce numeroase avantaje si face posibila tratarea unui volum mai mare de informatii intr-un mod mult mai rapid si mult mai putin costisitor. Aparitia informaticii este foarte importanta deoarece permite prelucrarea rapida a datelor si aplicarea cu usurinta a metodelor avansate de analiza statistica si econometrie.

Din acest motiv, la majoritatea capitolelor aplicatiile sunt insotite si de explicatii pentru rezolvarea acestora in SPSS. Deoarece primul pas in analiza statistico-econometrica sub un soft specializat il reprezinta introducerea datelor si definirea variabilelor, in acest subcapitol vom trata aceste aspecte.

Prelucrarea datelor sub SPSS presupune familiarizarea cu doua ferestre de lucru: fereastra de definire si vizualizare a variabilelor -Variable View (figura 1) si fereastra de introducere si vizualizare a bazei de date - Data View ..

Figura 1 Fereastra de definire si vizualizare a variabilelor

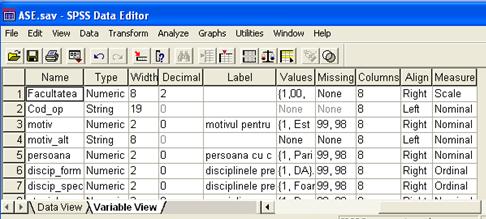
Variabilele ce stau la baza analizei statistice si econometrice pot fi primare (obtinute in urma centralizarii si codificarii datelor dintr-o observare totala sau selectiva) sau derivate (construite pe baza celor primare in urma recodificarii sau aplicarii unor relatii de calcul asupra acestora).

Indiferent de tipul variabilelor este acestea trebuie sa fie definite cu ajutorul capului de tabel din fereastra Variable View astfel:

Name. Se introduce numele variabilei. Acesta trebuie sa fie unic, nefiind posibila adresarea a doua sau mai multe variabile cu acelasi nume.

Type. Se refera la definirea tipului de data ce urmeaza sa fie introdusa. Acesta poate fi:

• Numeric. Valorile introduse sunt numere afisate in format numeric standard. Este optiunea implicita.    Atentie, valorile introduse sunt numerice ceea ce nu inseamna ca neaparat variabila pe care o definim este cantitativa. Avem variabile cantitative pe care le vom codifica pentru a usura prelucrarea. In aceasta situatie numerele afisate sunt codurile asociate.
• Comma. O valoare numerica ce foloseste virgula pentru a delimita perioade de trei pozitii;
• Dot. O valoare numerica ce foloseste punctul pentru a delimita perioade de trei pozitii;
• Scientific notation. O valoare numerica ce este afisata in format stiintific (123E+2);
• Date. O valoare numerica care    reprezinta o data calendaristica sau moment de timp exprimat in ore/minute/secunde;
• Dolar. O valoare numerica precedata de semnul monetar $.
• Custom currency. O valoare numerica ce este afisata in unul din formatele definite de utilizator in fereastra obtinuta din Edit/ Options/Currency;
• String. Variabila alfanumerica.

With. Lungimea exprimata in numarul maxim de caractere acceptate.

Decimals. Numarul de zecimale cu care se afiseaza valoarea numerica;

Label. Eticheta variabilei. Nu este un camp obligatoriu dar este deosebit de util atunci cand dorim ca in tabelele si graficele rezultate in urma analizei sa avem o definire explicita a variabilei si nu una prescurtata precum numele variabilei.

Figura 2 Exemplu de definire a campului Values

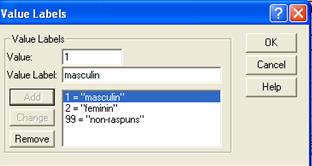
Values. Nu este camp obligatoriu. Aici putem defini valorile (asociate codurilor) pe care vrem sa le vedem in tabelele si graficele rezultate in urma prelucrarii. In figura nr. 2 este prezentat modul in care se definesc valorile codificate.

Missing. Nu este camp obligatoriu. In mod conventional raspunsurile de genul "nu stiu" sau non-raspunsul sunt codificate cu 98 respectiv 99. Deoarece nu dorim ca aceste valori sa fie luate in consideratie in calculul estimatorilor este important sa le definim ca valori lipsa.

Columns. Reprezinta marimea coloanei pe care o va avea variabila definita in baza de date.

Align. In baza de date valorile variabilei pot fi aliniate la stanga, dreapta sau centru.

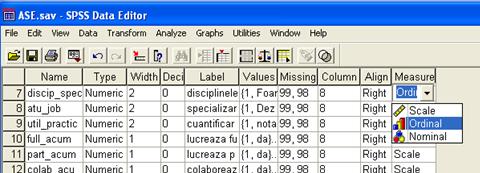
Measure. Reprezinta scala pe care este masurata variabila (figura 3). Este foarte important ca aceasta sa fie corect definita deoarece metodele de analiza utilizate depind de tipul variabilei (vezi tabelul 1).

Figura 3 Alegerea scalei

Uneori, in urma examinarii bazei de date de care dispunem putem constata ca este necesar sa cream noi variabile derivate, pe baza valorilor uneia sau mai multor variabile deja existente.

Variabilele derivate pot fi obtinute cu ajutorul urmatoarelor comenzi din meniul Transform:

Compute. Permite crearea unei noi variabile in urma aplicarii unor relatii de calcul intre una sau mai multe variabile.

Recode. Permite recodificarea unei variabile fie prin modificarea celei existente fie prin crearea unei variabile derivate.

Count. Creeaza o noua variabila contorizand numarul de aparitii al unei valori sau a unui set de valori in una sau mai multe variabile.

3. Procedee de baza utilizate in testarea ipotezelor

In toate domeniile stiintelor aplicate este necesar sa se recurga la experimentarea unor noi metode, tehnologii, produse, facandu-se presupuneri asupra superioritatii lor fata de procedeele curent folosite in vederea luarii unei anumite decizii. Totodata este necesar sa verificam daca in timp s-au produs modificari in ceea ce priveste parametrii populatiei sau exista diferente semnificative intre diferite grupuri ale aceleiasi populatii. Toate aceste presupuneri constituie niste ipoteze a caror valabilitate trebuie verificata si deoarece aceasta verificare se face statistic (operandu-se cu date obtinute in urma unei selectii statistice dintr-o populatie) ele se denumesc ipoteze statistice.

Verificarea concordantei rezultatelor experientei cu una dintre ipoteze se face pe baza unui criteriu statistic furnizat de un ansamblu de reguli de prelucrare a datelor numit test statistic. Cu ajutorul lui se ajunge la decizia de a respinge o ipoteza si a accepta alta. Luarea unei decizii cu privire la o ipoteza statistica se numeste testarea ipotezei.

Fie o variabila aleatore X, considerata pe o populatie a carei functie de repartitie este specificata dar care depinde de un parametru necunoscut q. Ipoteza conform careia q are valoarea q se noteaza H₀: q = q si poarta numele de ipoteza nula. Sa presupunem ca in afara valorii q mai poate avea si valorile q_1, q₂ ,q_3, . Ipotezele H_i: q = q_i se numesc ipoteze alternative ale ipotezei nule.

O ipoteza se numeste simpla daca ea determina in mod univoc repartitia specificata a variabilei aleatoare si compusa daca este formata dintr-un numar finit de ipoteze simple.

Testele statistice furnizeaza criterii pe baza carora se accepta sau se respinge o ipoteza cu privire la o populatie statistica pe baza observatiilor facute intr-un esantion aleator extras din ea.

Alegerea testului nu depinde de esantion, de aceea procedeul de testare a ipotezei si ipoteza se pot specifica inainte de selectie.

Trebuie subliniat faptul ca printr-un test statistic nu se stabileste adevarul ci doar daca rezultatele selectiei sprijina ipoteza formulata si cu ce probabilitate.

Pentru construirea unui test statistic, principiul consta in impartirea spatiului de selectie X intr-o regiune critica reprezentata de submultimea W si o regiune de acceptare reprezentata de submultimea w.

Ipoteza statistica avansata se accepta daca vectorul de selectie x apartine submultimii w si se respinge daca apartine submultimii W.

Pentru transpunerea in practica a acestui principiu testul statistic presupune:

o statistica a testului, adica o variabila aleatoare functie de valorile din esantion la care se ajunge printr-o modalitate de prelucrare proprie fiecarui test;

un criteriu de decizie asupra ipotezei cu care sa se compare valoarea calculata a statisticii testului.

Fie: x=( x₁, x₂, ., x_n) vectorul aleator de selectie obtinut din spatiul de selectie X, T=f(x₁, x₂, ., x_n) statistica testului, V submultimea valorilor statisticii T pentru care ipoteza avansata se respinge si v submultimea valorilor statisticii T pentru care ipoteza se accepta. Submultimii V a statisticii testului ii corespunde in spatiul de selectie submultimea W, iar submultimii v a testului ii corespunde in spatiul de selectie submultimea w.

Exista o valoare T_c a statisticii testului care delimiteaza valorile posibile in regiunea critica V si regiunea de acceptare v. Aceasta valoare T_d este criteriul de decizie asupra ipotezei. Ea este tabelata in functie de volumul probei si de probabilitatea de cuprindere a valorilor lui T in regiunea critica V.

Odata cu formularea ipotezei si cu alegerea unui test adecvat se stabileste si probabilitatea de cuprindere a valorilor in regiunea critica. O ipoteza este respinsa cand T V pentru ca implicit xW si se accepta cand Tv pentru ca xw.

Indicatorii obtinuti pe baza datelor din sondaj se vor utiliza pentru estimarea parametrilor din populatie dupa ce in prealabil s-a verificat stabilitatea lor. Aceasta extindere tine de inferenta statistica deoarece, informatiile obtinute pe baza esantioanelor sunt utilizate pentru a formula concluzii asupra populatiilor din care acestea provin. In vederea garantarii acestei "credibilitati", pentru verificarea ipotezelor se utilizeaza diferite teste statistice pentru:

A. Verificarea parametrilor repartitiilor. Acestea se utilizeaza pentru a compara estimatorii obtinuti prelucrand datele din esantion cu parametrii corespunzatori ai populatiei sau pentru compararea estimatorilor proveniti din esantioane diferite.

B. Testarea concordantei repartitiilor. "In urma efectuarii unui sondaj se formuleaza o anumita ipoteza cu privire la legea de repartitie pe care o urmeaza caracteristicile studiate."[1] Aceste teste statistice se utilizeaza pentru a verifica daca valorile inregistrate urmeaza intr-adevar repartitia teoretica presupusa.

Verificarea ipotezelor statistice presupune respectarea unui algoritm in cinci pasi.

Pasul 1. Verificarea premizelor.

Orice aplicare a unor metode statistico-econometrice porneste de la anumite premize ce trebuie respectate de setul de date. Acestea se refera la: conditiile in care au fost selectate esantioanele, marimea esantioanelor, tipul variabilelor, forma distributiilor esantioanelor si dispersiile acestora.

Pasul Stabilirea ipotezei nule (H₀).

Aceasta este elementul central al oricarui test statistic deoarece intreaga procedura se rezuma la acceptarea sau respingerea acesteia. Reprezinta situatia inexistentei diferentelor semnificative intre parametrii testati sau intre formele repartitiilor.

In mod uzual, cercetatorul considera ca exista diferente semnificative statistic dorind sa respinga ipoteza nula in favoarea celei alternative denumita si ipoteza cercetata (H₁). Aceasta reprezinta o teorie care contrazice in totalitate ipoteza nula.

Pasul 3. Alegerea testului statistic potrivit si stabilirea regiunii critice.

Alegerea testului se face pornind de la premizele formulate la pasul 1 si in conditiile ipotezelor formulate la pasul Regiunea critica se stabileste pornind de la valoarea T_c acesta fiind punctul de taietura ce separa regiunea critica de regiunea de acceptare. Este o valoare tabelata in functie forma distributiei, de volumul probei si de probabilitatea cu care se garanteaza rezultatele.

Pasul 4. Calcularea valorii testului conform statisticii acestuia.

Valoarea obtinuta se numeste "valoarea calculata a testului".

Pasul 5. Luarea deciziei.

Este ultimul pas in procesul de verificare a ipotezelor statistice. Daca valoarea calculata a testului apartine regiunii critice decizia va fi de respingere a ipotezei nule. Daca valoarea calculata nu apartine regiunii critice se accepta ipoteza nula si se respinge alternativa.

Acest algoritm in cinci pasi poate fi utilizat ca model in procedeul de verificare a oricarei ipoteze statistice.

4. Tipuri de erori intalnite in testarea ipotezelor

La admiterea sau respingerea unei ipoteze statistice se pot face doua tipuri de erori.

Respingerea ipotezei H₀ cand aceasta este adevarata se numeste eroare de tip I. Probabilitatea unei asemenea erori se noteaza cu α.

Deci, P=α sau: P=α

Acceptarea ipotezei H₀ cand de fapt este falsa sau respingerea ipotezei alternative cand este adevarata se numeste eroare de tipul II si are o probabilitate β. Eroarea de tipul II este dependenta de alegerea nivelului de semnificatie α si de ipoteza H_A formulata.

P=P=β sau:

P=β sau P=β

Din aceste relatii rezulta ca: P = 1-α si

P=1-β

Daca se accepta un nivel de semnificatie α de 0,05 sau 5% inseamna ca H₀ se accepta in 95% din cazuri si se respinge in 5% din ele.

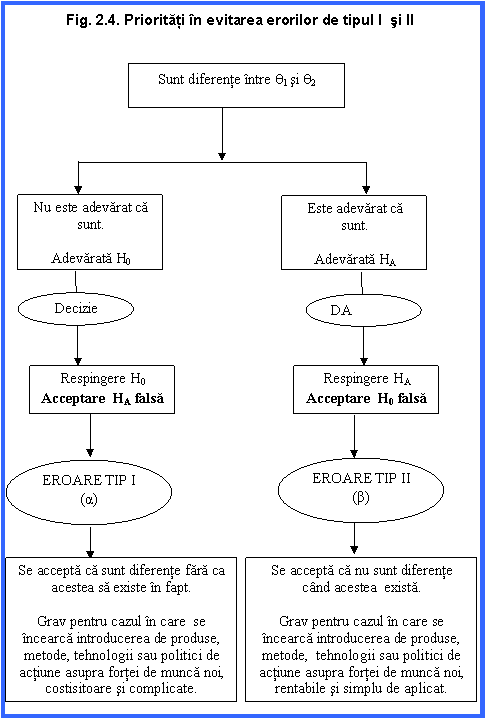
In oricare testare de ipoteza numai una din cele doua greseli se poate face dar nu se poate preciza care anume. Legatura dintre cele doua tipuri de erori reiese clar din urmatorul rationament: reducerea lui α sporeste acceptanta lui H₀ si uneori s-ar putea accepta si fara sa fie adevarata ceea ce inseamna marirea lui β .

Erorile de tip I pot fi micsorate de cercetator fixand nivelul de semnificatie α cat mai mic. Erorile de tip II pot fi micsorate prin cresterea volumului esantionului. Daca variatia selectiei este mai mica se reduc ambele erori.

"Deoarece evitarea unui tip de eroare sporeste sansa celeilalte devine important de stiut care tip de eroare trebuie mai atent evitat."

Raspunsul nu este unic ci depinde de obiectivele cercetarii (fig. 4). Daca se testeaza promovarea unor solutii mai scumpe sau mai complicate este de dorit sa nu fie insotite de erori mari de tipul I.

Prin functia de putere a unui test statistic, notata cu Π(W,θ) se intelege probabilitatea respingerii ipotezei H₀ in functie de θ. Respingerea ipotezei H₀ se face atunci cand vectorul de selectie x apartine submultimii W a spatiului de selectie si se poate scrie:

Π(W,θ)= P

Dupa cum este adevarata ipoteza H₀: θ= θ₀ sau H_A: θ= θ₁ , se poate calcula puterea testului fata de fiecare ipoteza:

Π(W,θ₀)= α sau Π(W,θ₁)=1-β

Aceasta relatie defineste puterea testului ipotezei H₀ . Ea este cu atat mai mare cu cat riscul de tipul II este mai mic.

Problema fundamentala in teoria verificarii ipotezelor statistice este de a alege dintre toate testele avand acelasi prag de semnificatie α acela pentru care puterea este maxima (β este minim). Acel test se numeste cel mai puternic test si poate fi construit pentru o clasa de repartitii.