JOCURI NECOOPERATIVE SI PROBLEMA ECHILIBRULUI

JOCURI NECOOPERATIVE SI PROBLEMA ECHILIBRULUI

1. Jocuri necooperative

Intr-o acceptiune larga prin joc de m decidenti ( jucatori ) se intelege ansamblul ,

unde:

reprezinta multimea decidentilor

este o multime nevida numita multimea strategiilor (simple) ale decidentilor

Vom nota

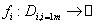este functia de utilitate a decidentului i

Conceptul de joc exprima in esenta un model matematic de analiza a situatiilor conflictuale-competitionale.

Caracterul conflictual al situatiei decizionale deriva din faptul ca obiectivele decidentilor nu pot fi realizate simultan, iar acte individuale in lipsa schimbului de informatii si acorduri ferme.

Primele lucrari consacrate studiului elementelor de baza ale teoriei jocurilor se datoreaza lui Neumann si au avut ca punct de plecare studiul unor fenomene de piata. Ulterior rezultatele obtinute au fost extinse prin contributia unor matematicieni si economisti de mare valoare ( Morgestern, Nikaide, Karlin etc.); s-au pus astfel bazele unei noi teorii matematice cu implicatiimajore in rezolvarea unor probleme tehnico-economice extrem de importante:

probleme de analiza sigurantei in functionare a sistemelor fizice;

probleme de analiza si previziune economica;

probleme de cooperare, etc.

1.1.Strategii si valori optime garantate

Sa consideram pentru inceput jocul cu doi decidenti:

Definitia 1

Marimile

(1)

(2)

reprezinta valorile optime garantate ale celor doi decidenti.

In cazul in care marginile din (1) si (2) sunt atinse atunci strategiile pentru care se

ating aceste margini se numesc strategii optime garantate.

Un caz important al jocurilor necooperative il constituie acela cand . Acest tip de joc se numeste joc cu suma nula.

Observatia 1

Semnficatiile strategiilor si a valorilor optime garantate in contextul jocurilor necooperative este urmatoarea:

Daca este strategic optima garantata a primului decident, atunci marimea:

reprezinta castigul maxim sigur pe care-l poare obtine primul decident;

Daca este strategia optima garantata a celui de-al doilea decident, atunci marimea:

reprezinta pierderea maxima la care se poate astepta cel de-al doilea decident.

1. Jocuri matriciale

Fie jocul cu suma nula (deci ) in care multimea de strategii sunt finite

,

Se noteaza ,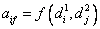

Se observa ca jocului i se poate pune in evidenta matricea .Din acest motiv aceste jocuri sunt cunoscute sub numele de jocuri matriciale.

Definitia 2

Fie jocul matricial , ,

Se numesc strategii mixte ale decidentilor 1 si 2 orice reparatii de probabilitati pe multimile .

Observatia 2

Fie ,

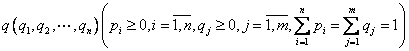
Doua strategii mixte ale decidentilor.

Aceasta inseamna ca decidentul 1 va folosi strategic cu probabilitatea , iar decidentul 2 va utiliza strategia cu probabilitatea .

Observatia 3

Ultima teorema ne arata ca orice joc matricial are punct sa in strategii mixte.

Observatia 4

Exista posibilitatea ca un joc matricial sa nu aiba totdeauna puncte sa in strategii simple. De exemplu, daca vom considera un joc matricial descris de matricea urmatoare:

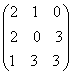
se poate constata imediat ca:

Din acest motiv se impune gasirea unor metode care sa permita rezolvarea jocurilor matriciale in strategii mixte.

Pentru inceput vom considera urmatorul rezultat:

Teorema 1

Au loc rezultatele urmatoare:

intr-un joc matricial 2 x 2 fara punct sa in strategii simple, strategiile optime si valoarea jocului sunt urmatoarele:

unde

intr-un joc matricial 2x1 fara punct sa in strategii simple, strategiile optime si valoarea jocului sunt date de:

Rezultatul general insa este prezentat in cele ce urmeaza sub forma a doua metode de determinare (exacta si aproximativa) a punctelor sa.

Fie jocul matricial caracterizat de matricea A :

unde

iar multimile strategiilor simple ale celor doi jucatori sunt:

In aceste conditii valoarea jocului este marimea:

(si se demonstreaza ca este unica), unde sunt strategii mixte ale celor doi jucatori si in acelasi timp puncte echilibru.

Suportul teoretic pentru rezolvarea unui joc matricial este urmatorul:

Teorema 2

Rezolvarea unui joc matricial in strategii mixte cu matricea este echivalenta cu rezolvarea cuplului de probleme de programare liniara duala:

Valoare jocului este:

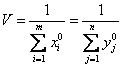
unde sunt solutiile optime ale celor doua probleme.

Strategiile optime sunt date de :

Exemplu

Sa presupunem ca primul decident adopta numai strategii simple iar cel de-al doilea numai strategii mixte:

Fie valoarea medie a jocului, unde este o strategie mixta a primului jucator,

Prima conditie ca valoarea medie a jocului sa fie cat mai mare, suntem condusi la problema:

Vom nota si problema anterioara devine:

Punand conditia ca M sa fie maxim suntem condusi la urmatoarea problema de programare liniara: