Practica controlului statistic al proceselor de fabricatie

Practica controlului statistic al proceselor de fabricatie

1. Limitele de control si de supraveghere

2. Controlul statistic prin masurare

3. Controlul statistic prin atribuire

4. Controlul prin numar de defecte

1. Limitele de control si de supraveghere

Controlul statistic al proceselor de fabricatie consta in prelevarea, la intervale de timp determinate, a unor esantioane compuse dintr-un numar de unitati, dinainte stabilit, pe baza carora se calculeaza estimatiile parametrilor care caracterizeaza reglarea sau precizia masinii.

Esantioanele prelevate fiind o parte din productie, rezulta ca valorile parametrilor de calitate ce se calculeaza cu aceste probe au o abatere negativa sau pozitiva fata de valoarea reala. Deci se va obtine o anumita eroare cunoscuta sub denumirea de eroare de reprezentativitate. Cu o anumita probabilitate folosind metodele statisticii matematice se pot stabili pentru fiecare parametru intervalul sau de incredere sau intervalul de control. Limitele acestui interval se numesc limite de control.

In teoria controlului statistic se ia ca interval de incredere intervalul cuprins intre s

Putem scrie ca probabilitatea, ca variabila aleatoare X sa difere de parametrul centrului de grupare U, (, x_me) mai mult cu s este data de relatia:

P(|U-X|>3s F s

Limitele de control sunt valorile LCI si LCS stabilite astfel incat sa rezulte:

P(LCI£U£LCS)=1-a

daca procesul de productie se desfasoara normal si

P(LCI£U£LCS)=b

daca procesul de productie nu se desfasoara normal. In practica pentru a marii siguranta in conducerea procesului de productie se lucreaza cu limite de control care nu respecta regula 3s. Se folosesc uneori valorile 2s s sau altele intermediare; ex. 1,96s, ceea ce corespunde unui risc de genul I, de 5%. Limitele intervalului de incredere pentru a=5% poarta denumirea de limite de supraveghere (LSI, LSS).

In fig 1 se prezinta legatura dintre toleranta, control si supraveghere.

Controlul statistic al desfasurarii procesului de productie are la baza ipoteza ca marea majoritate a caracteristicilor de calitate sunt variabile aleatoare care urmeaza o lege de repartitie normala sau aproximativ normala, cu media m si dispersia s

In functie de modul de exprimare al caracteristicii de calitate, se folosesc:

-controlul prin masurare;

-controlul prin atribute;

-controlul prin numar de defecte.

2. Controlul statistic prin masurare.

Se foloseste pentru acele caracteristici de calitate ale produselor care se pot exprima numeric si masura cu ajutorul aparatelor universale.

Fie X caracteristica de calitate supusa controlului si x_i valoarea fiecarei probe valorificate din cele n care alcatuiesc esantionul prelevat. Notam cu m si s media si abaterea medie patratica ale caracteristicii de calitate in momentul realizarii controlului, iar cu m_o si s_o valorile prevazute in specificatii. Controlul statistic are la baza ipoteza H_O: m=m_o; s s_o pentru proces sub control, cu alternativa H_o: m¹m_o; s¹s_o pentru procesele iesite de sub control.

Pentru controlul prin masurare se folosesc:

-metode pentru controlul reglarii:

-metoda mediei aritmetice;

-metoda medianei.

-metode pentru controlul preciziei:

-metoda abaterii mediei patratice;

-metoda amplitudinii.

2.1. Metoda mediei aritmetice

Pentru controlul statistic al caracteristicii calitative X se foloseste in acest caz drept parametru pentru caracterizarea reglarii media aritmetica a probei.

Ipoteza nula care se testeaza este:

H₀:m=m₀, cu alternativa H₀:m¹m₀

Parametrul m se estimeaza cu ajutorul mediei aritmetice a probei , calculata cu valorile x₁, x₂, , x_n luate periodic din productia masinii.

Eoarece valorile caracteristicii studiate X pot fi privite ca variabile aleatoare si extractiile independente, se poate afirma ca media probei se repartizeaza, cand marimea probei este mare, aproximativ normal cu media M()=m si dispersia

In ipoteza ca valorile caracteristicii se repartizeaza normal, calculul limitelor de control se efectuiaza diferit tinand seama daca:

a. se cunoaste abaterea medie patratica a populatiei s

b. se cunosc abaterile mediei patratice (empirice) ale mai multor esantioane:

c. se cunosc amplitudinile imprastierii mai multor esantioane.

a. Cazul cand se cunoaste abaterea medie patratica s. Pentru ca produsele obtinute sa fie corespunzatoare, masina trebuie reglata astfel incat centrul de reglare (centrul campului de imprastiere, adica valoarea medie ) sa coincida cu centrul campului de toleranta TC.

Limitele de control se determina pornind de la riscul de genul I, a dat de relatia:

a=1-P[LCI££LCS]=1-P[ |-TC|£ L

unde P[LCI££LCS] este probabilitatea ca media esantioanelor sa aiba valorile cuprinse intre limitele de control si este reprezentata de suprafata nehasurata de sub curba in fig. 2, unde s-a notat cu L -distanta de la centru campului de toleranta la limitele de control.

L=LCS-TC=|LCI-TC|

Daca se impart expresiile -TC si L cu , rezulta:

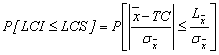
Marimea reprezinta abaterea normata a mediilor esantioanelor fata de centrul campului de toleranta TC, iar:

este abaterea normala corespunzatoare valorilor : =LCS si =LCI, determinate astfel incat riscul de genul I sa fie a, adica sa avem:

Daca mediile esantioanelor se repartizeaza dupa o lege normala, avem:

sau

Daca in relatia de mai sus se inlocuieste centrul campului de toleranta TC cu valoarea m₀, rezulta ca pentru testarea ipotezei H₀:m=m₀ se utilizeaza testul z bilateral simetric bazat pe media probei adica

Cele doua limite de control se vor realiza cu relatia

si

unde

Valorile coeficientului A in functie de a, z si n se dau in tabel.

Limitele de supraveghere pentru metoda mediei aritmetice sunt

si

Aplicatia nr. 1

In vederea introducerii controlului statistic la operatia de strunjire a unei bare metalice de la un diametru de 40 mm la 32 mm ,in cadrul analizei preliminare, au fost controlate 150 piese, obtinandu-se , s

Se cere sa se stabileasca: fractiunea defectiva si limitele de control cand se cunosc: riscul a=0,002 si marimea unei probe n=5.

Fractiunea defectiva probabila este

P=1-2F(z)=1-2F

Corespunzator unui risc de a=0,002 si unei marimi de probe de n=5, limitele de control sunt:

si

b. Cazul cand se cunosc abaterile medii patratice (empirice) ale mai multor esantioane.

Fie n esantioane pentru care se cunosc valorile mediilor patratice. Media patratica a celor n valori ale mediilor patratice va fi 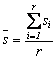, daca esantioanele au acelasi volum si daca esantioanele au volume diferite.

Determinarea limitelor de calcul are la baza relatia: ,

unde b_n=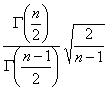 (valorile lui b_n sunt date de tabelele din STAS R5880-72).

Fractiunea defectiva se calculeaza cu relatia:

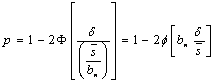
Se recomanda utilizarea acestei metode cand procesul tehnologic permite numai cercetarea loturilor de volum redus.

Limitele de control sunt:

LCI=TC - z_a si LCS=TC + z_a

c. Cand se cunosc amplitudinile imprastierii mai multor esantioane.

Fie n esantioane pentru care se cunosc amplitudinile de imprastiere R_i=x_imax-x_imin. Amplitudinea medie a esantioanelor este:

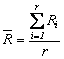, sau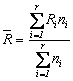

La stabilirea limitelor de control se pleaca de la relatia:

unde a_n este valoarea medie a variabilei   data in tabelul urmator.

Aceasta metoda se recomanda sa se utilizeze cand natura procesului de productie nu permite cercetarea unui lot mai mare de produse si, ca urmare, caracterizarea preciziei masinii se face pe baza esantioanelor de volum redus. Relatiile de calcul al limitelor de control sunt:

LCI=TC- si LCS=TC+

Aplicatia nr. 2

Se propune introducerea controlului statistic pentru operatia de cantarire a pchetelor de unt, inainte de ambalare, care trebuie sa aiba 200 grame. In urma analizei efectuate asupra unui numar de 100 pachete a rezultat ca aceasta caracteristica se repartizeaza normal cu media , si abaterea medie patratica s

Se cere:

-daca se poate introduce controlul statisti, cand se da ca fractiunea defectiva trebuie sa aiba valoarea cel mult 2%;

-sa se determine limitele de control, cand se cunosc : riscul de genul I, a=2%, n=5, n=10 ;

-sa se stabileasca limitele de supraveghere pentru a=5%, n=5, n=10

P=1-2F(z)=1-2F()=1-2F

Intrucat fractiunea defectiva p este mai mica de 2%, se poate introduce controlul statistic

In continuare se determina limitele de control. Pentru aceasta trebuie sa ne stabilim valoarea lui z_a. Putem considera riscul de genul I_(a egal cu fractiunea defectiva p sau egala cu 2 Se considera a=2. In acest caz z_a=3,09 rezultand ca:

si

In ncazul cand consideram valoarea riscului de genul I egala cu valoarea fractiunii defective specifice procesului, adica a=p=0,0032, iar z_a=2,941, vom obtine urmatoarele limite de control pentru medie:

si

Limitele de supraveghere se vor determina pentru a=0,05, caruia ii corespunde valoarea z_a=1,96, adica:

si

2.2. Metoda medianei

Deoarece mediana se obtine usor, aceasta metoda este des utilizata.

Pentru n suficient de mare, mediana se repartizeaza normal cu media:

si cu abaterea medie patratica:

Rezulta ca imprastierea medianelor este mai mare decat imprastierea mediilor aritmetice ale esantioanelor si ca urmare, mediana conduce la o estimare mai putin precisa a reglajului procesului decat media aritmetica.

Ca si la medie, calculul limitelor de control pentru mediana se efectueaza diferit, dupa cum urmeaza:

1. se cunoaste abaterea medie patratica, limitele de control si de supraveghere se calculeaza cu relatiile:

-limitele de control:

si

Valorile coeficientului se dau tabelar

-limitele de supraveghere:

si

Daca fractiunea defectiva este p>0,02, controlul se introduce numai in mod experimental ca in cazul metodei mediei aritmetice. Limitele de control se calculeaza in acest caz cu relatiile:

Valorile coeficientului D se prezinta in tabelul urmator:

1. se cunosc abaterile medii patratice ale mai multor esantioane, Limitele de control se calculeaza cu relatiile:

si

3. se cunosc amplitudinile mai multor esantioane, limitele de control se calculeaza cu relatiile:

si

Valorile coeficientului E sunt date tabelar

Aplicatinr. 3

Pentru aplicatia nr1 sa se stabileasca LCI si LCS

2.3. Metoda abaterii medii patratice

Abaterea medie patratica este un parametru care caracterizeaza precizia masinii, in acest caz se testeaza ipoteza:

H₀:s s , pentru precizie corespunzatoare, cu alternativa:

H₀:s¹s , pentru precizie necorespunzatoare.

Cat timp procesul se desfasoara cu precizia care-i este caracteristica, abaterea medie patratica ramane neschimbata. In asemenea situatii abaterea medii patratice ale probelor nu depasesc o valoare bine determinata, denumita prag critic s_p, sau limita de control superioara LC(s

Probabilitatea ca abaterile medii patratice ale probelor sa depaseasca limita de control este:

a=P(s)>LC(s

Cunoscand ca marimea urmeaza legea de repartitie c cu n-1 grade de libertate, se poate scrie relatia de mai sus sub forma:

unde p=1-a/2, Intrucat nu intereseaza numai limita de control superioara

In acest caz rezulta ca limita de control este:

sau LC(s sF

unde:

Limita de supraveghere se calculeaza cu relatia:

unde .

Valorile lui F se dau tabelar.

Daca nu se cunoaste abaterea medie patratica din cercetarile anterioare pentru un proces de fabricatie sau daca fractiunea defectiva p>0,02 limita de control se calculeaza astfel:

si a=p=0,02, adica:

In cazul in care abaterea medie patratica a caracteristicii de calitate nu este cunoscuta, insa se dispunem de amplitudinea medie , limita de control este:

sau

unde , iar valorile lui G se dau tabelar.

Controlul se realizeaza astfel:

-se calculeaza, pentru fiecare proba, abaterea medie patratica a probei s, care se compara cu limita de control, intalnindu-se trei situatii:

-s£LS(s), caz in care procesul se considera corespunzator ca precizie si se continua;

-s>LC(s), caz in care procesul nu corespunde ca precizie, se opreste, se depisteaza si se inlatura cauza care a perturbat procesul;

-LS(s)<s£LC(s), caz de atentionare ca asupra procesului poate interveni o cauza sistemica care sa duca la inrautatirea preciziei.

Aplicatia nr. 4

Se propune introducerea controlului statistic pentru verificarea caracteristicii calitative marimea diametrului strunjit F . In urma analizei efectuate asupra unui numar de 150 de bucati a rezultat ca aceasta caracteristica se repartizeaza normal cu media =30,1 si abaterea medie patratica s=0,126 si fractiunea defectiva p=0.002 Volumul probei de control il vom stabili la 7 bucati

Avand abaterea medie patratica s=0,126 si p=0.002 rezulta:

Deoarece c =

2.4. Metoda amplitudinii imprastierii

Amplitudinea imprastierii R este un parametru al preciziei masinii si in practica se utilizeaza adesea in locul abaterii medii patratice. Ca si in cazul abaterii medii patratice, nu se calculeaza decat limita superioara de control a amplitudinii esantionului.

In intervalul de timp cat precizia masinii este normala, valorile amplitudinii imprastierii, determinata prin controlul efectuat asupra esantioanelor prelevate, nu depasesc o anumita valoare R₀ ce se stabileste astfel incat probabilitatea depasirii ei sa fie a£0,05. Valoarea astfel gasita se numeste limita de control si se noteaza LC( R).

Deoarece riscul de genul I este dat de relatia:

unde t_a este valoarea raportului R₀/s, corespunzatoare riscului a/2, rezulta ca limita controlului pentru amplitudinea probei se calculeaza cu relatia:

Valorile sunt prezentate tabelar. Limita de supraveghere este:

Daca se cunoaste amplitudinea medie a imprastierii , limita de control se obtine cu relatia:

Valorile lui a_n se dau tabelar.

Cand nu se cunosc abaterea medie patratica si amplitudinea medie a imprastierii sau cand p>0,02, se ia s=T/6 si a=0,02. Relatia de calcul al limitei de control este:

Interpretarea rezultatelor se face asemanator ca la metoda abaterii medii patratice.